Oracle - 多区间按权重取值逻辑
啰嗦: 其实很早就遇到过类似问题,也设想过,不过一致没实际业务需求,也就耽搁了;最近有业务提到了,和同事讨论,各有想法,所以先把逻辑整理出来,希望有更好更优的解决方案;
背景:
某业务配置表,按配置的时间区间及组织层级取方案,形成报表展示出所有部门方案的取值;
例如,总公司配置20230101-20231231为方案3, 分公司配置 20230301-20230731 为方案2,部门配置20230601-20231031 为方案1,配置优先级为 部门> 分公司>总公司 ,即啥都没配则使用总公司默认值;

分析: 如果是单天计算, 那很简单,可以直接按天匹配,然后取 方案1> 方案2> 方案3;
现在要展示,讨论有2种方案,1.区间完全切割开,形成最小时间区间,进行取值;2.放临时表,从低优先级开始,进行不断迭代覆盖;
这里主要展示方案1, 主要感觉方案1可以直接查询出来,应该是比较简单的;
直接贴代码
WITH A AS --基础数据(SELECT 3 AS LEVE, '20230101' AS BEGINDATE, '20231231' AS ENDDATEFROM DUALUNION ALLSELECT 2 AS LEVE, '20230301' AS BEGINDATE, '20230731' AS ENDDATEFROM DUALUNION ALLSELECT 1 AS LEVE, '20230601' AS BEGINDATE, '20231031' AS ENDDATEFROM DUAL),
B AS --开始日期和截止日期合并一列(SELECT BEGINDATE AS DAY FROM A UNION SELECT ENDDATE FROM A ORDER BY DAY),
C AS --生产日期节点前后一天,将时间边界当天天单独作为一条记录(SELECT DAY,TO_CHAR(TO_DATE(DAY, 'yyyyMMdd') - 1, 'yyyyMMdd') AS DAY_LAST,TO_CHAR(TO_DATE(DAY, 'yyyyMMdd') + 1, 'yyyyMMdd') AS DAY_NEXT,ROWNUM NFROM B),
D AS --生成最小的时间区间,并关联各个时间边界当天(SELECT C1.DAY_NEXT AS BEGINDATE, C2.DAY_LAST AS ENDDATEFROM C C1, C C2WHERE C1.N + 1 = C2.NUNIONSELECT DAY AS BEGINDATE, DAY AS ENDDATEFROM CORDER BY BEGINDATE)
--最后进行查询匹配, 权重取最小
SELECT D.*, MIN(A.LEVE) AS LEVEFROM DLEFT JOIN AON D.BEGINDATE >= A. BEGINDATEAND D.ENDDATE <= A.ENDDATEGROUP BY D.BEGINDATE, D.ENDDATEORDER BY D.BEGINDATE, D.ENDDATE执行结果 :

PS: 由于时间区间边界当天,不好判断,只能单独拉出来作为一条记录, 虽然保证了边界数据的准确性,但拆分太散后 无法合并到一起,
方便的话,告知下合并的方式,再此特别感谢。
相关文章:

Oracle - 多区间按权重取值逻辑
啰嗦: 其实很早就遇到过类似问题,也设想过,不过一致没实际业务需求,也就耽搁了;最近有业务提到了,和同事讨论,各有想法,所以先把逻辑整理出来,希望有更好更优的解决方案;…...
)
本次CTF·泰山杯网络安全的基础知识部分(二)
简记23年九月参加的泰山杯网络安全的部分基础知识的题目,随时补充 15(多选)网络安全管理工作必须坚持“谁主管、谁负责,谁运营、谁负责,谁使用、谁负责”的原则,和“属地管理”的原则 谁主管、谁负责&…...

MyBatis 映射文件(Mapper XML):配置与使用
MyBatis 映射文件(Mapper XML):配置与使用 MyBatis是一个强大的Java持久化框架,它允许您将SQL查询、插入、更新和删除等操作与Java方法进行映射。这种映射是通过MyBatis的映射文件,通常称为Mapper XML文件来实现的。本…...
基于 SpringBoot 的大学生租房网站
文章目录 1 简介2 技术栈3 需求分析4 系统设计5 系统详细设计5.1系统功能模块5.2管理员模块5.3房主功能模块5.4用户功能模块 源码咨询 1 简介 本大学生租房系统使用简洁的框架结构,专门用于用户浏览首页,房屋信息,房屋评价,公告资…...
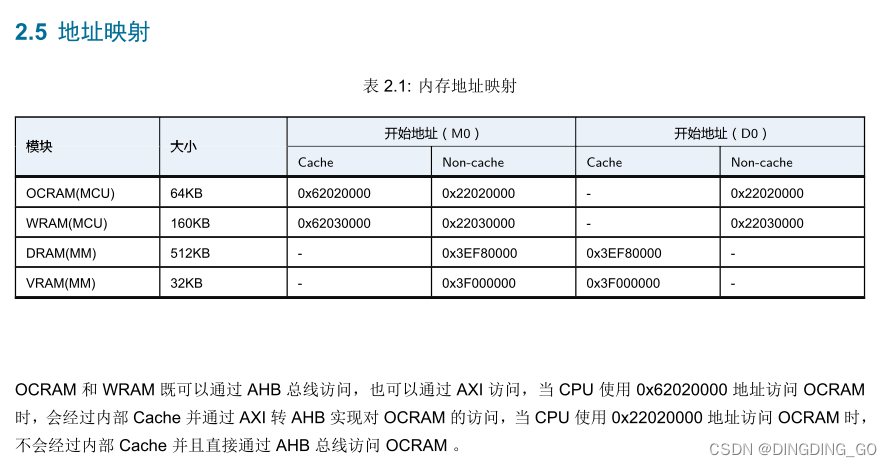
BL808学习日志-0-概念理解
一、主核心的介绍 1.三个核心在FREERTOS系统中相互独立,各负责各自的外设和程序;其中M0和LP核心在一个总线上,D0单独在一个总线上,两个总线使用AXI4.0(??)通讯? CPU0(M0)-E907架构,320MHz; CPU1(LP)-E9…...

CISSP学习笔记:业务连续性计划
第三章 业务连续性计划 3.1 业务连续性计划 业务连续性计划(BCP): 对组织各种过程的风险评估,发生风险的情况下为了使风险对组织的影响降至最小而定制的各种计划BCP和DRP首先考虑的人不受伤害,然后再解决IT恢复和还原问题BCP的主要步骤: 项…...

.NET Nuget包推荐安装
文章目录 前言通用WPFWebApiBlazor 前言 我这里的包主要是.NET Core的,.NET Framework可能不支持。 通用 Newtonsoft.Json:最常用的C#和Json对象互转的包。支持匿名对象,但是不支持Enum枚举类型,显示的是Enum的数值,…...
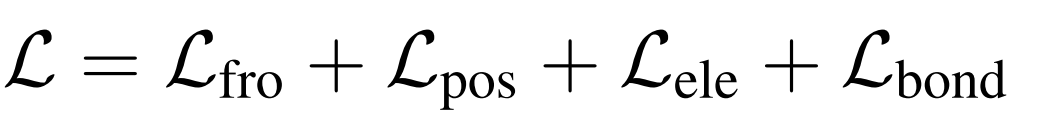
【文献阅读】Pocket2Mol : 基于3D蛋白质口袋的高效分子采样 + CrossDocked数据集说明
Pocket2Mol: Efficient Molecular Sampling Based on 3D Protein Pockets code: GitHub - pengxingang/Pocket2Mol: Pocket2Mol: Efficient Molecular Sampling Based on 3D Protein Pockets 所用数据集 与“A 3D Generative Model for Structure-Based Drug Desi…...

TrustRadius 评论:为什么 Splashtop 优于 LogMeIn
在当今日益数字化的格局中,远程访问和远程支持工具不仅方便而且至关重要。无论对于居家办公人员,还是对于提供远程支持的 IT 专家,能够安全高效地访问远程系统已成为以技术为导向的日常生活的主要内容。 Splashtop 和 LogMeIn 是远程领域的两…...
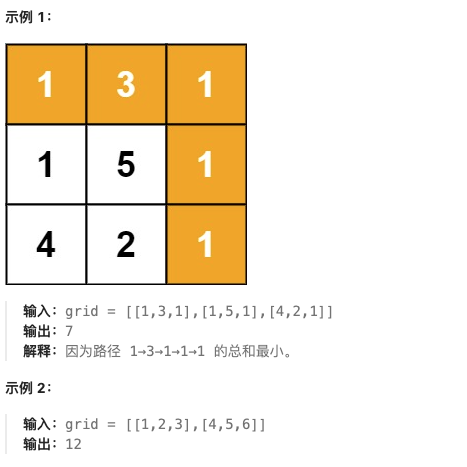
【动态规划】动态规划经典例题 力扣牛客
文章目录 跳台阶 BM63 简单跳台阶扩展 JZ71 简单打家结舍 LC198 中等打家劫舍2 LC213中等最长连续递增序列 LC674 简单乘积最大子数组LC152 中等最长递增子序列LC300 中等最长重复子数组LC718最长公共子串NC BM66最长公共子序列LC1143 中等完全平方数LC279零钱兑换 LC322 中等单…...
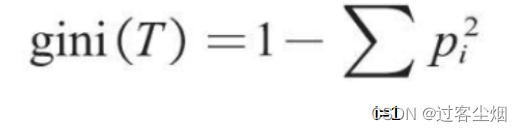
统计模型----决策树
决策树 (1)决策树是一种基本分类与回归方法。它的关键在于如何构建这样一棵树。决策树的建立过程中,使用基尼系数来评估节点的纯度和划分的效果。基尼系数是用来度量一个数据集的不确定性的指标,其数值越小表示数据集的纯度越高。…...

C# List 复制之深浅拷贝
C# List 复制 之深浅拷贝 声明类 public class TestStu{public int Number{get;set; }public string Name{get;set; }}public static async Task<int> Main(string[] args){var stu1 new TestStu(){Number 1,Name "1"};var stu2 new TestStu(){Numbe…...
)
论<script> 标签可以直接写在 HTML 文件中的哪些位置?(可以将 <script> 标签直接插入到 HTML 文件的任何位置)
可以将 <script> 标签直接插入到 HTML 文件的任何位置,以在相应位置执行 JavaScript 代码。 以下是几个示例: 1.<head> 元素内部:在 <head> 元素内部放置 <script> 标签时,脚本将在页面加载过程中被下载和…...
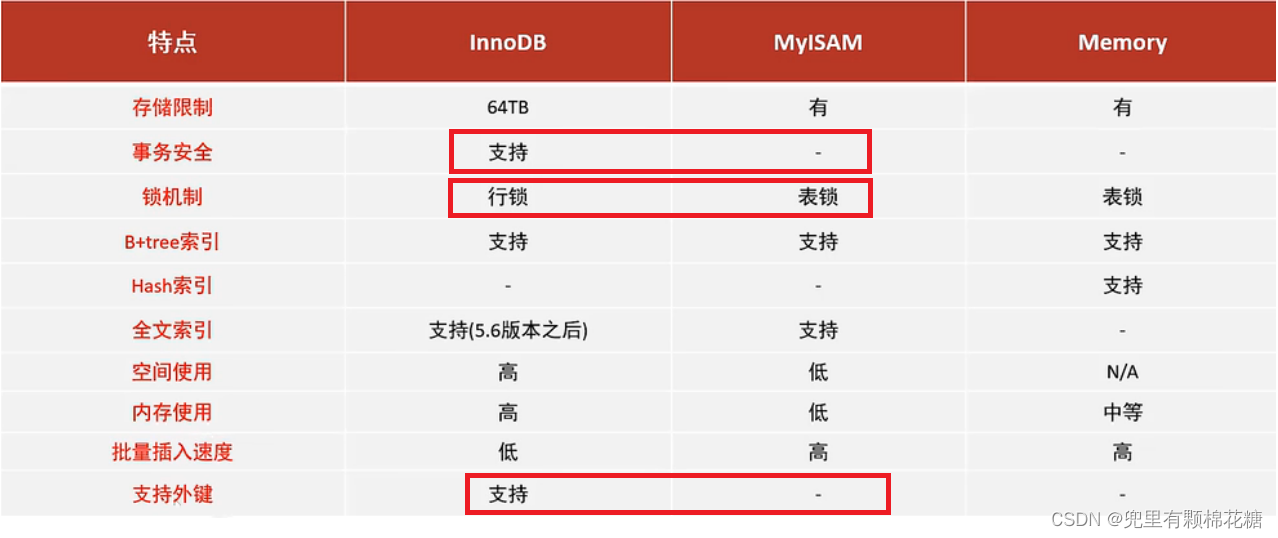
【MySQL进阶】--- 存储引擎的介绍
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【MySQL学习专栏】🎈 本专栏旨在分享学习MySQL的一点学习心得,欢迎大家在评论区讨论💌 目录 一、什么…...
self-XSS漏洞SRC挖掘
本文由掌控安全学院 - 一朵花花酱 投稿 Markdown是一种轻量级标记语言,创始人为约翰格鲁伯(John Gruber)。它允许人们使用易读易写的纯文本格式编写文档,然后转换成有效的 XHTML(或者HTML)文档。这种语言吸…...

1859. 将句子排序
目录 一、题目 二、代码 一、题目 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 二、代码 定义了一个vector<vector<string>> v(MAX);采用const string& word : v[k] word 就会依次取得 v[k] 中的每个元素(v[k][0],…...
普通学校,普通背景,普通公司,不普通总结。
作者:阿秀 InterviewGuide大厂面试真题网站:https://top.interviewguide.cn 这是阿秀的第「313」篇原创 小伙伴们大家好,我是阿秀。 可能很多人点开牛客、知乎、B站,一看帖子的标题都是"某985xxxx"、"不入流211xxx…...
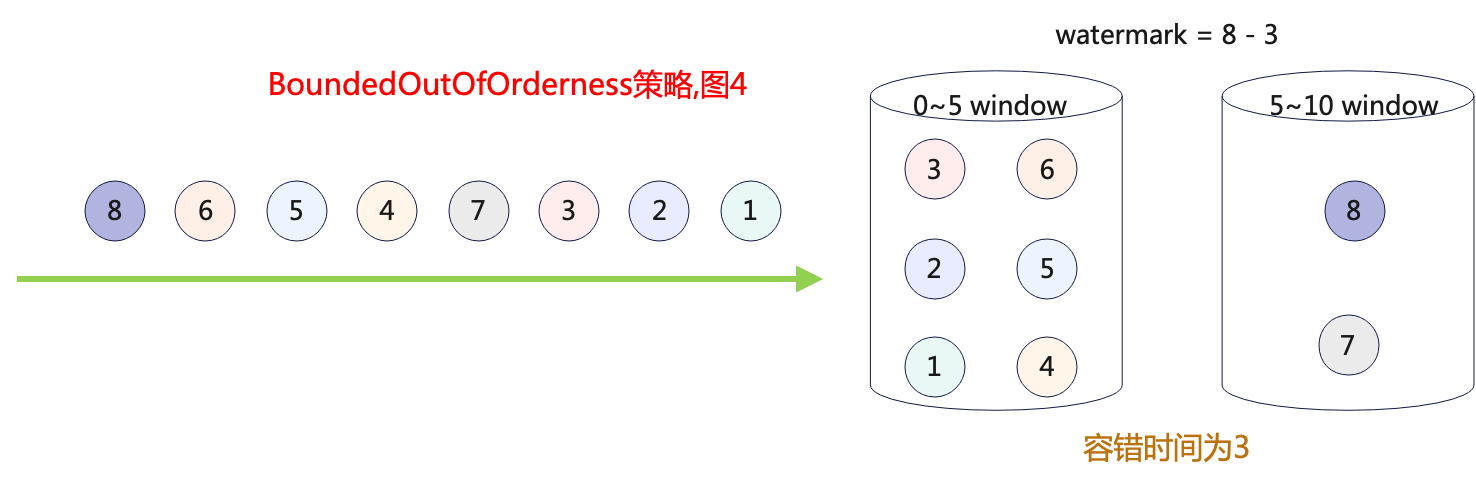
Flink之Watermark生成策略
在Flink1.12以后,watermark默认是按固定频率周期性的产生. 在Flink1.12版本以前是有两种生成策略的: AssignerWithPeriodicWatermarks周期性生成watermarkAssignerWithPunctuatedWatermarks[已过时] 按照指定标记性事件生成watermark 新版本API内置的watermark策略 单调递增的…...

提升API文档编写效率,Dash for Mac是你的不二之选
在编写和开发API文档的过程中,你是否经常遇到查找困难、管理混乱、效率低下等问题?这些都是让人头疼的问题,但现在有了Dash for Mac,一切都将变得简单而高效。 Dash for Mac是一款专为API文档编写和管理设计的工具,它…...

无人注意,新安装的 Ubuntu 23.04 不支持安装 32 位应用
导读新安装的 Ubuntu 23.04 不支持安装 32 位应用。 无人注意,新安装的 Ubuntu 23.04 不支持安装 32 位应用 有用户报告,在新安装的 Ubuntu 23.04 上从 Ubuntu 仓库安装的 Steam 客户端是不工作的。在 Ubuntu 23.04 中使用了基于 Flutter 的新安装程序…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
