gurobi属性篇一
1.构造目标函数
(1)一般的写法:
我们常见的目标函数写法通常是定义好式子z=f(x,y,...),然后用m.setObjective(z, GRB。MINIMIZE),这样的定义方式比较普遍。
这也是一般的写法。
(2)但还有一种写法,是在定义变量的时候来构造目标函数。
x = m.addVar (lb=0.0, ub=float(’inf’), obj=0.0, vtype=GRB.CONTINUOUS, name="", column=None )此处的obj是变量在目标函数中的系数。
如果obj=0,即该变量不出现在目标函数中,也是默认的形式,我们见得最多。
但如果是x=m.addVar(lb=0, float(’inf’), obj=2, vtype=GRB.CONTINUOUS),那么目标函数中会出现z=2x一项。
2.column()
这是约束中的列相关的函数。会在列生成,分支定价算法中用到。
包含:系数和变量两大类。通常是临时变量。
添加的时候用addTerm(),删除的时候用remove()。
具体如下所示:
col_coef = [1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0]
rmp_con为gurobi前期定义的一系列(24个R0,...,R24)约束# (1)列构造器,这里col_coef表示约束中的系数,rmp_con表示对应的约束,二者必须对应(维度一致)
rmp_col = Column(col_coef, rmp_con)
# <gurobi.Column: 1.0 R0 0.0 R1 1.0 R2 1.0 R3 1.0 R4 0.0 R5 0.0 R6 0.0 R7 1.0 R8
# 1.0 R9 1.0 R10 0.0 R11 1.0 R12 0.0 R13 1.0 R14 0.0 R15 1.0 R16 1.0 R17 1.0 R18
# 1.0 R19 0.0 R20 0.0 R21 0.0 R22 0.0 R23 0.0 R24 ># (2)把新列(新变量,即新产生的pattern)添加到模型中
>>>其实对应的是s = m.addVar(lb,ub,obj,vtype,name,column),其中column表示GRBColumn对象,用于指>>> 定新变量s所属的一组约束
RMP.addVar(lb = 0.0,ub = 1, obj = path_length, vtype = GRB.CONTINUOUS, name = var_name, column = rmp_col)相关文章:

gurobi属性篇一
1.构造目标函数 (1)一般的写法: 我们常见的目标函数写法通常是定义好式子zf(x,y,...),然后用m.setObjective(z, GRB。MINIMIZE),这样的定义方式比较普遍。 这也是一般的写法。 (2)但还有一种写法…...

【python数据建模】Pandas库
概述 Pandas库主要提供了三种数据结构: (1)Series:带标签的一维数据 (2)DataFrame:带标签且大小可变的二维表结构 (3)Panel:带标签且大小可变的三维数据 Pan…...
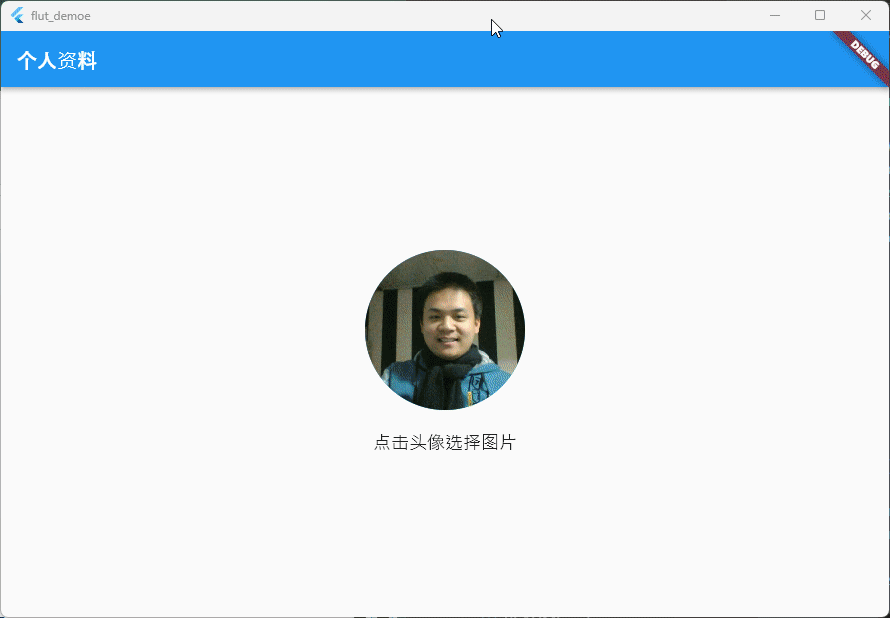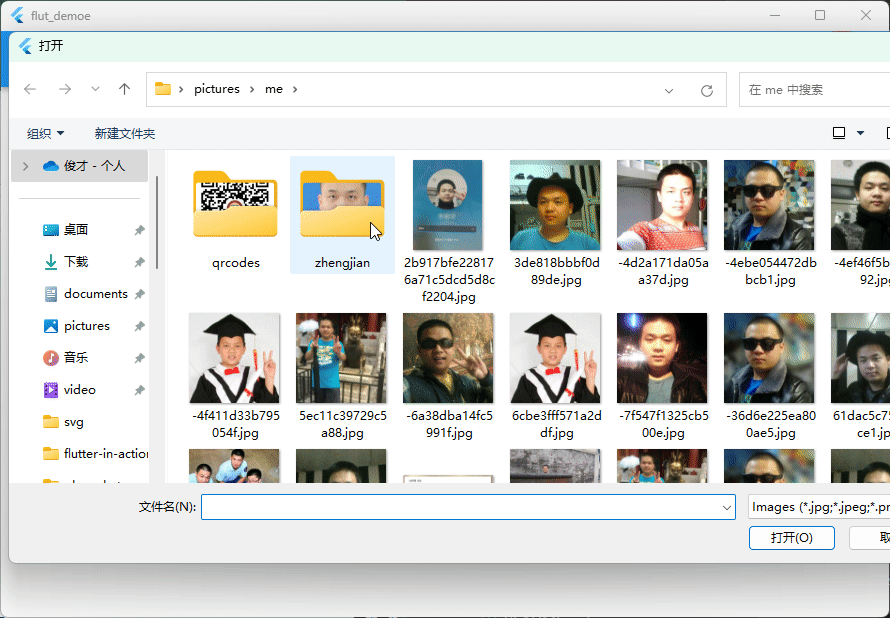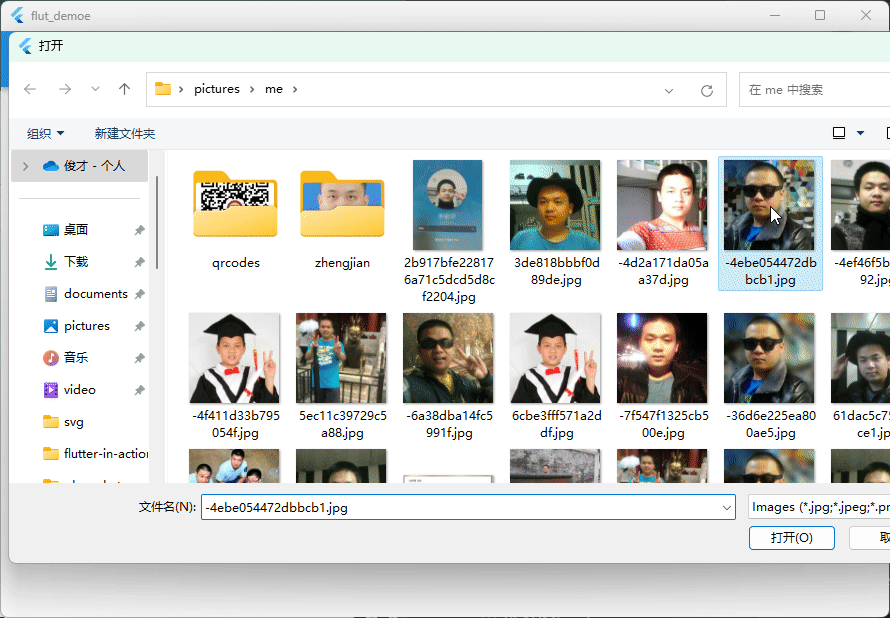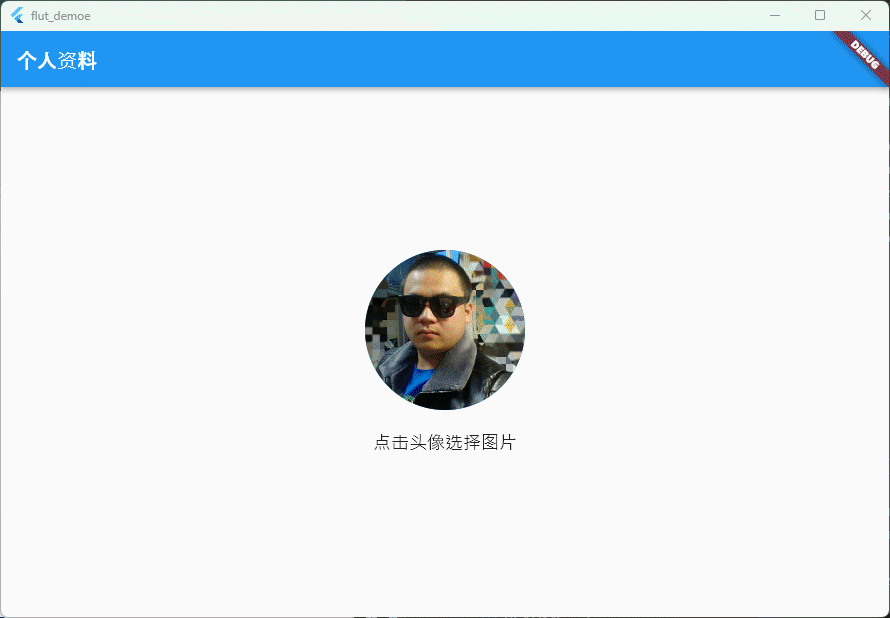
Flutter笔记:关于应用程序中提交图片作为头像
Flutter笔记 关于应用程序中提交图片作为头像 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/133418554…...
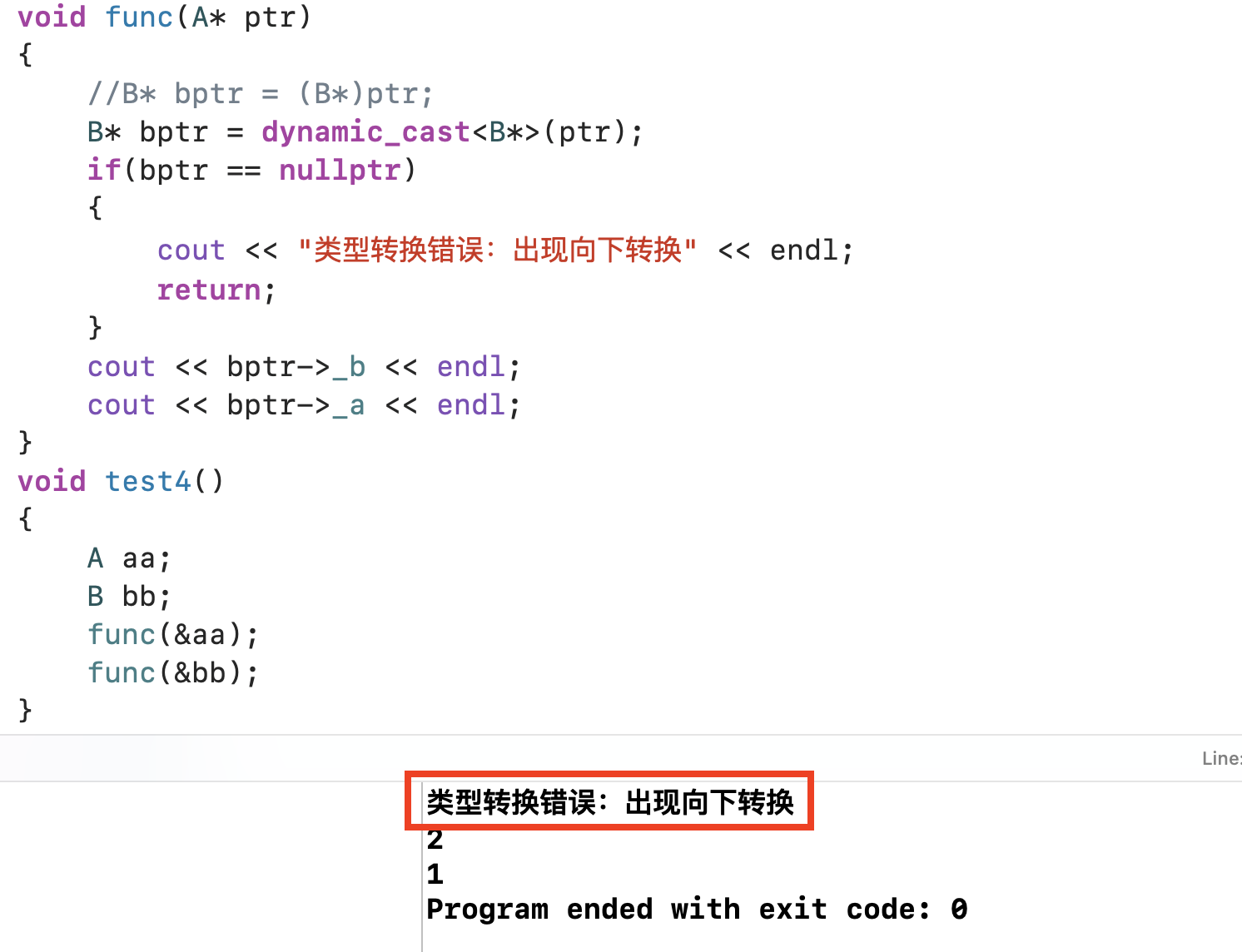
【C++】C++的类型转换
文章目录 1. C语言中的类型转换2. C中的类型转换2.1 static_cast2.2 reinterpret_cast2.3 const_cast2.4 dynamic 1. C语言中的类型转换 在C语言中,经常会出现一种情况:运算符两边的类型不同,或者形参实参类型不匹配,此时就会发生…...

ahk系列——ahk_v2实现win10任意界面ocr
前言: 不依赖外部api接口,界面简洁,翻译快速,操作简单, 有网络就能用 、还可以把ocr结果非中文翻译成中文、同样可以识别中英日韩等60多个国家语言并翻译成中文,十分的nice 1、所需环境 windows10及其以上…...

linux下端口映射
linux下端口映射 1. 允许数据包转发 echo 1 >/proc/sys/net/ipv4/ip_forwardiptables -t nat -A POSTROUTING -j MASQUERADEiptables -A FORWARD -i [内网网卡名称] -j ACCEPTiptables -t nat -A POSTROUTING -s [内网网段] -o [外网网卡名称] -j MASQUERADE# 例:…...

C++ 迭代器(iterator)
迭代器介绍 迭代器(iterator):容器类型内置的“指针” - 使用迭代器可以访问某个元素,迭代器也能从一个元素移动到另一个元素。 - 有迭代器的类型都拥有 begin 和 end 成员- begin:返回指向第一个元素(或字…...

基于Python3搭建qt开发环境
Python可视化编程相信大部分刚接触都是tkinter,tkinter是Python自带的库,不需要安装第三方库即可使用,在我的Python专栏中也有很多基于tkinter来设计的可视化界面。本篇文章将尝试另外一个Python的可视化编程库(pyqt),与tkinter编…...

Linux常见操作命令(1)
前言:作者也是初学Linux,可能总结的还不是很到位 ♈️今日夜电波:达尔文—林俊杰 0:30━━━━━━️💟──────── 4:06 🔄 ◀️ …...
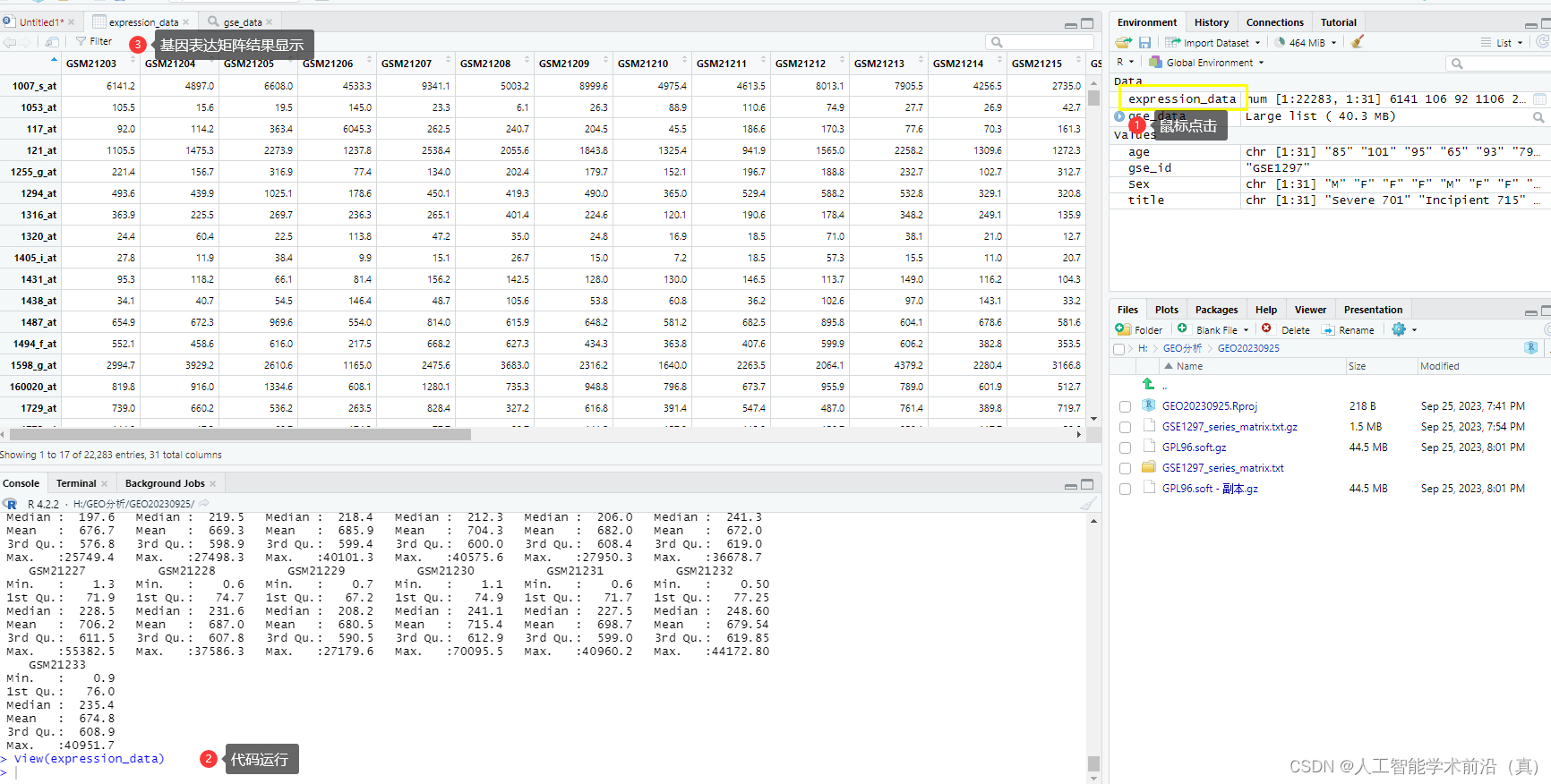
GEO生信数据挖掘(一)数据集下载和初步观察
检索到目标数据集后,开始数据挖掘,本文以阿尔兹海默症数据集GSE1297为例 目录 GEOquery 简介 安装并加载GEOquery包 getGEO函数获取数据(联网下载) 更换下载数据源 对数据集进行初步观察处理 GEOquery 简介 GEOquery是一个…...

Tensorflow2 GPU 安装方法
一、Tensorflow2 GPU 安装方法 1. 首先安装Anaconda3环境2. 在Anaconda Prompt 中安装tensorflow23. 验证GPU是否可以使用 1. 首先安装Anaconda3环境 https://www.anaconda.com/ 2. 在Anaconda Prompt 中安装tensorflow2 conda update conda conda create -n tensorflow pyt…...

QSS之QLineEdit
QLineEdit我们在开发过程中是经常使用的,一般情况下默认的风格是不适合设计师的要求,本篇介绍QLineEdit的基本qss风格: 1.基本属性设置 QLineEdit{background-color:#FFFFFF;color:#333333;border:none;} 2.悬浮状态设置 QLineEdit:hover…...
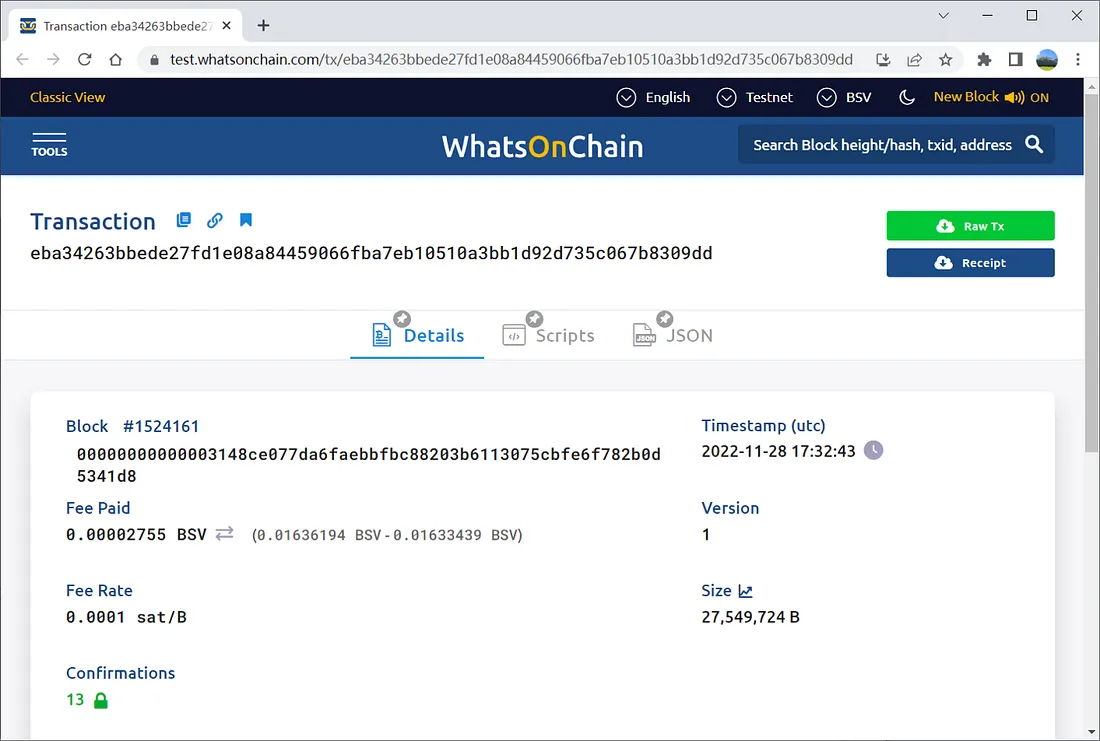
在比特币上支持椭圆曲线 BLS12–381
通过使用智能合约实现来支持任何曲线 BLS12–381 是一种较新的配对友好型椭圆曲线。 与常用的 BN-256 曲线相比,BLS12-381 的安全性明显更高,并且安全目标是 128 位。 所有其他区块链,例如 Zcash 和以太坊,都必须通过硬分叉才能升…...
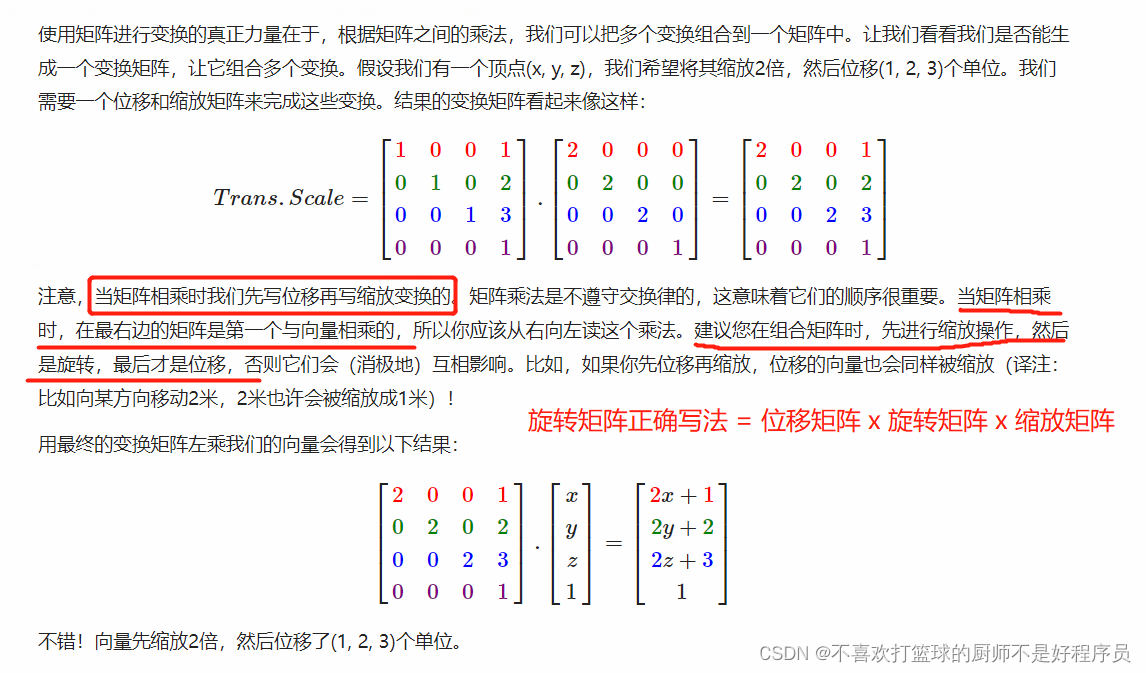
简单讲解 glm::mat4
文章目录 前言一、下载glm库二、基本数学知识1. 三维中的 4 x 4 矩阵2.旋转3. 位移4. 缩放5. 组合 三、行向量或列向量四、总结 前言 glm库是OpenGL的官方数学库,里面内置多种跟几何变换相关的函数,熟练掌握glm库可以省下很多麻烦。 因为最近在项目中主…...

第3章-指标体系与数据可视化-3.1.1-Matplotlib绘图库
目录 3.1 Python可视化 3.1.1 Matplotlib绘图库 1. 线图 2. 饼图 3. 条形图 4. 直方图 5.散点图...

探索视听新纪元: ChatGPT的最新语音和图像功能全解析
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🤖 人工智能 AI: 🧠 Machine …...
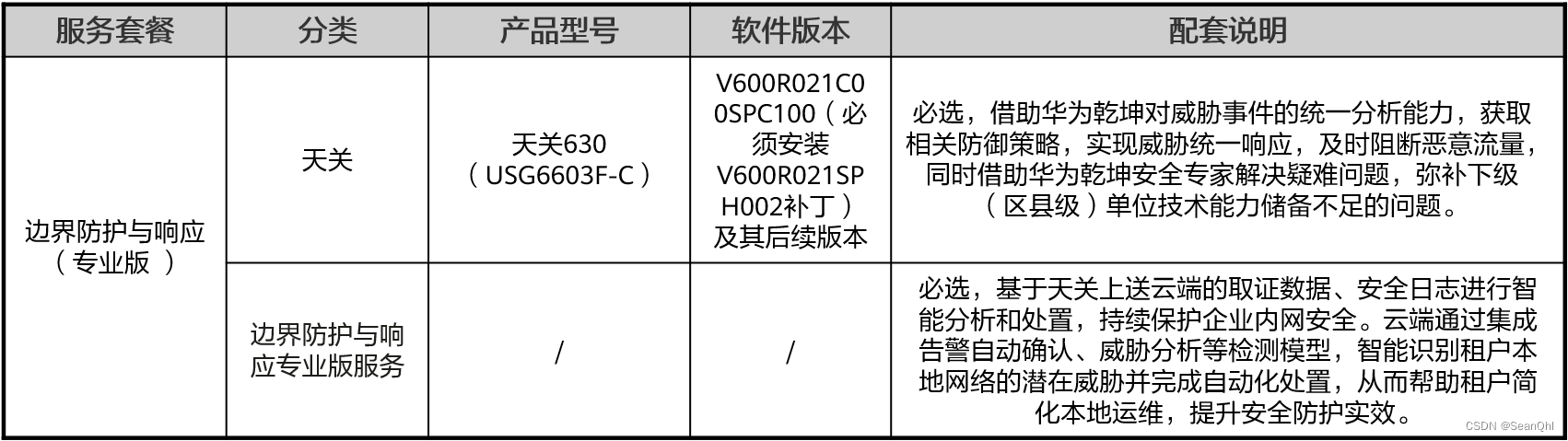
华为乾坤区县教育安全云服务解决方案(1)
华为乾坤区县教育安全云服务解决方案(1) 课程地址方案背景客户痛点分析区县教育网概述区县教育网业务概述区县教育网业务安全风险分析区县教育网安全运维现状分析区县教育网安全建设痛点分析 安全解决方案功能概述架构概述方案架构设备选型 课程地址 本…...

《Jetpack Compose从入门到实战》第三章 定制 UI 视图
目录 配置颜色、字体与形状Welcome PageLogin PageHome Page 主题CompositionLocal 配置颜色、字体与形状 -ui.theme.Color.kt val pink100 Color(0xFFFFF1F1) val pink900 Color(0xFF3F2C2C) val white Color(0xFFFFFFFF) val white850 Color(0xD9FFFFFF) val gray Col…...
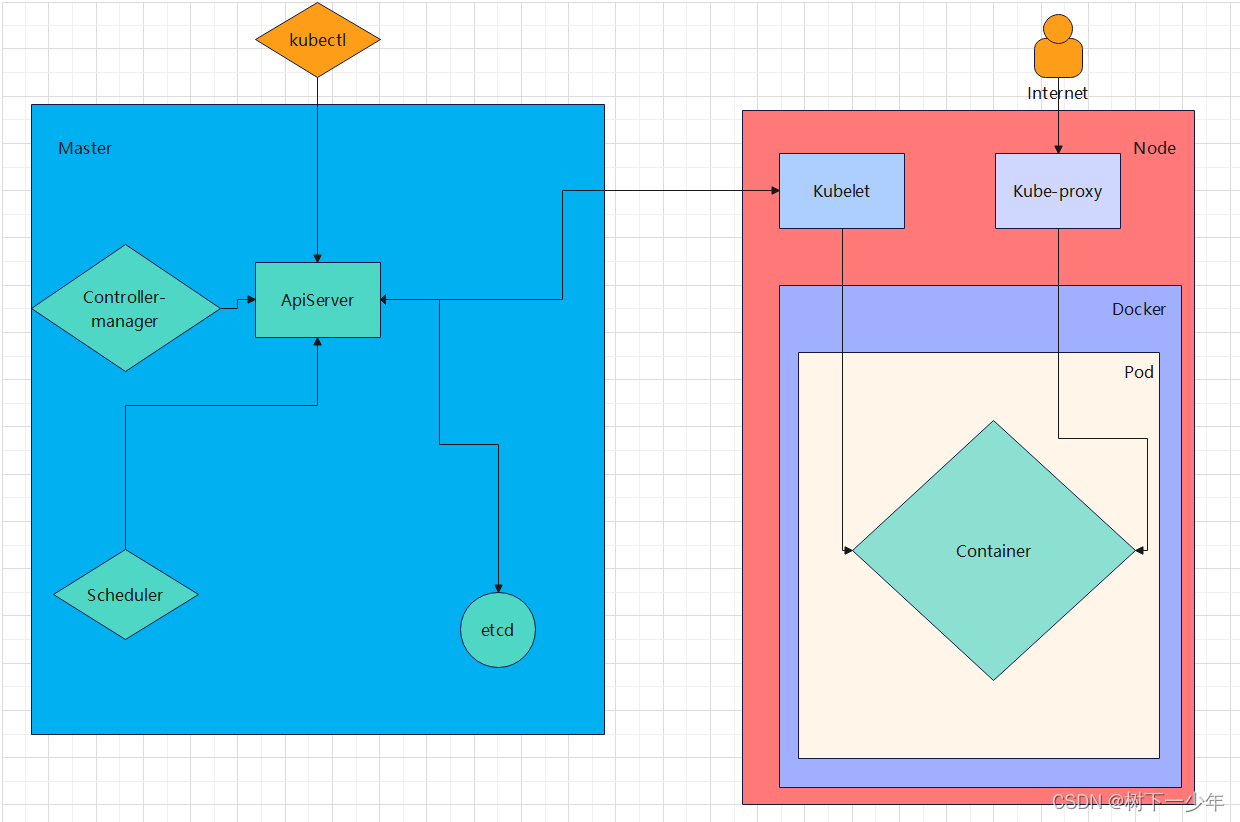
Kubernetes组件和架构简介
目录 一.概念简介 1.含义: 2.主要功能: 3.相关概念: 二.组件和架构介绍 1.master:集群的控制平面,管理集群 2.node:集群的数据平面,为容器提供工作环境 3.kubernetes简单架构图解 一.概…...
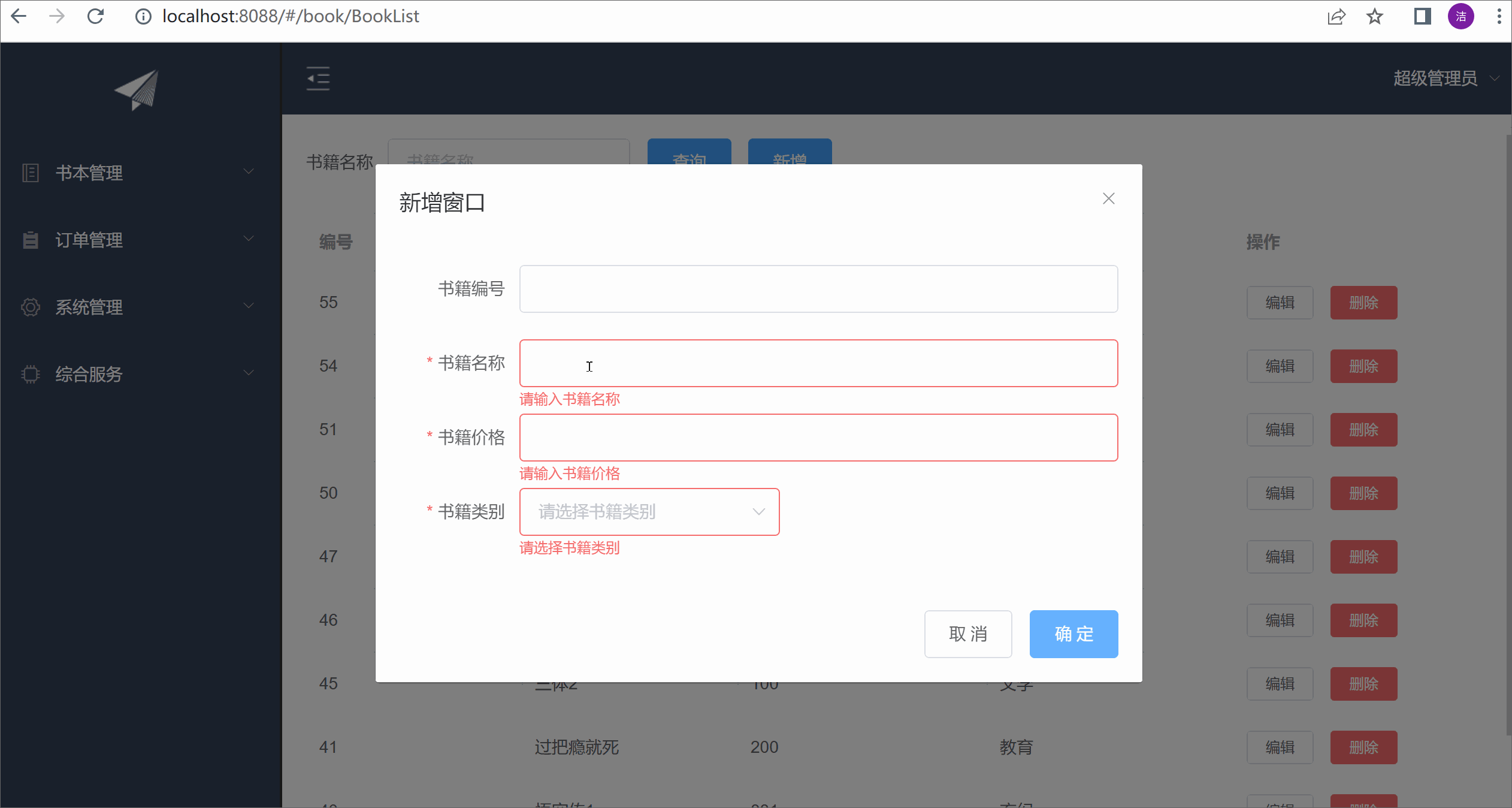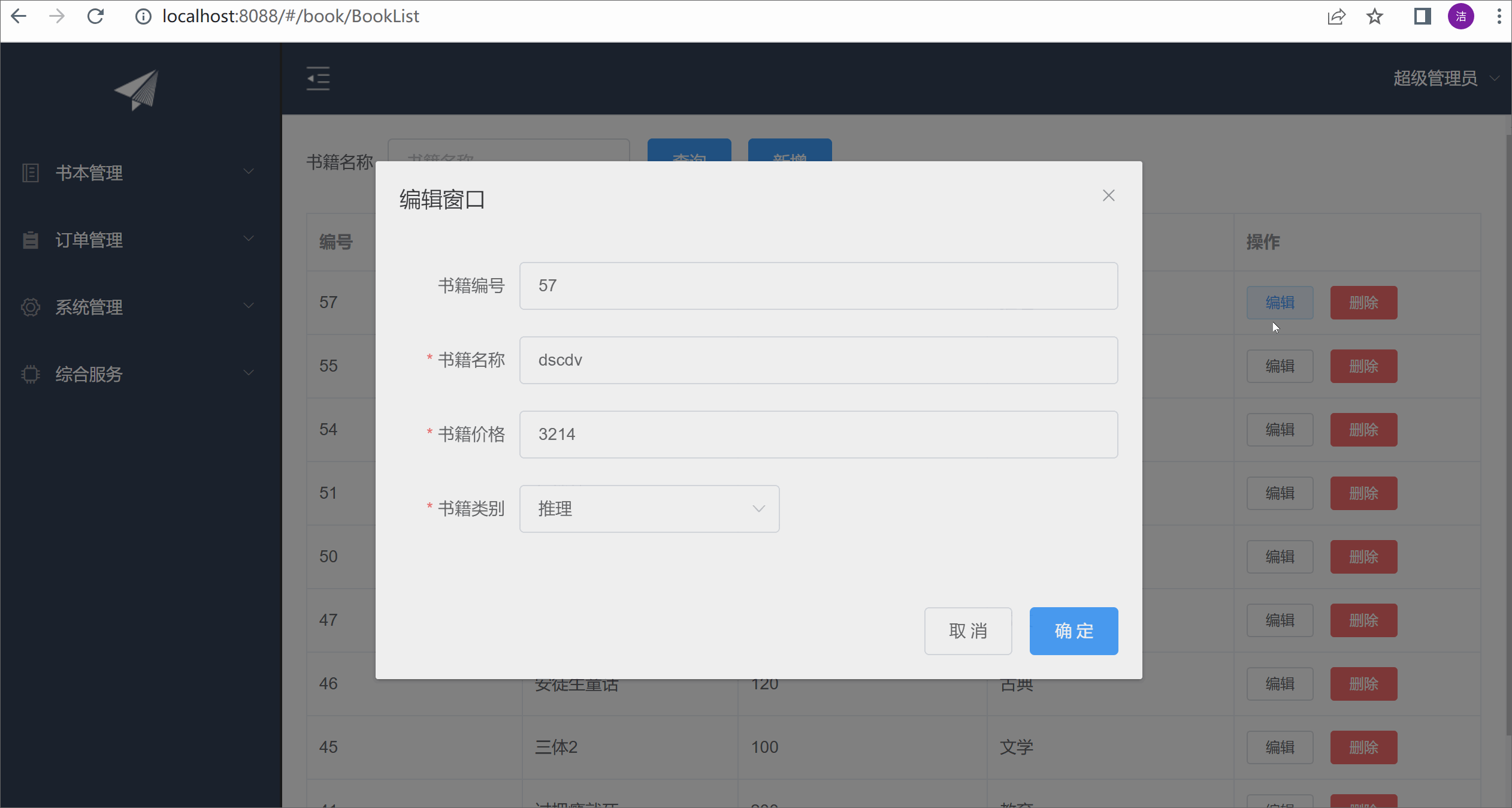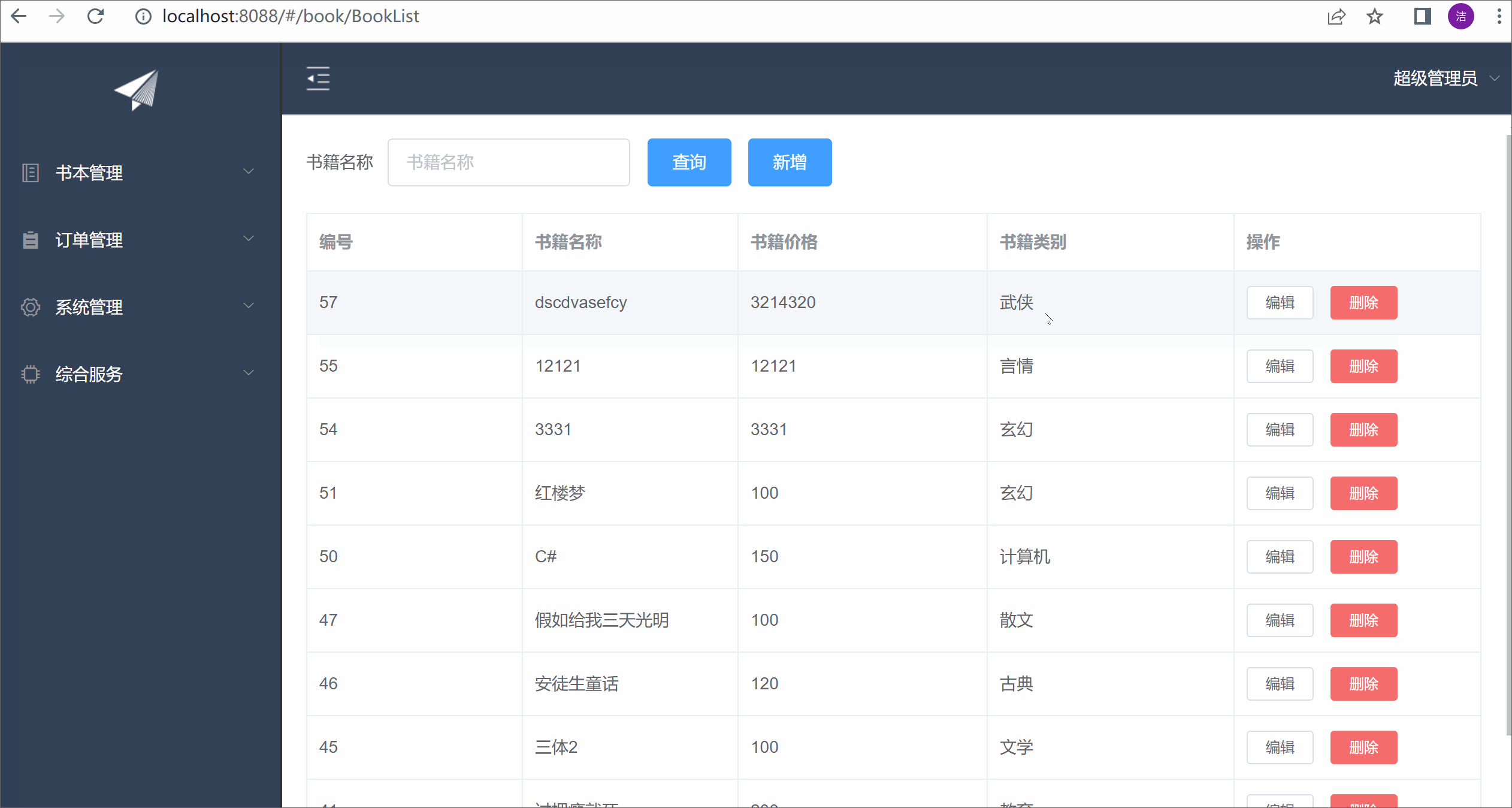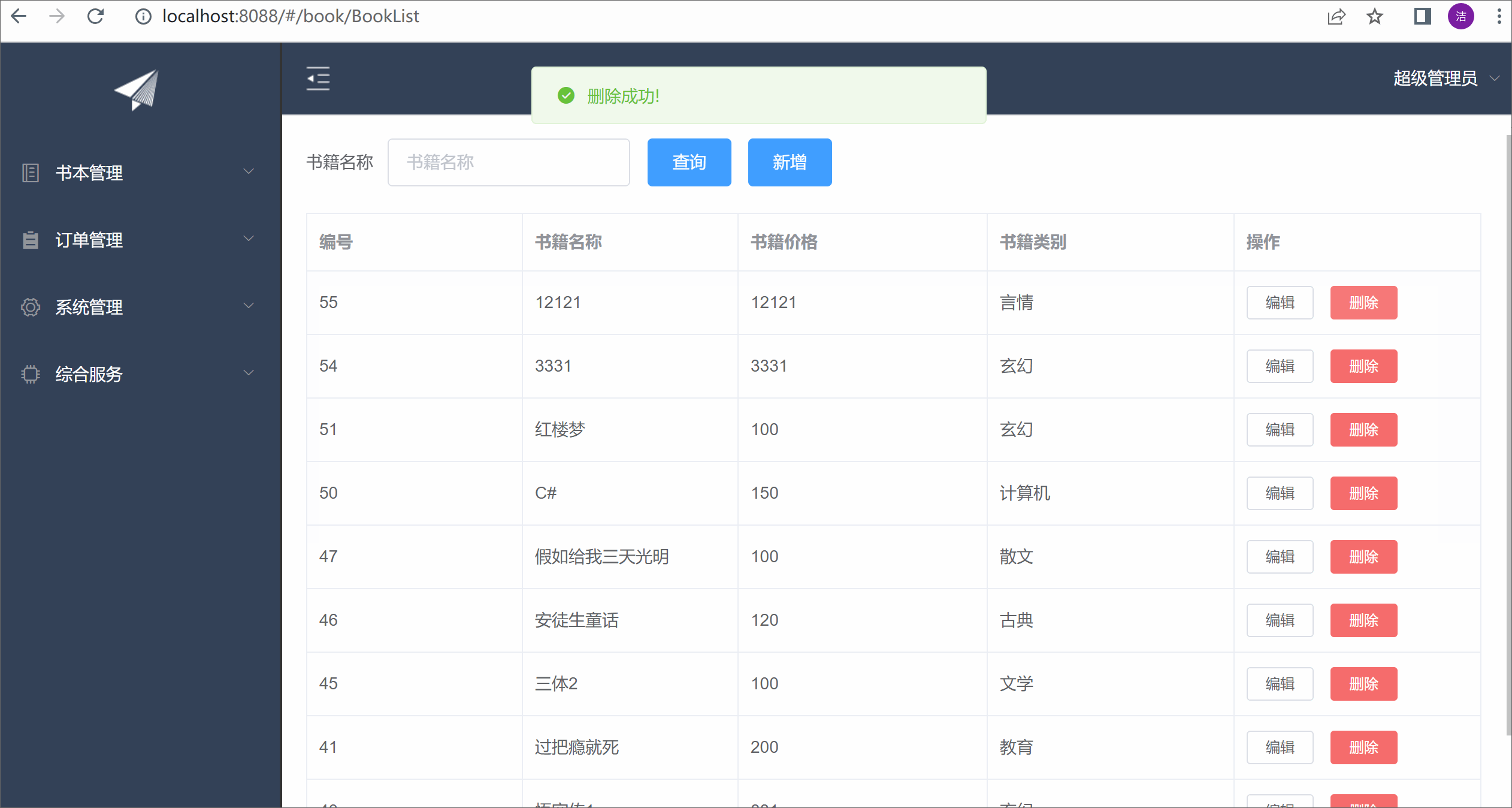
ElementUI实现增删改功能以及表单验证
目录 前言 BookList.vue action.js 展示效果 前言 本篇还是在之前的基础上,继续完善功能。上一篇完成了数据表格的查询,这一篇完善增删改,以及表单验证。 BookList.vue <template><div class"books" style"pa…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
