BI神器Power Query(25)-- 使用PQ实现表格多列转换(1/3)
实例需求:原始表格包含多列属性数据,现在需要将不同属性分列展示在不同的行中,att1、att3、att5为一组,att2、att3、att6为另一组,数据如下所示。
更新表格数据
原始数据表:
| Col1 | Col2 | Att1 | Att2 | Att3 | Att4 | Att5 | Att6 |
|---|---|---|---|---|---|---|---|
| AAA | DDD | X | O | alpha | delta | 100 | 400 |
| BBB | EEE | Y | P | beta | vega | 200 | 500 |
结果数据表:
| Col1 | Col2 | cn1 | cn3 | cn3 |
|---|---|---|---|---|
| AAA | DDD | X | alpha | 100 |
| AAA | DDD | O | delta | 400 |
| BBB | EEE | Y | beta | 200 |
| BBB | EEE | P | vega | 500 |
示例代码:
letSource = Excel.CurrentWorkbook(){[Name="Table1"]}[Content],add_index = Table.AddIndexColumn(Source, "Index", 1, 1, Int64.Type),tab1 = Table.RemoveColumns(add_index,{"Att2", "Att4", "Att6"}),rename_tab1 = Table.RenameColumns(tab1,{{"Att1", "cn1"}, {"Att3", "cn2"}, {"Att5", "cn3"}}),tab2 = Table.RemoveColumns(add_index,{"Att1", "Att3", "Att5"}),rename_tab2 = Table.RenameColumns(tab2,{{"Att2", "cn1"}, {"Att4", "cn2"}, {"Att6", "cn3"}}),combine_tab = Table.Combine({rename_tab1, rename_tab2}),sort_row = Table.Sort(combine_tab,{{"Index", Order.Ascending}}),output = Table.RemoveColumns(sort_row,{"Index"})
inoutput
代码解析:
第2行代码加载源表格,表格名称为Table1。
第3行代码添加索引列,用于确保输出结果表的数据顺序于原始表保持一致。
第4行代码移除多余列,保留部分属性列。
第5行代码重命名属性列名称。
第6~7行代码功能类似,用于提取第二组属性。
第8行代码合并两个子表。
第9行代码按索引列排序。
第1行代码移除索引列。
第12行代码输出最终结果表。
转换结果如下图所示。

部分代码也可以简化为如下,但是处理逻辑与上面代码相同,上述代码分步处理更容易理解。
letSource = Excel.CurrentWorkbook(){[Name="Table1"]}[Content],add_index = Table.AddIndexColumn(Source, "Index", 1, 1, Int64.Type),combine_tab = Table.Combine({Table.RenameColumns(add_index[[Col1],[Col2],[Att1],[Att3],[Att5],[Index]],{{"Att1","cn1"},{"Att3","cn2"},{"Att5","cn3"}}),Table.RenameColumns(add_index[[Col1],[Col2],[Att2],[Att4],[Att6],[Index]],{{"Att2","cn1"},{"Att4","cn2"},{"Att6","cn3"}})}),sort_row = Table.Sort(combine_tab,{{"Index", Order.Ascending}}),output = Table.RemoveColumns(sort_row,{"Index"})
inoutput总结:
Power Query提供了丰富的表处理功能,可以方便地实现表格列的转换需求。
相关文章:

BI神器Power Query(25)-- 使用PQ实现表格多列转换(1/3)
实例需求:原始表格包含多列属性数据,现在需要将不同属性分列展示在不同的行中,att1、att3、att5为一组,att2、att3、att6为另一组,数据如下所示。 更新表格数据 原始数据表: Col1Col2Att1Att2Att3Att4Att5Att6AAADD…...
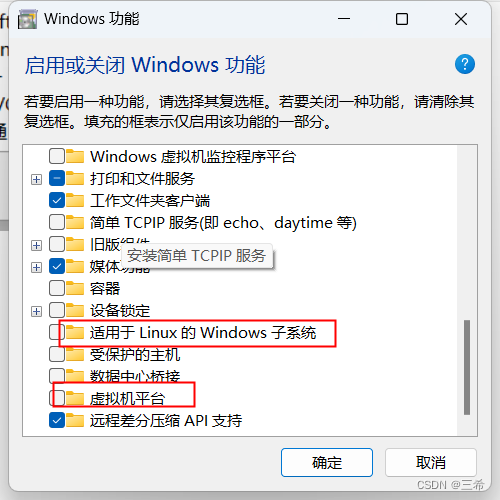
windows系统一键开启和关闭虚拟化
说明 跟虚拟化相关的三个程序 一键开启脚本 REM 开启 Hyper-V 服务 pushd "%~dp0"dir /b %SystemRoot%\servicing\Packages\*Hyper-V*.mum >hyper-v.txtfor /f %%i in (findstr /i . hyper-v.txt 2^>nul) do dism /online /norestart /add-package:"%Sy…...

NSSCTF做题(5)
[NSSCTF 2022 Spring Recruit]babyphp 代码审计 if(isset($_POST[a])&&!preg_match(/[0-9]/,$_POST[a])&&intval($_POST[a])){ if(isset($_POST[b1])&&$_POST[b2]){ if($_POST[b1]!$_POST[b2]&&md5($_POST[b1])md5($_POST[b2])){…...

java基础题——二维数组的基本应用
1.设计程序按照各个学生的 Java 成绩进行排序 ( 降序 ) 2.设计程序,根据学生总成绩进行排序(降序排列),并输出学生姓名、每门课程的名称和该学生的成绩、该学生的总成绩 public static void main(String[] args) {String[] names {"安琪拉",…...

Leetcode 2119.反转两次的数字
反转 一个整数意味着倒置它的所有位。 例如,反转 2021 得到 1202 。反转 12300 得到 321 ,不保留前导零 。 给你一个整数 num ,反转 num 得到 reversed1 ,接着反转 reversed1 得到 reversed2 。如果 reversed2 等于 num &#x…...

BI神器Power Query(27)-- 使用PQ实现表格多列转换(3/3)
实例需求:原始表格包含多列属性数据,现在需要将不同属性分列展示在不同的行中,att1、att3、att5为一组,att2、att3、att6为另一组,数据如下所示。 更新表格数据 原始数据表: Col1Col2Att1Att2Att3Att4Att5Att6AAADD…...
VUE3照本宣科——认识VUE3
VUE3照本宣科——认识VUE3 前言一、命令创建项目1.中文官网2.菜鸟教程 二、VUE3项目目录结构1.public2.src(1)assets(2)components 3. .eslintrc.cjs4. .gitignore5. .prettierrc.json6.index.html7.package.json8.README.md9.vit…...

《计算机视觉中的多视图几何》笔记(12)
12 Structure Computation 本章讲述如何在已知基本矩阵 F F F和两幅图像中若干对对应点 x ↔ x ′ x \leftrightarrow x x↔x′的情况下计算三维空间点 X X X的位置。 文章目录 12 Structure Computation12.1 Problem statement12.2 Linear triangulation methods12.3 Geomet…...

TFT LCD刷新原理及LCD时序参数总结(LCD时序,写的挺好)
cd工作原理目前不了解,日后会在博客中添加这一部分的内容。 1.LCD工作原理[1] 我对LCD的工作原理也仅仅处在了解的地步,下面基于NXP公司对LCD工作原理介绍的ppt来学习一下。 LCD(liquid crystal display,液晶显示屏) 是由液晶段阵列组成,当…...

基于Java的电影院购票系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

Linux基础指令(六)
目录 前言1. man 指令2. date 指令3. cal 指令4. bc 指令5. uname 指令结语: 前言 欢迎各位伙伴来到学习 Linux 指令的 第六天!!! 在上一篇文章 Linux基本指令(五) 中,我们通过一段故事线,带大家感性的了…...

Anderson-Darling正态性检验【重要统计工具】
Anderson-Darling正态性检验是一种用于确定数据集是否服从正态分布(也称为高斯分布或钟形曲线分布)的统计方法。它基于Anderson和Darling于1954年提出的检验统计量。该检验的基本原理和用途如下: 基本原理: 零假设(Nu…...
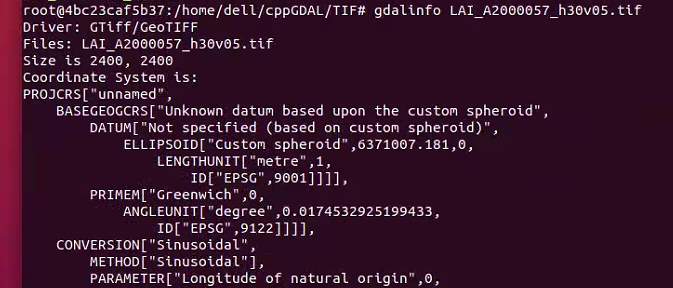
Ubuntu基于Docker快速配置GDAL的Python、C++环境
本文介绍在Linux的Ubuntu操作系统中,基于Docker快速配置Python、C等不同编程语言均可用的地理数据处理库GDAL的方法。 首先,我们访问GDAL库的Docker镜像官方网站(https://github.com/OSGeo/gdal/tree/master/docker)。其中&#x…...

<C++> 哈希表模拟实现STL_unordered_set/map
哈希表模板参数的控制 首先需要明确的是,unordered_set是K模型的容器,而unordered_map是KV模型的容器。 要想只用一份哈希表代码同时封装出K模型和KV模型的容器,我们必定要对哈希表的模板参数进行控制。 为了与原哈希表的模板参数进行区分…...

【数据结构与算法】通过双向链表和HashMap实现LRU缓存 详解
这个双向链表采用的是有伪头节点和伪尾节点的 与上一篇文章中单链表的实现不同,区别于在实例化这个链表时就初始化了的伪头节点和伪尾节点,并相互指向,在第一次添加节点时,不需要再考虑空指针指向问题了。 /*** 通过链表与HashMa…...
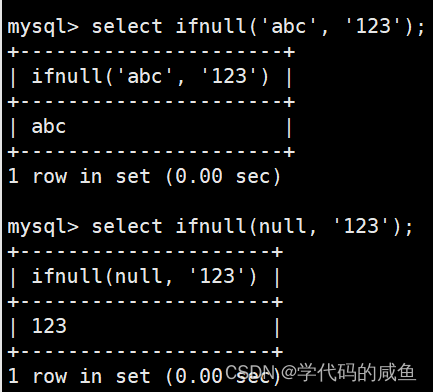
MySQL的内置函数
文章目录 1. 聚合函数2. group by子句的使用3. 日期函数4. 字符串函5. 数学函数6. 其它函数 1. 聚合函数 COUNT([DISTINCT] expr) 返回查询到的数据的数量 用SELECT COUNT(*) FROM students或者SELECT COUNT(1) FROM students也能查询总个数。 统计本次考试的数学成绩分数去…...

数据结构与算法-(7)---栈的应用-(3)表达式转换
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
)
Lilliefors正态性检验(一种非参数统计方法)
Lilliefors检验(也称为Kolmogorov-Smirnov-Lilliefors检验)是一种用于检验数据是否符合正态分布的统计检验方法,它是Kolmogorov-Smirnov检验的一种变体,专门用于小样本情况。与K-S检验不同,Lilliefors检验不需要假定数…...
)
【云原生】配置Kubernetes CronJob自动备份MySQL数据库(单机版)
文章目录 每天自动备份数据库MySQL【云原生】配置Kubernetes CronJob自动备份Clickhouse数据库 每天自动备份数据库 MySQL 引用镜像:databack/mysql-backup,使用文档:https://hub.docker.com/r/databack/mysql-backup 测试、开发环境:每天0点40分执行全库备份操作,备份文…...
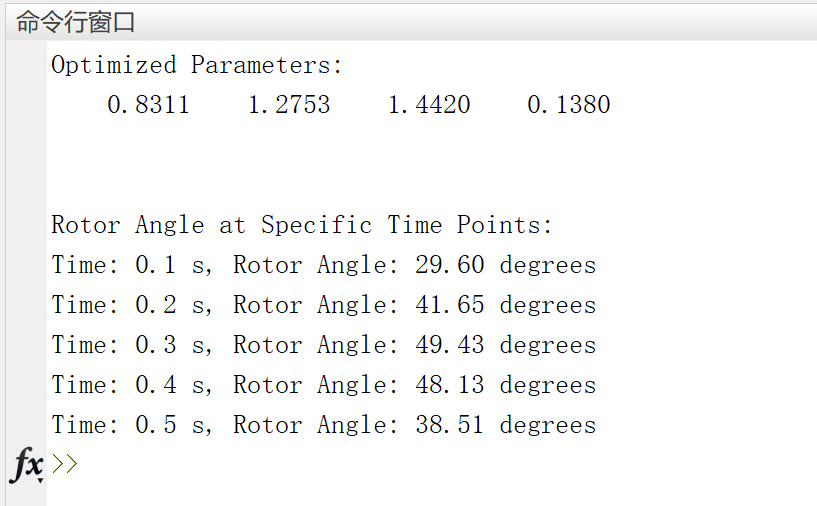
基于PSO算法的功率角摆动曲线优化研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
