Anderson-Darling正态性检验【重要统计工具】
Anderson-Darling正态性检验是一种用于确定数据集是否服从正态分布(也称为高斯分布或钟形曲线分布)的统计方法。它基于Anderson和Darling于1954年提出的检验统计量。该检验的基本原理和用途如下:
基本原理:
-
零假设(Null Hypothesis):Anderson-Darling检验的零假设是数据集来自于正态分布。这意味着,如果数据确实服从正态分布,则零假设成立。
-
计算Anderson-Darling统计量:检验首先计算Anderson-Darling统计量,这是一个衡量数据与正态分布拟合的度量。该统计量基于数据的观察值和正态分布的期望值之间的差异。
-
与临界值比较:接下来,Anderson-Darling统计量与临界值进行比较。临界值是根据所选的显著性水平(通常为5%)和数据集的大小计算得出的。如果Anderson-Darling统计量大于临界值,就意味着数据不太可能来自于正态分布。
-
做出决策:根据统计量与临界值的比较,可以决定是否拒绝零假设。如果统计量足够大,超过了临界值,通常会拒绝零假设,这意味着数据不服从正态分布。否则,不能拒绝零假设,这表示数据可能服从正态分布。
用途:
-
数据分布检查:Anderson-Darling检验可用于验证数据是否符合正态分布的假设。这对于许多统计分析和模型建立的前提非常重要,因为许多统计方法都要求数据服从正态分布。
-
质量控制:在制造业和质量控制中,Anderson-Darling检验可以用来检查生产过程是否产生了正态分布的输出。如果不是,可能需要采取措施来改进过程。
-
金融分析:在金融领域,正态分布假设经常用于分析资产价格变动。Anderson-Darling检验可以用来验证这种假设的有效性。
-
生物统计学:在生物统计学中,研究人员可能使用Anderson-Darling检验来确定生物数据是否遵循正态分布,例如基因表达数据或生物测量数据。
总之,Anderson-Darling正态性检验是一种重要的统计工具,可用于验证数据是否符合正态分布的假设,从而支持各种领域的分析和决策。
from scipy import stats
import numpy as np# 创建一个示例数据集
data = np.random.normal(0, 1, 100)# 执行Anderson-Darling正态性检验
result = stats.anderson(data)# 输出检验结果
print("Anderson-Darling统计量:", result.statistic)
print("临界值:", result.critical_values)
if result.statistic > result.critical_values[2]:print("数据不服从正态分布")
else:print("数据可能服从正态分布")print("--------------------------")
print("-检验的结果包括Anderson-Darling统计量、临界值、显著性水平以及适配结果,用于判断数据是否服从正态分布-")
print(result)
print(type(result))
print("--------------------------")
# Anderson-Darling统量
print("Anderson-Darling统计量:", result.statistic)# 临界值
print("临界值:", result.critical_values)# 显著性水平
print("显著性水平:", result.significance_level)# 适配结果
fit_result = result.fit_result
print("适配结果 params:", fit_result.params)
print("适配结果 success:", fit_result.success)
print("适配结果 message:", fit_result.message)
Anderson-Darling统计量: 0.8746794117758157
临界值: [0.555 0.632 0.759 0.885 1.053]
数据不服从正态分布
--------------------------
----检验的结果包括Anderson-Darling统计量、临界值、显著性水平以及适配结果,用于判断数据是否服从正态分布-----
AndersonResult(statistic=0.8746794117758157, critical_values=array([0.555, 0.632, 0.759, 0.885, 1.053]), significance_level=array([15. , 10. , 5. , 2.5, 1. ]), fit_result= params: FitParams(loc=-0.00916569417046395, scale=1.012016300795819)
success: True
message: '`anderson` successfully fit the distribution to the data.')
<class 'scipy.stats._morestats.AndersonResult'>
--------------------------
Anderson-Darling统计量: 0.8746794117758157
临界值: [0.555 0.632 0.759 0.885 1.053]
显著性水平: [15. 10. 5. 2.5 1. ]
适配结果 params: FitParams(loc=-0.00916569417046395, scale=1.012016300795819)
适配结果 success: True
适配结果 message: `anderson` successfully fit the distribution to the data.
[Finished in 5.0s]
相关文章:

Anderson-Darling正态性检验【重要统计工具】
Anderson-Darling正态性检验是一种用于确定数据集是否服从正态分布(也称为高斯分布或钟形曲线分布)的统计方法。它基于Anderson和Darling于1954年提出的检验统计量。该检验的基本原理和用途如下: 基本原理: 零假设(Nu…...
Ubuntu基于Docker快速配置GDAL的Python、C++环境
本文介绍在Linux的Ubuntu操作系统中,基于Docker快速配置Python、C等不同编程语言均可用的地理数据处理库GDAL的方法。 首先,我们访问GDAL库的Docker镜像官方网站(https://github.com/OSGeo/gdal/tree/master/docker)。其中&#x…...

<C++> 哈希表模拟实现STL_unordered_set/map
哈希表模板参数的控制 首先需要明确的是,unordered_set是K模型的容器,而unordered_map是KV模型的容器。 要想只用一份哈希表代码同时封装出K模型和KV模型的容器,我们必定要对哈希表的模板参数进行控制。 为了与原哈希表的模板参数进行区分…...

【数据结构与算法】通过双向链表和HashMap实现LRU缓存 详解
这个双向链表采用的是有伪头节点和伪尾节点的 与上一篇文章中单链表的实现不同,区别于在实例化这个链表时就初始化了的伪头节点和伪尾节点,并相互指向,在第一次添加节点时,不需要再考虑空指针指向问题了。 /*** 通过链表与HashMa…...
MySQL的内置函数
文章目录 1. 聚合函数2. group by子句的使用3. 日期函数4. 字符串函5. 数学函数6. 其它函数 1. 聚合函数 COUNT([DISTINCT] expr) 返回查询到的数据的数量 用SELECT COUNT(*) FROM students或者SELECT COUNT(1) FROM students也能查询总个数。 统计本次考试的数学成绩分数去…...

数据结构与算法-(7)---栈的应用-(3)表达式转换
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
)
Lilliefors正态性检验(一种非参数统计方法)
Lilliefors检验(也称为Kolmogorov-Smirnov-Lilliefors检验)是一种用于检验数据是否符合正态分布的统计检验方法,它是Kolmogorov-Smirnov检验的一种变体,专门用于小样本情况。与K-S检验不同,Lilliefors检验不需要假定数…...
)
【云原生】配置Kubernetes CronJob自动备份MySQL数据库(单机版)
文章目录 每天自动备份数据库MySQL【云原生】配置Kubernetes CronJob自动备份Clickhouse数据库 每天自动备份数据库 MySQL 引用镜像:databack/mysql-backup,使用文档:https://hub.docker.com/r/databack/mysql-backup 测试、开发环境:每天0点40分执行全库备份操作,备份文…...
基于PSO算法的功率角摆动曲线优化研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
数论知识点总结(一)
文章目录 目录 文章目录 前言 一、数论有哪些 二、题法混讲 1.素数判断,质数,筛法 2.最大公约数和最小公倍数 3.快速幂 4.约数 前言 现在针对CSP-J/S组的第一题主要都是数论,换句话说,持数论之剑,可行天下矣! 一、数论有哪些 数论 原根,素数判断,质数,筛法最大公约数…...

知识分享 钡铼网关功能介绍:使用SSLTLS 加密,保证MQTT通信安全
背景 为了使不同的设备或系统能够相互通信,让旧有系统和新的系统可以集成,通信更加灵活和可靠。以及将数据从不同的来源收集并传输到不同的目的地,实现数据的集中管理和分发。 通信网关完美克服了这一难题,485或者网口的设备能通过…...

asp.net core mvc区域路由
ASP.NET Core 区域路由(Area Routing)是一种将应用程序中的路由划分为多个区域的方式,类似于 MVC 的控制器和视图的区域划分。区域路由可以帮助开发人员更好地组织应用程序的代码和路由,并使其更易于维护。 要使用区域路由&#…...
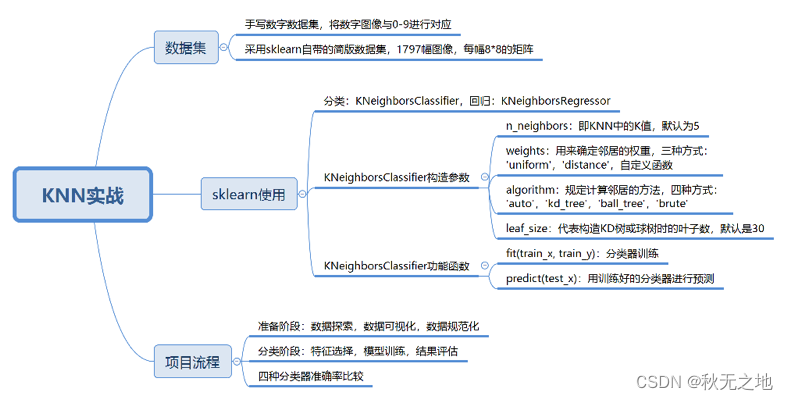
KNN(下):数据分析 | 数据挖掘 | 十大算法之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Servlet开发-session和cookie理解案例-登录页面
项目展示 进入登录页面,输入正确的用户名和密码以后会自动跳到主页 登录成功以后打印用户名以及上次登录的时间,如果浏览器和客户端都保存有上次登录的信息,则不需要登录就可以进入主页 编码思路 1.首先提供一个登录的前端页面&…...
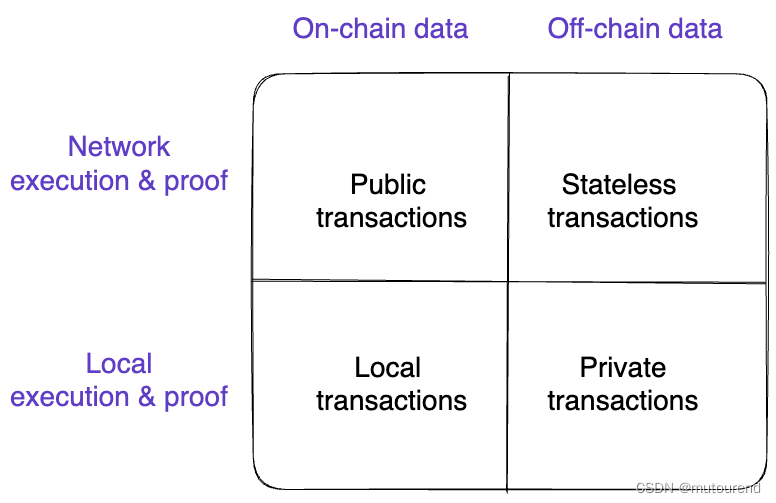
Polygon Miden:扩展以太坊功能集的ZK-optimized rollup
1. 引言 Polygon Miden定位为zkVM,定于2023年Q4上公开测试网。 zk、zkVM、zkEVM及其未来中指出,当前主要有3种类型的zkVM,括号内为其相应的指令集: mainstream(WASM, RISC-V)EVM(EVM bytecod…...

[题]宝物筛选 #单调队列优化
五、宝物筛选(洛谷P1776) 题目链接 好家伙,找到了一个之前学习多重背包优化时的错误…… 之前记的笔记还是很有用的…… #include<bits/stdc.h> using namespace std; const int N 1e5 10; int f[N]; int n, m; int v, w, s; int l…...

.NET的键盘Hook管理类,用于禁用键盘输入和切换
一、MyHook帮助类 此类需要编写指定屏蔽的按键,灵活性差。 using System; using System.Runtime.InteropServices; using System.Diagnostics; using System.Windows.Forms; using Microsoft.Win32;namespace MyHookClass {/// <summary>/// 类一/// </su…...

Anaconda Jupyter
🙌秋名山码民的主页 😂oi退役选手,Java、大数据、单片机、IoT均有所涉猎,热爱技术,技术无罪 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 获取源码,添加WX 目录 前言An…...
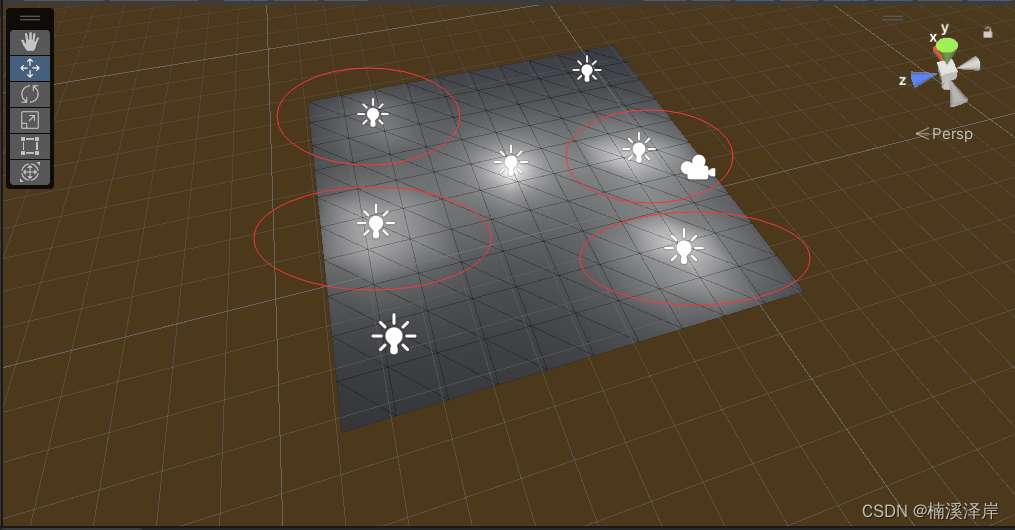
Unity中Shader的前向渲染路径ForwardRenderingPath
文章目录 前言一、前向渲染路径的特点二、渲染方式1、逐像素(效果最好)2、逐顶点(效果次之)3、SH球谐(效果最差) 三、Unity中对灯光设置 后,自动选择对应的渲染方式1、ForwardBase仅用于一个逐像素的平行灯,以及所有的逐顶点与SH2、ForwardAdd用于其他所…...

简历项目优化关键方法论-START
START方法论是非常著名的面试法则,经常被面试官使用的工具 Situation:情况、事情、项目需求是在什么情况下发生Task:任务,你负责的做的是什么Action:动作,针对这样的情况分析,你采用了什么行动方式Result:结果,在这样…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
