C++模板大全(持续更新,依不同网站整理而成)
C++模板大全
- 基本模板
- 快读
- 快写
- 快读快写
- 火车头
- 缺省源
- 基本算法
- 暴力枚举
- 模拟
- 贪心
- 二分
- 三分
- 尺取法
- 分治
- 前缀和
- 差分
- 递推
- 递归
- 倍增
- 排序
- sort
- 冒泡排序
- 桶排序
- 选择排序
- 插入排序
- 希尔排序
- 归并排序
- 快速排序
- 堆排序
- 计数排序
- 基数排序
- 基础数据结构
- 栈
- 队列
- 哈希
- 链表
- 单向链表
- 双向链表
- 单调栈
- 单调队列
- 高级数据结构
- 树
- 树的储存
- 求二叉树深度
- 求二叉树先序遍历
- 求二叉树中序遍历
- 求二叉树后序遍历
- 求二叉树层序遍历
- 哈弗曼树的创建
- 哈夫曼编码
- 树状数组
- 单修区查
- 区修单查
- 区修区查
- 线段树
- 单修区查
- 区修单查
- 区间加法
- 区间乘法
- 区间根号
- 并查集
- 普通并查集
- 路径压缩
- 按秩合并
- 树上问题
- 树的直径
- 树的重心
- LCA(最近公共祖先)
基本模板
快读
namespace IN{const int MAX_INPUT=1000000;#define getc()(p1==p2&&(p2=(p1=buf)+inbuf->sgetn(buf,MAX_INPUT),p1==p2)?EOF:*p1++)char buf[MAX_INPUT],*p1,*p2;template<typename T>inline bool read(T&x){static std::streambuf*inbuf=cin.rdbuf();x=0;register int f=0,flag=false;register char ch=getc();while(!isdigit(ch)){if(ch=='-'){f=1;}ch=getc();}if(isdigit(ch)){x=x*10+ch-'0';ch=getc();flag=true;}while(isdigit(ch)){x=x*10+ch-48;ch=getc();}x=f?-x:x;return flag;}template<typename T,typename ...Args>inline bool read(T&a,Args& ...args){return read(a)&&read(args...);}#undef getc
}
using namespace IN;
快写
namespace OUT{template<typename T>inline void put(T x){static std::streambuf *outbuf=cout.rdbuf();static char stack[21];static int top=0;if(x<0){outbuf->sputc('-');x=-x;}if(!x){outbuf->sputc('0');outbuf->sputc('\n');return;}while(x){stack[++top]=x%10+'0';x/=10;}while(top){outbuf->sputc(stack[top]);--top;}outbuf->sputc('\n');}inline void putc(const char ch){static std::streambuf *outbuf=cout.rdbuf();outbuf->sputc(ch);}inline void putstr(string s){for(register int i=0;i<s.length();i++) putc(s[i]);}template<typename T>inline void put(const char ch,T x){static std::streambuf *outbuf=cout.rdbuf();static char stack[21];static int top = 0;if(x<0){outbuf->sputc('-');x=-x;}if(!x){outbuf->sputc('0');outbuf->sputc(ch);return;}while(x){stack[++top]=x%10+'0';x/=10;}while(top){outbuf->sputc(stack[top]);--top;}outbuf->sputc(ch);}template<typename T,typename ...Args> inline void put(T a,Args ...args){put(a);put(args...);}template<typename T,typename ...Args> inline void put(const char ch,T a,Args ...args){put(ch,a);put(ch,args...);}
}
using namespace OUT;
快读快写
namespace IN{const int MAX_INPUT=1000000;#define getc()(p1==p2&&(p2=(p1=buf)+inbuf->sgetn(buf,MAX_INPUT),p1==p2)?EOF:*p1++)char buf[MAX_INPUT],*p1,*p2;template<typename T>inline bool read(T&x){static std::streambuf*inbuf=cin.rdbuf();x=0;register int f=0,flag=false;register char ch=getc();while(!isdigit(ch)){if(ch=='-'){f=1;}ch=getc();}if(isdigit(ch)){x=x*10+ch-'0';ch=getc();flag=true;}while(isdigit(ch)){x=x*10+ch-48;ch=getc();}x=f?-x:x;return flag;}template<typename T,typename ...Args>inline bool read(T&a,Args& ...args){return read(a)&&read(args...);}#undef getc
}
namespace OUT{template<typename T>inline void put(T x){static std::streambuf *outbuf=cout.rdbuf();static char stack[21];static int top=0;if(x<0){outbuf->sputc('-');x=-x;}if(!x){outbuf->sputc('0');outbuf->sputc('\n');return;}while(x){stack[++top]=x%10+'0';x/=10;}while(top){outbuf->sputc(stack[top]);--top;}outbuf->sputc('\n');}inline void putc(const char ch){static std::streambuf *outbuf=cout.rdbuf();outbuf->sputc(ch);}inline void putstr(string s){for(register int i=0;i<s.length();i++) putc(s[i]);}template<typename T>inline void put(const char ch,T x){static std::streambuf *outbuf=cout.rdbuf();static char stack[21];static int top = 0;if(x<0){outbuf->sputc('-');x=-x;}if(!x){outbuf->sputc('0');outbuf->sputc(ch);return;}while(x){stack[++top]=x%10+'0';x/=10;}while(top){outbuf->sputc(stack[top]);--top;}outbuf->sputc(ch);}template<typename T,typename ...Args> inline void put(T a,Args ...args){put(a);put(args...);}template<typename T,typename ...Args> inline void put(const char ch,T a,Args ...args){put(ch,a);put(ch,args...);}
}
using namespace IN;
using namespace OUT;
火车头
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC target("avx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
缺省源
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC target("avx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
#define int long long
#define ofr(x,y,z) for(int x=y;x<=z;x++)
#define rfr(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
namespace IN{const int MAX_INPUT=1000000;#define getc()(p1==p2&&(p2=(p1=buf)+inbuf->sgetn(buf,MAX_INPUT),p1==p2)?EOF:*p1++)char buf[MAX_INPUT],*p1,*p2;template<typename T>inline bool read(T&x){static std::streambuf*inbuf=cin.rdbuf();x=0;register int f=0,flag=false;register char ch=getc();while(!isdigit(ch)){if(ch=='-'){f=1;}ch=getc();}if(isdigit(ch)){x=x*10+ch-'0';ch=getc();flag=true;}while(isdigit(ch)){x=x*10+ch-48;ch=getc();}x=f?-x:x;return flag;}template<typename T,typename ...Args>inline bool read(T&a,Args& ...args){return read(a)&&read(args...);}#undef getc
}
namespace OUT{template<typename T>inline void put(T x){static std::streambuf *outbuf=cout.rdbuf();static char stack[21];static int top=0;if(x<0){outbuf->sputc('-');x=-x;}if(!x){outbuf->sputc('0');outbuf->sputc('\n');return;}while(x){stack[++top]=x%10+'0';x/=10;}while(top){outbuf->sputc(stack[top]);--top;}outbuf->sputc('\n');}inline void putc(const char ch){static std::streambuf *outbuf=cout.rdbuf();outbuf->sputc(ch);}inline void putstr(string s){for(register int i=0;i<s.length();i++){putc(s[i]);}}template<typename T>inline void put(const char ch,T x){static std::streambuf *outbuf=cout.rdbuf();static char stack[21];static int top=0;if(x<0){outbuf->sputc('-');x=-x;}if(!x){outbuf->sputc('0');outbuf->sputc(ch);return;}while(x){stack[++top]=x%10+'0';x/=10;}while(top){outbuf->sputc(stack[top]);--top;}outbuf->sputc(ch);}template<typename T,typename ...Args> inline void put(T a,Args ...args){put(a);put(args...);}template<typename T,typename ...Args> inline void put(const char ch,T a,Args ...args){put(ch,a);put(ch,args...);}
}
using namespace IN;
using namespace OUT;
void openfile(){freopen(".in","r",stdin);freopen(".out","w",stdout);
}
int main(){std::ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr);return 0;
}
emmm…下面开始回归正题了
基本算法
暴力枚举
抱歉,暴力枚举没有模板
模拟
抱歉,模拟没有模板.
贪心
抱歉,贪心没有模板
二分
注意,使用二分前要注意该序列的单调性.
while (l <= r) {mid = (l + r) >> 1;if (check(mid)) { //check为二分答案ans = mid;r = mid - 1;} else {l = mid + 1;}
}
另外,我们也可以使用lower_bound和upper_bound.
int j=lower_bound(a+1,a+n+1,m)-a;
int k=upper_bound(a+1,a+n+1,m)-a;
三分
三分主要用来求单峰函数或单谷函数的极值点
double l = 0, r = 1000;
while (r - l > esp) {double k = (r - l) / 3;double mid1 = l + k, mid2 = r - k;if (check(mid1) <= check(mid2)) {r = mid2;} else {l = mid1;}
}
尺取法
尺取法,也称双指针
int l = 0, r = k;
while (n - l >= k) {int t = r - l - a[r] + a[l];if (t < k) {ans += (r - l - k + 1);r++;} else {l++;}
}
分治
抱歉,分治没有模板
前缀和
最简单的模板
cin >> a[1];
int b[i] = a[1];
for (int i = 2; i <= n; i++) {cin >> a[i];b[i] = b[i - 1] + a[i];
}
差分
就只需要把上面的反过来就行了,许多数据结构都要用的差分的概念,例:树状数组.
递推
抱歉,递推没有模板.
递归
抱歉,递归没有模板.
倍增
我们会在后面的快速幂和LCA中遇到.
排序
sort
这个都知道
sort(a+1,a+n+1,cmp)//cmp为自定义函数
冒泡排序
for (int i = 1; i <= n - 1; i++) {for (int j = 1; j <= n - i + 1; j++) {if (a[j - 1] < a[j]) {int temp;temp = a[j];a[j] = a[j - 1];a[j - 1] = temp;//交换,当然,也可以用swap}}
}
桶排序
for (int i = 1; i <= n; i++) {cin >> m;a[m]++;
}
for (int i = 1001; i >= 0; i--) {if (a[i] >= 1) {for (int j = 1; j <= a[i]; j++) {cout << i << " ";}}
}
选择排序
for (int i = 0; i < len - 1; i++) {int min = i;for (int j = i + 1; j < len; j++) {if (arr[j] < arr[min]) {min = j;}}swap(arr[min], arr[i]);
}
插入排序
int j, key;
for (int i = 1; i < len; i++) {key = arr[i];j = i - 1;while ((j >= 0) && (arr[j] > key)) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;
}
希尔排序
int inc = len;do {// 确定分组的增量inc = inc / 3 + 1;for (int i = 0; i < inc; i++) {for (int j = i + inc; j < len; j += inc) {if (arr[j] < arr[j - inc]) {int temp = arr[j];for (int k = j - inc; k >= 0 && temp < arr[k]; k -= inc) {arr[k + inc] = arr[k];}arr[k + inc] = temp;}}}
} while (inc > 1);
归并排序
if (start >= end) {return;
}
int mid = (start + end) / 2;
MergeSort(arr, start, mid, temp);
MergeSort(arr, mid + 1, end, temp);
// 合并两个有序序列
int length = 0; // 表示辅助空间有多少个元素
int i_start = start;
int i_end = mid;
int j_start = mid + 1;
int j_end = end;
while (i_start <= i_end && j_start <= j_end) {if (arr[i_start] < arr[j_start]) {temp[length] = arr[i_start];length++;i_start++;} else {temp[length] = arr[j_start];length++;j_start++;}
}
while (i_start <= i_end) { // 把剩下数的合并temp[length] = arr[i_start];i_start++;length++;
}
while (j_start <= j_end) {temp[length] = arr[j_start];length++;j_start++;
}
// 把辅助空间的数据放到原空间
for (int i = 0; i < length; i++) {arr[start + i] = temp[i];
}
快速排序
if (start >= end) {return;
}
int i = start;
int j = end;
// 基准数
int baseval = arr[start];
while (i < j) {// 从右向左找比基准数小的数while (i < j && arr[j] >= baseval) {j--;}if (i < j) {arr[i] = arr[j];i++;}// 从左向右找比基准数大的数while (i < j && arr[i] < baseval) {i++;}if (i < j) {arr[j] = arr[i];j--;}
}
// 把基准数放到i的位置
arr[i] = baseval;
// 递归
QuickSort(arr, start, i - 1);
QuickSort(arr, i + 1, end);
堆排序
// 最大堆化函数
void max_heapify(int arr[], int start, int end) {// 建立父节点指标和子节点指标int dad = start;int son = dad * 2 + 1;while (son <= end) { // 若子节点指标在范围內才做比较// 先比较两个子节点大小,选择最大的if (son + 1 <= end && arr[son] < arr[son + 1]) son++;// 如果父节点大于子节点代表调整完毕,直接跳出函数if (arr[dad] > arr[son]) return;else { // 否则交换父子內容再继续子节点和父节点比较swap(&arr[dad], &arr[son]);dad = son;son = dad * 2 + 1;}}
}
// 堆排序函数
void heap_sort(int arr[], int len) {int i;// 初始化,i从最后一个父节点开始调整for (i = len / 2 - 1; i >= 0; i--)max_heapify(arr, i, len - 1);// 先将第一个元素和已排好元素前一位做交换,再重新调整,直到排序完毕for (i = len - 1; i > 0; i--) {swap(&arr[0], &arr[i]);max_heapify(arr, 0, i - 1);}
}
计数排序
void counting_sort(int *ini_arr, int *sorted_arr, int n) {int *count_arr = (int *)malloc(sizeof(int) * 100);int i, j, k;for (int k = 0; k < 100; k++){count_arr[k] = 0;}for (int i = 0; i < n; i++){count_arr[ini_arr[i]]++;}for (int k = 1; k < 100; k++){count_arr[k] += count_arr[k - 1];}for (j = n; j > 0; j--){sorted_arr[--count_arr[ini_arr[j - 1]]] = ini_arr[j - 1];}free(count_arr);
}
基数排序
void count_sort(int arr[], int n, int exp) {for (int i = 0; i < n; i++){count[(arr[i] / exp) % 10]++;}for (int i = 1; i < 10; i++){count[i] += count[i - 1];}for (int i = n - 1; i >= 0; i--) {output[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}for (int i = 0; i < n; i++){arr[i] = output[i];}
}
void radix_sort(int arr[], int n) {int max_val = arr[0];for (int i = 1; i < n; i++){if (arr[i] > max_val){max_val = arr[i];}}for (int exp = 1; max_val / exp > 0; exp *= 10){count_sort(arr, n, exp);}
}
基础数据结构
栈
STL容器:stack
具体操作用法上度娘
队列
STL容器:queue
具体操作方法上度娘
哈希
你想怎么哈希就怎么哈希,只要不保证冲突过多就行.
链表
单向链表
// 节点类
template <typename T>
class Node {
public:T data;Node<T>* next;Node(T data) {this->data = data;next = nullptr;}
};
// 链表类
template <typename T>
class LinkedList {
private:Node<T>* head;Node<T>* tail;int size;
public:LinkedList() {head = nullptr;tail = nullptr;size = 0;}void add(T data) {Node<T>* new_node = new Node<T>(data);if (size == 0) {head = new_node;tail = new_node;} else {tail->next = new_node;tail = new_node;}size++;}void remove(T data) {Node<T>* prev = nullptr;Node<T>* curr = head;while (curr != nullptr && curr->data != data) {prev = curr;curr = curr->next;}if (curr != nullptr) {if (prev == nullptr) {head = curr->next;} else {prev->next = curr->next;}delete curr;size--;}}void print() {Node<T>* curr = head;while (curr != nullptr) {cout << curr->data << " ";curr = curr->next;}cout << endl;}
};
双向链表
// 节点类
template <typename T>
class Node {
public:T data;Node<T>* prev;Node<T>* next;Node(T data) {this->data = data;prev = nullptr;next = nullptr;}
};
// 链表类
template <typename T>
class DoublyLinkedList {
private:Node<T>* head;Node<T>* tail;int size;
public:DoublyLinkedList() {head = nullptr;tail = nullptr;size = 0;}void add(T data) {Node<T>* new_node = new Node<T>(data);if (size == 0) {head = new_node;tail = new_node;new_node->prev = nullptr;new_node->next = nullptr;} else {new_node->prev = tail;new_node->next = nullptr;tail->next = new_node;tail = new_node;}size++;}void remove(T data) {Node<T>* prev = nullptr;Node<T>* curr = head;while (curr != nullptr && curr->data != data) {prev = curr;curr = curr->next;}if (curr != nullptr) {if (prev == nullptr) {head = curr->next;if (head != nullptr) {head->prev = nullptr;}} else {prev->next = curr->next;if (curr->next != nullptr) {curr->next->prev = prev;}}delete curr;size--;}}void print() {Node<T>* curr = head;while (curr != nullptr) {cout << curr->data << " ";curr = curr->next;}cout << endl;}
};
单调栈
同时也可以用数组来模拟单调栈
for(int i = 1; i <= a.size(); i++) {while(!s.empty() && a[i-1] > s.top()) {s.pop();}s.push(a[i-1]);
}
单调队列
同时也可以用数组来模拟单调队列
for (int i = k; i < n; ++i) {q.emplace(nums[i], i);while (q.top().second <= i - k) {q.pop();}ans.push_back(q.top().first);
}
高级数据结构
树
树的储存
for (int i=1;i<=n;i++) {cin>>child>>father;a[child].parent=father;a[father].children.push_back(child);
}
求二叉树深度
void dfs(int x,int deep) {d=max(d,deep);if(a[x].left) {dfs(a[x].left,deep+1);}if(a[x].right) {dfs(a[x].right,deep+1);}
}
求二叉树先序遍历
void recursion(struct BinaryNode *root) {if(root==NULL) {return;}printf("%c\n",root->ch);recursion(root->lChild);recursion(root->rChild);
}
求二叉树中序遍历
void recursion(struct BinaryNode *root) {if(root==NULL) {return;}recursion(root->lChild);printf("%c\n",root->ch);recursion(root->rChild);
}
求二叉树后序遍历
void recursion(struct BinaryNode *root) {if(root==NULL) {return;}recursion(root->lChild);recursion(root->rChild);printf("%c\n",root->ch);
}
求二叉树层序遍历
if (Tree != NULL) {q.push(Tree);//根节点进队列
}
while (q.empty() == false) //队列不为空判断 {cout << q.front()->data << " → ";if (q.front()->leftPtr != NULL) //如果有左孩子,leftChild入队列 {q.push(q.front()->leftPtr);}if (q.front()->rightPtr != NULL) //如果有右孩子,rightChild入队列 {q.push(q.front()->rightPtr);}q.pop();//已经遍历过的节点出队列
}
哈弗曼树的创建
其中 q q q 是优先队列.
int huffman(int x) {int res=0;for (int i=0;i<n-1;i++) {int x=q.top();q.pop();int y=q.top();q.pop();int add=x+y;res+=add;q.push(add);}return res;
}
哈夫曼编码
void huffmanCoding(Htree root, int len, int arr[]) {// 计算霍夫曼编码if (root != NULL) {if (root->lchild == NULL && root->rchild == NULL) {for (int i = 0; i < len; i++) printf("%d", arr[i]);printf("\n");} else {arr[len] = 0;huffmanCoding(root->lchild, len + 1, arr);arr[len] = 1;huffmanCoding(root->rchild, len + 1, arr);}}
}
树状数组
单修区查
#include<bits/stdc++.h>
using namespace std;
int const maxn=500005;
int n,m,p,x,y;
long long a,c[maxn];
long long lowbit(int x) {return x&-x;
}
void add(int u,int v) {for (int i=u;i<=n;i+=lowbit(i)) {c[i]+=v;}
}
long long sum(int u) {int ans=0;for (int i=u;i>0;i-=lowbit(i)) {ans+=c[i];}return ans;
}
int main() {cin>>n>>m;for (int i=1;i<=n;i++) {cin>>a;add(i,a);}for (int i=1;i<=m;i++) {cin>>p>>x>>y;if(p==1) {add(x,y);}if(p==2) {cout<<sum(y)-sum(x-1)<<endl;}}return 0;
}
区修单查
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
using ll=long long;
long long n,q,f,a[1000005],l,r,x,p,b[1000005];
long long c[1000005];
int main() {cin>>n>>q;for (int i=1;i<=n;i++) {cin>>a[i];b[i]=a[i]-a[i-1];for (int j=i;j<=n;j+=lowbit(j)) {c[j]+=b[i];}}for (int i=1;i<=q;i++) {cin>>f;if(f==1) {cin>>l>>r>>x;for (int j=l;j<=n;j+=lowbit(j)) {c[j]+=x;}for (int j=r+1;j<=n;j+=lowbit(j)) {c[j]-=x;}} else {cin>>p;long long ans=0;for (int j=p;j>=1;j-=lowbit(j)) {ans+=c[j];}cout<<ans<<endl;}}return 0;
}
区修区查
#include<bits/stdc++.h>
#define lowbit(x) x&(-x)
using namespace std;
long long n,m,f,l,r,x,a[1000005],b;
long long c1[1000005],c2[1000005];
void update(long long x,long long k) {for (long long i=x;i<=n;i+=lowbit(i)) {c1[i]+=k,c2[i]+=k*(x-1);}
}
long long getsum(long long x) {long long ans=0;for (long long i=x;i>=1;i-=lowbit(i)) {ans+=(c1[i]*x-c2[i]);}return ans;
}
int main() {cin>>n>>m;for (long long i=1;i<=n;i++) {cin>>a[i];b=a[i]-a[i-1];update(i,b);}for (long long i=1;i<=m;i++) {cin>>f>>l>>r;if(f==1) {cin>>x;update(l,x);update(r+1,-x);} else {cout<<getsum(r)-getsum(l-1)<<endl;}}return 0;
}
线段树
单修区查
#include <bits/stdc++.h>
using namespace std;
#define MAXN 100010
#define INF 10000009
#define MOD 10000007
#define LL long long
#define in(a) a=read()
#define REP(i,k,n) for (long long i=k;i<=n;i++)
#define DREP(i,k,n) for (long long i=k;i>=n;i--)
#define cl(a) memset(a,0,sizeof(a))
inline long long read() {long long x=0,f=1;char ch=getchar();for (;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;for (;isdigit(ch);ch=getchar()) x=x*10+ch-'0';return x*f;
}
inline void out(long long x) {if(x<0) putchar('-'),x=-x;if(x>9) out(x/10);putchar(x%10+'0');
}
long long n,m,p;
long long input[MAXN];
struct node {long long l,r;long long sum,mlz,plz;
}
tree[4*MAXN];
inline void build(long long i,long long l,long long r) {tree[i].l=l;tree[i].r=r;tree[i].mlz=1;if(l==r) {tree[i].sum=input[l]%p;return ;}long long mid=(l+r)>>1;build(i<<1,l,mid);build(i<<1|1,mid+1,r);tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;return ;
}
inline void pushdown(long long i) {long long k1=tree[i].mlz,k2=tree[i].plz;tree[i<<1].sum=(tree[i<<1].sum*k1+k2*(tree[i<<1].r-tree[i<<1].l+1))%p;tree[i<<1|1].sum=(tree[i<<1|1].sum*k1+k2*(tree[i<<1|1].r-tree[i<<1|1].l+1))%p;tree[i<<1].mlz=(tree[i<<1].mlz*k1)%p;tree[i<<1|1].mlz=(tree[i<<1|1].mlz*k1)%p;tree[i<<1].plz=(tree[i<<1].plz*k1+k2)%p;tree[i<<1|1].plz=(tree[i<<1|1].plz*k1+k2)%p;tree[i].plz=0;tree[i].mlz=1;return ;
}
inline void mul(long long i,long long l,long long r,long long k) {if(tree[i].r<l || tree[i].l>r) return ;if(tree[i].l>=l && tree[i].r<=r) {tree[i].sum=(tree[i].sum*k)%p;tree[i].mlz=(tree[i].mlz*k)%p;tree[i].plz=(tree[i].plz*k)%p;return ;}pushdown(i);if(tree[i<<1].r>=l) mul(i<<1,l,r,k);if(tree[i<<1|1].l<=r) mul(i<<1|1,l,r,k);tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;return ;
}
inline void add(long long i,long long l,long long r,long long k) {if(tree[i].r<l || tree[i].l>r) return ;if(tree[i].l>=l && tree[i].r<=r) {tree[i].sum+=((tree[i].r-tree[i].l+1)*k)%p;tree[i].plz=(tree[i].plz+k)%p;return ;}pushdown(i);if(tree[i<<1].r>=l) add(i<<1,l,r,k);if(tree[i<<1|1].l<=r) add(i<<1|1,l,r,k);tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;return ;
}
inline long long search(long long i,long long l,long long r) {if(tree[i].r<l || tree[i].l>r) return 0;if(tree[i].l>=l && tree[i].r<=r)return tree[i].sum;pushdown(i);long long sum=0;if(tree[i<<1].r>=l) sum+=search(i<<1,l,r)%p;if(tree[i<<1|1].l<=r) sum+=search(i<<1|1,l,r)%p;return sum%p;
}
int main() {in(n);in(m);in(p);REP(i,1,n) in(input[i]);build(1,1,n);REP(i,1,m) {long long fl,a,b,c;in(fl);if(fl==1) {in(a);in(b);in(c);c%=p;mul(1,a,b,c);}if(fl==2) {in(a);in(b);in(c);c%=p;add(1,a,b,c);}if(fl==3) {in(a);in(b);printf("%lld\n",search(1,a,b));}}return 0;
}
区修单查
#include <bits/stdc++.h>
using namespace std;
int n,m;
int ans;
int input[500010];
struct node {int left,right;int num;
}
tree[2000010];
void build(int left,int right,int index) {tree[index].num=0;tree[index].left=left;tree[index].right=right;if(left==right)return ;int mid=(right+left)/2;build(left,mid,index*2);build(mid+1,right,index*2+1);
}
void pls(int index,int l,int r,int k) {if(tree[index].left>=l && tree[index].right<=r) {tree[index].num+=k;return ;}if(tree[index*2].right>=l)pls(index*2,l,r,k);if(tree[index*2+1].left<=r)pls(index*2+1,l,r,k);
}
void search(int index,int dis) {ans+=tree[index].num;if(tree[index].left==tree[index].right)return ;if(dis<=tree[index*2].right)search(index*2,dis);if(dis>=tree[index*2+1].left)search(index*2+1,dis);
}
int main() {int n,m;cin>>n>>m;build(1,n,1);for (int i=1;i<=n;i++)scanf("%d",&input[i]);for (int i=1;i<=m;i++) {int a;scanf("%d",&a);if(a==1) {int x,y,z;scanf("%d%d%d",&x,&y,&z);pls(1,x,y,z);}if(a==2) {ans=0;int x;scanf("%d",&x);search(1,x);printf("%d\n",ans+input[x]);}}
}
区间加法
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e6+7;
const ll mod=2147483647;
ll n,m;
struct node {ll l,r,sum,lz;
}
tree[N];
ll arr[N];
void build(ll i,ll l,ll r,ll arr[]) {tree[i].lz=0;//初始化的时候肯定都是0tree[i].l=l;tree[i].r=r;if(l==r) {tree[i].sum=arr[l];//到达底部单节点才把输入的值赋给你return ;}ll mid=(l+r)/2;build(i*2,l,mid,arr);build(i*2+1,mid+1,r,arr);tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//树已经全部建完了,再从下往上+++,使得上层的树都有了值return ;
}
inline void push_down(ll i) {if(tree[i].lz!=0) {tree[i*2].lz+=tree[i].lz;tree[i*2+1].lz+=tree[i].lz;ll mid=(tree[i].l+tree[i].r)/2;tree[i*2].sum+=tree[i].lz*(mid-tree[i*2].l+1);tree[i*2+1].sum+=tree[i].lz*(tree[i*2+1].r-mid);tree[i].lz=0;}return ;
}
inline void add(ll i,ll l,ll r,ll k) {if(tree[i].l>=l&&tree[i].r<=r) {tree[i].sum+=k*(tree[i].r-tree[i].l+1);tree[i].lz+=k;return ;}push_down(i);if(tree[i*2].r>=l)add(i*2,l,r,k);if(tree[i*2+1].l<=r)add(i*2+1,l,r,k);tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;return ;
}
inline ll searchs(ll i,ll l, ll r) {if(tree[i].l>=l&&tree[i].r<=r)return tree[i].sum;push_down(i);ll num=0;if(tree[i*2].r>=l)num+=searchs(i*2,l,r);if(tree[i*2+1].l<=r)num+=searchs(i*2+1,l,r);return num;
}
int main() {ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m;for (int i=1;i<=n;++i)cin>>arr[i];build(1,1,n,arr);//从根节点开始建树for (int i=1;i<=m;++i) {ll tmp;cin>>tmp;if(tmp==1) {ll a,b,c;cin>>a>>b>>c;add(1,a,b,c);//每次修改都是从编号为1开始的,因为编号1是树的顶端,往下分叉}if(tmp==2) {ll a,b;cin>>a>>b;printf("%lld\n",searchs(1,a,b));//编号i的话,每次都是从1开始}}return 0;
}
区间乘法
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e6+7;
template<typename T>void read(T &x) {x=0;char ch=getchar();ll f=1;while(!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}x*=f;
}
ll n,m,arr[N],mod,flag,cn,cm,cw;
struct node {ll l,r,sum,mul,add;//有乘有加,先乘后加
}
tree[N];
inline void build(ll i,ll l,ll r) {tree[i].l=l;tree[i].r=r;tree[i].mul=1;if(l==r) {tree[i].sum=arr[l]%mod;return ;}ll mid=(l+r)>>1;build(i*2,l,mid);build(i*2+1,mid+1,r);tree[i].sum=(tree[i*2].sum+tree[i*2+1].sum)%mod;
}
inline void push_down(ll i) {tree[i*2].sum=(ll)(tree[i].mul*tree[i*2].sum+((tree[i*2].r-tree[i*2].l+1)*tree[i].add)%mod)%mod;tree[i*2+1].sum=(ll)(tree[i].mul*tree[i*2+1].sum+((tree[i*2+1].r-tree[i*2+1].l+1)*tree[i].add)%mod)%mod;tree[i*2].mul=(ll)(tree[i*2].mul*tree[i].mul)%mod;tree[i*2+1].mul=(ll)(tree[i*2+1].mul*tree[i].mul)%mod;tree[i*2].add=(ll)(tree[i*2].add*tree[i].mul+tree[i].add)%mod;tree[i*2+1].add=(ll)(tree[i*2+1].add*tree[i].mul+tree[i].add)%mod;tree[i].mul=1;tree[i].add=0;
}
inline void add(ll i,ll l,ll r,ll k) {if(tree[i].l>=l&&tree[i].r<=r) {tree[i].add=(ll)(tree[i].add+k)%mod;tree[i].sum=(ll)(tree[i].sum+k*(tree[i].r-tree[i].l+1))%mod;return ;}push_down(i);if(tree[i*2].r>=l)add(i*2,l,r,k);if(tree[i*2+1].l<=r)add(i*2+1,l,r,k);//ll mid=(tree[i].l+tree[i].r)>>1;//if(l<=mid)add(i*2,l,r,k);//if(mid<r)add(i*2+1,l,r,k);tree[i].sum=(tree[i*2].sum+tree[i*2+1].sum)%mod;
}
inline void mult(ll i,ll l,ll r,ll k) {if(tree[i].l>=l&&tree[i].r<=r) {tree[i].mul=(tree[i].mul*k)%mod;tree[i].add=(tree[i].add*k)%mod;tree[i].sum=(tree[i].sum*k)%mod;return ;}push_down(i);if(tree[i*2].r>=l)mult(i*2,l,r,k);if(tree[i*2+1].l<=r)mult(i*2+1,l,r,k);//ll mid=(tree[i].l+tree[i].r)>>1;//if(l<=mid)mult(i*2,l,r,k);//if(mid<r)mult(i*2+1,l,r,k);tree[i].sum=(tree[i*2].sum+tree[i*2+1].sum)%mod;
}
inline ll query(ll i,ll l,ll r) {if(tree[i].l>=l&&tree[i].r<=r)return tree[i].sum;push_down(i);ll num=0;if(tree[i*2].r>=l)num=(num+query(i*2,l,r))%mod;if(tree[i*2+1].l<=r)num=(num+query(i*2+1,l,r))%mod;return num;//ll val=0;//ll mid=(tree[i].l+tree[i].r)>>1;//if(l<=mid)val=(val+query(i*2,l,r))%mod;//if(mid<r)val=(val+query(i*2+1,l,r))%mod;//return val;
}
int main() {read(n),read(m),read(mod);for (int i=1;i<=n;++i)read(arr[i]);build(1,1,n);for (int i=1;i<=m;++i) {read(flag);if(flag==1) {read(cn),read(cm),read(cw);mult(1,cn,cm,cw);} else if(flag==2) {read(cn),read(cm),read(cw);add(1,cn,cm,cw);} else {read(cn),read(cm);cout<<query(1,cn,cm)<<endl;}}
}
区间根号
#include<bits/stdc++.h>
#define MAXN 1000010
#define REP(i,k,n) for (int i=k;i<=n;i++)
#define in(a) a=read()
using namespace std;
int read() {int x=0,f=1;char ch=getchar();for (;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;for (;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f;
}
struct node {int l,r;long long lz,sum,maxx,minn;
}
tree[MAXN<<2];
int n,m,input[MAXN];
inline void build(int i,int l,int r) {tree[i].l=l;tree[i].r=r;if(l==r) {tree[i].sum=tree[i].minn=tree[i].maxx=input[l];return ;}int mid=(l+r)>>1;build(i*2,l,mid);build(i*2+1,mid+1,r);tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;tree[i].minn=min(tree[i*2].minn,tree[i*2+1].minn);tree[i].maxx=max(tree[i*2].maxx,tree[i*2+1].maxx);return ;
}
inline void push_down(int i) {if(!tree[i].lz) return ;long long k=tree[i].lz;tree[i*2].lz+=k;tree[i*2+1].lz+=k;tree[i*2].sum-=(tree[i*2].r-tree[i*2].l+1)*k;tree[i*2+1].sum-=(tree[i*2+1].r-tree[i*2+1].l+1)*k;tree[i*2].minn-=k;tree[i*2+1].minn-=k;tree[i*2].maxx-=k;tree[i*2+1].maxx-=k;tree[i].lz=0;return ;
}
inline void Sqrt(int i,int l,int r) {if(tree[i].l>=l && tree[i].r<=r && (tree[i].minn-(long long)sqrt(tree[i].minn))==(tree[i].maxx-(long long)sqrt(tree[i].maxx))) {long long u=tree[i].minn-(long long)sqrt(tree[i].minn);tree[i].lz+=u;tree[i].sum-=(tree[i].r-tree[i].l+1)*u;tree[i].minn-=u;tree[i].maxx-=u;//cout<<"i"<<i<<" "<<tree[i].sum<<endl;return ;}if(tree[i].r<l || tree[i].l>r) return ;push_down(i);if(tree[i*2].r>=l) Sqrt(i*2,l,r);if(tree[i*2+1].l<=r) Sqrt(i*2+1,l,r);tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;tree[i].minn=min(tree[i*2].minn,tree[i*2+1].minn);tree[i].maxx=max(tree[i*2].maxx,tree[i*2+1].maxx);//cout<<"i"<<i<<" "<<tree[i].sum<<endl;return ;
}
inline long long search(int i,int l,int r) {if(tree[i].l>=l && tree[i].r<=r)return tree[i].sum;if(tree[i].r<l || tree[i].l>r) return 0;push_down(i);long long s=0;if(tree[i*2].r>=l) s+=search(i*2,l,r);if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);return s;
}
int main() {in(n);REP(i,1,n) in(input[i]);build(1,1,n);in(m);int a,b,c;REP(i,1,m) {in(a);in(b);in(c);if(a==1)printf("%lld\n",search(1,b,c));if(a==2) {Sqrt(1,b,c);//for(int i=1;i<=7;i++)// cout<<tree[i].sum<<" ";// cout<<endl;}}
}
并查集
普通并查集
int find(int x) {return fa[x]==x?x:find(fa[x]);
}
路径压缩
int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);
}
按秩合并
void rank(int x,int y) {int xx=find(x);int yy=find(y);if(xx!=yy) {if(rk[xx]<rk[yy]) {fa[xx]=yy;} else if(rk[ry]<rk[rx]) {fa[yy]=xx;} else {fa[xx]=yy;rk[yy]++;}}
}
树上问题
树的直径
有两种实现方法,一种是dfs,另一种是树形dp.
先放第一种dfs的.
const int N = 10000 + 10;
int n, c, d[N];
vector<int> E[N];
void dfs(int u, int fa) {for (int v : E[u]) {if (v == fa) continue;d[v] = d[u] + 1;if (d[v] > d[c]) c = v;dfs(v, u);}
}
int main() {scanf("%d", &n);for (int i = 1; i < n; i++) {int u, v;scanf("%d %d", &u, &v);E[u].push_back(v), E[v].push_back(u);}dfs(1, 0);d[c] = 0, dfs(c, 0);printf("%d\n", d[c]);return 0;
}
然后是树形dp
const int N = 10000 + 10;
int n, d = 0;
int d1[N], d2[N];
vector<int> E[N];
void dfs(int u, int fa) {d1[u] = d2[u] = 0;for (int v : E[u]) {if (v == fa) continue;dfs(v, u);int t = d1[v] + 1;if (t > d1[u])d2[u] = d1[u], d1[u] = t; else if (t > d2[u])d2[u] = t;}d = max(d, d1[u] + d2[u]);
}
int main() {scanf("%d", &n);for (int i = 1; i < n; i++) {int u, v;scanf("%d %d", &u, &v);E[u].push_back(v), E[v].push_back(u);}dfs(1, 0);printf("%d\n", d);return 0;
}
树的重心
// 这份代码默认节点编号从 1 开始,即 i ∈ [1,n]
int size[MAXN], // 这个节点的「大小」(所有子树上节点数 + 该节点)
weight[MAXN], // 这个节点的「重量」
centroid[2];
// 用于记录树的重心(存的是节点编号)
void GetCentroid(int cur, int fa) {// cur 表示当前节点 (current)size[cur] = 1;weight[cur] = 0;for (int i = head[cur]; i != -1; i = e[i].nxt) {if (e[i].to != fa) {// e[i].to 表示这条有向边所通向的节点。GetCentroid(e[i].to, cur);size[cur] += size[e[i].to];weight[cur] = max(weight[cur], size[e[i].to]);}}weight[cur] = max(weight[cur], n - size[cur]);if (weight[cur] <= n / 2) {// 依照树的重心的定义统计centroid[centroid[0] != 0] = cur;}
}
LCA(最近公共祖先)
求最近公共祖先有两种方法,一种是倍增,另一种是tarjan.
我们先放第一种倍增的做法.
#include <bits/stdc++.h>
#define MXN 50007
using namespace std;
std::vector<int> v[MXN];
std::vector<int> w[MXN];
int fa[MXN][31], cost[MXN][31], dep[MXN];
int n, m;
int a, b, c;
// dfs,用来为 lca 算法做准备。接受两个参数:dfs 起始节点和它的父亲节点。
void dfs(int root, int fno) {// 初始化:第 2^0 = 1 个祖先就是它的父亲节点,dep 也比父亲节点多 1。fa[root][0] = fno;dep[root] = dep[fa[root][0]] + 1;// 初始化:其他的祖先节点:第 2^i 的祖先节点是第 2^(i-1) 的祖先节点的第// 2^(i-1) 的祖先节点。for (int i = 1; i < 31; ++i) {fa[root][i] = fa[fa[root][i - 1]][i - 1];cost[root][i] = cost[fa[root][i - 1]][i - 1] + cost[root][i - 1];}// 遍历子节点来进行 dfs。int sz = v[root].size();for (int i = 0; i < sz; ++i) {if (v[root][i] == fno) continue;cost[v[root][i]][0] = w[root][i];dfs(v[root][i], root);}
}
// lca。用倍增算法算取 x 和 y 的 lca 节点。
int lca(int x, int y) {// 令 y 比 x 深。if (dep[x] > dep[y]) swap(x, y);// 令 y 和 x 在一个深度。int tmp = dep[y] - dep[x], ans = 0;for (int j = 0; tmp; ++j, tmp >>= 1)if (tmp & 1) ans += cost[y][j], y = fa[y][j];// 如果这个时候 y = x,那么 x,y 就都是它们自己的祖先。if (y == x) return ans;// 不然的话,找到第一个不是它们祖先的两个点。for (int j = 30; j >= 0 && y != x; --j) {if (fa[x][j] != fa[y][j]) {ans += cost[x][j] + cost[y][j];x = fa[x][j];y = fa[y][j];}}// 返回结果。ans += cost[x][0] + cost[y][0];return ans;
}
int main() {// 初始化表示祖先的数组 fa,代价 cost 和深度 dep。memset(fa, 0, sizeof(fa));memset(cost, 0, sizeof(cost));memset(dep, 0, sizeof(dep));// 读入树:节点数一共有 n 个。scanf("%d", &n);for (int i = 1; i < n; ++i) {scanf("%d %d %d", &a, &b, &c);++a, ++b;v[a].push_back(b);v[b].push_back(a);w[a].push_back(c);w[b].push_back(c);}// 为了计算 lca 而使用 dfs。dfs(1, 0);// 查询 m 次,每一次查找两个节点的 lca 点。scanf("%d", &m);for (int i = 0; i < m; ++i) {scanf("%d %d", &a, &b);++a, ++b;printf("%d\n", lca(a, b));}return 0;
}
第二种是tarjan做法
#include <bits/stdc++.h>
using namespace std;
class Edge {public:int toVertex, fromVertex;int next;int LCA;Edge() : toVertex(-1), fromVertex(-1), next(-1), LCA(-1) {};Edge(int u, int v, int n) : fromVertex(u), toVertex(v), next(n), LCA(-1) {};
};
const int MAX = 100;
int head[MAX], queryHead[MAX];
Edge edge[MAX], queryEdge[MAX];
int parent[MAX], visited[MAX];
int vertexCount, edgeCount, queryCount;
void init() {for (int i = 0; i <= vertexCount; i++) {parent[i] = i;}
}
int find(int x) {if (parent[x] == x) {return x;} else {return find(parent[x]);}
}
void tarjan(int u) {parent[u] = u;visited[u] = 1;for (int i = head[u]; i != -1; i = edge[i].next) {Edge& e = edge[i];if (!visited[e.toVertex]) {tarjan(e.toVertex);parent[e.toVertex] = u;}}for (int i = queryHead[u]; i != -1; i = queryEdge[i].next) {Edge& e = queryEdge[i];if (visited[e.toVertex]) {queryEdge[i ^ 1].LCA = e.LCA = find(e.toVertex);}}
}
int main() {memset(head, 0xff, sizeof(head));memset(queryHead, 0xff, sizeof(queryHead));cin >> vertexCount >> edgeCount >> queryCount;int count = 0;for (int i = 0; i < edgeCount; i++) {int start = 0, end = 0;cin >> start >> end;edge[count] = Edge(start, end, head[start]);head[start] = count;count++;edge[count] = Edge(end, start, head[end]);head[end] = count;count++;}count = 0;for (int i = 0; i < queryCount; i++) {int start = 0, end = 0;cin >> start >> end;queryEdge[count] = Edge(start, end, queryHead[start]);queryHead[start] = count;count++;queryEdge[count] = Edge(end, start, queryHead[end]);queryHead[end] = count;count++;}init();tarjan(1);for (int i = 0; i < queryCount; i++) {Edge& e = queryEdge[i * 2];cout << "(" << e.fromVertex << "," << e.toVertex << ") " << e.LCA << endl;}return 0;
}
目前先整理到这了,下次整理剩下的
相关文章:
)
C++模板大全(持续更新,依不同网站整理而成)
C模板大全 基本模板快读快写快读快写火车头缺省源 基本算法暴力枚举模拟贪心二分三分尺取法分治前缀和差分递推递归倍增排序sort冒泡排序桶排序选择排序插入排序希尔排序归并排序快速排序堆排序计数排序基数排序 基础数据结构栈队列哈希链表单向链表双向链表 单调栈单调队列 高…...
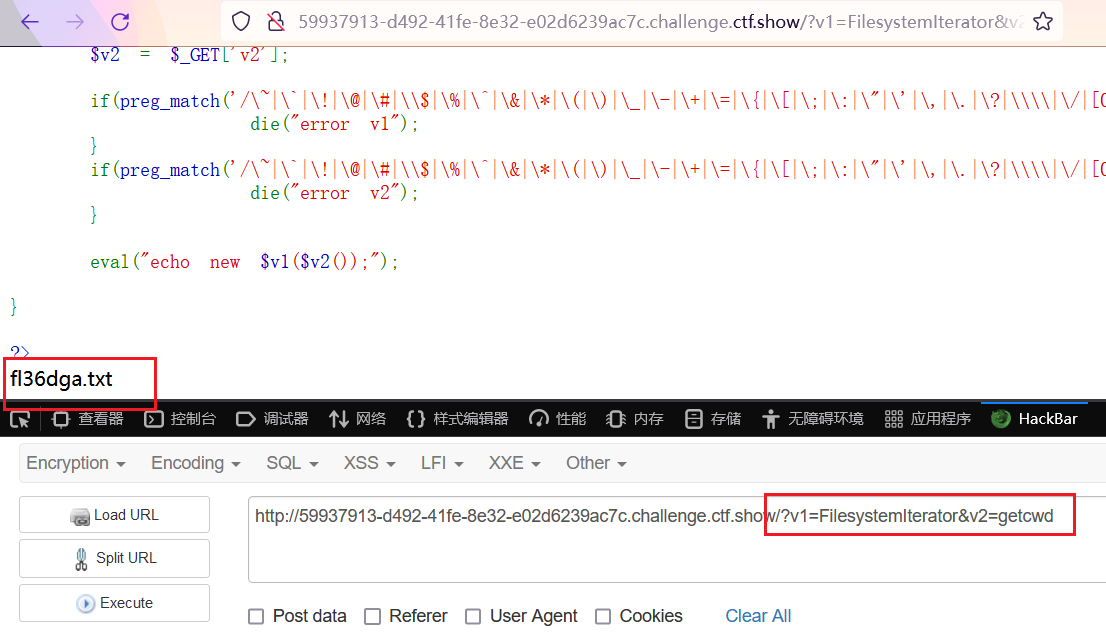
《CTFshow-Web入门》10. Web 91~110
Web 入门 索引web91题解总结 web92题解总结 web93题解 web94题解 web95题解 web96题解 web97题解 web98题解 web99题解总结 web100题解 web101题解 web102题解 web103题解 web104题解 web105题解总结 web106题解 web107题解 web108题解 web109题解 web110题解 ctf - web入门 索…...
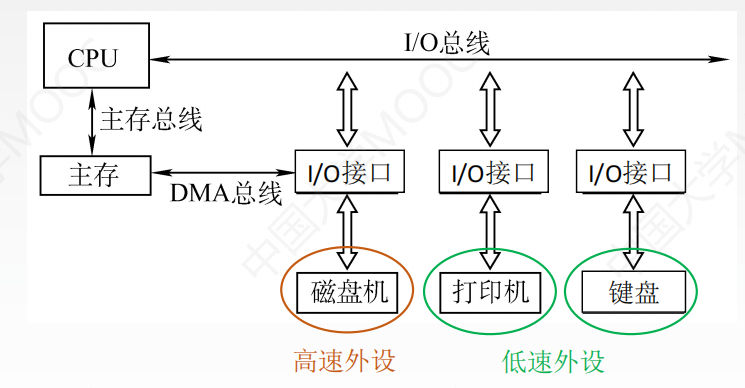
计组--总线
一、概念 总线是一组能为多个部件分时共享的公共信息传送线路。 共享是指总线上可以挂接多个部件,各个部件之间互相交换的信息都可以通过这组线路分时共享。 分时是指同一时刻只允许有一个部件向总线发送信息,如果系统中有多个部件,则它们…...

Git中的HEAD
Git中的HEAD HEAD^数字:表示当前提交的父提交,具体是第几个父提交通过数字指定,HEAD^1第一个父提交,该语法只 能用于合并(merge)的提交记录,因为一个通过合并产生的commit对象才有多个父提交。 HEAD~数字࿱…...
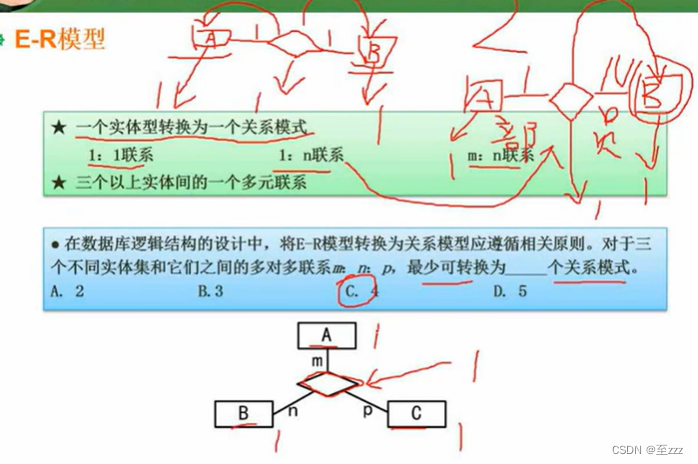
软件设计师_数据库系统_学习笔记
文章目录 3.1 数据库模式3.1.1 三级模式 两级映射3.1.2 数据库设计过程 3.2 ER模型3.3 关系代数与元组演算3.4 规范化理论3.5 并发控制3.6 数据库完整性约束3.7 分布式数据库3.8 数据仓库与数据挖掘 3.1 数据库模式 3.1.1 三级模式 两级映射 内模式直接与物理数据库相关联的 定…...

毛玻璃态计算器
效果展示 页面结构组成 从上述的效果可以看出,计算机的页面比较规整,适合grid布局。 CSS3 知识点 grid 布局 实现计算机布局 <div class"container"><form class"calculator" name"calc"><input type…...
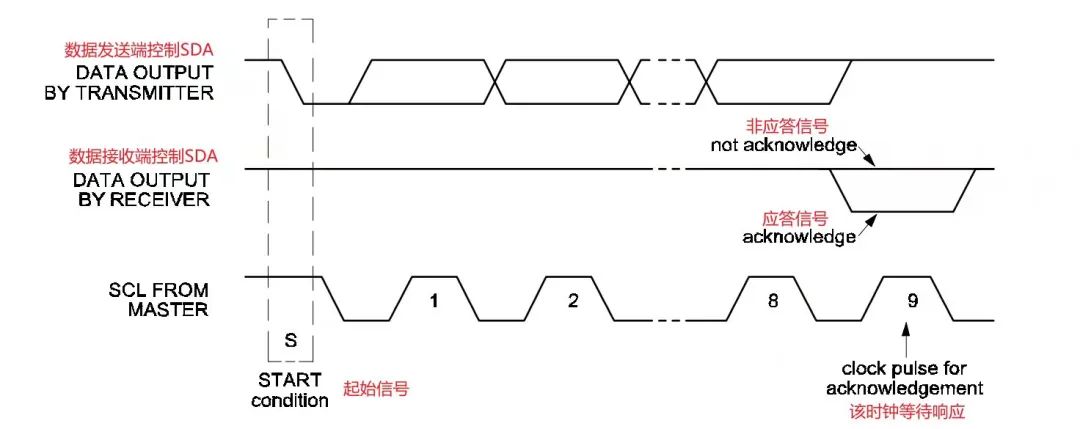
常说的I2C协议是干啥的(电子硬件)
I2C(Inter-Integrated circuit)协议是电子传输信号中常用的一种协议。 它是一种两线式串行双向总线,用于连接微控制器和外部设备,也因为它所需的引脚数只需要两条(CLK和DATA),硬件实现简单&…...

C/C++进程超详细详解【中部分】(系统性学习day07)
目录 前言 一、守护进程 1.概念 2.守护进程创建的原理(如图清晰可见) 3.守护进程的实现(代码块) 二、dup和dup2 1,复制文件描述符 2.文件描述符重定向 三、系统日志 1,打开日志 2,向日…...
S型速度曲线轨迹规划(约束条件为速度和位移)
S型速度曲线规划的基础知识可以查看下面这篇博客: 带平滑功能的斜坡函数(多段曲线控温纯S型曲线SCL源代码+完整算法分析)_RXXW_Dor的博客-CSDN博客PLC运动控制基础系列之梯形速度曲线,可以参看下面这篇博客:PLC运动控制基础系列之梯形速度曲线_RXXW_Dor的博客-CSDN博客运…...

从零手搓一个【消息队列】实现数据的硬盘管理和内存管理(线程安全)
文章目录 一、硬盘管理1, 创建 DiskDataCenter 类2, init() 初始化3, 封装交换机4, 封装队列5, 关于绑定6, 关于消息 二、内存管理1, 数据结构的设计2, 创建 MemoryDataCenter 类3, 关于交换机4, 关于队列5, 关于绑定6, 关于消息7, 恢复数据 三、小结 创建 Spring Boot 项目, S…...

自动驾驶中的感知模型:实现安全与智能驾驶的关键
自动驾驶中的感知模型:实现安全与智能驾驶的关键 文章目录 引言感知模型的作用感知模型的技术安全与挑战结论 2023星火培训【专项营】Apollo开发者社区布道师倾力打造,包含PnC、新感知等的全新专项课程上线了。理论与实践相结合,全新的PnC培训…...
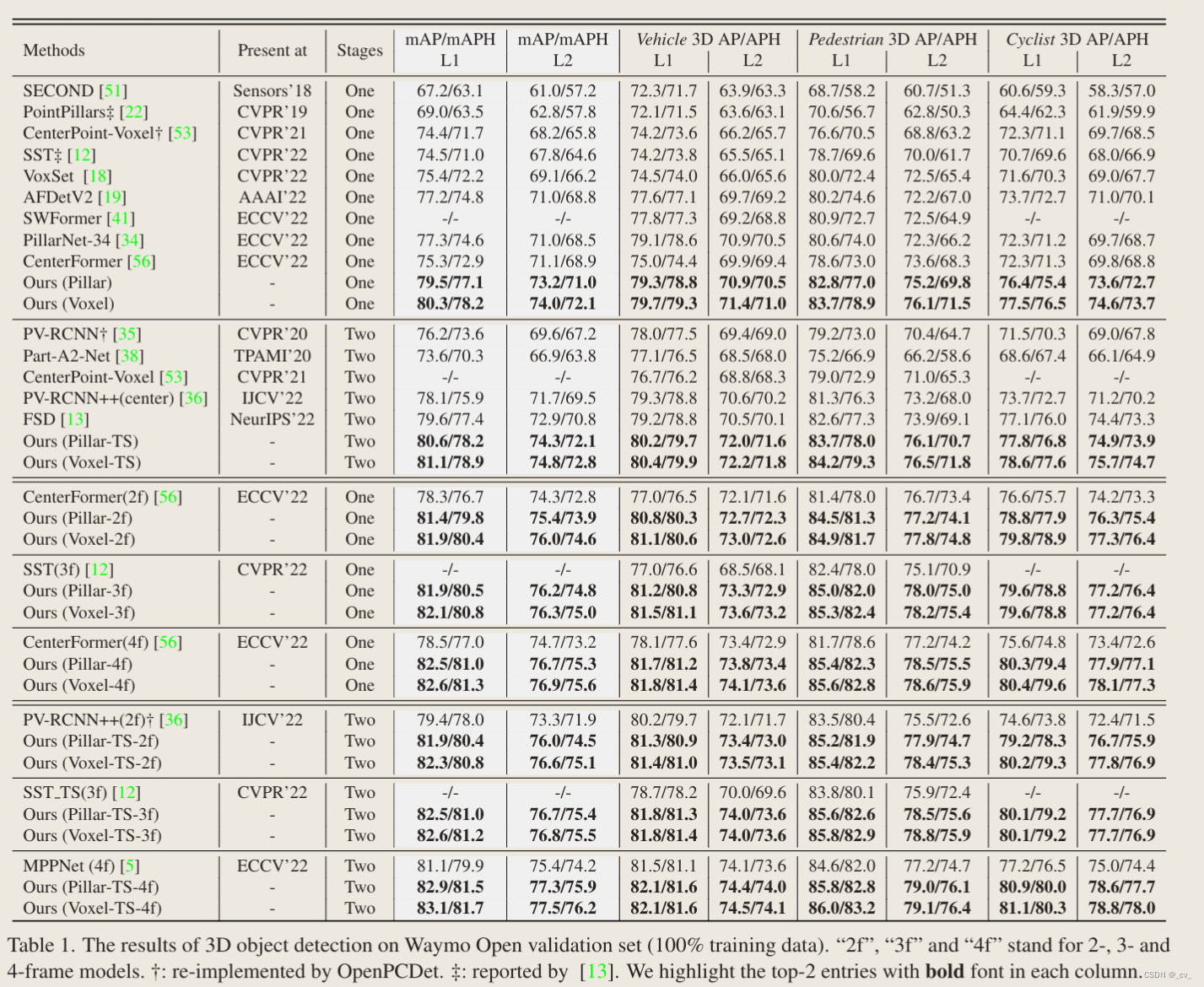
【CVPR 2023】DSVT: Dynamic Sparse Voxel Transformer with Rotated Sets
文章目录 开场白效果意图 重点VoxelNet: End-to-End Learning for Point Cloud Based 3D Object DetectionX-Axis DSVT LayerY-Axis DSVT Layer Dynamic Sparse Window AttentionDynamic set partitionRotated set attention for intra-window feature propagation.Hybrid wind…...

MySQL超入门(1)__迅速上手掌握MySQL
# 1.选择语句 # 注意事项:MySQL不区分大小写,SELECT * 代表选择全部 // 测试一 USE sql_store; -- 使用 sql_store库 SELECT * FROM customers -- 查询customers表 WHERE customer_id 1 OR customer_id 4 -- 条件判断为customer_id 1或customer_id …...
四、浏览器渲染过程,DOM,CSSDOM,渲染,布局,绘制详细介绍
知识点: 1、为什么不能先执行 js文件?? 我们不能先执行JS文件,必须等到CSSOM构建完成了才能执行JS文件,因为前面已经说过渲染树是需要DOM和CSSOM构建完成了以后才能构建,而且JS是可以操控CSS样式的&#…...
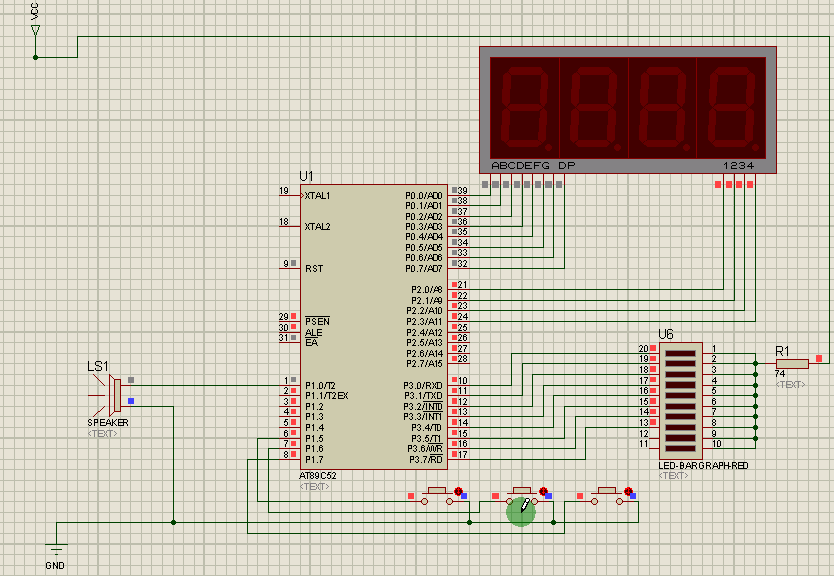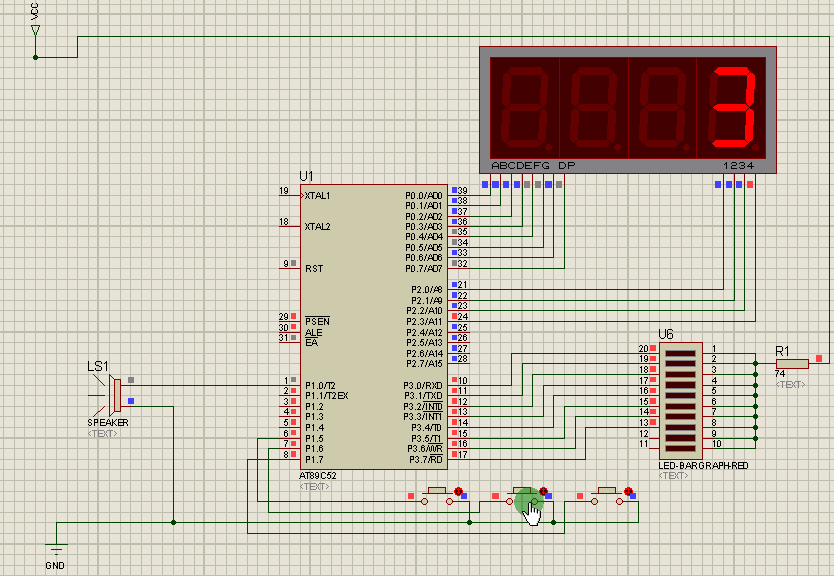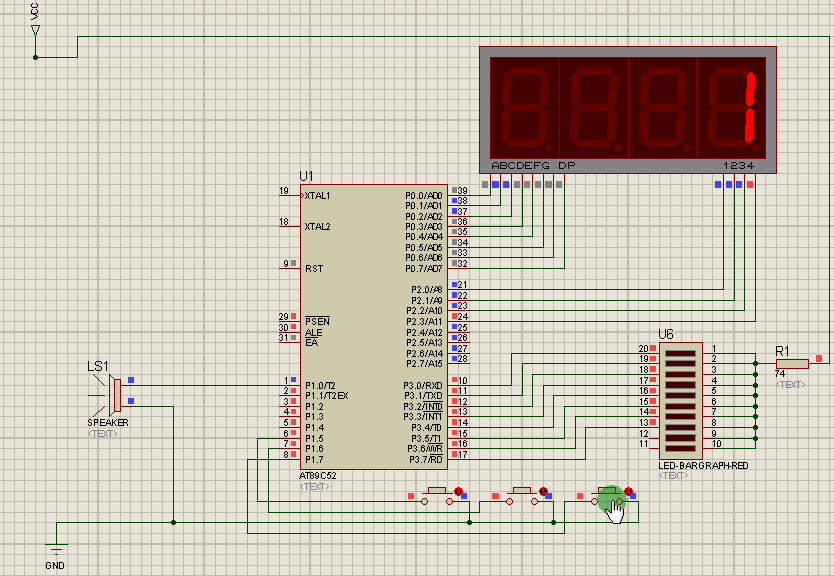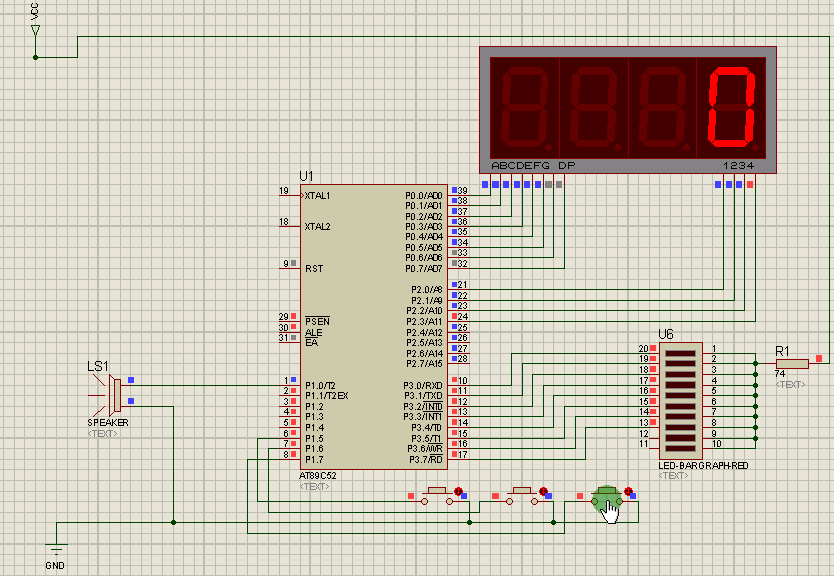
2021-06-10 51单片机设计一个蜂鸣器报警电路每秒
缘由求助一下谢谢啦51单片机_嵌入式-CSDN问答设计一个蜂鸣器报警电路,按下K1,蜂鸣器响一声,按下K2,蜂鸣器响三声,按下K3,蜂鸣器长鸣。要求响声和间隔的时间均为1秒,长鸣不限时,但是此时应设置一…...

D‘Agostino-Pearson正态检验|偏度skewness和峰度kurtosis
DAgostino-Pearson检验(也称为DAgostino和Pearson正态性检验)是一种用于检验数据是否符合正态分布的统计检验方法。它基于数据的样本统计量,主要包括偏度(skewness)和峰度(kurtosis),…...
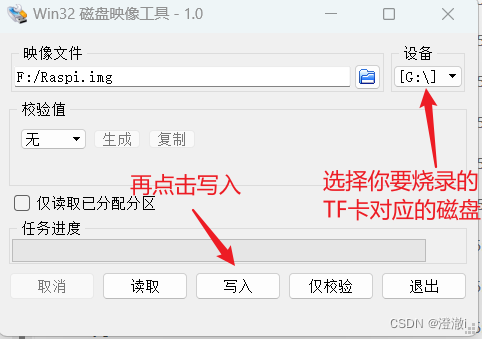
基于树莓派CM4制作img系统镜像批量制作TF卡
文章目录 前言1. 环境与工具2. 制作镜像3. 烧录镜像4. 总结 前言 树莓派烧录完系统做定制化配置比较费时间。在面对大批量的树莓派要配置,那时间成本是非常巨大的。第一次配置完可以说是摸着石头过河,但是会弄了以后再配置,都是一些重复性操…...
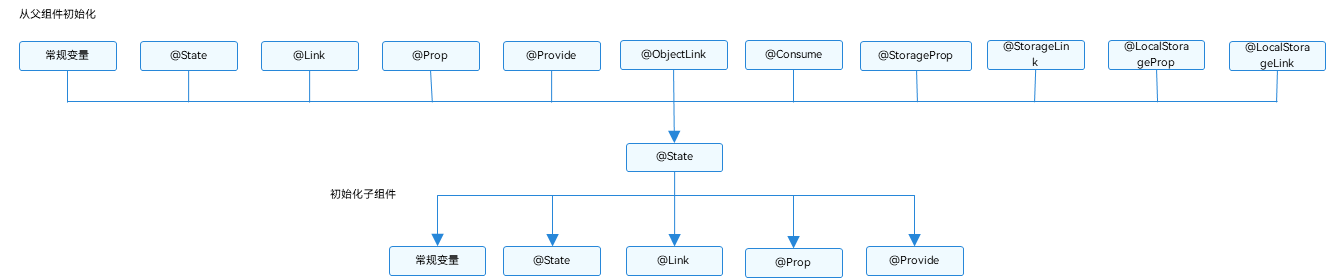
【中秋国庆不断更】OpenHarmony组件内状态变量使用:@State装饰器
State装饰的变量,或称为状态变量,一旦变量拥有了状态属性,就和自定义组件的渲染绑定起来。当状态改变时,UI会发生对应的渲染改变。 在状态变量相关装饰器中,State是最基础的,使变量拥有状态属性的装饰器&am…...

【Java 进阶篇】MySQL多表关系详解
MySQL是一种常用的关系型数据库管理系统,它允许我们创建多个表格,并通过各种方式将这些表格联系在一起。在实际的数据库设计和应用中,多表关系是非常常见的,它能够更好地组织和管理数据,实现数据的复杂查询和分析。本文…...

【开发篇】十、Spring缓存:手机验证码的生成与校验
文章目录 1、缓存2、用HashMap模拟自定义缓存3、SpringBoot提供缓存的使用4、手机验证码案例完善 1、缓存 缓存是一种介于数据永久存储介质与数据应用之间的数据临时存储介质使用缓存可以有效的减少低速数据读取过程的次数(例如磁盘IO),提高…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
