OpenCV实现模板匹配和霍夫线检测,霍夫圆检测
一,模板匹配




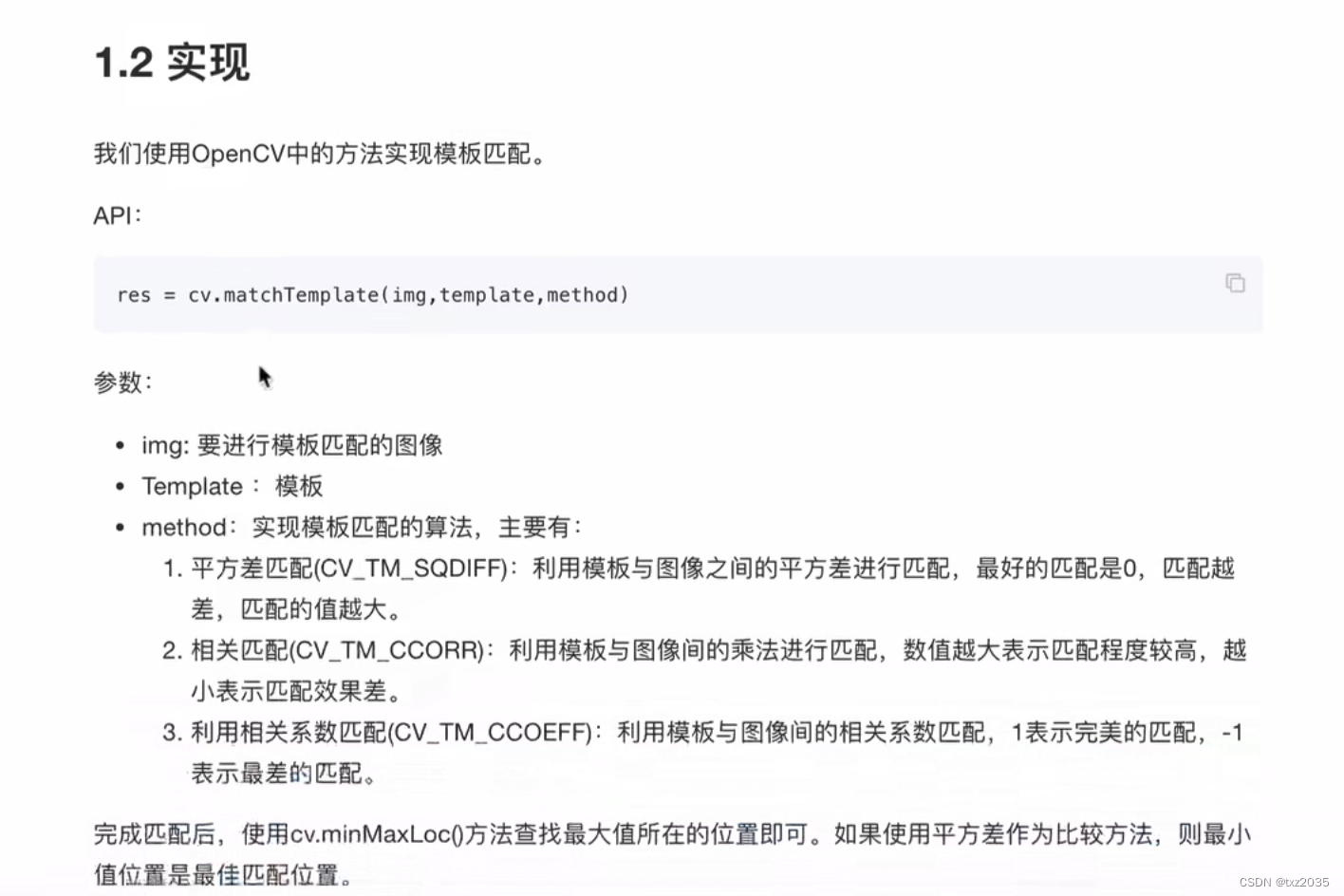

1.1代码实现
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei']#图像和模板的读取
img = cv.imread("cat.png")
template = cv.imread(r"E:\All_in\opencv\cat_1.png")
h,w,l = template.shape #template.shape 返回模板图像的高度、宽度和通道数。#模板匹配
res = cv.matchTemplate(img,template,cv.TM_CCORR) #cv.TM_CCORR 是匹配方法,表示使用相关系数进行匹配。#返回图像中最匹配的位置,确定左上角的坐标,并将匹配位置绘制在图像上
min_val,max_val,min_loc,max_loc = cv.minMaxLoc(res) #cv.minMaxLoc 函数返回匹配结果矩阵中的最小值、最大值及其对应的位置。在这里,我们只关心最大值和其对应的位置。#使用平方差时最小值为最佳匹配位置
#top_left = min_loc
"""确定最佳匹配位置的左上角坐标(top_left)和
右下角坐标(bottom_right),并在图像上绘制矩形框来表示匹配位置:"""
top_left = max_loc
bottom_right = (top_left[0] + w,top_left[1] + h)
cv.rectangle(img , top_left,bottom_right,(0,255,0),5)
"""top_left 和 bottom_right 分别是矩形框的左上角和右下角坐标,
(0, 255, 0) 是矩形框的颜色,(0, 255, 0) 表示绿色,2 是矩形框的线宽。"""#图像显示
plt.imshow(img[:,:,::-1])
plt.title('匹配结果'),plt.xticks([]),plt.yticks([])
plt.show()1.2效果展示

二,霍夫线变换
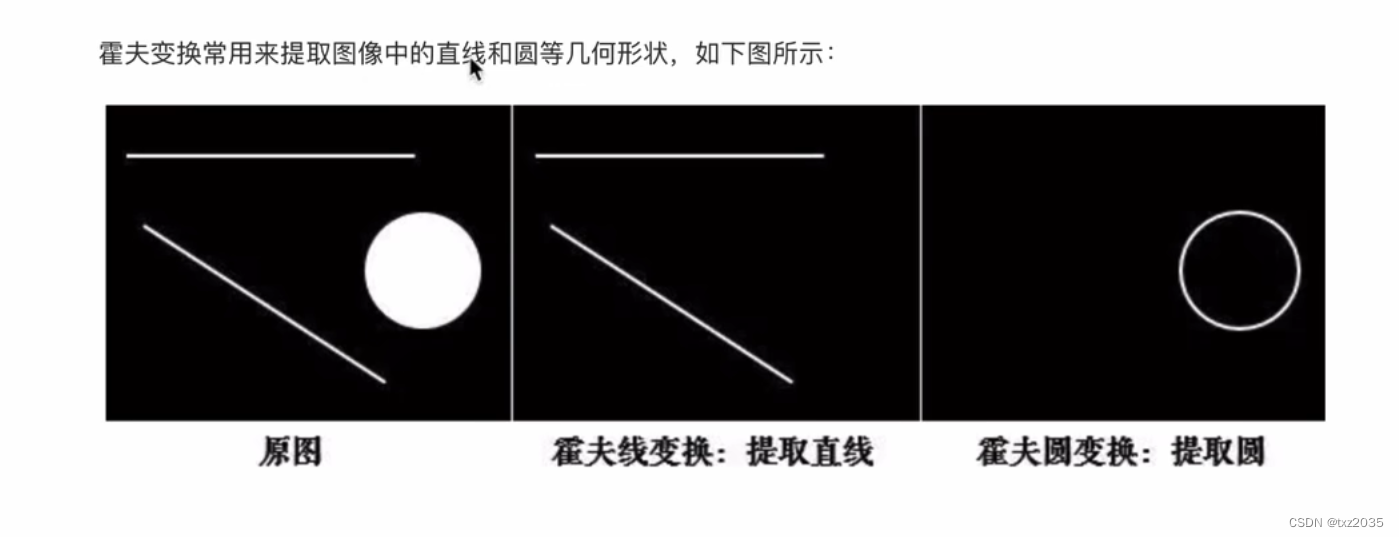

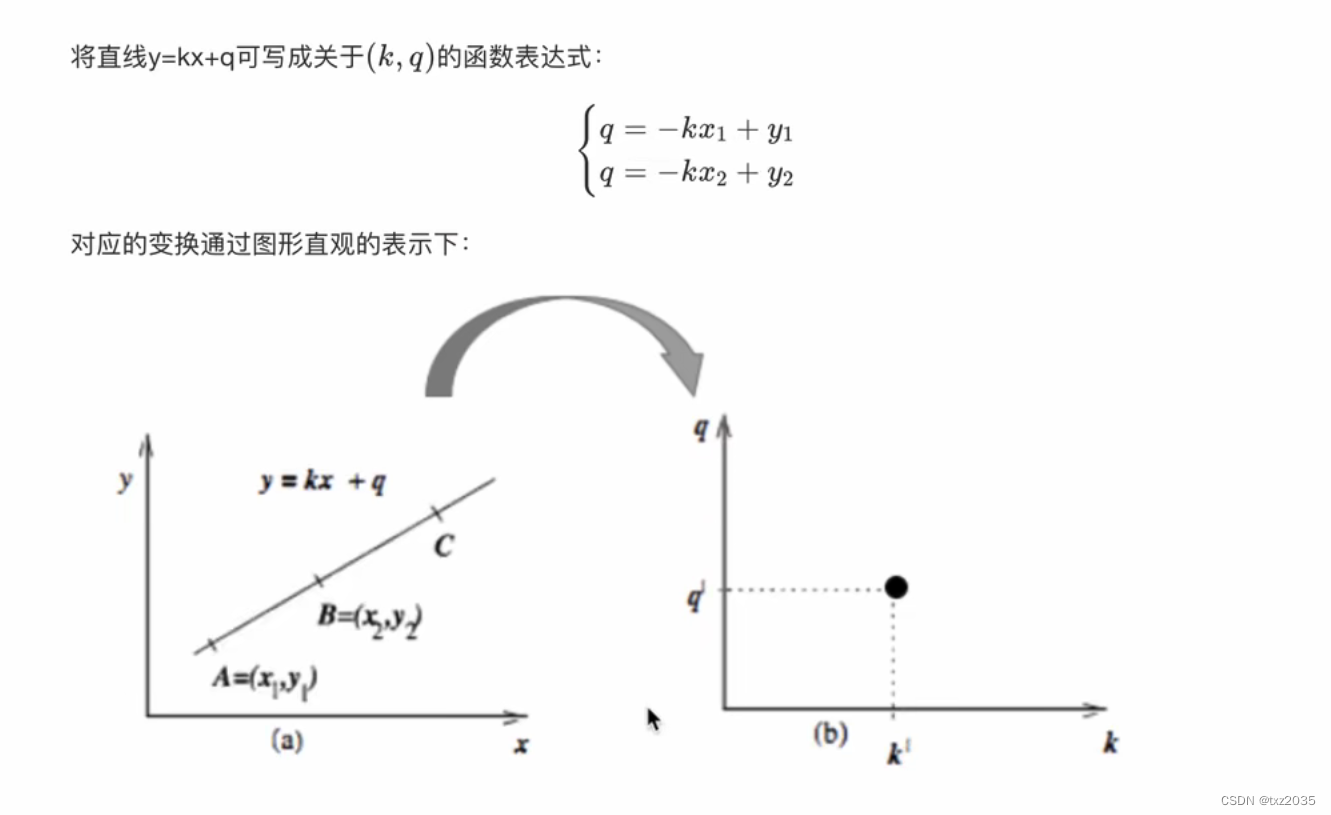


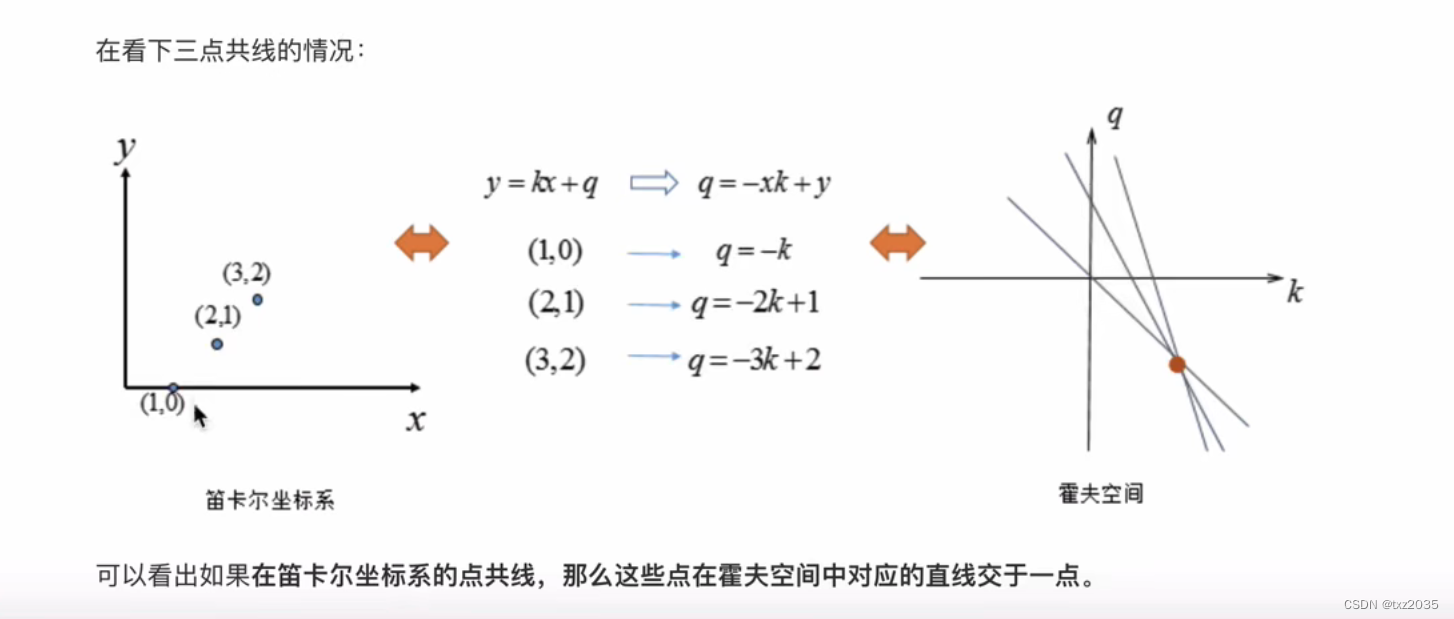

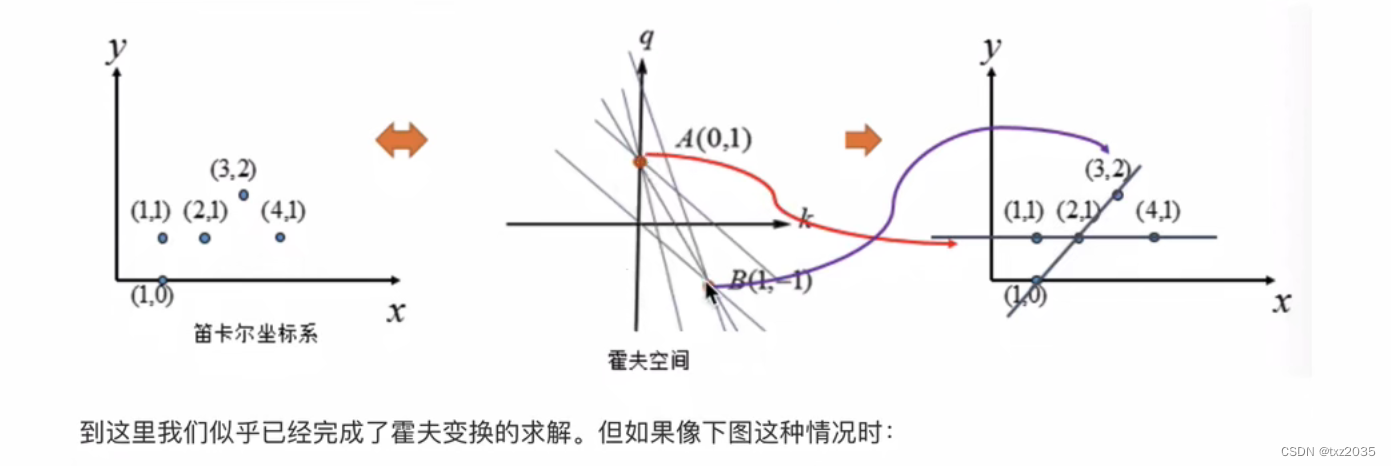

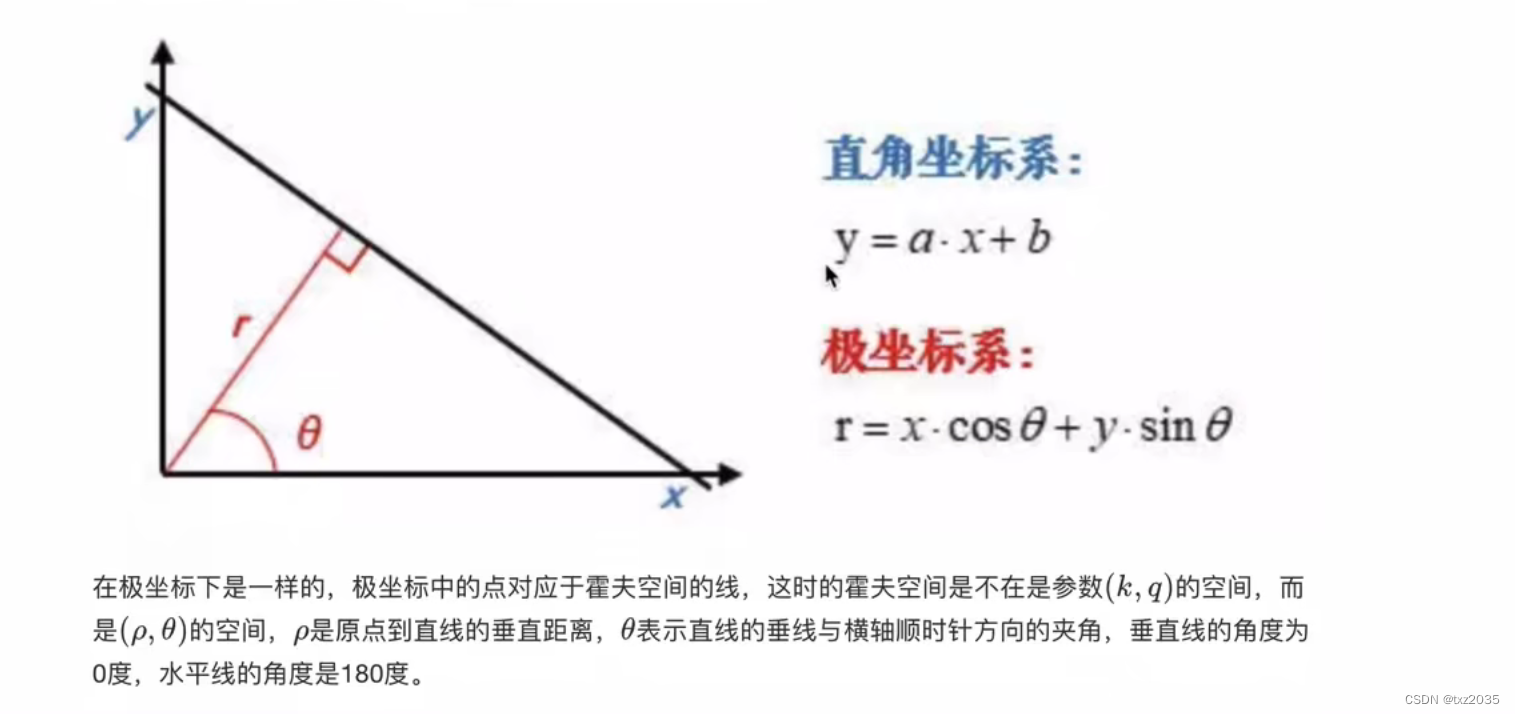
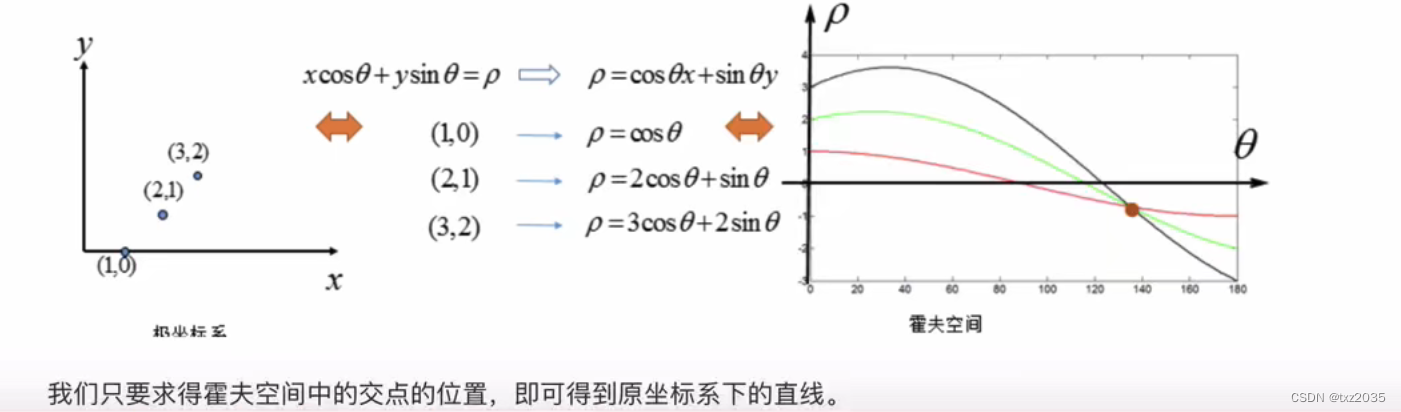



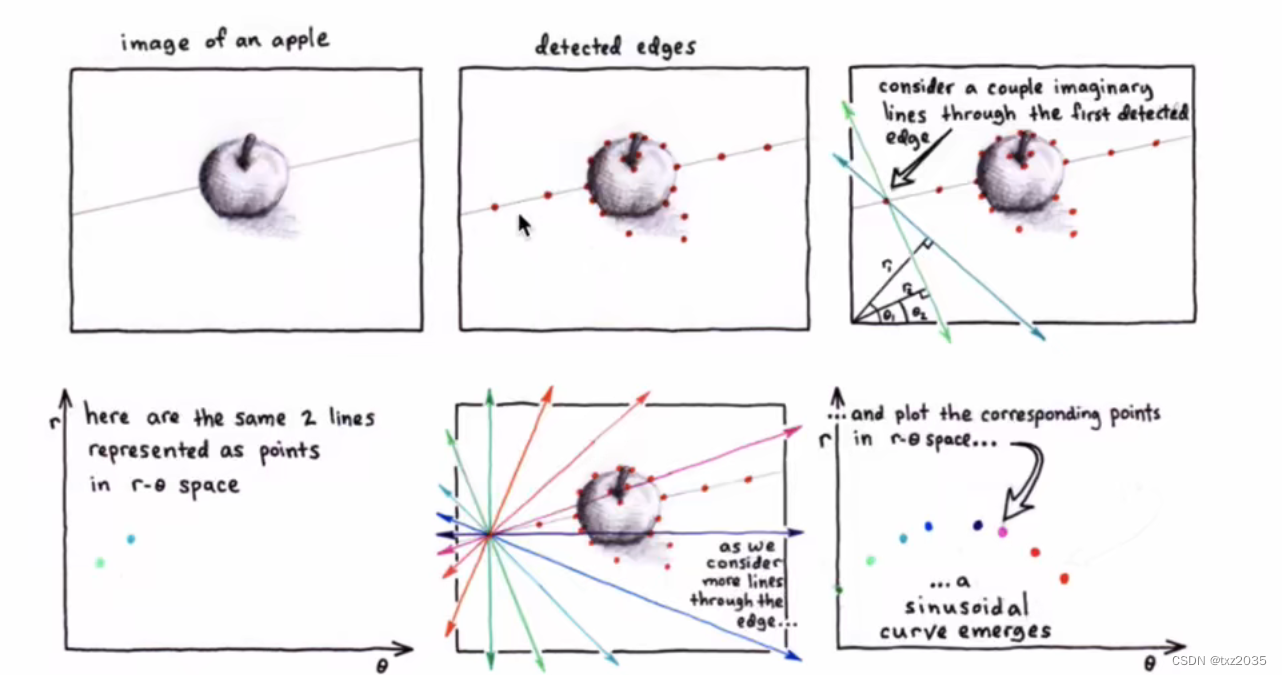

2.1代码实现
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei']#加载图片,转为二值图
img = cv.imread("line.png")gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray,50,150)
'''
50 和 150:Canny 边缘检测的阈值参数。这两个参数用于控制边缘的检测灵敏度
使用 cv.cvtColor() 函数将图像从 BGR 格式转换为灰度图像,并将结果存储在变量 gray 中。
再利用 cv.Canny() 函数对灰度图像进行边缘检测,得到边缘图像并将其存储在变量 edges 中
'''#霍夫直线变换
lines = cv.HoughLines(edges,0.8,np.pi / 180,150)
'''0.8:距离精度 rho 的值,表示极坐标距离 rho 的最小步长。
np.pi / 180:角度精度 theta 的值,表示极坐标角度 theta 的最小步长。
150:阈值,表示在霍夫空间中检测直线时所需的最低投票数。投票数高于阈值的直线将被认为是有效的直线。
'''#将检测的线绘制在图像上(极坐标)
for line in lines:rho,theta = line[00]a = np.cos(theta)b = np.sin(theta)x0 = a * rhoy0 = b * rhox1 = int(x0 + 1000 * (-b))y1 = int(y0 + 1000 * (a))x2 = int(x0 - 1000 * (-b))y2 = int(y0 - 1000 *(a))cv.line(img , (x1,y1),(x2,y2),(0,255,0))
'''遍历检测到的直线参数列表 lines。对于每条直线,首先获取直线的极坐标参数 rho 和 theta。
然后,根据极坐标中的角度 theta 计算出直线的斜率参数 a 和 b。
再根据极坐标中的距离 rho 计算出直线上的一对坐标 (x0, y0)。
接下来,利用斜率和距离计算直线上另外两个点的坐标 (x1, y1) 和 (x2, y2)。
最后,使用 cv.line() 函数在原始图像 img 上绘制检测到的直线,线段颜色为绿色。
'''
#图像显示
plt.figure(figsize=(5,4),dpi=100)
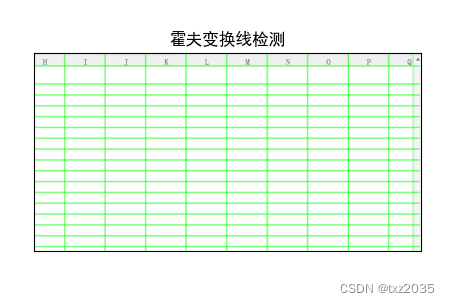
plt.imshow(img[:,:,::-1]),plt.title("霍夫变换线检测")
plt.xticks([]),plt.yticks([])
plt.show()2.2结果展示
三,霍夫圆检测




3.1代码实现
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei']#读取图像转化为灰度图
planets = cv.imread("circle.png")
gray_img = cv.cvtColor(planets,cv.COLOR_BGR2GRAY)#进行模糊去噪点
img = cv.medianBlur(gray_img,7)#霍夫圆检测
circles = cv.HoughCircles(img , cv.HOUGH_GRADIENT,1,200,param1=100,param2=30,minRadius=0,maxRadius=100)# 判断是否成功找到圆
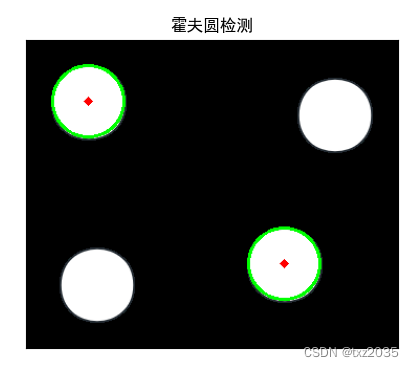
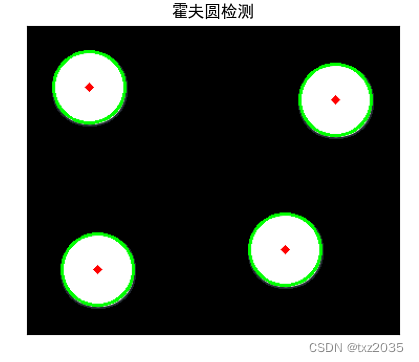
if circles is not None:# 将结果显示在图像上for i in circles[0, :]:cv.circle(planets, (i[0], i[1]), i[2], (0, 255, 0), 2) # 绘制圆形cv.circle(planets, (i[0], i[1]), 2, (0, 0, 255), 3) # 绘制圆心# 图像显示plt.figure(figsize=(5, 4), dpi=100)plt.imshow(planets[:, :, ::-1])plt.title("霍夫圆检测")plt.xticks([])plt.yticks([])plt.show()
else:print("未检测到圆")3.2结果展示
](https://img-blog.csdnimg.cn/237111d87e9c48f68e038d75a72d4af6.png)
相关文章:
OpenCV实现模板匹配和霍夫线检测,霍夫圆检测
一,模板匹配 1.1代码实现 import cv2 as cv import numpy as np import matplotlib.pyplot as plt from pylab import mplmpl.rcParams[font.sans-serif] [SimHei]#图像和模板的读取 img cv.imread("cat.png") template cv.imread(r"E:\All_in\o…...

消息队列实现进程之间通信方式
1. snd 源代码 #include <myhead.h>#define ERR_MSG(msg) do{\fprintf(stderr,"__%d__:",__LINE__);\perror(msg);\ }while(0)typedef struct{ long msgtype; //消息类型char data[1024]; //消息正文 }Msg;#define SIZE sizeof(Msg)-sizeof(long)int main(i…...

用简单例子讲清楚webgl模板测试
文章目录 搭建简易的webgl环境绘制简单三角形(不带stencilTest)绘制另一个三角形(不带模板测试)加入模板测试总结调参练习 搭建简易的webgl环境 一直以来,我只是想通过搭建纯webgl环境,进行开发,来清楚地了…...
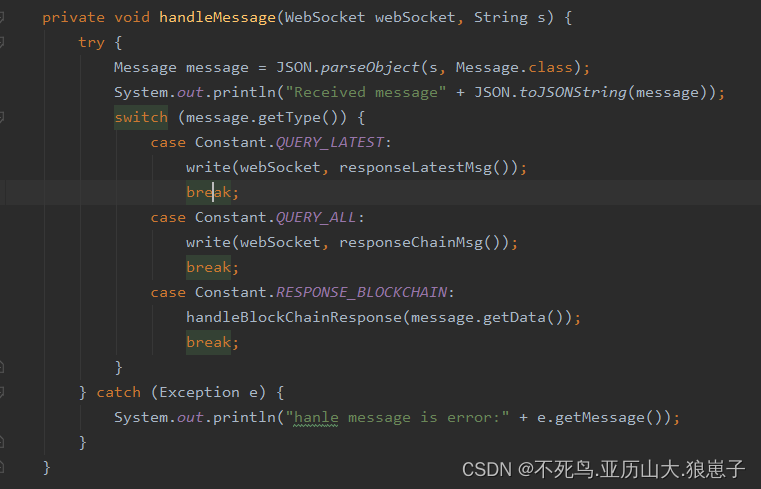
区块链(8):p2p去中心化之websoket服务端实现业务逻辑
1 业务逻辑 例如 peer1和peer2之间相互通信 peer1通过onopen{ write(Mesage(QUERY_LATEST))} 向peer2发送消息“我要最新的区块”。 peer2通过onMessage收到消息,通过handleMessage方法对消息进行处理。 handleMessage根据消息类型进行处理 RESPONSE_BLOCKCHAIN:返回区块链…...

composer安装与设置
1、到官网下载 composer.phar。下载地址:Composer 2、将下载的composer.phar 复制到 composer 文件夹中 3、在composer文件夹中新建文件 composer.bat,内容为 php "%~dp0composer.phar" %* 5、设置环境变量的path,添加composer文件夹...

unordered_map/unordered_set的学习[unordered系列]
文章目录 1.老生常谈_遍历2.性能测试3.OJ训练3.1存在重复元素3.2两个数组的交集Ⅱ3.3两句话中的不常见单词3.4两个数组的交集3.5在长度2N的数组中找出重复N次的元素 1.老生常谈_遍历 #pragma once #define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <l…...

C++位图—布隆过滤器
目录 位图概念位图应用 布隆过滤器简介布隆过滤器的优缺点布隆过滤器应用场景布隆过滤器实现布隆过滤器误判率分析 总结 位图概念 位图是一种数据结构,用于表示一组元素的存在或不存在,通常用于大规模数据集的快速查询。它基于一个位数组(或位…...

SQL SELECT 语句进阶
之前探讨了SQL SELECT 语句的基础内容,包括语法、字段选择、记录限制和数据源指定。今天将进一步深入,探讨多表连接、过滤结果集和逻辑运算等高级主题,还有LIKE 模糊查询、ORDER BY 对结果集排序、运用聚合函数汇总结果以及 GROUP BY 子句与相关应用。 本文将继续使用《三国…...
Mac程序坞美化工具 uBar
uBar是一款为Mac用户设计的任务栏增强软件,它可以为您提供更高效和更个性化的任务管理体验。 以下是uBar的一些主要特点和功能: 更直观的任务管理:uBar改变了Mac上传统的任务栏设计,将所有打开的应用程序以类似于Windows任务栏的方…...
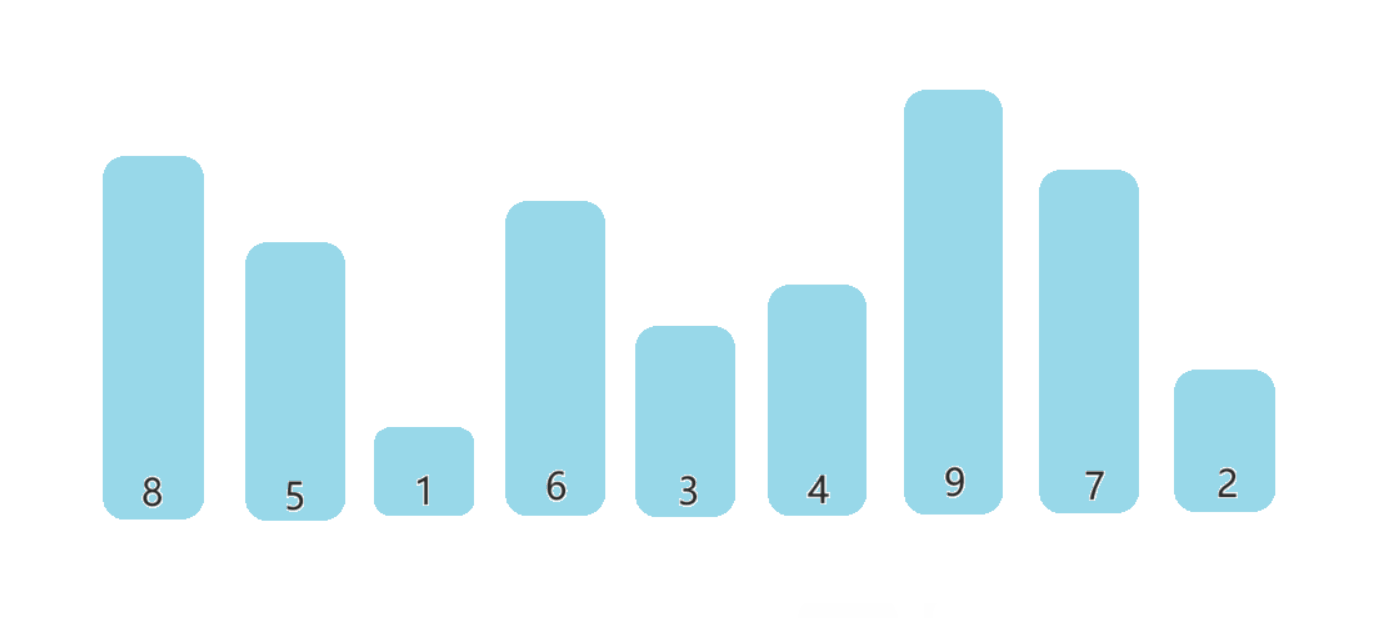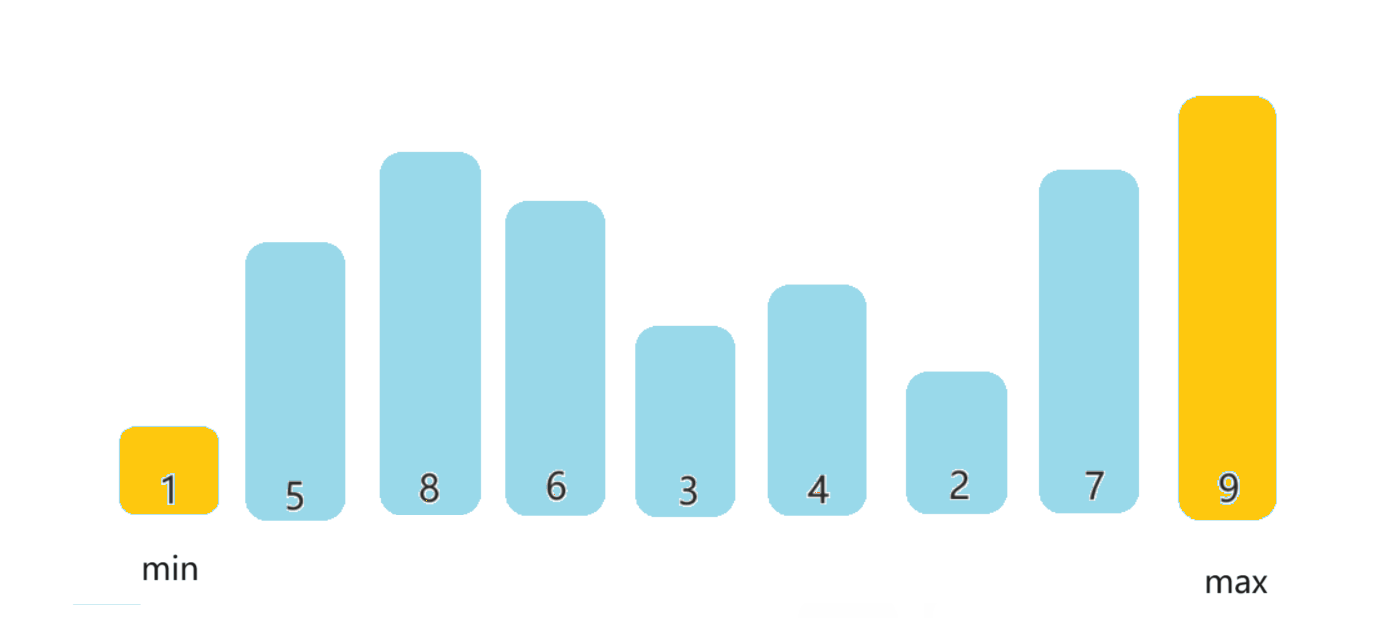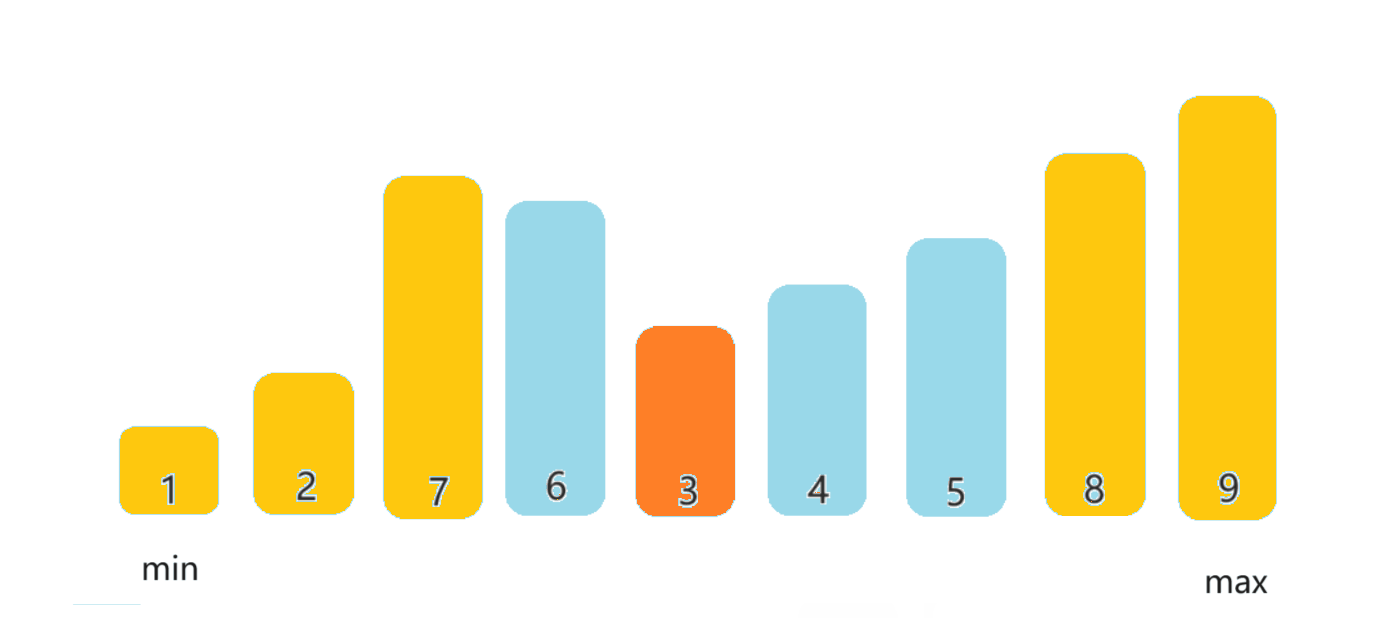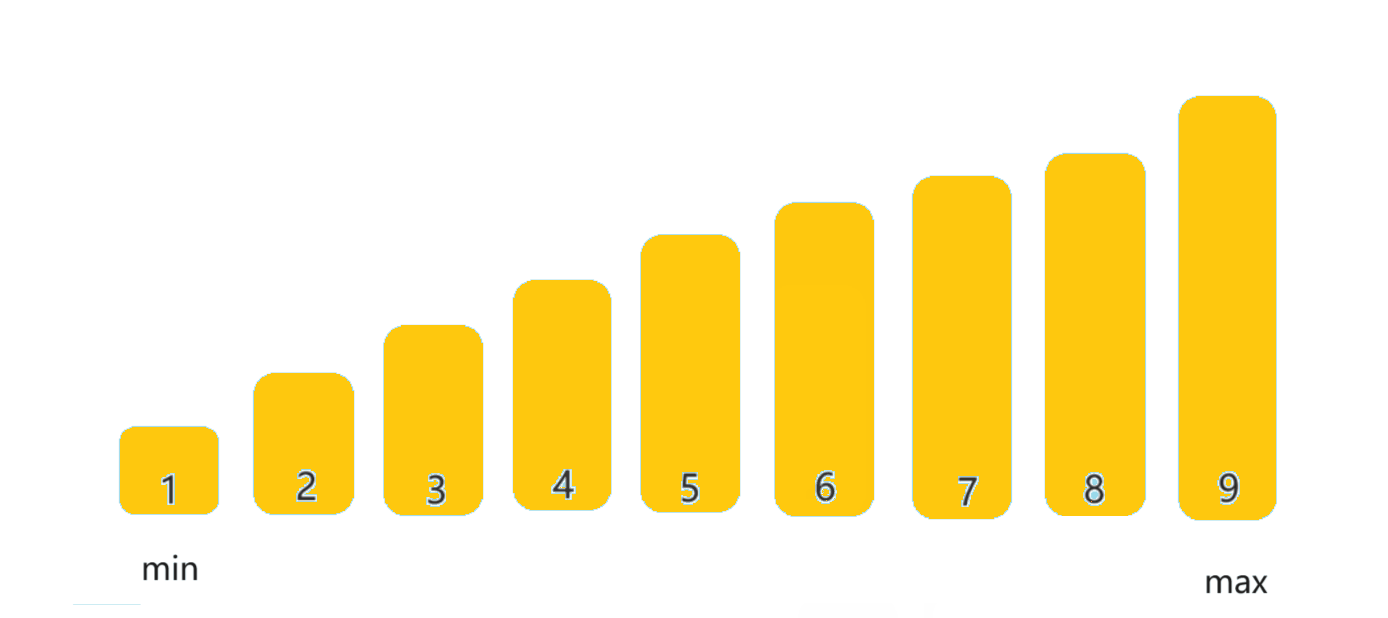
【数据结构】排序之插入排序和选择排序
🔥博客主页:小王又困了 📚系列专栏:数据结构 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、排序的概念及其分类 📒1.1排序的概念 📒1.2排序…...

6.html表单
HTML表单(HTML form)是网页中用于收集用户输入数据的一种方式。表单由多个表单元素组成,通常包括输入框,复选框,单选按钮,下拉列表和提交按钮等。 HTML表单元素的基本结构如下: <form acti…...

【python学习第11节:numpy】
文章目录 一,numpy(上)1.1基础概念1.2数组的属性1.3数组创建1.4 类型转换1.5ndarry基础运算(上)矢量化运算1.6拷贝和视图1.6.1完全不复制1.6.2视图或浅拷贝1.6.3深拷贝 1.7索引,切片和迭代1.7.1一维数组1.7…...

Eclipse 主网即将上线迎空投预期,Zepoch 节点或成受益者?
目前,Zepoch 节点空投页面中,模块化 Layer2 Rollup 项目 Eclipse 出现在其空投列表中。 配合近期 Eclipse 宣布了其将由 SVM 提供支持的 Layer2 主网架构,并将在今年年底上线主网的消息后,不免引发两点猜测:一个是 Ecl…...
 | 输入输出)
JavaSE | 初识Java(四) | 输入输出
基本语法 System.out.println(msg); // 输出一个字符串, 带换行 System.out.print(msg); // 输出一个字符串, 不带换行 System.out.printf(format, msg); // 格式化输出 println 输出的内容自带 \n, print 不带 \n printf 的格式化输出方式和 C 语言的 printf 是基本一致的 代码…...

车牌超分辨率:License Plate Super-Resolution Using Diffusion Models
论文作者:Sawsan AlHalawani,Bilel Benjdira,Adel Ammar,Anis Koubaa,Anas M. Ali 作者单位:Prince Sultan University 论文链接:http://arxiv.org/abs/2309.12506v1 内容简介: 1)方向:图像超分辨率技术…...
如何制作在线流程图?6款在线工具帮你轻松搞定
流程图,顾名思义 —— 用视觉化的方式来描述一种过程或流程。它可以应用于各种领域,从业务流程,算法,到计算机程序等。然而,在创建流程图时,可能会遇到许多问题或者困惑,如缺乏专业的设计技能&a…...

反SSDTHOOK的另一种思路-0环实现自己的系统调用
反SSDTHOOK的另一种思路-0环实现自己的系统调用 大家都知道我们在应用层使用系统api除了gdi相关的都会走中断门或者systementer进0环然后在走ssdt表去执行0环的函数 这也就导致了ssdthook可以挡下大部分的api调用,那如果我们进0环走另外一条路线的话不通过ssdt就可…...
)
Certbot签发和续费泛域名SSL证书(通过DNS TXT记录来验证域名有效性)
我们在使用let’s encrypt获取免费的HTTPS证书的时候,let’s encrypt需要对域名进行验证,以确保域名是你自己的 之前用默认的文件验证方式总有奇怪的问题导致失败,我也是很无奈,于是改用验证DNS-TXT记录的方式来验证,而…...

PY32F003F18之RTC
一、RTC振荡器 PY32F003F18实时时钟的振荡器是内部RC振荡器,频率为32.768KHz。它也可以使用HSE时钟,不建议使用。HAL库提到LSE振荡器,但PY32F003F18实际上没有这个振荡器。 缺点:CPU掉电后,需要重新配置RTCÿ…...

redis主从从,redis-7.0.13
redis主从从,redis-7.0.13 下载redis安装redis安装redis-7.0.13过程报错1、没有gcc,报错2、没有python3,报错3、[adlist.o] 错误 127 解决安装报错安装完成 部署redis 主从从结构redis主服务器配置redis启动redis登录redisredis默认是主 redi…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...
