2023湖南省赛游记/题解
省赛拖了大哥们的后腿,感觉随便补个正常一队水平的人,我们一队肯定能AK。只能说自己真的菜,全程帮不上什么忙,还负贡献,真的想笑
B
暴力sg
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr int N=1e6;
int sg[N+5];
int vis[N+5];
void getsg(){for (int i=1;i<=N;i++){// vis[sg[i-1]]=i;int res=sqrt(1.0*i);if (i==res*res){for (int k=1;k<=res;k++){vis[sg[i-(i-res*res+k*res)]]=i;}}else{for (int k=0;k<=res;k++){vis[sg[i-(i-res*res+k*res)]]=i;}}while (vis[sg[i]]==i){sg[i]++;}}
}
void yrzr(){getsg();int n;std::cin>>n;int sum=0;for (int i=1;i<=n;i++){int x;std::cin>>x;sum^=sg[x];}if (sum){std::cout<<"First\n";}else{std::cout<<"Second\n";}
}
D
大哥赛后说是HN省选dp原题(见状压dp P3188 [HNOI2007] 梦幻岛宝珠),然后这个题比那个题范围还要大,看完题解发现是贪心题,但是还是按位分组的思想去解决问题
首先对于一个目标物品来说,它的需求可以表示为几个二进制位的组合,然后我们分解每一个目标物品到位上,然后将其按位合并,最后可以表示为一个二进制串(用数组表示)
然后对于每一件物品,重量小的物品可以合并成大物品,但大物品不能拆解成小物品,所以我们按位从小到大枚举目标物品数组,贪心地用小物品去满足当前位的数量,然后将剩下的物品贪心地两两合并成下一位的物品。
简要的说就是:目标物品总体可以表示为一个数组,然后拥有的物品贪心从小到大去填补目标重量
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr int inf=1e9;
std::priority_queue<int,std::vector<int>,std::greater<int>> q[5105];
void yrzr(){int n;std::cin>>n;for (int i=1;i<=n;i++){int x,y;std::cin>>x>>y;q[x].push(y);}int m;std::cin>>m;std::vector<int> sum(5105);while (m--){int t,h;std::cin>>t>>h;while (h){if (h&1) sum[t]++;h>>=1;t++;}}for (int i=0;i<=5100;i++){if (sum[i]>=2){int temp=sum[i],p=i;sum[i]=0;while (temp){if (temp&1) sum[p]++;temp>>=1;p++;}}}int ans=0;for (int i=0;i<=5100;i++){if (q[i].size()<sum[i]){std::cout<<"-1\n";return;}for (int j=1;j<=sum[i];j++){ans+=q[i].top();q[i].pop();}while (q[i].size()>=2){int temp=q[i].top();q[i].pop();temp+=q[i].top();q[i].pop();q[i+1].push(temp);}}std::cout<<ans;
}
F
图论题,首先Floyed求出一个字母变成另一个字母的最小花费,然后对于两个不同的字母,暴力预处理出他们变成同样字母的最小花费。最后A串不动,枚举B串位置,求最小即可
可能有重边,输入时 d i s dis dis取最小
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
constexpr int inf=1e16;
void yrzr(){int n,m;std::cin>>n>>m;std::vector<int> a(n),b(n);for (int i=0;i<n;i++){std::cin>>a[i];}for (int i=0;i<n;i++){std::cin>>b[i];}std::vector<std::vector<int>> dis(405,std::vector<int>(405,inf)),c(405,std::vector<int>(405,inf));for (int i=1;i<=m;i++){int x,y,z;std::cin>>x>>y>>z;dis[x][y]=std::min(dis[x][y],z);}for (int i=1;i<=400;i++){dis[i][i]=c[i][i]=0;}for (int k=1;k<=400;k++){for (int i=1;i<=400;i++){for (int j=1;j<=400;j++){dis[i][j]=std::min(dis[i][j],dis[i][k]+dis[k][j]);}}}for (int i=1;i<=400;i++){for (int j=1;j<=400;j++){for (int k=1;k<=400;k++){c[i][j]=std::min(c[i][j],dis[i][k]+dis[j][k]);}}}int ans=inf;for (int i=0;i<n;i++){int sum=0;bool ok=1;for (int j=0;j<n;j++){if (c[a[j]][b[(j+i)%n]]==inf){ok=0;break;}else{sum+=c[a[j]][b[(j+i)%n]];}}if (ok){ans=std::min(ans,sum);}}if (ans==inf){std::cout<<"-1\n";}else{std::cout<<ans<<"\n";}
}
I
数位dp,不知道省赛脑子犯了什么抽,受前几天一道数位dp,直接把状态数组压入map暴力记忆化的影响,想当然的觉得这题也是这么做,大哥直接提出时间复杂度是不够的。后面大哥们说是数位dp加个容斥。
补题的时候也一直在想数位dp+容斥,发现自己容斥不出来(容斥见识的得太少了),看了题解后发现只要一个数位dp就可以了
突然发现这题的思想其实跟前几天做的数位dp是一样的,甚至状态更简单,我们最重要的状态其实就只有当前位第几位,然后还要知道现在有多少个不同的数,这就足够了。因为对于这10个数字来说,后面的数字它只有两种身份,之前选了/没选,所以当前位相同,之前不同的数字个数相同,剩下的方案数就相同,就可以用记忆化。(赛时真的蠢傻了,这种套路思想学数位dp的时候见过很多了)
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr ll mod=1e9+7;
ll f[200005][12][2][2];
int now[12];
void yrzr(){int n;std::cin>>n;std::vector<int> a(n+1),b(n+1);for (int i=1;i<=n;i++){char ch;std::cin>>ch;a[i]=ch-'0';}for (int i=1;i<=n;i++){char ch;std::cin>>ch;b[i]=ch-'0';}reverse(a.begin()+1,a.end());reverse(b.begin()+1,b.end());int A;std::cin>>A;std::function<ll(int,int,int,int)> dfs=[&](int len,int sum,int dif1,int dif2){if (len==0){return 1LL*(sum==A);}if (sum>A){return 0LL;}if (dif1&&dif2&&f[len][sum][dif1][dif2]){return f[len][sum][dif1][dif2];}int x=(dif1?0:a[len]),y=(dif2?9:b[len]);ll res=0;for (int i=x;i<=y;i++){if (now[i]){now[i]++;res=(res+dfs(len-1,sum,dif1|(a[len]!=i),dif2|(b[len]!=i)))%mod;now[i]--;}else{now[i]++;res=(res+dfs(len-1,sum+1,dif1|(a[len]!=i),dif2|(b[len]!=i)))%mod;now[i]--;}}if (dif1&&dif2) f[len][sum][dif1][dif2]=res;return res;};std::cout<<dfs(n,0,0,0);}
J
分别枚举圆心在三个坐标轴,然后二分圆的半径,接下来考虑怎么check,对于一个点来说,我们去计算出它在球内时,圆心所在的区间,存下区间左右端点和权值(表示是左端点还是右端点),遍历一遍看是否有点满足题意即可
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr int N=1e5+5;
int n;
ll x[N],y[N],z[N];
struct node{double pos;int val;
}a[N<<1];
bool check(double r){int cnt=0;for (int i=1;i<=n;i++){double res=r*r-y[i]*y[i]-z[i]*z[i];if (res<0) continue;res=sqrt(res);a[++cnt]={x[i]-res,1};a[++cnt]={x[i]+res,-1};}std::sort(a+1,a+1+cnt,[&](node i,node j){return i.pos<j.pos;});int sum=0;for (int i=1;i<=cnt;i++){sum+=a[i].val;if (sum>=n/2){return 1;}}cnt=0;for (int i=1;i<=n;i++){double res=r*r-x[i]*x[i]-z[i]*z[i];if (res<0) continue;res=sqrt(res);a[++cnt]={y[i]-res,1};a[++cnt]={y[i]+res,-1};}std::sort(a+1,a+1+cnt,[&](node i,node j){return i.pos<j.pos;});sum=0;for (int i=1;i<=cnt;i++){sum+=a[i].val;if (sum>=n/2){return 1;}}cnt=0;for (int i=1;i<=n;i++){double res=r*r-x[i]*x[i]-y[i]*y[i];if (res<0) continue;res=sqrt(res);a[++cnt]={z[i]-res,1};a[++cnt]={z[i]+res,-1};}std::sort(a+1,a+1+cnt,[&](node i,node j){return i.pos<j.pos;});sum=0;for (int i=1;i<=cnt;i++){sum+=a[i].val;if (sum>=n/2){return 1;}}return 0;
}
void yrzr(){std::cin>>n;for (int i=1;i<=n;i++){std::cin>>x[i]>>y[i]>>z[i];}double l=0,r=1e6;for (int i=0;i<=50;i++){double mid=(l+r)/2;if (check(mid)){r=mid;}else{l=mid;}}std::cout<<std::fixed<<std::setprecision(7)<<l;
}
K
补的时候相成状压了,然后状压+矩阵加速???,发现不会写
然后看了题解知道是容斥了,所以以后对于这种小数据除了状压也有可能是容斥
想到容斥就很好做了,每次直接暴力二进制枚举哪些城市不去,在转移的矩阵和答案矩阵上去掉那些转移点,然后dp矩阵加速即可
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr ll mod=1e9+9;
constexpr int N=25;
struct Matrix{int lenn,lenm;ll a[N][N];Matrix() {memset(a,0,sizeof(a));}Matrix operator*(const Matrix &b)const{if (lenm==b.lenn){Matrix res;res.lenn=lenn;res.lenm=b.lenm;for (int i=1;i<=lenn;i++){for (int j=1;j<=b.lenm;j++){for (int l=1;l<=lenm;l++){res.a[i][j]=(res.a[i][j]+a[i][l]*b.a[l][j]%mod)%mod;}}}return res;}}Matrix operator+(const Matrix &b)const{if (lenn==b.lenn&&lenm==b.lenm){Matrix res;res.lenn=lenn;res.lenm=lenm;for (int i=1;i<=lenn;i++){for (int j=1;j<=lenm;j++){res.a[i][j]=a[i][j]+b.a[i][j];}}return res;}}Matrix operator-(const Matrix &b)const{if (lenn==b.lenn&&lenm==b.lenm){Matrix res;res.lenn=lenn;res.lenm=lenm;for (int i=1;i<=lenn;i++){for (int j=1;j<=lenm;j++){res.a[i][j]=a[i][j]-b.a[i][j];}}return res;}}};
int s[10],n,m,k,d;
int a[25][25];
ll solve(int mask){Matrix e,f,ans;ans.lenn=1;ans.lenm=f.lenn=f.lenm=e.lenn=e.lenm=n;std::vector<int> vis(n+1);for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){e.a[i][j]=a[i][j];}f.a[i][i]=1;ans.a[1][i]=1;}for (int i=1;i<=k;i++){if (mask&(1<<(i-1))){int x=s[i];for (int j=1;j<=n;j++){e.a[x][j]=e.a[j][x]=0;}vis[x]=1;ans.a[1][x]=0;}}int temp=d;while (temp){if (temp&1) f=f*e;e=e*e;temp>>=1;}ans=ans*f;ll sum=0;for (int i=1;i<=n;i++){if (vis[i]) continue;sum=(sum+ans.a[1][i])%mod;}return sum;
}
void yrzr(){std::cin>>n>>m>>k>>d;d--;for (int i=1;i<=k;i++){std::cin>>s[i];}for (int i=1;i<=m;i++){int x,y;std::cin>>x>>y;a[x][y]=a[y][x]=1;}ll ans=0;for (int i=0;i<(1<<k);i++){if (__builtin_popcount(i)&1){ans=(ans-solve(i)+mod)%mod;}else{ans=(ans+solve(i))%mod;}}std::cout<<ans;
}
相关文章:

2023湖南省赛游记/题解
省赛拖了大哥们的后腿,感觉随便补个正常一队水平的人,我们一队肯定能AK。只能说自己真的菜,全程帮不上什么忙,还负贡献,真的想笑 B 暴力sg #include <bits/stdc.h> #define ll long long #define ull unsigned…...

海信电视U8KL使用体验:参数卷,画质技术也独有!
每个家庭成员对电视都有不同需求,如何能做到兼顾?看似需求众口难调,其实一台海信电视就能满足所有啦。 海信电视的参数不仅是最卷的,同时画质技术还是国内独有的,能把这样一台优秀的电视搬回家,无论电影、…...

E. Mishap in Club
题目: 样例1: 输入 --输出 1 样例2: 输入 --- 输出 3 思路: 数学贪心模拟思路,由于不知道在俱乐部的人数和在外面的人数,又要尽可能少的人数,那么定义两个变量,一个是里面的人数 i…...
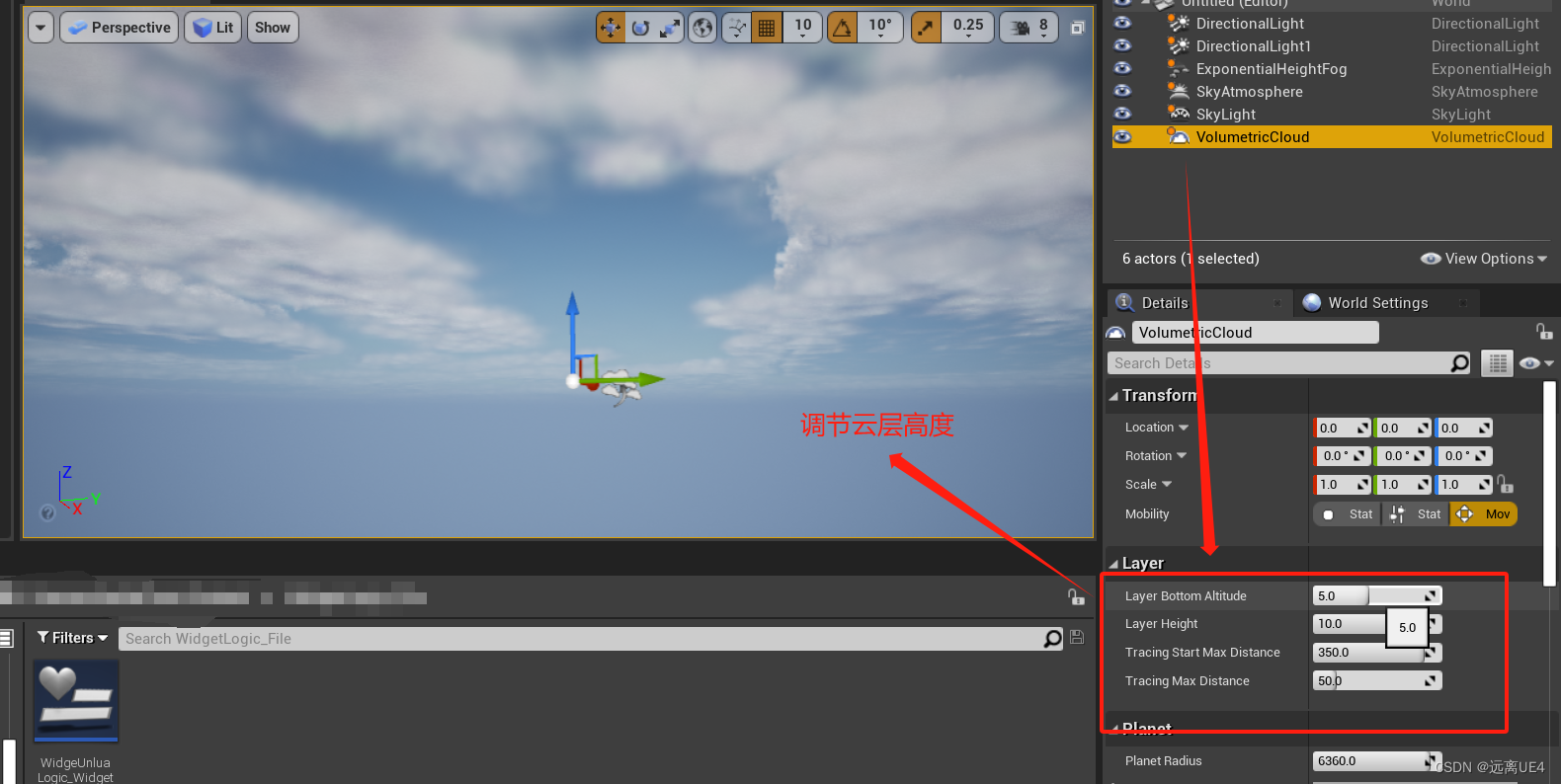
UE4 自带体积云应用
新建空关卡 点击该选项 全部点击一遍 拖进场景...
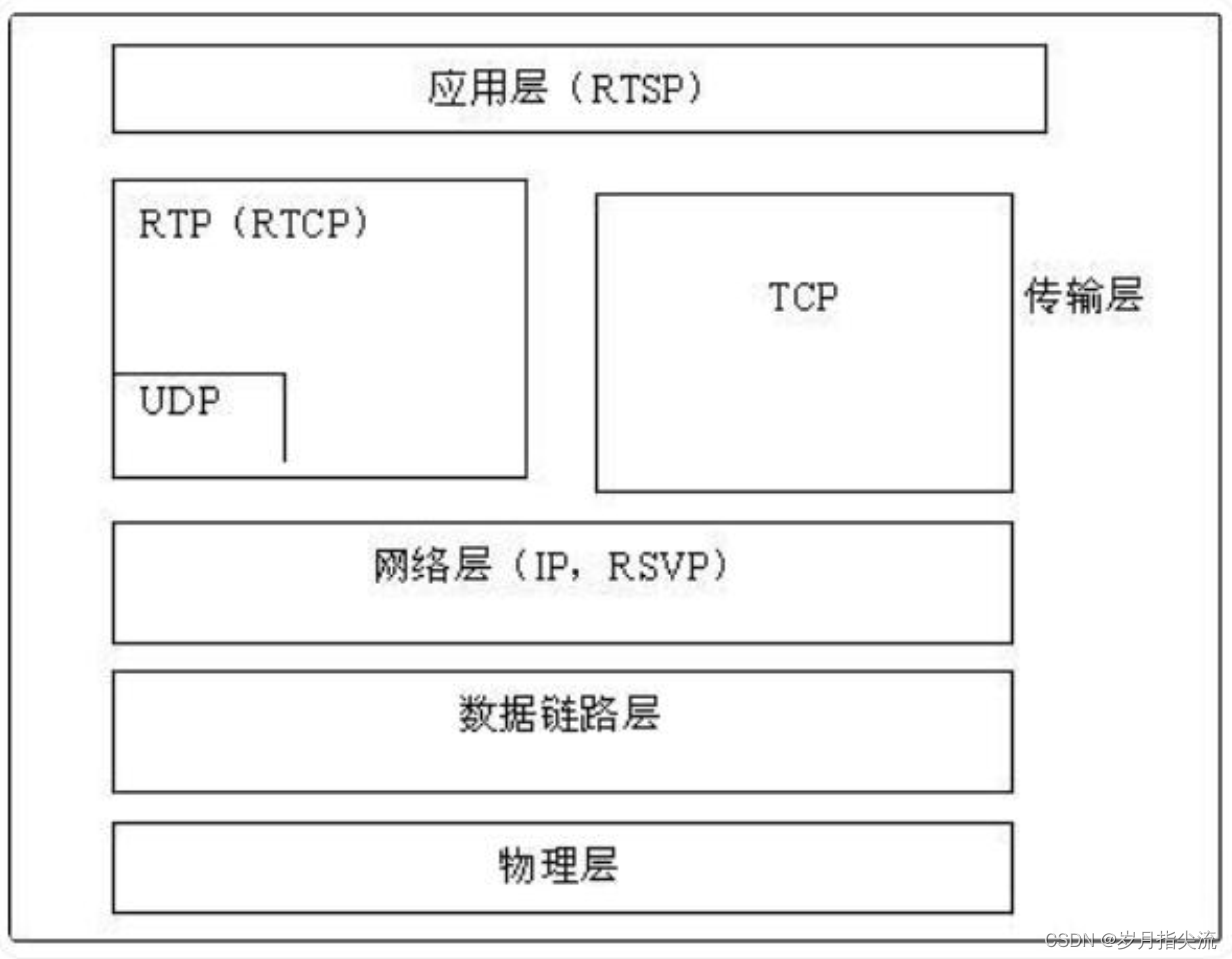
RTP/RTCP 协议讲解
文章目录 前言一、RTP 协议1、RTP 协议概述2、RTP 工作机制3、RTP 协议的报文结构4、wireshark 抓取 RTP 报文 二、RTCP 协议1、RTCP 协议概述2、RTCP 工作机制3、RTCP 数据报4、wireshark 抓取 RTCP 报文 三、RTSP 和 RTP 的关系四、易混淆概念1、RTP over UDP 和 RTP over RT…...

倒计时15天!百度世界2023抢先看
近日消息,在10月17日即将举办的百度世界2023上,百度创始人、董事长兼首席执行官李彦宏将带来主题演讲,“手把手教你做AI原生应用”。 增设社会报名,有机会获得精美伴手礼 目前,百度世界大会已经开放公众参会报名&…...
数据类型和命令(数据类型 二))
Redis 哈希(Hash)数据类型和命令(数据类型 二)
基本概念 Hash是一个键值对的集合,其中每个键都是唯一的。每个键都可以关联多个字段和值,这使得Hash非常适合存储对象或结构化数据。 常用命令 存储、获取、删除:hset、hget、hdel # 添加键为name值为lin hset student name lin # 获取 h…...
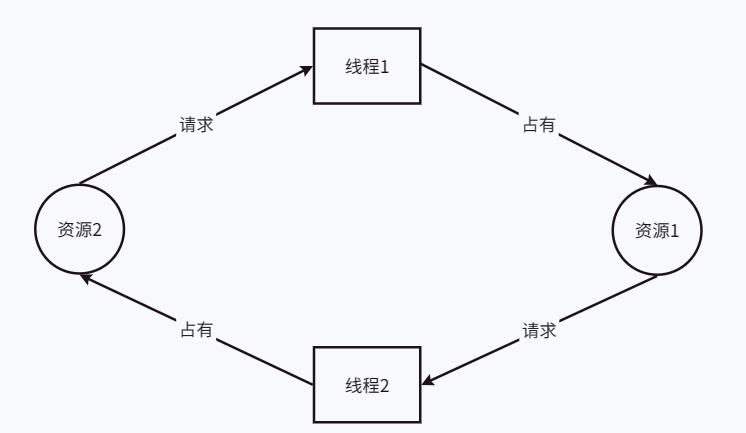
[Linux]线程互斥
[Linux]线程互斥 文章目录 [Linux]线程互斥线程并发访问问题线程互斥控制--加锁pthread_mutex_init函数pthread_mutex_destroy函数pthread_mutex_lock函数pthread_mutex_unlock函数锁相关函数使用示例使用锁的细节加锁解锁的实现原理 线程安全概念常见的线程不安全的情况常见的…...

leetcode-239-滑动窗口最大值
题意描述: 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例: 输入:nums [1,3,-1,…...

基于大语言模型的智能问答系统应该包含哪些环节?
一个完整的基于 LLM 的端到端问答系统,应该包括用户输入检验、问题分流、模型响应、回答质量评估、Prompt 迭代、回归测试,随着规模增大,围绕 Prompt 的版本管理、自动化测试和安全防护也是重要的话题,本篇文章就来探索下这个过程…...

【Cesium创造属于你的地球】相机系统
相机系统里面有setView,flyTo,lookAt,viewBoundingsphere这几种方法,以下是相关的使用方法,学起来!!! setView 该方法可以直接切换相机视口,从而不需要通过一个飞入的效…...

运维困局下确保系统稳定的可行性
业务高速发展背后的困局 随着业务的快速发展,运维体系也逐步的完善起来。业务的稳定性和服务质量也在监控、可用性等体系的相互环抱下健康地成长。所有的问题、故障及影响稳定性的因素都在可控、可收敛的范围内,一切都向着好的方向发展。 这一切的背后…...
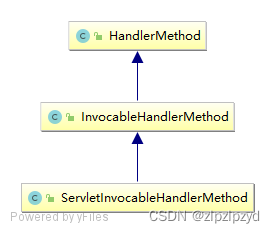
springmvc中DispatcherServlet关键对象
以下代码为 spring boot 2.7.15 中自带的 spring 5.3.29 RequestMappingInfo 请求方法相关信息封装,对应的信息解析在 RequestMappingHandlerMapping 的 createRequestMappingInfo() 中实现。 对于 RequestMapping 赋值的相关信息进行解析 protected RequestMappi…...

某微e-office协同管理系统存在任意文件读取漏洞复现 CNVD-2022-07603
目录 1.漏洞概述 2.影响版本 3.漏洞等级 4.漏洞复现 5.Nuclei自动化扫描POC 某微e-office协同管理系统存在任意文件读取漏洞分析 CNVD-2022-07603https://blog.csdn.net/qq_41490561/article/details/133469649...
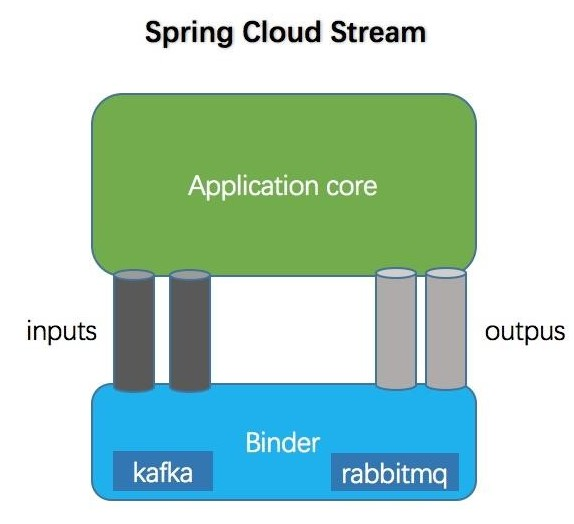
消息驱动 —— SpringCloud Stream
Stream 简介 Spring Cloud Stream 是用于构建消息驱动的微服务应用程序的框架,提供了多种中间件的合理配置 Spring Cloud Stream 包含以下核心概念: Destination Binders:目标绑定器,目标指的是 Kafka 或者 RabbitMQ࿰…...

使用Apache HttpClient爬取网页内容的详细步骤解析与案例示例
Apache HttpClient是一个功能强大的开源HTTP客户端库,本文将详细介绍如何使用Apache HttpClient来爬取网页内容的步骤,并提供三个详细的案例示例,帮助读者更好地理解和应用。 一、导入Apache HttpClient库 在项目的pom.xml文件中添加依赖&a…...
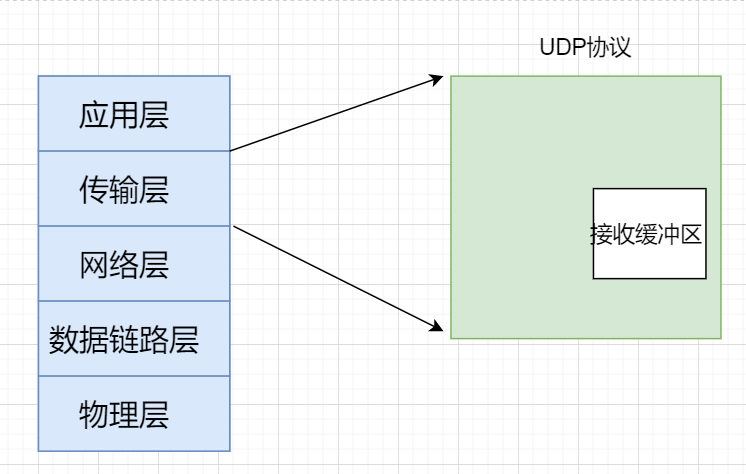
传输层协议—UDP协议
传输层协议—UDP协议 文章目录 传输层协议—UDP协议传输层再谈端口号端口号范围划分pidofnetstat UDP协议端格式UDP报文UDP特点UDP缓冲区基于UDP的应用层协议 传输层 在学习HTTP/HTTPS等应用层协议时,为了方便理解,可以简单认为HTTP将请求和响应直接发送…...

【改造中序遍历】 538. 把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树 解题思路 改造中序遍历算法因为中序遍历的结果都是有顺序的 升序排序,那么如果先遍历右子树 在遍历左子树 那么结果就是降序的最后我们设置一个变量 累加所有的中间值 那么得到的结果就是比当前节点大的所有节点的值 /*** Definiti…...

2022年11月工作经历
11月 招聘 最近招聘C程序员和黑盒测试员。由于第一次招聘不知道如何处理,不断和同事沟通,摸索出一套简单的规则。C程序员:力扣随机第二题,如果运气不好可以再随机一两次。黑盒测试员:力扣随机第二题或第三题ÿ…...

使用广播信道的数据链路层
使用广播信道的数据链路层 广播信道可以一对多通信。局域网使用的就是广播信道。局域网最主要的特点就是网络为一个单位所拥有,且地理范围和站点数目有限。局域网可按网络拓扑进行分为星形网、环形网、总线网。传统的以太网就是总线网,后来又演变为星…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
