leetcode-239-滑动窗口最大值
题意描述:
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
输入:nums = [1], k = 1
输出:[1]
解题思路:
Alice: 你咋想起来做这道了 ?
Bob: 我其实是在做另一道题目,多重背包的优化之单调队列优化,但是我不知道什么是单调队列,所以我需要先做一下这道题,学习一些单调队列。
Alice: 所有,有什么思路吗 ?
Bob: 学习的话,想个十分钟吧,然后看题解得了。

Alice: 好吧,题解看明白了吗 ?
Bob: 有点迷,我还是先上手写一下吧。
Alice: 没通过吧,有几个概念你要先了解。队列知道吧,先进先出。双端队列知道吗?两边都能进,两边都能出。你老用 JavaScript 的话,应该知道数组的 push pop shift unshift 这些方法吧,这就是双端队列。
Bob: 然后呢 ?
Alice:你还得知道单调队列,还有这题为啥需要单调队列来解。单调队列就是,队列中的值是单调的,单调就是数学上的那个单调,单调递增或者单调递减或者单调不增或者单调不减。
Bob: 那为啥要用单调队列呢 ?
Alice: 还是得读题啊。这题不是让求解滑动窗口的最大值吗 ?然后数组长度最大 10^5,k 的取值最大也是 10^5,按照最大的计算量 k取最大长度的一半也就是 5*10^4 然后每次都求最大值,计算量也就是 10^5 * (5 * 10^4)^2也就是 2.5 * 10^14, 时间限制是 1s 的话,一定会超时的。
Bob: 所以我们需要单调队列 ?
Alice: 差不多,单调队列非常适合这道题,这道题是让求 k 时间窗口的最大值,单调队列的头或尾一定是最大值。我们只需要在窗口滑动的过程中不断地维护队列就可以了。
Bob: 怎么维护呢 ?
Alice: 这里有两个点需要注意。1是要在维护队列的过程中不断干掉超出 k 时间窗口的值,2是要及时干掉那些不需要的值,比如说 nums[i] > nums[i-1] 的时候,nums[i-1] 就没必要继续留在队列中了,要求的是最大值 nums[i] 比 nums[i-1] 更大且更 ”年轻“ ,求最大值的时候 nums[i] 一定会覆盖 nums[i-1]。当然这里不止 i-1 前面 ”更老更小“ 的都应该干掉。
Bob: 所以我们的数据结构中还应该有下标,通过下标来计算某个值是否超出 k 时间窗口 ?
Alice: 对的,而另一个维护队列的时机就是在新元素入队之前,或者入队的时候。
Bob: 还有什么要注意的吗 ?
Alice: 有的,有两个点,一是初始化的时候也要维护单调队列,还有就是每次维护其实是在队首和队尾都要维护,队尾要干掉那些不必要的,队首要保证在 k 时间窗口内最大。
Bob: k 时间窗口最大我是这样理解的,队尾的维护会把比较小的干掉,这样队首元素出去之后,从队尾补上来的,应该总是剩下的最大的。
Alice: 对的。
Bob: 还是挺有技巧的,上代码吧。
代码:
/*** @param {number[]} nums* @param {number} k* @return {number[]}*/
var maxSlidingWindow = function(nums, k) {const ans = []// 初始化 queueconst queue = [];for(let i=0; i<k; ++i) {// 维护队尾,去除不必要的又老又小的值while (queue.length > 0 && queue[queue.length-1][0] <= nums[i]) {queue.pop();}// 新大值入队queue.push([nums[i], i]);}ans.push(queue[0][0]);for (let i=k; i<nums.length; ++i) {// 维护队尾,去除不必要的又老又小的值while (queue.length > 0 && queue[queue.length-1][0] <= nums[i]) {queue.pop();}// 新大值入队queue.push([nums[i], i]);// 维护队首while (queue.length > 0 && queue[0][1] + k <= i) {queue.shift();}ans.push(queue[0][0]);}return ans;
};
测试用例:
[9,10,9,-7,-4,-8,2,-6]
5
[10,10,9,2]
参考:
- 题目链接
- 相关题目-多重背包的单调队列优化
相关文章:

leetcode-239-滑动窗口最大值
题意描述: 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例: 输入:nums [1,3,-1,…...

基于大语言模型的智能问答系统应该包含哪些环节?
一个完整的基于 LLM 的端到端问答系统,应该包括用户输入检验、问题分流、模型响应、回答质量评估、Prompt 迭代、回归测试,随着规模增大,围绕 Prompt 的版本管理、自动化测试和安全防护也是重要的话题,本篇文章就来探索下这个过程…...

【Cesium创造属于你的地球】相机系统
相机系统里面有setView,flyTo,lookAt,viewBoundingsphere这几种方法,以下是相关的使用方法,学起来!!! setView 该方法可以直接切换相机视口,从而不需要通过一个飞入的效…...

运维困局下确保系统稳定的可行性
业务高速发展背后的困局 随着业务的快速发展,运维体系也逐步的完善起来。业务的稳定性和服务质量也在监控、可用性等体系的相互环抱下健康地成长。所有的问题、故障及影响稳定性的因素都在可控、可收敛的范围内,一切都向着好的方向发展。 这一切的背后…...
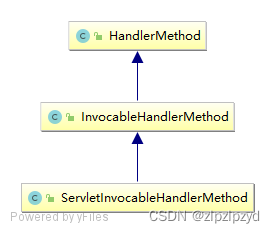
springmvc中DispatcherServlet关键对象
以下代码为 spring boot 2.7.15 中自带的 spring 5.3.29 RequestMappingInfo 请求方法相关信息封装,对应的信息解析在 RequestMappingHandlerMapping 的 createRequestMappingInfo() 中实现。 对于 RequestMapping 赋值的相关信息进行解析 protected RequestMappi…...

某微e-office协同管理系统存在任意文件读取漏洞复现 CNVD-2022-07603
目录 1.漏洞概述 2.影响版本 3.漏洞等级 4.漏洞复现 5.Nuclei自动化扫描POC 某微e-office协同管理系统存在任意文件读取漏洞分析 CNVD-2022-07603https://blog.csdn.net/qq_41490561/article/details/133469649...
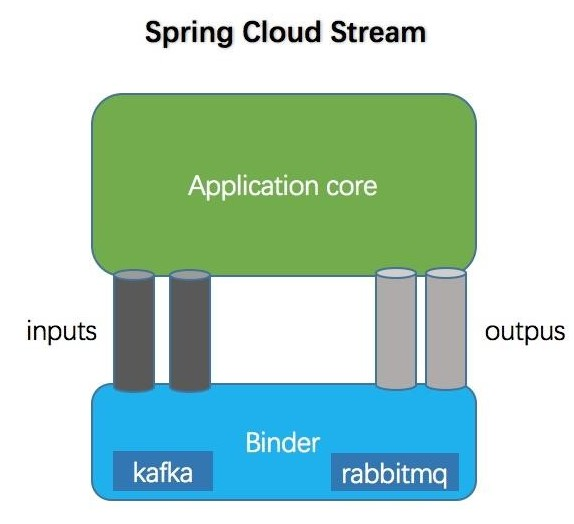
消息驱动 —— SpringCloud Stream
Stream 简介 Spring Cloud Stream 是用于构建消息驱动的微服务应用程序的框架,提供了多种中间件的合理配置 Spring Cloud Stream 包含以下核心概念: Destination Binders:目标绑定器,目标指的是 Kafka 或者 RabbitMQ࿰…...

使用Apache HttpClient爬取网页内容的详细步骤解析与案例示例
Apache HttpClient是一个功能强大的开源HTTP客户端库,本文将详细介绍如何使用Apache HttpClient来爬取网页内容的步骤,并提供三个详细的案例示例,帮助读者更好地理解和应用。 一、导入Apache HttpClient库 在项目的pom.xml文件中添加依赖&a…...
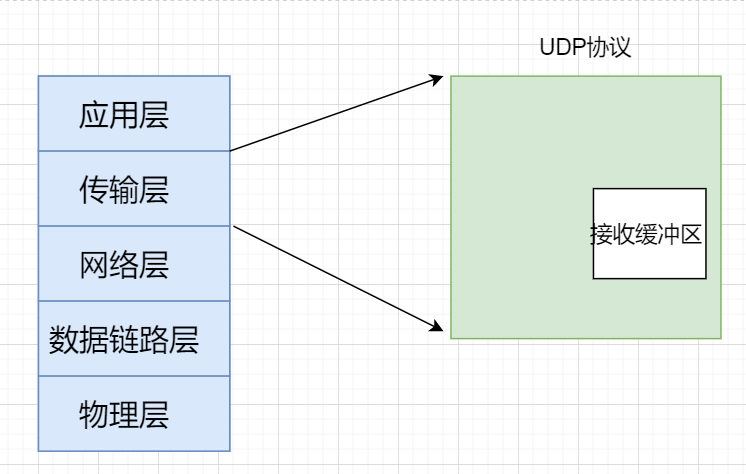
传输层协议—UDP协议
传输层协议—UDP协议 文章目录 传输层协议—UDP协议传输层再谈端口号端口号范围划分pidofnetstat UDP协议端格式UDP报文UDP特点UDP缓冲区基于UDP的应用层协议 传输层 在学习HTTP/HTTPS等应用层协议时,为了方便理解,可以简单认为HTTP将请求和响应直接发送…...

【改造中序遍历】 538. 把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树 解题思路 改造中序遍历算法因为中序遍历的结果都是有顺序的 升序排序,那么如果先遍历右子树 在遍历左子树 那么结果就是降序的最后我们设置一个变量 累加所有的中间值 那么得到的结果就是比当前节点大的所有节点的值 /*** Definiti…...

2022年11月工作经历
11月 招聘 最近招聘C程序员和黑盒测试员。由于第一次招聘不知道如何处理,不断和同事沟通,摸索出一套简单的规则。C程序员:力扣随机第二题,如果运气不好可以再随机一两次。黑盒测试员:力扣随机第二题或第三题ÿ…...

使用广播信道的数据链路层
使用广播信道的数据链路层 广播信道可以一对多通信。局域网使用的就是广播信道。局域网最主要的特点就是网络为一个单位所拥有,且地理范围和站点数目有限。局域网可按网络拓扑进行分为星形网、环形网、总线网。传统的以太网就是总线网,后来又演变为星…...

第3章-指标体系与数据可视化-3.1.2-Seaborn绘图库
目录 3.1.2 Seaborn绘图库 1. 带核密度估计的直方图 2. 二元分布图 一维正态分布 联合分布...

excel中将一个sheet表根据条件分成多个sheet表
有如下excel表,要求:按月份将每月的情况放在一个sheet中。 目测有6个月,就应该有6个sheet,每个sheet中体现本月的情况。 一、首先增加一个辅助列,月份,使用month函数即可。 填充此列所有。然后复制【月份】…...

案例突破——再探策略模式
再探设计模式 一、背景介绍二、 思路方案三、过程1. 策略模式基本概念2. 策略模式类图3. 策略模式基本代码策略类抽象策略类Context类客户端 4. 策略模式还可以进行优化的地方5. 对策略模式的优化(配置文件反射) 四、总结五、升华 一、背景介绍 在做项目…...
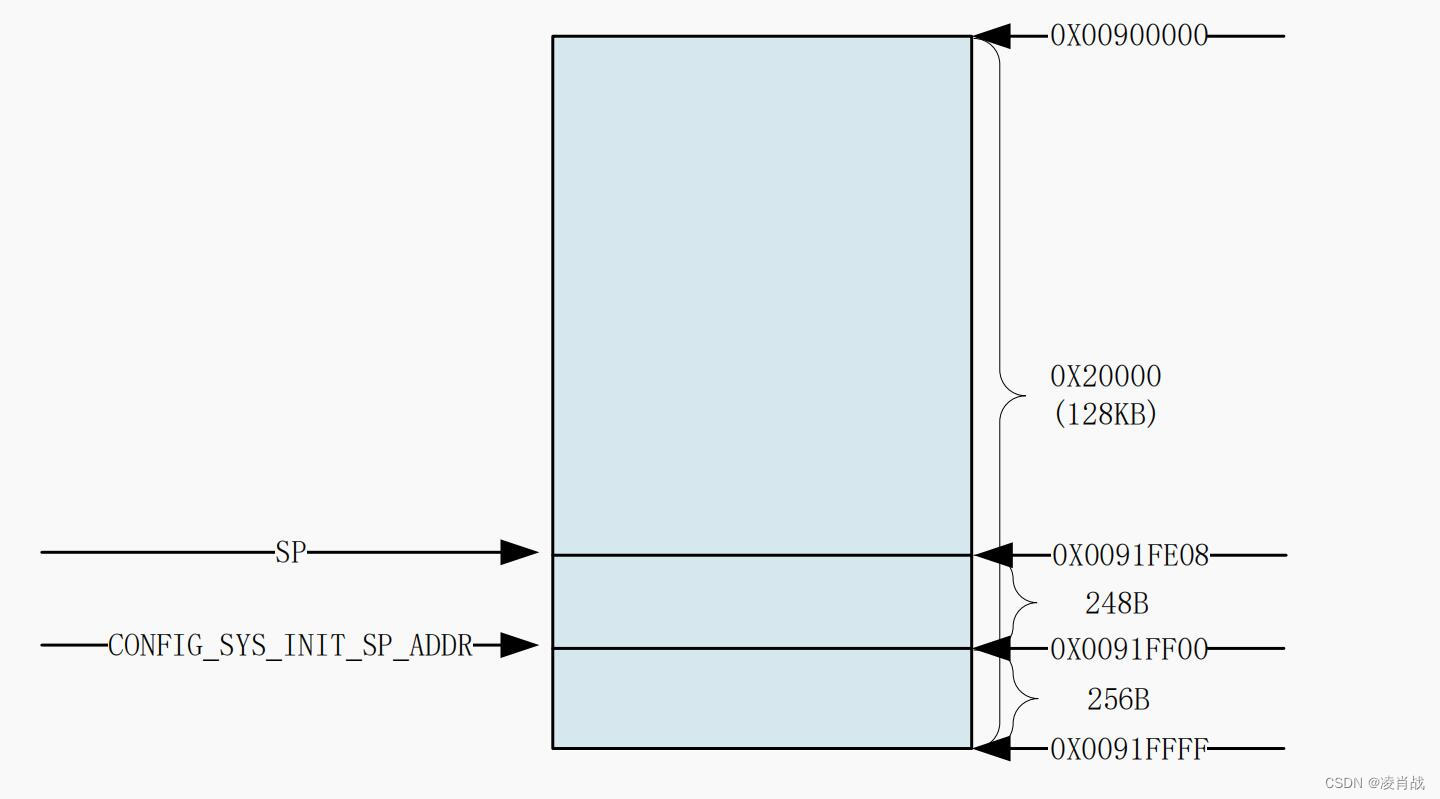
uboot启动流程-涉及lowlevel_init汇编函数
一. uboot启动流程涉及函数 之前文章简单分析了 uboot启动流程的开始,从链接脚本文件 u-boot.lds 中,我们已经知道了入口点是 arch/arm/lib/vectors.S 文件中的 _start函数。 _start函数:调用了 reset 函数,reset 函数内部&…...
质数距离 - 如何在较合理的时间复杂度内求2e9范围内的质数
求l、r之间的质数,范围在2e9,但l、r的差值不大,在1e6范围内 先求出 内的质数,然后拿这个指数去筛[l, r]范围内的即可 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \…...

八、3d场景的区域光墙
在遇到区域展示的时候我们就能看到炫酷的区域选中效果,那么代码是怎么编辑的呢,今天咱们就好好说说,下面看实现效果。 思路: 首先,光墙肯定有多个,那么必须要创建一个新的js文件来作为他的原型对象。这个光…...
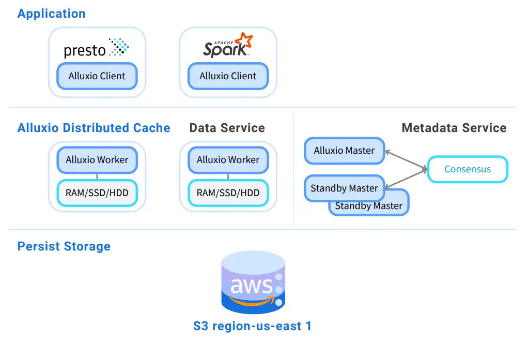
深入探讨 Presto 中的缓存
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 Presto是一种流行的开源分布式SQL引擎,使组织能够在多个数据源上大规模运行交互式分析查询。缓存是一种典型的提高 Presto 查询性能的优化技术。它为 Prest…...
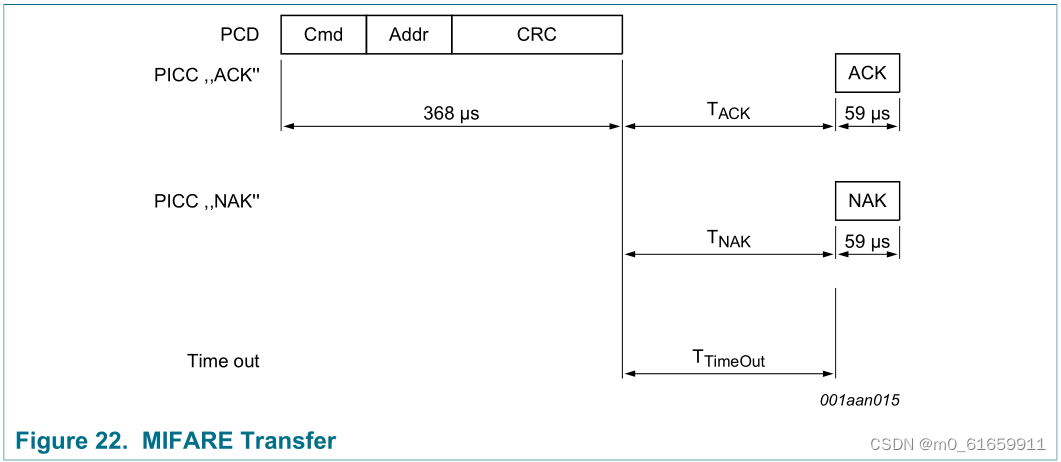
3.物联网射频识别,(高频)RFID应用ISO14443-2协议,(校园卡)Mifare S50卡
一。ISO14443-2协议简介 1.ISO14443协议组成及部分缩略语 (1)14443协议组成(下面的协议简介会详细介绍) 14443-1 物理特性 14443-2 射频功率和信号接口 14443-3 初始化和防冲突 (分为Type A、Type B两种接口&…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
