算法通过村第十一关-位运算|白银笔记|高频题目
文章目录
- 前言
- 1. 位移的妙用
- 1.1 位1的个数
- 1.2 比特位计算
- 1.3 颠倒无符号整数
- 2. 位实现加减乘除专题
- 2.1 位运算实现加法
- 2.2 递归乘法
- 总结
前言
提示:他不是不想多明白些,但是每每在该用脑子的时候,他用了感情。 --老舍《黑白李》
与位运算和数学有关的题目真的不少,很多都是有一定技巧的,好在这些技巧都是相对固定的,我们要做好积累。
1. 位移的妙用
位移操作是一个很重要的问题,可以统计数字中1的个数,在很多高性能的软件中也是大量运用,我们先来看看下面这几道高频题目。
1.1 位1的个数
参考题目介绍:191. 位1的个数 - 力扣(LeetCode)


拓展一下:16进制时怎么统计0的个数
首先我们可以根据题目的要求直接计算,题目给定的n是32位二进制表示下的一个整数,计算位1的个数最简单的方式就是遍历一边n的二进制表示的每一位,判断每一位是否为1,同时还要进行统计。
那问题就是变成了,如何通过位运算来识别到1:举个栗子🌰
[0000 1001 0010 0001 0001 0001 1100 1101]
首先我们需要注意到识别最低为的1,可以这么做
[0000 1001 0010 0001 0001 0001 1100 1101]
& [0000 0000 0000 0000 0000 0000 0000 0001]
= [0000 0000 0000 0000 0000 0000 0000 0001]
也就是说将原始数字和1进行&运算就能够知道最低位是不是1了,那么其他位置怎么处理呢?
这里有两种思路
- 让1不断地左移
- 将原始数据不断的右移
例如将原始数据右移就是
[0000 0100 1001 0000 1000 1000 1110 0110]
& [0000 0000 0000 0000 0000 0000 0000 0001]
= [0000 0000 0000 0000 0000 0000 0000 0000]
很明显的就可以判断出第二位是0,然后继续将原始数据右移可以依次判断出每个位置是不是1了。所以这里可以总结下(n >> i) & 1就可以了,所以代码写起来也简单了:
/*** 方法1:n整体循环移位** @param n* @return*/public static int hammingWeight1(int n) {int count = 0;for(int i = 0; i < 32; i++){count += (n >> i) & 1;}return count;}
这个题目也可以通过左移1来实现的,该问题可以留作作业。你可以试着改下代码。
上面的代码写出来,这个问题问题就基本上及格了,但是不是最经典的解法,我们进一步分析,按位与运算的一个性质,对于整数n,计算n&(n - 1)的结果是将n的二进制表示最后一个1变成0。利用这个性质。令n = n &(n - 1),则n的二进制数中的1的个数减少一个,重复该操作,知道n的二进制位中的全部位数变成0,则该操作的次数即时n的位上1的个数。什么意思呢?我们看下图解:
n [0000 0100 1001 0000 1000 1000 1110 0110]
n-1 [0000 0100 1001 0000 1000 1000 1110 0101]
n& (n - 1) = [0000 0100 1001 0000 1000 1000 1110 0100]
可以看到此时n&(n - 1)的结果是比n少了一个1,此时我们令n = n &(n - 1),继续执行上述操作
n [0000 0100 1001 0000 1000 1000 1110 0100]
n-1 [0000 0100 1001 0000 1000 1000 1110 0011]
n& (n - 1) = [0000 0100 1001 0000 1000 1000 1110 0000]
可以看到此时n&(n - 1)的结果是比n少了一个1,此时我们令n = n &(n - 1),继续执行上述操作,循环下去,就可以统计到1的位数。
那么什么时候停下来?很显然当n都变成0时,否则就说明数据中是由1,就可以继续循环了。所以停止条件时n == 0,n 的二进制表示的全部位数都是0,代码也很好写的🤔。
/*** 方法2:根据1的数量循环** @param n* @return*/public static int hammingWeight2(int n) {int count = 0;while(n != 0){n = n & (n - 1);count ++;}return count;}
上面的两种解法,第一种循环的次数取决于原始数字的位数,而第二种的取决于1的个数,效率明显要快得多,使用n = n & (n - 1)计算是位运算的一个经典技巧,该结论也完美使用与下面的题目:
1.2 比特位计算
参考题目介绍:338. 比特位计数 - 力扣(LeetCode)

最直观的方法就是从0到num的每个数直接计算一下“1的个数”。每个int的数都可以用32的二进制位数表示,只要遍历其二进制表示的每一位即可得到1的数目:
/*** 方法1:统一移位统计** @param num* @return*/public static int[] countBits(int num) {int[] bits = new int[num + 1];for(int i = 0; i <= num; i++){for(int j = 0; j < 32; j++){bits[i] += (i >> j) & 1;}}return bits;}结合上面学来的技巧,可以快速提升速度。与位运算(&)的性质:对于任意整数x,令 x = x & (x - 1),该运算将x的二进制表示的最后一个1 变成0.因此,对于x重复该操作,直到将x变为0,则操作次数就是x的【移位比特数】
/*** 方法2:通过技巧x &= (x - 1);计算** @param num* @return*/public static int[] countBits2(int num) {int[] bits = new int[num+1];for(int i=0; i<=num; i++){bits[i] = countOnes(i);}return bits;}private static int countOnes(int num) {int count = 0;while(num != 0){num = num &(num - 1);count++;}return count;}
有没有发现比特位计算和1的个数计算规则是一样的?这就是为什么我么你说了解一道题,就可以解决很多题目。
1.3 颠倒无符号整数
参考题目介绍:190. 颠倒二进制位 - 力扣(LeetCode)


首先这里说的是无符号位,也就是说不用考虑正负的问题,最高位的1也不代表符号位,这就省了一些麻烦。
我们注意到对于n的二进制表示的从低位到高位第i位,在颠倒之后变成第31 - i 位( 0 <= i < 32),所以可以从低位到高位遍历n的二进制表示的每一位,将其放在颠倒之后的位置,最后相加就可以了。
看一个栗子🌰,方便演示,我们去较短的16位:
原始数据: [1001 1111 0000 0110](低位)第一步:获取n的最低为0,然后将其右移16-1位15位,得到:reversed: [0*** **** **** ****]n右移移位: [0100 1111 1000 0011]第二步:继续获取n的最低为0,然后将其右移15-1位14位,并于reversed相加得到:reversed: [01** **** **** ****]n右移移位: [0010 0111 1100 0001]......继续直到n全部变成0:理解之后,实现起来就比较容以了。由于Java不存在无符号类型,所有的便是整数的类型都是有符号类型的,因此需要区分算术右移和逻辑右移,在Java中,算术右移的符号是>>,逻辑右移的符号是>>>。
/*** 通过移位实现反转** @param n* @return*/public static int reverseBits(int n) {int reversed = 0, power = 31;while(n != 0){reversed += (n & 1) << power;n >>>= 1;power--;}return reversed;}
本题还有其他解法,有一种分块的思想,n的二进制表示有32位,可以将n的二进制表示成较小的块,然后将每个块的二进制分别颠倒,最后将每个块的结果合并得到最中的结果。当然这个也是分治的策略。将n的32位二进制便是分成两个16位的块,并将这两个块颠倒;然后对每个16位的块重复上述操作,直到达到位1位的块,我们这里演示一下:
具体的做法如下:
下面的代码中,每一行分别将n分成16位,8位,4位,2位,1位的块,即把每个块分成较小的块,并将分成的两个较小的块颠倒。同时需要注意,使用Java实现是,右移运算必须使用逻辑右移。由于固定的32位,我们可以不必写循环或者递归,可以直接写。
/*** 通过分块实现反转** @param n* @return*/public static int reverseBits2(int n) {n = (n >>> 16) | (n << 16);n = ((n & 0xFF00FF00) >>> 8) | ((n & 0x00FF00FF) << 8);n = ((n & 0xF0F0F0F0) >>> 4) | ((n & 0x0F0F0F0F) << 4);n = ((n & 0xCCCCCCCC) >>> 2) | ((n & 0x33333333) << 2);n = ((n & 0xAAAAAAAA) >>> 1) | ((n & 0x55555555) << 1);return n;}
这种方法在JDK、Dubbo等源码中都可以见到,特别是涉及协议解析的场景几乎都不少这样的操作。积累相关的技巧,可以方便面试,也有助于阅读源码。(面试算法和工程算法)。
2. 位实现加减乘除专题
在计算机中,位运算的效率比加减乘除的效率要高,因此在高性能软件的源码中大量应用,而且计算机里的各种操作本质上也是位运算。这里就研究下相关问题。
2.1 位运算实现加法
参考题目介绍:371. 两整数之和 - 力扣(LeetCode)

既然不能使用+和-,那么只能使用位运算了。我们看一下位运算的相加的情况:
[1] 0 + 0 = 0
[2] 0 + 1 = 1
[3] 1 + 0 = 1
[4] 1 + 1 = 0 (发生了位移,这里应该是10 相当于进位)
两个位相加的时候,我们无非要考虑两个问题:进位部分是是么,不知道进位部分是什么。从上面的结果可以看到,对于a和b两个数不进位部分的情况是:相同为0,不同为1,这个不就是a^b吗?
而对于进位,我们发现只有a和b都是1的时候才回进位,而且进位只有1,这不就是a&b = 1吗?然后位数由1位变成了两位,也就是上面的[4]的样子,那么将1向前挪一下呢?手动位移一下就好了,也就是(a&b) << 1。所以我们得出两条结论:
- 不进位的部分:用a^b计算就可以了。
- 是否进位:已经进位值使用(a & b) << 1计算就可以了。
于是,我们可以将整数a和b的和,拆分位a和b的无进位加法结果与进位结果的和。
代码也是很简单:
public int getSum(int a, int b) {while(b != 0){int sign = (a & b) << 1;a = a ^ b;b = sign;}return a;}
2.2 递归乘法
参考题目地址:面试题 08.05. 递归乘法 - 力扣(LeetCode)

如果不让用*来计算,一种是将一个作为循环的参数,对另一个进行累加,但是这样的效果太低了,所以要考虑位运算。
首先,求得A和B得最小值和最大值,其中得最小值当做乘数(为什么要选最小值呢,因为选择最小值乘的次数少,可以说算的少),将其拆成分成2得幂得和,即min = a_0 * 2^0+a_1*2_1+…+a_i *2 ^ i + …其中a_i取0或者1。其实就是用二进制得视角取看待min,比如12得二进制表示可以是[0000 1100]也就说是1000 + 0100。就比如这样:
13*12 = 13 * (8 + 4) = 13 * 8 + 13 * 4 = (13 << 3) + (13 << 2);
上面仍需要左移5次,存在重复计算,可以进一步简化:
假设我们需要的结果是ans:
定义临时变量:temp = 13 << 2 = 52 计算之后,可以先让ans = 52;
然后temp继续左移一次 temp = 52 << 1 = 104,此时再让ans = ans + temp
这样只需要执行三次位移和一次加法,实现代码:
public int multiply(int A, int B) {int min = Math.min(A,B);int max = Math.max(A,B);int ans = 0;for(int i = 0; min != 0;i++){// 只有当位1 的时候才使用加if((min & 1) == 1){ans += max;}min >>= 1;max += max;}return ans;}
拓展:
你可以尝试尝试除法,推荐题目:29. 两数相除 - 力扣(LeetCode)
总结
提示:位运算技巧;位运算高频题目;相加和相乘;翻转和递归:
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题

相关文章:

算法通过村第十一关-位运算|白银笔记|高频题目
文章目录 前言1. 位移的妙用1.1 位1的个数1.2 比特位计算1.3 颠倒无符号整数 2. 位实现加减乘除专题2.1 位运算实现加法2.2 递归乘法 总结 前言 提示:他不是不想多明白些,但是每每在该用脑子的时候,他用了感情。 --老舍《黑白李》 与位运算和…...
04、EL和JSTL核心技术
目录 1 EL表达式(熟悉) 1.1 基本概念 1.2 主要功能 1.3 访问内置对象的数据 1.3.1访问方式 1.3.2 执行流程 1.4 访问请求参数的数据 1.5 访问Bean对象的属性 1.5.1 访问方式 1.5.2 主要区别 1.6 访问集合中的数据 1.7 常用的内置对象 …...
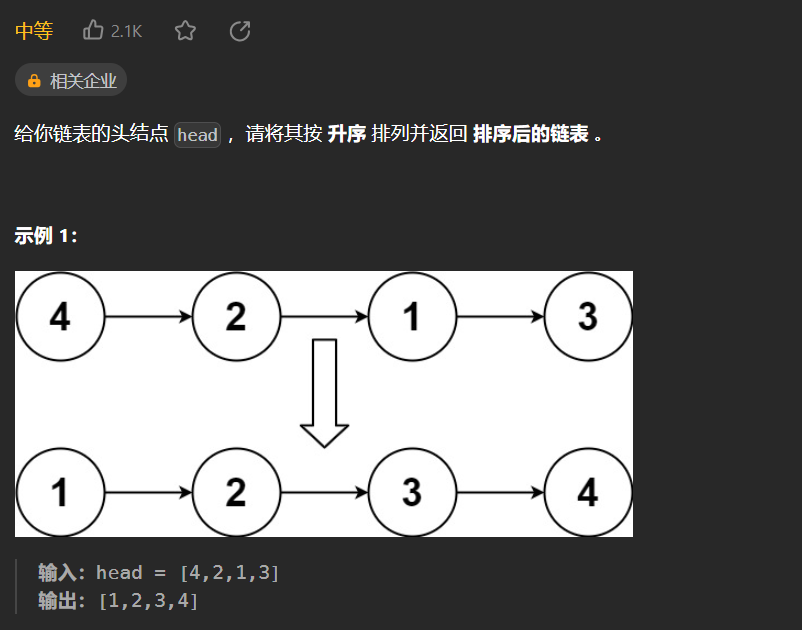
【LeetCode热题100】--148.排序链表
148.排序链表 对链表进行排序最适合的算法就是归并排序: 对链表自顶向下归并排序的过程: 找到链表的中点,以中点为分界,将链表拆分成两个子链表,寻找链表的中点可以使用快慢指针的做法,快指针每次移动 2步…...

分布式并行训练(DP、DDP、DeepSpeed)
[pytorch distributed] 01 nn.DataParallel 数据并行初步 数据并行 vs. 模型并行 数据并行:模型拷贝(per device),数据 split/chunk(对batch切分) 每个device上都拷贝一份完整模型,每个device分…...

Linux- fg命令 bg命令
fg fg是Unix-like操作系统(如Linux和macOS)中的一个shell内建命令,用于将后台作业带到前台执行。这个命令常用于与bg(后台执行)命令和jobs(列出当前作业)命令一起,进行shell中的作业…...

leetcode第362场周赛
2873. 有序三元组中的最大值 I 核心思想:由于这题数据范围比较小,直接枚举i,j,k即可。 2874. 有序三元组中的最大值 II 核心思想:这题是在2873题目的基础上将数据范围进行了增加,意味着我们需要对上面的代码进行优化。两种优化方…...
图神经网络GNN(一)GraphEmbedding
DeepWalk 使用随机游走采样得到每个结点x的上下文信息,记作Context(x)。 SkipGram优化的目标函数:P(Context(x)|x;θ) θ argmax P(Context(x)|x;θ) DeepWalk这种GraphEmbedding方法是一种无监督方法,个人理解有点类似生成模型的Encoder过程…...
多目标平衡优化器黏菌算法(MOEOSMA)求解CEC2020多模式多目标优化
多目标平衡优化器黏菌算法(MOEOSMA)比现有的多目标黏菌算法具有更好的优化性能。在MOEOSMA中,动态系数用于调整勘探和开采趋势。采用精英存档机制来促进算法的收敛性。使用拥挤距离法来保持Pareto前沿的分布。采用平衡池策略模拟黏菌的协同觅…...
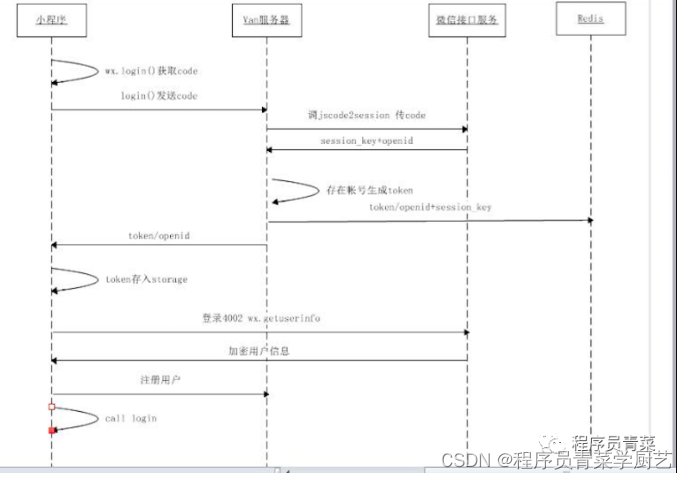
快速开发微信小程序之一登录认证
一、背景 记得11、12年的时候大家一窝蜂的开始做客户端Android、IOS开发,我是14年才开始做Andoird开发,干了两年多,然后18年左右微信小程序火了,我也做了两个小程序,一个是将原有牛奶公众号的功能迁移到小程序&#x…...
和Mapper映射文件(XXXMapper.xml)模板)
Mybatis配置文件(mybatis-config.xml)和Mapper映射文件(XXXMapper.xml)模板
配置文件 ${dirver} ---> com.mysql.jdbc.Driver ${url} ---> jdbc:mysql://localhost:3306/数据库名 <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE configurationPUBLIC "-//mybatis.org//DTD Config 3.0//EN""h…...
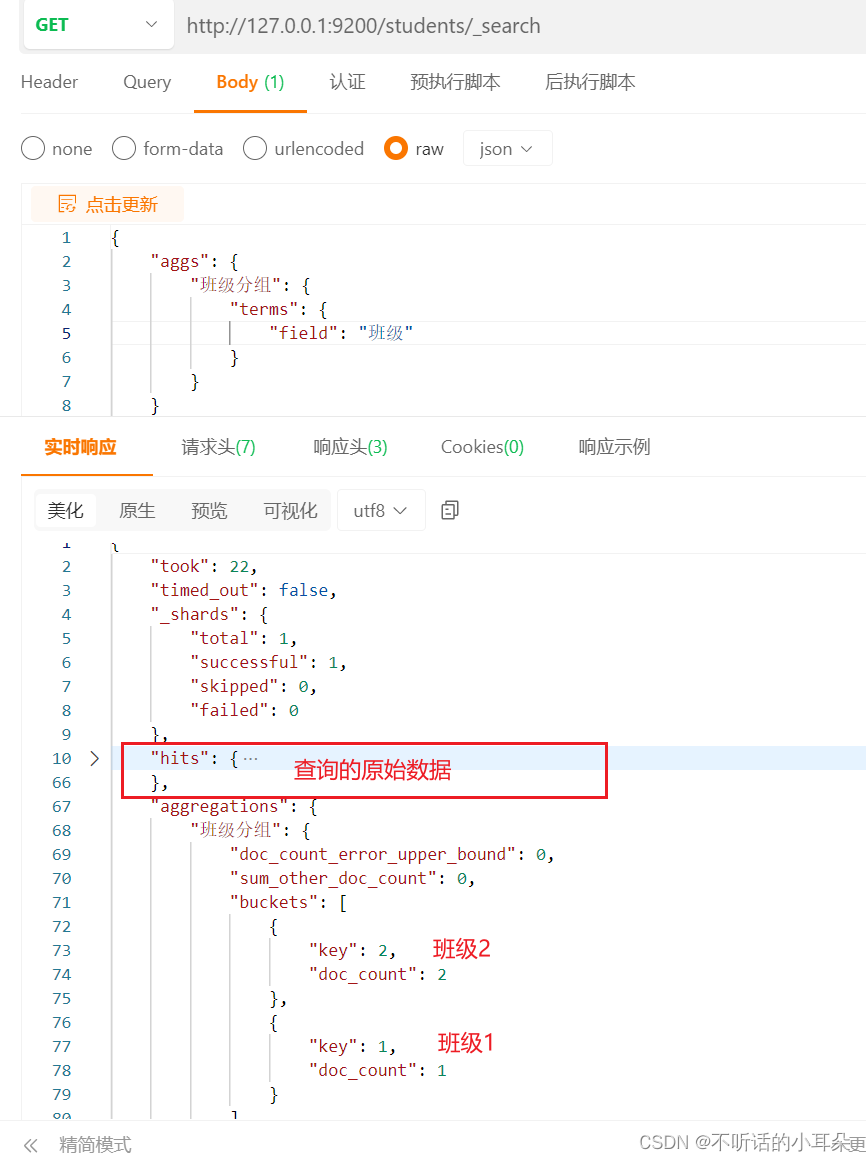
4. 条件查询
首先区分下match,match_phrase,term, 参考:https://zhuanlan.zhihu.com/p/592767668?utm_id0 1、全量查询分页指定source 示例:请求地址为http://127.0.0.1:9200/students/_search,请求体为: {"query":…...

【VIM】初步认识VIM-2
2-6 Vim 如何搜索替换_哔哩哔哩_bilibili 1-6行将self改成this 精确替换quack单词为交...
《HelloGitHub》第 90 期
兴趣是最好的老师,HelloGitHub 让你对编程感兴趣! 简介 HelloGitHub 分享 GitHub 上有趣、入门级的开源项目。 https://github.com/521xueweihan/HelloGitHub 这里有实战项目、入门教程、黑科技、开源书籍、大厂开源项目等,涵盖多种编程语言 …...
(与flink的结合)--Flink 中hudi clean操作)
Apache Hudi初探(五)(与flink的结合)--Flink 中hudi clean操作
背景 本文主要是具体说说Flink中的clean操作的实现 杂说闲谈 在flink中主要是CleanFunction函数: Overridepublic void open(Configuration parameters) throws Exception {super.open(parameters);this.writeClient FlinkWriteClients.createWriteClient(conf,…...

stream对list数据进行多字段去重
方法一: //根据sj和name去重 List<NursingHandover> testList list.stream().collect(Collectors.collectingAndThen(Collectors.toCollection(() -> new TreeSet<>(Comparator.comparing(o -> o.getj() ";" o.getName() ";&…...
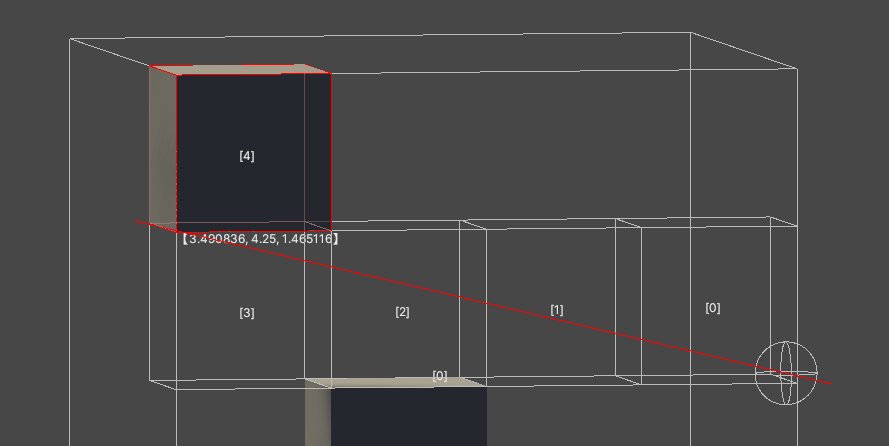
一种基于体素的射线检测
效果 基于体素的射线检测 一个漏检的射线检测 从起点一直递增指定步长即可得到一个稀疏的检测 bool Raycast(Vector3 from, Vector3 forword, float maxDistance){int loop 6666;Vector3 pos from;Debug.DrawLine(from, from forword * maxDistance, Color.red);while (loo…...

利用Docker安装Protostar
文章目录 一、Protostar介绍二、Ubuntu下安装docker三、安装Protostar 一、Protostar介绍 Protostar是一个免费的Linux镜像演练环境,包含五个系列共23道漏洞分析和利用实战题目。 Protostar的安装有两种方式 第一种是下载镜像并安装虚拟机https://github.com/Exp…...

go基础语法10问
1.使用值为 nil 的 slice、map会发生啥 允许对值为 nil 的 slice 添加元素,但对值为 nil 的 map 添加元素,则会造成运行时 panic。 // map 错误示例 func main() {var m map[string]intm["one"] 1 // error: panic: assignment to entry i…...

SpringCloud + SpringGateway 解决Get请求传参为特殊字符导致400无法通过网关转发的问题
title: “SpringCloud SpringGateway 解决Get请求传参为特殊字符导致400无法通过网关转发的问题” createTime: 2021-11-24T10:27:5708:00 updateTime: 2021-11-24T10:27:5708:00 draft: false author: “Atomicyo” tags: [“tomcat”] categories: [“java”] description: …...

vim基本操作
功能: 命令行模式下的文本编辑器。根据文件扩展名自动判别编程语言。支持代码缩进、代码高亮等功能。使用方式:vim filename 如果已有该文件,则打开它。 如果没有该文件,则打开个一个新的文件,并命名为filename 模式…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
