傅里叶系列 P1 的定价选项
- 如果您想了解更多信息,请查看第 2 部分和第 3 部分。

一、说明
这是第一篇文章,我将帮助您获得如何使用这个新的强大工具来解决金融中的半分析问题并取代您的蒙特卡洛方法的直觉。
我们都知道并喜欢蒙特卡洛数字积分方法,但是如果我告诉你你可以用虚数和傅里叶级数来代替蒙特卡洛呢?
主要好处是速度,这在期权定价中非常重要。这非常重要,因为用于定价股票期权的赫斯顿模型需要数字积分,蒙特卡罗大约需要 100 毫秒,傅里叶级数需要几毫秒。
二、第 1 部分:但是什么是傅里叶级数?
对于任何函数 f 和区间 a,b,我们可以将 f(x) 近似为余弦和正弦的无限和,L = b-a。
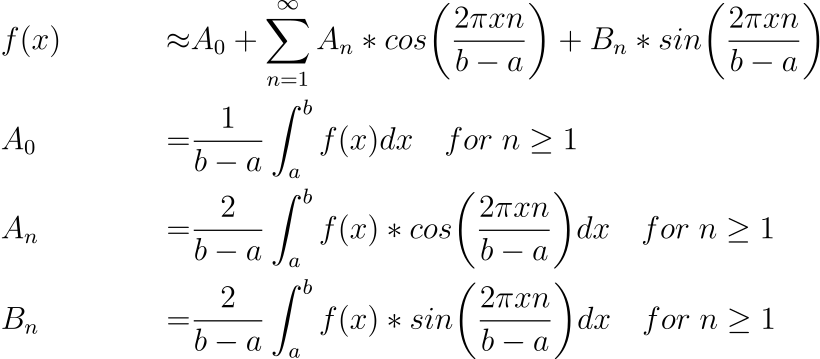
三、第 2 部分:将数学公式应用于 Python
def get_fourier_approx(f, x:np.array, a:float, b:float, N:int):fa = lambda x, n : f(x) * cos((2*pi*n*x)/(b - a))fb = lambda x, n : f(x) * sin((2*pi*n*x)/(b - a))A0 = 1/(b - a) * quad(f, a, b, limit=200)[0]Cosine_Sine_Sum = np.zeros_like(x)for n in range(1, N+1):A = 2/(b - a) * quad(fa, a, b, args=(n), limit=200)[0]B = 2/(b - a) * quad(fb, a, b, args=(n), limit=200)[0]Cosine_Sine_Sum += A*cos((2*pi*n*x)/(b - a)) + B*sin((2*pi*n*x)/(b - a))fx = A0 + Cosine_Sine_Sumreturn fxa = -6
b = 6
x = np.linspace(a, b, 1_000)
y = f(x)fig, (ax1, ax2) = plt.subplots(2, figsize=(20,12))
blue_shades = ['#0000FF', '#3399FF', '#66B2FF', '#99CCFF', '#CCE5FF']avg_residuals = []
Ns = [8, 16, 32, 64, 128]
for i, N in enumerate(Ns):fx = get_fourier_approx(f=f, x=x, a=a, b=b, N=N)ax1.plot(x,fx, blue_shades[i], label=f'N = {N}')ax2.plot(x,y-fx, blue_shades[i], label=f'N = {N}')avg_residuals.append(np.abs(y-fx).mean())ax1.set_title('Fourier Transform of f(x)')
ax1.plot(x,y,'tab:red', linestyle='--')
ax2.set_title('Residuals')
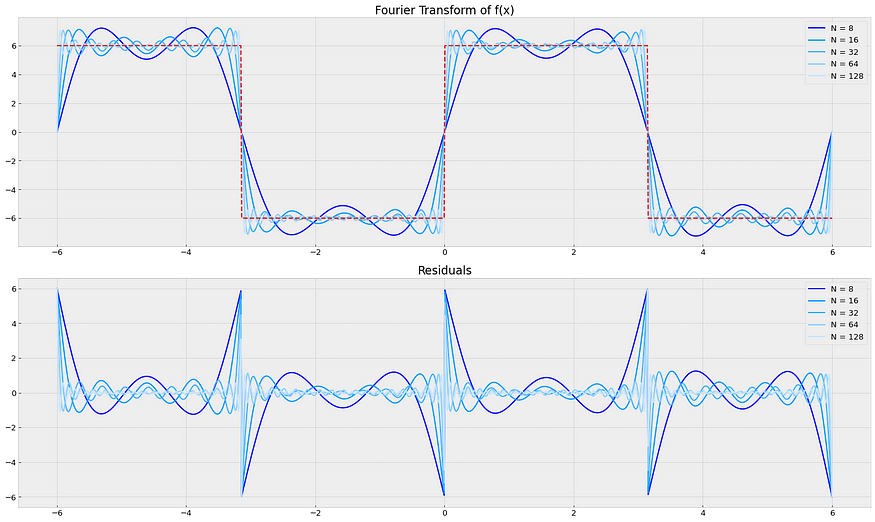
plt.tight_layout() ; ax1.legend();ax2.legend() ; plt.show()pd.Series(avg_residuals, index=Ns, name='Avg Residual')3.1 方形功能:
来源:笔记本
N Avg. Residual
--------------------
8 1.311711
16 0.784683
32 0.440387
64 0.268449
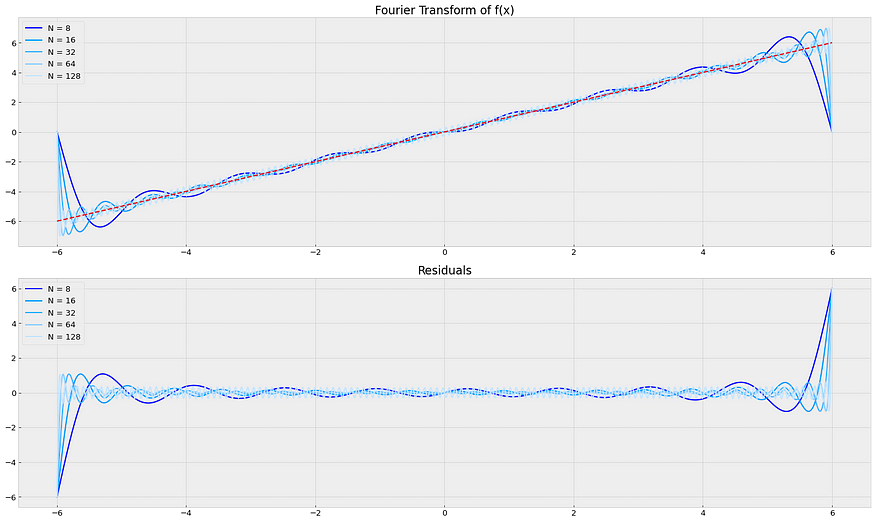
128 0.1546043.2 线路功能:
来源:笔记本
N Avg. Residual
--------------------
8 0.447389
16 0.264635
32 0.153540
64 0.088745
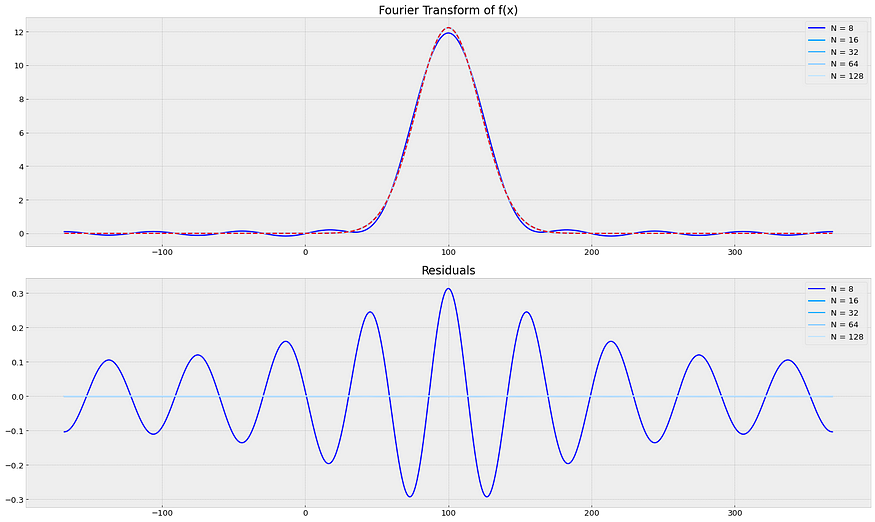
128 0.0521473.3 正态分布
- 在 [0, 12] 中缩放 y,其中:
- 平均值 = 100- 标准 = 0.1 *sqrt(5)*100- a = 100 -12 * 标准
- b = 100
+12 * 标准
来源:笔记本
N Avg. Residual
--------------------
8 1.092374e-01
16 8.326020e-05
32 6.878539e-14
64 5.721031e-14
128 5.170898e-143.3 议论
- 所有分布都按比例缩放,使 y 范围从 [0,12] 开始,因此我们可以比较残差的大小。
- 从绘图和残差可以看出,函数的曲线越大,傅里叶级数收敛到正确值的速度就越快。我们将此属性用作正态,并且对数正态不需要很多项来计算,在我们的近似中具有足够的准确性。
- 数据开头和结尾的误差明显更高。因此,最好包含比预期使用的限制更高的限制。例如,当您需要 ±4 时计算 ±3std。这使得深度价外期权更难计算。
四、第3部分 S(T)的对数正态分布
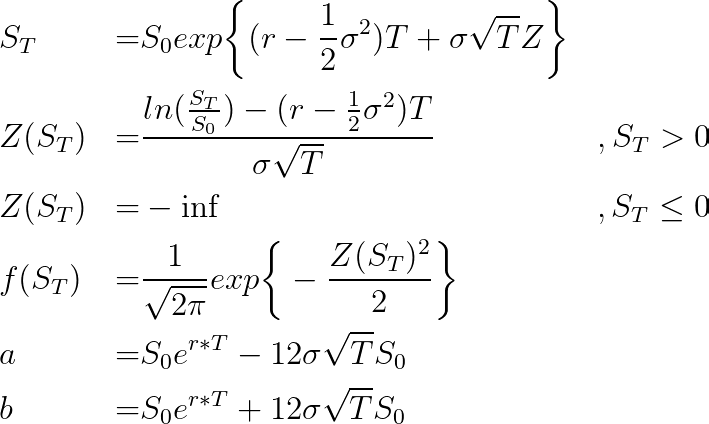
S_T遵循 Q 下的简单 GBM,我们可以使用以下等式推导出S_T的概率密度:
现在我们可以使用以下函数在 Python 中定义 f(S_T),并将下限定义为 ( 0, S_0*exp(r*T) + 12 * sigma*sqrt(T)*S_0 )
S0 = 100
r = 0.05
sigma = 0.1
T = 5.0Z = lambda St : np.where(St > 0, ((log(St/S0) - (r - .5*sigma)*T)/(sqrt(T)*sigma)), -np.inf)
f = lambda x : norm.pdf(Z(x))a = S0*exp(r*T) - 12 * sigma*sqrt(T)*S0
b = S0*exp(r*T) + 12 * sigma*sqrt(T)*S0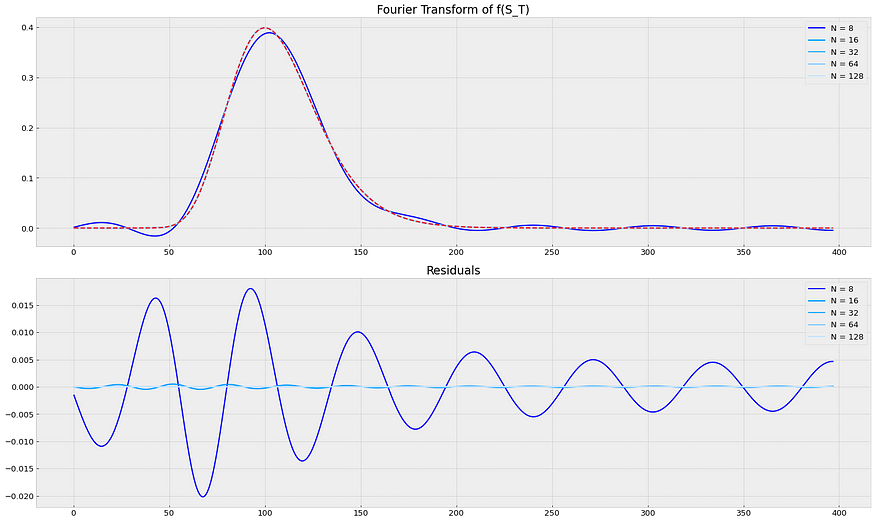
Source: Notebook
N Avg. (scaled) Residual Avg. Residual Execution Time (sec)
----------------------------------------------------------------------------
8 0.176429 5.880975e-03 0.112720
16 0.004235 1.411566e-04 0.246473
32 0.000030 9.855127e-07 0.624209
64 0.000027 8.918504e-07 1.936948
128 0.000026 8.530034e-07 6.7410194.1 言论:
- 我包括了缩放和非缩放残差。缩放残差对应于(不正确的)缩放概率,使得 max{y}=12,其中(正确的)非缩放,max{y}=0.4。这样做是为了将对数正态分布的拟合与上面绘制的其他函数进行比较。
- 我们可以推断出,由于形状不对称,对数正态分布比正态分布更难拟合。
- 我们可以看到,在非缩放版本中有 64 项,计算 P(S_T=x) 的预期误差非常小,小于 0.0001%。
- 将分布集中在 T 处的期望值周围非常重要,12stds 左右对称。 我做了一个版本,其中a和b不对称,残差不均匀分布。直觉上,你会采取 a=0+,但它不会产生理想的结果。*S_T残差是针对 S_T>0 的值计算的,因为这是不可能的,我们不关心小于 0 的值。
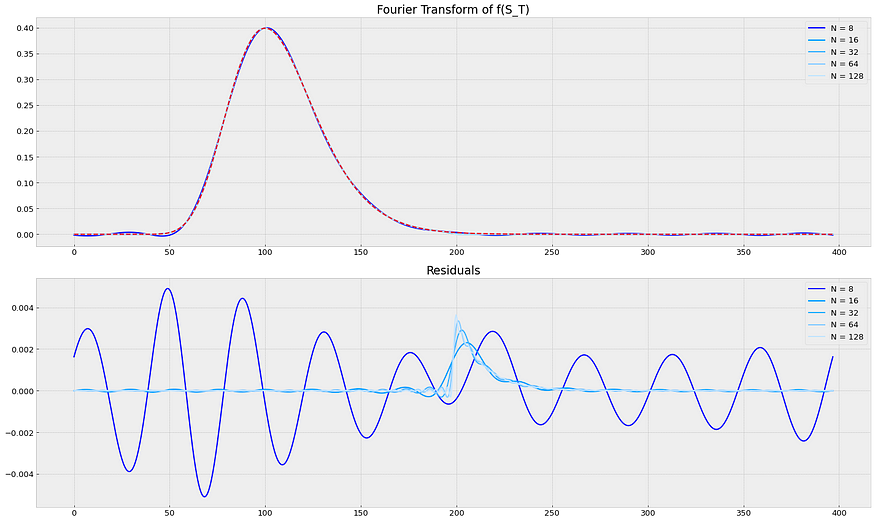
a=1e-8 的S_T密度,在残差处表现出不良性质。来源:笔记本
4.2 限制 — 缺点 — 改进:
- 将前面提到的任何函数近似为傅里叶级数并使用数值积分作为计算 An 和 Bn 的手段没有任何好处。
- 分析计算 An 和 Bn 系数非常重要,因此唯一的数值部分是计算序列。
- 好处在别处。当f(x)没有显式形式并且需要数值积分时,我们可以用特征函数和傅里叶级数半解析地解决问题。
- 如果我们在 Python 中使用 scipy.norm 为带有标准 BS 的选项定价,大约需要 0.06 毫秒。
但是,如果我们解析求解积分 A0、An、Bn 并使用复数版本,我们会得到大约 0.6 毫秒,这是可比的。我们将在第 3 部分中在 Heston 模型中使用它,该模型是此类期权定价的行业标准。
下一篇:第 2 部分
媒介:链接
在下一篇文章中,我们将了解如何将这些知识与特征函数(虚数的使用)结合使用,以使用标准布莱克-斯科尔斯模型计算欧洲看涨期权的值。
相关文章:

傅里叶系列 P1 的定价选项
如果您想了解更多信息,请查看第 2 部分和第 3 部分。 一、说明 这是第一篇文章,我将帮助您获得如何使用这个新的强大工具来解决金融中的半分析问题并取代您的蒙特卡洛方法的直觉。 我们都知道并喜欢蒙特卡洛数字积分方法,但是如果我告诉你你可…...

第二十届北京消防展即将开启,汉威科技即将精彩亮相
10月10日~13日,第二十届中国国际消防设备技术交流展览会,将在北京市顺义区中国国际展览中心新馆隆重举行。该展会由中国消防协会举办,是世界三大消防品牌展会之一,本届主题为“助力产业发展,服务消防救援”。届时将有4…...

mongodb、mysql、redis 区别
MongoDB、MySQL 和 Redis 是三种不同的数据库管理系统,它们在数据存储、访问模型和使用场景方面有一些显著的区别。 1. 数据存储模型: MongoDB:MongoDB 是一种文档数据库,它使用 BSON(Binary JSON)格式来存储数据。数据以文档的形式组织,每个文档可以有不同的字段,文档…...
【Flutter】Flutter Web 开发 如何从 URL 中获取参数值
【Flutter】Flutter Web 开发 如何从 URL 中获取参数值 文章目录 一、前言二、Flutter Web 中的 URL 处理三、如何从 URL 中获取参数四、实际业务中的用法五、完整示例六、总结 一、前言 大家好!我是小雨青年,今天我想和大家分享一下在 Flutter Web 开发…...

【Java 进阶篇】JDBC Statement:执行 SQL 语句的重要接口
在Java应用程序中,与数据库进行交互是一项常见的任务。为了执行数据库操作,我们需要使用JDBC(Java Database Connectivity)来建立与数据库的连接并执行SQL语句。Statement接口是JDBC中的一个重要接口,它用于执行SQL语句…...

Python与数据分析--Pandas操作进阶
目录 1.文件读取方式 1.1.绝对路径读取文件 1.2.相对路径读取文件 2.列表数据操作 2.1.列索引指定 2.2.代码数据对齐 3.创建新CSV文件 4.缺失值处理 4.1.缺失值创建 4.2.缺失值检索 4.3.缺失值查询 4.3.1.isnull()函数判断 4.3.2.notnull()函数判断 4.3.3.any()函数…...

国庆小练习
一、二、三 一、 创建一个双向链表, 将26个英文字母通过头插的方式插入到链表中 通过尾删的方式将数据读取出来并删除。main.c #include <my_head.h> #include "dblink.h"int main(int argc, const char *argv[]) {dblink *h create_head();for…...

springboot单体项目如何拆分成微服务
要将一个Spring Boot单体项目拆分成微服务,可以按照以下步骤进行操作: 识别业务域:首先,需要对单体项目进行业务域的划分。将项目中的功能按照业务领域进行分类,每个业务领域可以成为一个独立的微服务。 定义服务接口…...

解决recovery页面反转的问题
1.前言 在android 10.0的系统rom定制化开发工作中,在系统中recoverv的页面也是相关重要的一部分,在系统recovery ta升级等功能,都是需要recoverv功能的,在某些产品定制化中 在recovery的时候,发现居然旋转了180度&…...
)
如何使用nuScenes数据集格式的单帧数据推理(以DETR3D为例)
【请尊重原创!转载和引用文章内容务必注明出处!未经许可上传到某文库或其他收费阅读/下载网站赚钱的必追究责任!】 无论是mmdetection3D还是OpenPCDet都只有使用数据集(使用哪个数据集由配置文件里指定)训练和测试的代码,没有使用…...
大语言模型之十三 LLama2中文推理
在《大语言模型之十二 SentencePiece扩充LLama2中文词汇》一文中已经扩充好了中文词汇表,接下来就是使用整理的中文语料对模型进行预训练了。这里先跳过预训练环节。先试用已经训练好的模型,看看如何推理。 合并模型 这一步骤会合并LoRA权重࿰…...

iOS AVAudioSession 详解
iOS AVAudioSession 详解 - 简书 默认没有options,category 7种即可满足条件 - (BOOL)setCategory:(AVAudioSessionCategory)category error:(NSError **)outError API_AVAILABLE(ios(3.0), watchos(2.0), tvos(9.0)) API_UNAVAILABLE(macos); 有optionsÿ…...
26-网络通信
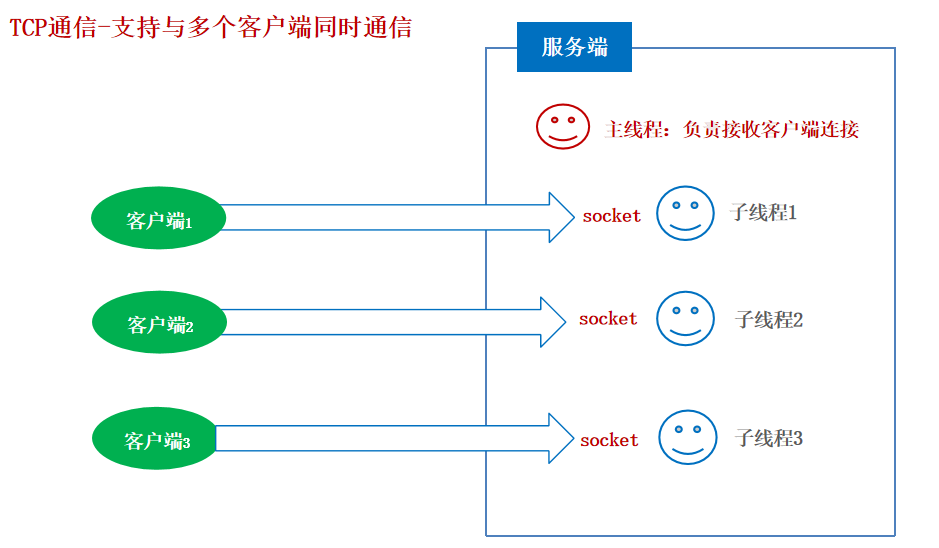
网络通信 什么是网络编程? 可以让设备中的程序与网络上其他设备中的程序进行数据交互(实现网络通信的)。 java.net.包下提供了网络编程的解决方案! 基本的通信架构有2种形式:CS架构( Client客户端/Server服…...

嵌入式Linux应用开发-基础知识-第十九章驱动程序基石③
嵌入式Linux应用开发-基础知识-第十九章驱动程序基石③ 第十九章 驱动程序基石③19.5 定时器19.5.1 内核函数19.5.2 定时器时间单位19.5.3 使用定时器处理按键抖动19.5.4 现场编程、上机19.5.5 深入研究:定时器的内部机制19.5.6 深入研究:找到系统滴答 1…...
一文拿捏SpringMVC的调用流程
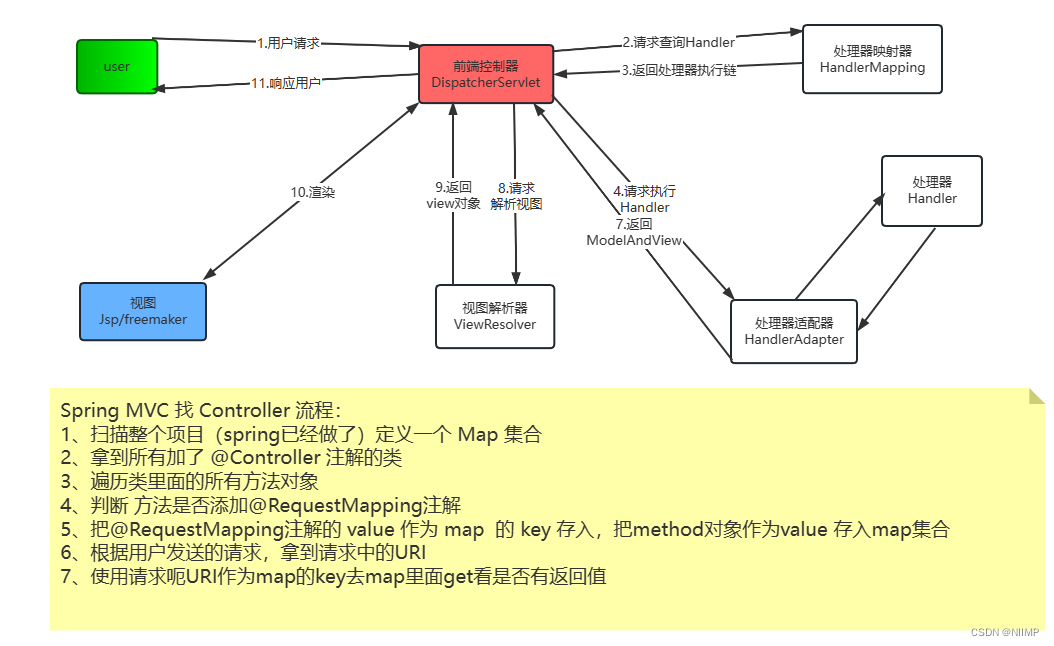
SpringMVC的调用流程 1.核心元素: DispatcherServlet(前端控制器)HandlerMapping(处理器映射器)HandlerAdapter(处理器适配器) ---> Handler(处理器)ViewResolver(视图解析器 )---> view(视图) 2.调用流程 用户发送请求到前端控制器前端控制器接收用户请求…...

一文详解 JDK1.8 的 Lambda、Stream、LocalDateTime
Lambda Lambda介绍 Lambda 表达式(lambda expression)是一个匿名函数,Lambda表达式基于数学中的λ演算得名,直接对应于其中的lambda抽象(lambda abstraction),是一个匿名函数,即没有函数名的函数。 Lambda表达式的结构 一个 Lamb…...

WebSocket实战之二协议分析
一、前言 上一篇 WebSocket实战之一 讲了WebSocket一个极简例子和基础的API的介绍,这一篇来分析一下WebSocket的协议,学习网络协议最好的方式就是抓包分析一下什么就都明白了。 二、WebSocket协议 本想盗一张网络图,后来想想不太好&#x…...
)
LeetCode //C - 208. Implement Trie (Prefix Tree)
208. Implement Trie (Prefix Tree) A trie (pronounced as “try”) or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and s…...
【Python】time模块和datetime模块的部分函数说明
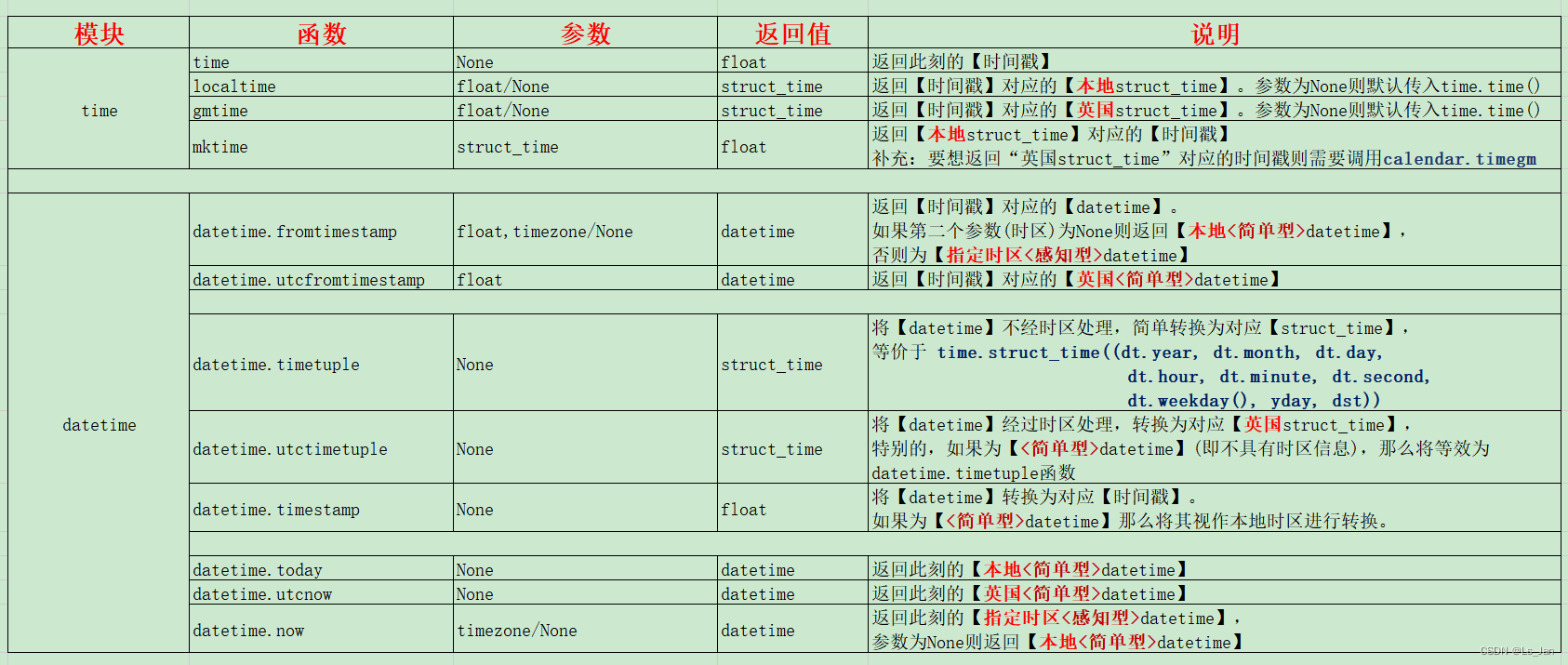
时间戳与日期 在说到这俩模块之前,首先先明确几个概念: 时间戳是个很单纯的东西,没有“时区”一说,因为时间戳本质上是经过的时间。日常生活中接触到的“日期”、“某点某时某分”准确的说是时间点,都是有时区概念的…...

Python 无废话-基础知识元组Tuple详讲
“元组 Tuple”是一个有序、不可变的序列集合,元组的元素可以包含任意类型的数据,如整数、浮点数、字符串等,用()表示,如下示例: 元组特征 1) 元组中的各个元素,可以具有不相同的数据类型,如 T…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
