CF505B Mr. Kitayuta‘s Colorful Graph
Mr. Kitayuta’s Colorful Graph
题面翻译
给出一个 n n n 个点, m m m 条边的无向图,每条边上是有颜色的。有 q q q 组询问
对于第 i i i 组询问,给出点对 u i , v i u_i,v_i ui,vi。求有多少种颜色 c c c 满足:有至少一条 u i u_i ui 到 v i v_i vi 路径,满足该路径上的所有边的颜色都为 c c c
输入格式
第一行两个整数 n , m n,m n,m 分别表示点的个数和边的个数
接下来 m m m 行,每行三个整数 x i , y i , c i x_i,y_i,c_i xi,yi,ci,表示有一条连接点 x i , y i x_i,y_i xi,yi 的边,且该边的颜色为 c i c_i ci
接下来一行一个整数 q q q,表示询问的个数
接下来 q q q 行,每行两个整数 u i , v i u_i,v_i ui,vi,表示一组询问
输出格式
对于每一组询问,在单独的一行输出一个整数,表示满足上述要求的颜色种数
说明与提示
2 ≤ n ≤ 100 2 \le n \le 100 2≤n≤100
1 ≤ m , q ≤ 100 1 \le m,q \le 100 1≤m,q≤100
1 ≤ x i , y i , u i , v i ≤ n 1\le x_i,y_i,u_i,v_i \le n 1≤xi,yi,ui,vi≤n
1 ≤ c i ≤ m 1 \le c_i \le m 1≤ci≤m
感谢 @_Wolverine 提供的翻译
题目描述
Mr. Kitayuta has just bought an undirected graph consisting of $ n $ vertices and $ m $ edges. The vertices of the graph are numbered from 1 to $ n $ . Each edge, namely edge $ i $ , has a color $ c_{i} $ , connecting vertex $ a_{i} $ and $ b_{i} $ .
Mr. Kitayuta wants you to process the following $ q $ queries.
In the $ i $ -th query, he gives you two integers — $ u_{i} $ and $ v_{i} $ .
Find the number of the colors that satisfy the following condition: the edges of that color connect vertex $ u_{i} $ and vertex $ v_{i} $ directly or indirectly.
输入格式
The first line of the input contains space-separated two integers — $ n $ and $ m $ ( $ 2<=n<=100,1<=m<=100 $ ), denoting the number of the vertices and the number of the edges, respectively.
The next $ m $ lines contain space-separated three integers — $ a_{i} $ , $ b_{i} $ ( $ 1<=a_{i}<b_{i}<=n $ ) and $ c_{i} $ ( $ 1<=c_{i}<=m $ ). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if $ i≠j $ , $ (a_{i},b_{i},c_{i})≠(a_{j},b_{j},c_{j}) $ .
The next line contains a integer — $ q $ ( $ 1<=q<=100 $ ), denoting the number of the queries.
Then follows $ q $ lines, containing space-separated two integers — $ u_{i} $ and $ v_{i} $ ( $ 1<=u_{i},v_{i}<=n $ ). It is guaranteed that $ u_{i}≠v_{i} $ .
输出格式
For each query, print the answer in a separate line.
样例 #1
样例输入 #1
4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4
样例输出 #1
2
1
0
样例 #2
样例输入 #2
5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4
样例输出 #2
1
1
1
1
2
提示
Let’s consider the first sample.
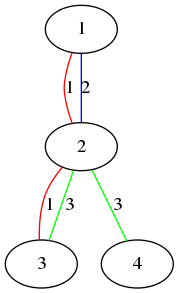 The figure above shows the first sample. - Vertex $ 1 $ and vertex $ 2 $ are connected by color $ 1 $ and $ 2 $ .
The figure above shows the first sample. - Vertex $ 1 $ and vertex $ 2 $ are connected by color $ 1 $ and $ 2 $ .
- Vertex $ 3 $ and vertex $ 4 $ are connected by color $ 3 $ .
- Vertex $ 1 $ and vertex $ 4 $ are not connected by any single color.
思路
(1)并查集
一个二维并查集,一个记录颜色,一个记录点。
(2)Floyed
普通Floyed加一维颜色。数据只有100四维循环不会T。
AC code
(1)并查集
#include<bits/stdc++.h>using namespace std;int fa[1000][1000];
int n, m, t;int find(int x, int i)
{if (fa[x][i] == x) return x;return fa[x][i] = find(fa[x][i], i);
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)fa[i][j] = i; for (int i = 1; i <= m; ++i){int u, v, z;cin >> u >> v >> z;fa[find(u, z)][z] = find(v,z); }cin >> t;while (t--){int u, v, ans = 0;cin >> u >> v;for(int i = 1; i <= m;i++)if (find(u,i) == find(v,i)) ans++; cout << ans << endl;}return 0;
}
(2)Floyed
#include<bits/stdc++.h>using namespace std;int a[101][101][101];int main()
{int n, m;cin >> n >> m;for(int i = 1; i <= m; i++){int u, v, q;cin >> u >> v >> q;a[u][v][q] = 1;a[v][u][q] = 1;}for (int k = 1; k <= n; k++)for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)for (int c = 1; c <= m; c++)if (a[i][k][c] == 1 && a[k][j][c] == 1)a[i][j][c] = 1;int q;cin >> q;for (int i = 1; i <= q; i++){int u, v;cin >> u >> v;int sum = 0;for(int j = 1; j <= m; j++)if(a[u][v][j] == 1)sum++;cout << sum << endl;}return 0;
}相关文章:

CF505B Mr. Kitayuta‘s Colorful Graph
Mr. Kitayuta’s Colorful Graph 题面翻译 给出一个 n n n 个点, m m m 条边的无向图,每条边上是有颜色的。有 q q q 组询问 对于第 i i i 组询问,给出点对 u i , v i u_i,v_i ui,vi。求有多少种颜色 c c c 满足:有至…...
c#设计模式-结构型模式 之 组合模式
🚀简介 组合模式又名部分整体模式,是一种 结构型设计模式 ,是用于把一组相似的对象当作一个 单一的对象 。组合模式 依据树形结构来组合对象 ,用来表示部分以及整体层,它可以让你将对象组合成树形结构,并且…...

【Rust日报】2023-09-30 使用Rust做web抓取
CockroachDB 用rust重新实现 嘿,伙计们,我在 Rust 中实现了一个分布式 SQL 数据库。它就像 CockroachDB 和谷歌Google Spanner。告诉我你的想法。 注意: 这不是生产级别的数据库,这是一个以学习为目的的项目。有许多特性,但是缺少…...
【密评】商用密码应用安全性评估从业人员考核题库(三)
商用密码应用安全性评估从业人员考核题库(三) 国密局给的参考题库5000道只是基础题,后续更新完5000还会继续更其他高质量题库,持续学习,共同进步。 501 多项选择题 《个人信息保护法》要求个人信息处理者应当采取哪些…...

MySQL进阶_查询优化和索引优化
文章目录 第一节、索引失效案例1.1 数据准备1.2 全值匹配我最爱1.3 最佳左前缀法则 第一节、索引失效案例 可以从以下维度对数据库进行优化: 索引失效、没有充分利用到索引–索引建立关联查询太多JOIN (设计缺陷或不得已的需求)–SQL优化服务器调优及各个参数设置…...

Hadoop2复安装过程详细步骤
1、在vmware中更改了虚拟机的网络类型,--->NAT方式,(虚拟交换机的ip可以从vmvare的edit-->vertual network editor看到) 2、根据这个交换机(网关)的地址,来设置我们的客户端windows7的ip&…...

【Java-LangChain:面向开发者的提示工程-7】文本扩展
第七章 文本扩展 扩展是将短文本(例如一组说明或主题列表)输入到大型语言模型中,让模型生成更长的文本(例如基于某个主题的电子邮件或论文)。这种应用是一把双刃剑,好处例如将大型语言模型用作头脑风暴的伙…...
竞赛 基于设深度学习的人脸性别年龄识别系统
文章目录 0 前言1 课题描述2 实现效果3 算法实现原理3.1 数据集3.2 深度学习识别算法3.3 特征提取主干网络3.4 总体实现流程 4 具体实现4.1 预训练数据格式4.2 部分实现代码 5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习机器视觉的…...

从技能需求到就业前景,了解前端和后端开发的优缺点和个人选择
文章目录 每日一句正能量一、引言前端开发后端开发 二、两者的对比分析三、技能转换和跨领域工作四:介绍全栈开发后记 每日一句正能量 命运决定的不是你的人生,能决定你人生的只有自己。 一、引言 前端和后端是Web开发中两个不可或缺的领域。前端开发主…...

Flutter笔记:AnimationMean、AnimationMax 和 AnimationMin 三个类的用法
Flutter笔记 AnimationMean、AnimationMax 和 AnimationMin三个类的用法 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/…...
华为云云耀云服务器L实例评测|云耀云服务器L实例部署Gogs服务器
华为云云耀云服务器L实例评测|云耀云服务器L实例部署Gogs服务器 一、云耀云服务器L实例介绍1.1 云耀云服务器L实例简介1.2 云耀云服务器L实例特点 二、Gogs介绍2.1 Gogs简介2.2 Gogs特点 三、本次实践介绍3.1 本次实践简介3.2 本次环境规划 四、远程登录华为云云耀云…...
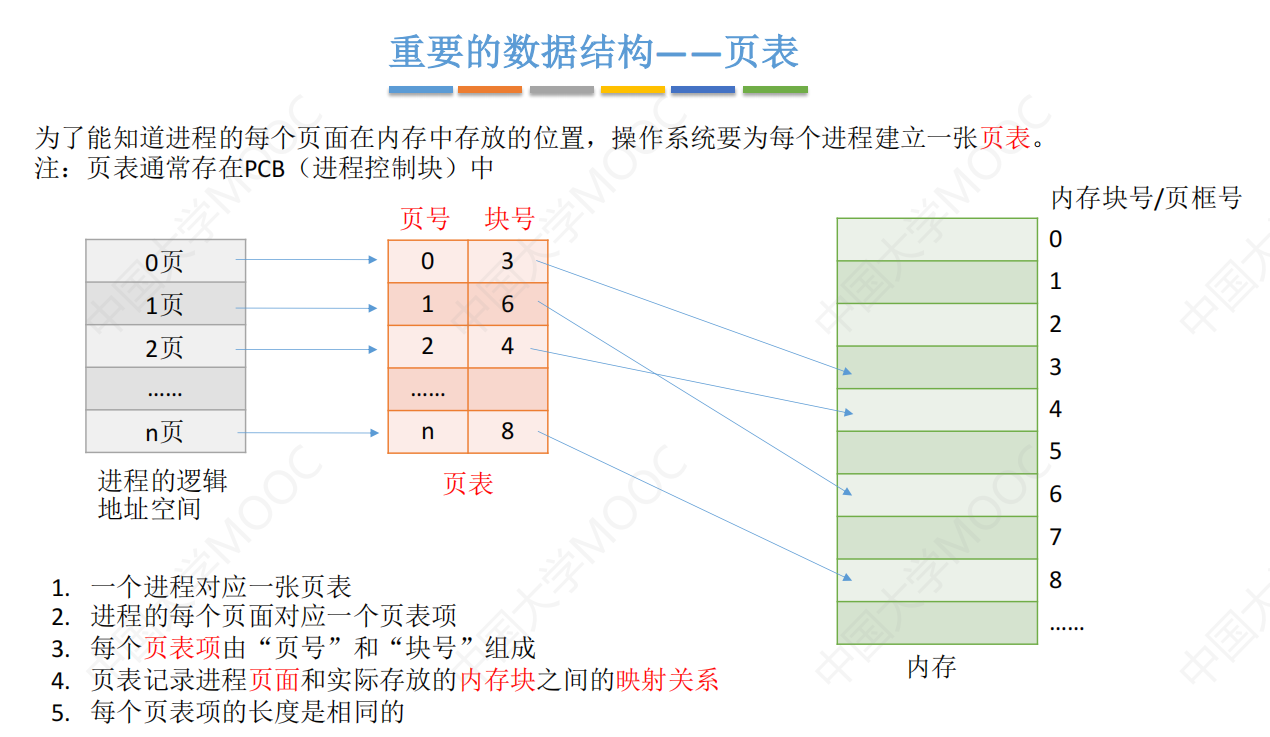
操作系统--分页存储管理
一、概念介绍 分页存储:一是分内存地址,二是分逻辑地址。 1.分内存地址 将内存空间分为一个个大小相等的分区。比如,每个分区4KB。 每个分区就是一个“页框”,每个页框有个编号,即“页框号”,“页框号”…...

【算法练习Day10】有效的括号删除字符串中的所有相邻重复项逆波兰表达式求值
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 有效的括号删除字符串中的所…...

10.1 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、自动驾驶一周资讯 - 苹果汽车项目泡汤?纵目科技IPO终止,腾讯与岚图汽车合作升级,158亿元现金收购比亚迪“史上最大”并购案 自动驾驶一周资讯 - 苹果汽车…...

Redis中Set类型的操作
Set的结构与list相似,但底层存储结构是hashtable,因此它的值是唯一的,同时添加的顺序与保存的顺序并不一致。每一个Set类型的key中可以存储2^32-1个元素。 一、应用场景 1、保存用户的收藏 在小说网站中保存用户的收藏,收藏 的小…...
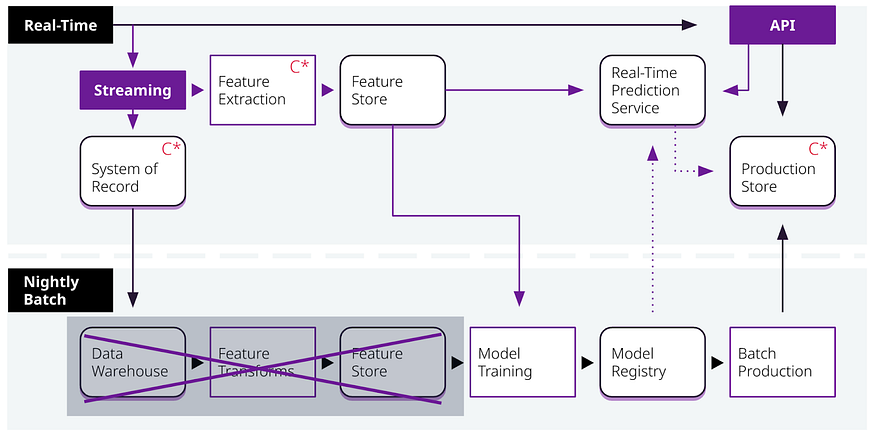
正确完成实时 AI
发表于 构建真实世界的实时 AI 一、说明 我们知道,当前的AI进展是扎根于历史数据,这就造成一个事实,模型总是赶不上实时进展,模型的洞察力不够尖锐,或者,时间损失等,本篇对这一系列AI的短板展开…...

深度学习笔记之线性代数
深度学习笔记之线性代数 一、向量 在数学表示法中,向量通常记为粗体小写的符号(例如,x,y,z)当向量表示数据集中的样本时,它们的值具有一定的现实意义。例如研究医院患者可能面临的心脏病发作风…...

Python与Scrapy:构建强大的网络爬虫
网络爬虫是一种用于自动化获取互联网信息的工具,在数据采集和处理方面具有重要的作用。Python语言和Scrapy框架是构建强大网络爬虫的理想选择。本文将分享使用Python和Scrapy构建强大的网络爬虫的方法和技巧,帮助您快速入门并实现实际操作价值。 一、Pyt…...

kind 安装 k8s 集群
在某些时候可能需要快速的部署一个k8s集群用于测试,不想部署复杂的k8s集群环境,这个时候我们就可以使用kind来部署一个k8s集群了,下面是使用kind部署的过程 一、安装单节点集群 1、下载kind二进制文件 [rootlocalhost knid]# curl -Lo ./kin…...

Leetcode 2871. Split Array Into Maximum Number of Subarrays
Leetcode 2871. Split Array Into Maximum Number of Subarrays 1. 解题思路2. 代码实现 题目链接:2871. Split Array Into Maximum Number of Subarrays 1. 解题思路 这一题实现上其实还是比较简单的,就是一个贪婪算法,主要就是思路上需要…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
