COCI2022-2023#1 Neboderi
P9032 [COCI2022-2023#1] Neboderi
题目大意
有一个长度为 n n n的序列 h i h_i hi,你需要从中选择一个长度大于等于 k k k的子区间 [ l , r ] [l,r] [l,r],使得 g × ( h l + h l + 1 + ⋯ + h r ) g\times (h_l+h_{l+1}+\cdots+h_r) g×(hl+hl+1+⋯+hr)最小,其中 g = gcd ( h l , h l + 1 , … , h r ) g=\gcd(h_l,h_{l+1},\dots,h_r) g=gcd(hl,hl+1,…,hr)。
1 ≤ k ≤ n ≤ 1 0 6 , 1 ≤ h i ≤ 1 0 6 1\leq k\leq n\leq 10^6,1\leq h_i\leq 10^6 1≤k≤n≤106,1≤hi≤106
题解
当确定了 l l l时, gcd ( h l , h l + 1 , … , h r ) \gcd(h_l,h_{l+1},\dots,h_r) gcd(hl,hl+1,…,hr)随着 r r r的增大而减小。
每当 gcd \gcd gcd减小时,其 gcd \gcd gcd相对于原来的 gcd \gcd gcd肯定有若干个质因数的次数减小。那么,对于一个确定的 l l l, gcd ( h l , h l + 1 , … , h r ) \gcd(h_l,h_{l+1},\dots,h_r) gcd(hl,hl+1,…,hr)的取值不会超过 log a l \log a_l logal个数。
先用 S T ST ST表维护区间 gcd \gcd gcd。枚举 l l l,在二分每一段 g c d gcd gcd值相等的区间并取该区间的右端点作为 r r r来更新答案。
设 v v v为 a i a_i ai的最大值,则时间复杂度为 O ( n log n log v ) O(n\log n\log v) O(nlognlogv)。
当然,这是跑不满的,而且时限为 2.50 s 2.50s 2.50s,所以可以过。
code
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1000000;
int n,k,now,v[N+5],lg[N+5],f[N+5][20];
long long ans=0,sum[N+5];
int gcd(int i,int j){while(j){i%=j;swap(i,j);}return i;
}
int gt(int l,int r){int x=lg[r-l+1];return gcd(f[l][x],f[r-(1<<x)+1][x]);
}
int to(int w,int be,int hv){int l=be+1,r=n,mid;while(l<=r){mid=l+r>>1;if(gt(w,mid)>=hv) l=mid+1;else r=mid-1;}return l-1;
}
int main()
{scanf("%d%d",&n,&k);lg[0]=-1;for(int i=1;i<=n;i++){lg[i]=lg[i/2]+1;scanf("%d",&v[i]);sum[i]=sum[i-1]+v[i];f[i][0]=v[i];}for(int i=1;i<=19;i++){for(int j=1;j<=n-(1<<i-1);j++){f[j][i]=gcd(f[j][i-1],f[j+(1<<i-1)][i-1]);}}for(int l=1,r;l<=n-k+1;l++){now=gt(l,l+k-1);r=to(l,l+k-1,now);while(r<=n){ans=max(ans,gt(l,r)*(sum[r]-sum[l-1]));if(r==n) break;now=gt(l,r+1);r=to(l,r+1,now);}}printf("%lld",ans);return 0;
}
相关文章:

COCI2022-2023#1 Neboderi
P9032 [COCI2022-2023#1] Neboderi 题目大意 有一个长度为 n n n的序列 h i h_i hi,你需要从中选择一个长度大于等于 k k k的子区间 [ l , r ] [l,r] [l,r],使得 g ( h l h l 1 ⋯ h r ) g\times (h_lh_{l1}\cdotsh_r) g(hlhl1⋯hr)最小&…...

由于找不到d3dx9_43.dll无法继续执行此代码怎么解决?全面解析d3dx9_43.dll
在使用计算机过程中,我们可能会遇到各种各样的问题。其中之一就是d3dx9_43.dll文件丢失的问题。这个问题通常会出现在运行某些应用程序或游戏时,导致程序无法正常启动或运行。那么,如何解决这个问题呢?小编将为您提供一些解决方案…...

Linux--网络编程-字节序
进程间的通信: 管道、消息队列、共享内存、信号、信号量。 特点:都依赖于linux内核。 缺陷:无法多机通信。 一、网络编程: 1、地址:基于网络,ip地址端口号。 端口号作用: 一台拥有ip地址的主机…...

python实现http/https拦截
python实现http拦截 前言:为什么要使用http拦截一、技术调研二、技术选择三、使用方法前言:为什么要使用http拦截 大多数爬虫玩家会直接选择API请求数据,但是有的网站需要解决扫码登录、Cookie校验、数字签名等,这种方法实现时间长,难度高。需求里面不需要高并发,有没有…...
农产品团购配送商城小程序的作用是什么
农产品覆盖稻麦油蛋等多种细分类目,各地区经营商家众多,随着人们生活品质提升,对食物的要求也在提升,绿色无污染无激素的农产品往往受到不少人喜爱,而在销售中,也有不少人选择自建商城线上经营。 通过【雨…...

使用van-dialog二次封装微信小程序模态框
由于微信小程序的wx.showModal不支持富文本内容,无法实现更灵活的展示效果,故需要进行二次封装 实现思路:使用van-dialog以及微信小程序的rich-text实现 代码如下: // index.wxml <van-dialoguse-slottitle"提示"s…...
生鲜蔬果同城配送社区团购小程序商城的作用是什么
生鲜蔬果行业作为市场主要支撑之一,从业商家众多的同时消费者也从不缺,尤其对中高城市,生鲜蔬果除了传统线下超市、市场经营外,线上更是受到大量消费者信任,而很多商家也是自建了生鲜蔬果商城多场景生意经营。 那么通…...
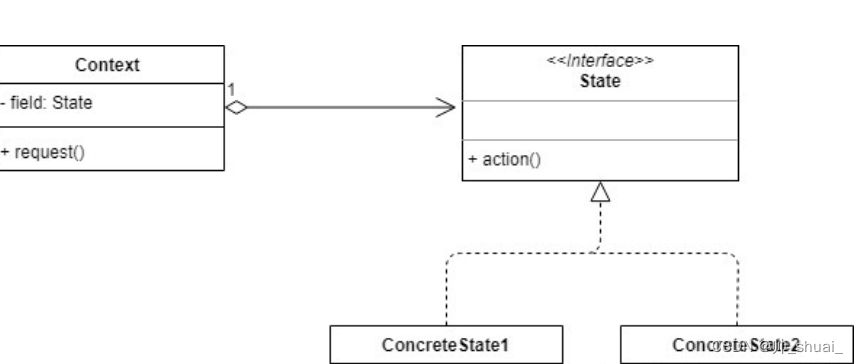
Unity实现设计模式——状态模式
Unity实现设计模式——状态模式 状态模式最核心的设计思路就是将对象的状态抽象出一个接口,然后根据它的不同状态封装其行为,这样就可以实现状态和行为的绑定,最终实现对象和状态的有效解耦。 在实际开发中一般用到FSM有限状态机的实现&…...

差分数组的应用技巧
前缀和技巧 针对的算法场景是不需要对原始数组进行修改的情况下,频繁查询某个区间的累加和。 差分数组 主要适用场景是频繁对原始数组的某个区间的元素进行增减。 相关题目 1094. 拼车 1109. 航班预订统计 370. 区间加法 # 1094. 拼车 class Solution:def carPool…...
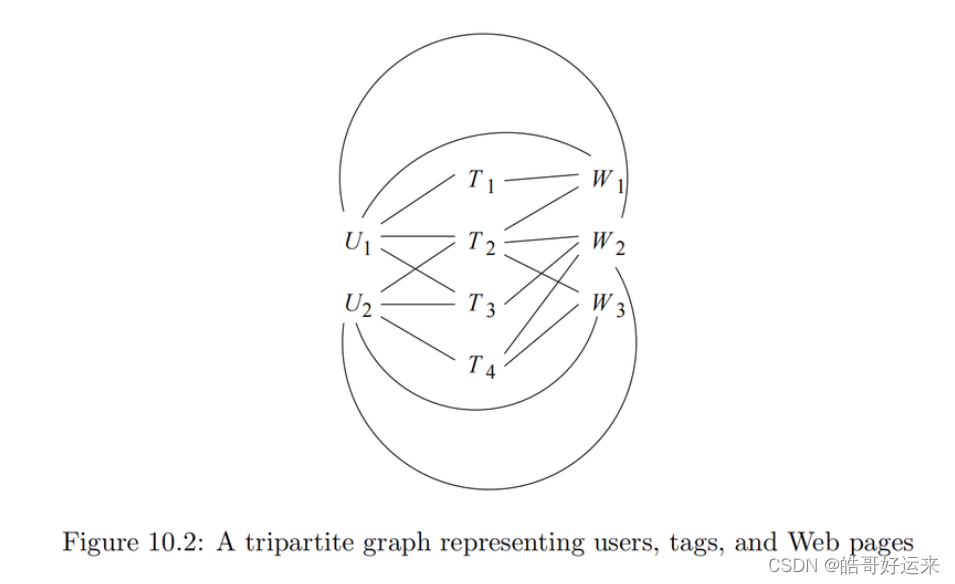
斯坦福数据挖掘教程·第三版》读书笔记(英文版)Chapter 10 Mining Social-Network Graphs
来源:《斯坦福数据挖掘教程第三版》对应的公开英文书和PPT。 Chapter 10 Mining Social-Network Graphs The essential characteristics of a social network are: There is a collection of entities that participate in the network. Typically, these entiti…...

DFS:842. 排列数字
给定一个整数 nn,将数字 1∼n1∼n 排成一排,将会有很多种排列方法。 现在,请你按照字典序将所有的排列方法输出。 输入格式 共一行,包含一个整数 nn。 输出格式 按字典序输出所有排列方案,每个方案占一行。 数据…...

pytorch之nn.Conv1d详解
自然语言处理中一个句子序列,一维的,所以使用Conv1d...

H5生成二维码
H5生成二维码: 1.引入js库,可自行点击链接复制使用 <script type"text/javascript" src"http://static.runoob.com/assets/qrcode/qrcode.min.js"></script>2.加入二维码占位区HTML <div id"qrCode">…...

Three.js加载360全景图片/视频
Three.js加载360全景图片/视频 效果 原理 将全景图片/视频作为texture引入到three.js场景中将贴图与球形网格模型融合,将球模型当做成环境容器使用处理视频时需要以dom为载体,加载与控制视频动作每次渲染时更新当前texture,以达到视频播放效…...

北大硕士7年嵌入式学习经验分享
阶段 1 大一到大三这个阶段我与大多数学生相同: 学习本专业知识(EE专业),学习嵌入式软件开发需要的计算机课程(汇编原理,计算机组成原理,操作系统,C语言等),…...

华为鸿蒙手表开发之动态生成二维码
华为鸿蒙手表开发之动态生成二维码 前言: 最近入职新公司,由于之前的哥们临时离职,走得很突然,所以没有任何交接和文档,临时顶上公司手表应用的上架,更换了新的密钥和key之后重新测试功能和流程ÿ…...
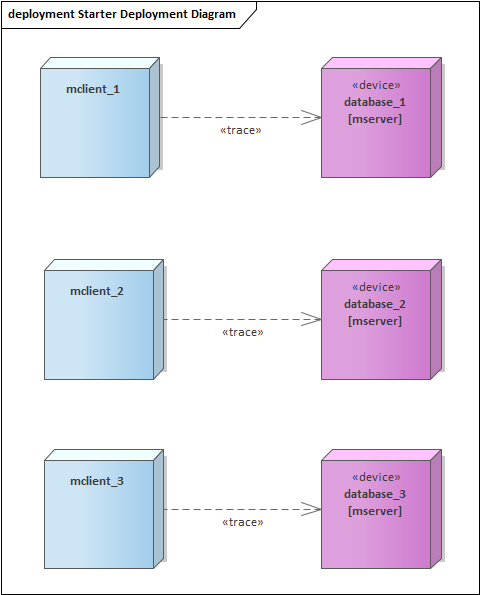
2023-09-28 monetdb-databae的概念和作用-分析
摘要: 每个数据库对于db,schema以及user,role都有一套自己的设计, 不同数据库间对于相同名字的东西例如database和schema可以说南辕北辙, 例如mysql中schema其实是database的同义词. 本文分析monetdb的database的概念和作用 database的概念和作用: 和mysql的database完全不同…...

2024级199管理类联考之数学基础(上篇)
管理类考试介绍 管理综合200分,时间3小时 数学:75分/25题,是拉开差距的核心模块 问题求解题:15个,5选一条件充分性判断:10个,结合两个条件选择答案 条件一充分,条件二不充分:A条件一不充分,条件二充分:B条件一充分,条…...
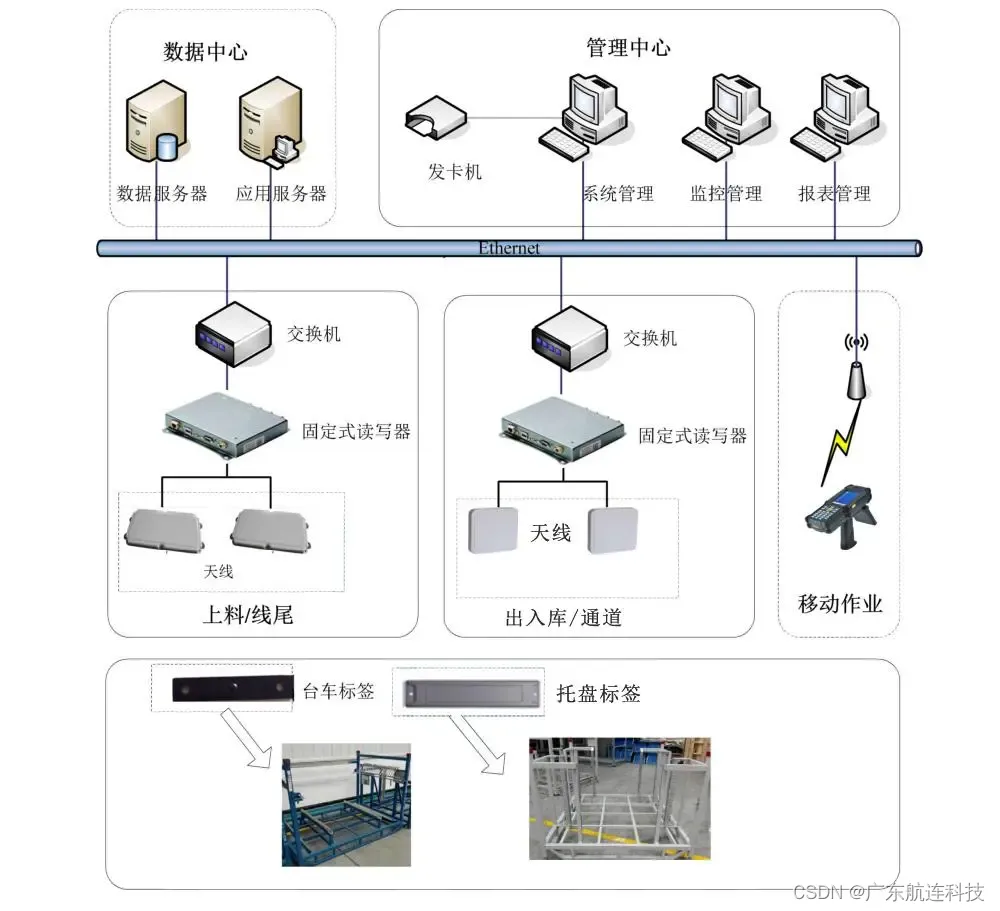
RFID技术引领汽车零部件加工新时代
RFID技术的兴起引领了汽车零部件加工领域的新时代,作为一种利用无线电频率进行自动识别的技术,RFID技术能够快速、准确地识别物体并获取相关数据,在汽车零部件加工中,RFID技术具有重要的应用价值,可以提高生产效率、降…...
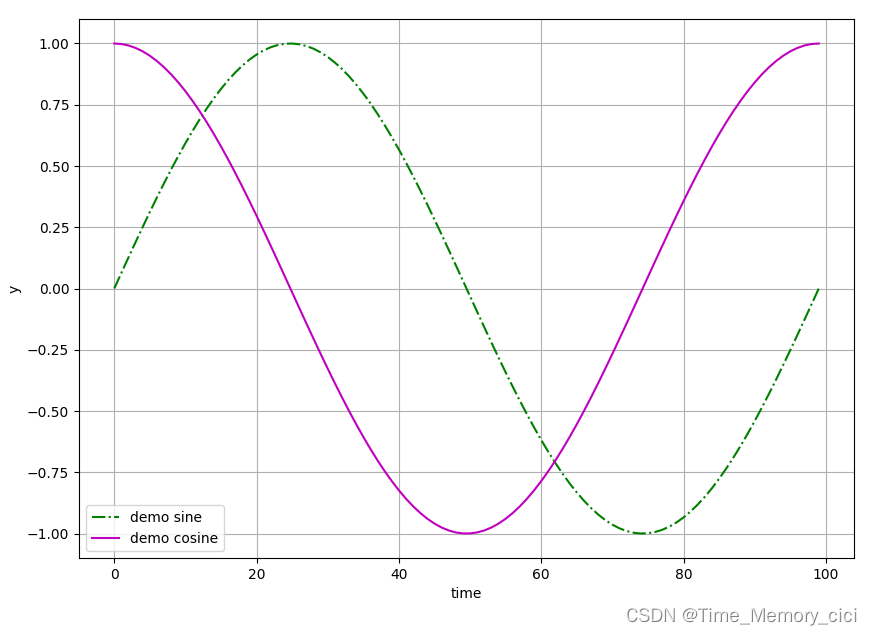
python中使用matplotlib绘图
一、背景 当我们在写python程序时,不可避免的需要将数据可视化,也就是绘制出数据的曲线图,以便我们更直观的观察数据间的变化,和方便对比。此时就要用到matplotlib库了。 matplotlib官方给出的定义是: 翻译过来也就是…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
