背包问题
目录
开端
01背包问题
AcWing 01背包问题
Luogu P2925干草出售
Luogu P1048采药
完全背包问题
AcWing 完全背包问题
Luogu P1853投资的最大效益
多重背包问题
AcWing 多重背包问题 I
AcWing 多重背包问题 II
Luogu P1776宝物筛选
混合背包问题
AcWing 混合背包问题
Luogu P1833樱花
二维费用背包问题
AcWing 二维费用的背包问题
Luogu P1507NASA的食物计划
分组背包问题
AcWing 分组背包问题
Luogu P1757 通天之分组背包
开端
关于背包问题,嗯一直学不明白,暑假咸的没事又拾起来学了一下,跟着这位大佬整理的思路(背包九讲——全篇详细理解与代码实现-CSDN博客),对背包的思想有了一定清晰的理解,大佬的文章有些长,所以跟着自己的思路再整理一下。
为了方便统一,先定义一下
c[i]:表示代价
w[i]:表示价值
dp[i][j]:表示前i个物品花费代价为j的可以获得的最大代价
p[i]:表示第i种物品最多有p[i]件
01背包问题
定义:
dp[i][j]:表示前i个物品恰放入一个容量为j的背包下可以获得的最大代价子问题第i1件物品状态:
①不选:dp[i][j]=dp[i-1][j]②选:dp[i][j]=dp[i][j-c[i]]+w[i]状态转移方程:
dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i])优化空间复杂度:
O(V*N)
for(int i=1;i<=n;i++)for(int j=c[i];j<=V;j--)dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i]);O(V)
for(int i=1;i<=n;i++)for(int j=V;j>=c[i];j++)dp[j]=max(dp[j],dp[j-c[i]]+w[i]);关于顺序和逆序:
逆序表示:dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])转移过来的 顺序表示:dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i][j],dp[i][j-c[i]]+w[i])转移过来的初始化问题:
①要求恰好装满:dp[i]=-∞,dp[0]=0;②只要求价值最大:dp[i]=0;
AcWing 01背包问题

const int N = 1010;
int c[N], w[N], dp[N];
inline void solve()
{int N, V;cin >> N >> V;for (int i = 1; i <= N; i++)cin >> c[i] >> w[i];for (int i = 1; i <= N; i++)for (int j = V; j >= c[i]; j--)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << dp[V] << endl;
}Luogu P2925干草出售
const int N = 5e4 + 10;
int w[N], dp[N];
inline void solve()
{int C, H;cin >> C >> H;for (int i = 1; i <= H; i++)cin >> w[i];for (int i = 1; i <= H; i++)for (int j = C; j >= w[i]; j--)dp[j] = max(dp[j], dp[j - w[i]] + w[i]);cout << dp[C] << endl;
}Luogu P1048采药
const int N = 1010;
int c[N], w[N], dp[N];
inline void solve()
{int T, M;cin >> T >> M;for (int i = 1; i <= M; i++)cin >> c[i] >> w[i];for (int i = 1; i <= M; i++)for (int j = T; j >= c[i]; j--)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << dp[T] << endl;
}完全背包问题
定义:
dp[i][j]:表示前i种物品恰放入一个容量为j的背包下可以获得的最大代价子问题第i种物品状态:
①不选该种物品:dp[i][j]=dp[i-1][j]; ②选不同件该种物品:选0件、1件、2件……k件:dp[i][j]=dp[i-1][j-c[i]*k]+w[i]*k;状态转移方程:
dp[i][j]=max(dp[i-1][j-c[i]*k]+w[i]*k) 0<=c[i]*k<=j优化空间复杂度:
O(N*∑(V/c[i]))
for(int i=1;i<=n;i++)for(int j=c[i];j<=V;j++)for(int k=0;c[i]*k<=j;k++)dp[i][j]=max(dp[i][j],dp[i-1][j-c[i]*k]+w[i]*k); # 第一个参数,因为k=0时就相当于dp[i-1][j];O(V*N)转化为01背包问题
for(int i=1;i<=n;i++)for(int j=c[i];j<=j;j++)dp[j]=max(dp[j],dp[j-c[i]]+w[i]); //等价于dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i]);(不取该物品,取不同件);关于顺序和逆序:
逆序表示:dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])转移过来的 顺序表示:dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i])转移过来的初始化问题:
①要求恰好装满:dp[i]=-∞,dp[0]=0;②只要求价值最大:dp[i]=0;
AcWing 完全背包问题

const int N = 1010;
int c[N], w[N], dp[N];
inline void solve()
{int N, V;cin >> N >> V;for (int i = 1; i <= N; i++)cin >> c[i] >> w[i];for (int i = 1; i <= N; i++)for (int j = c[i]; j <= V; j++)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << dp[V] << endl;
}Luogu P1853投资的最大效益
const int N = 1e6 + 10;
int c[N], w[N], dp[N];
inline void solve()
{int s, n, d;cin >> s >> n >> d;for (int i = 1; i <= d; i++)cin >> c[i] >> w[i];while (n--){for (int i = 1; i <= d; i++)for (int j = c[i]; j <= s; j++)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);s += dp[s];}cout << s << endl;
}
int main(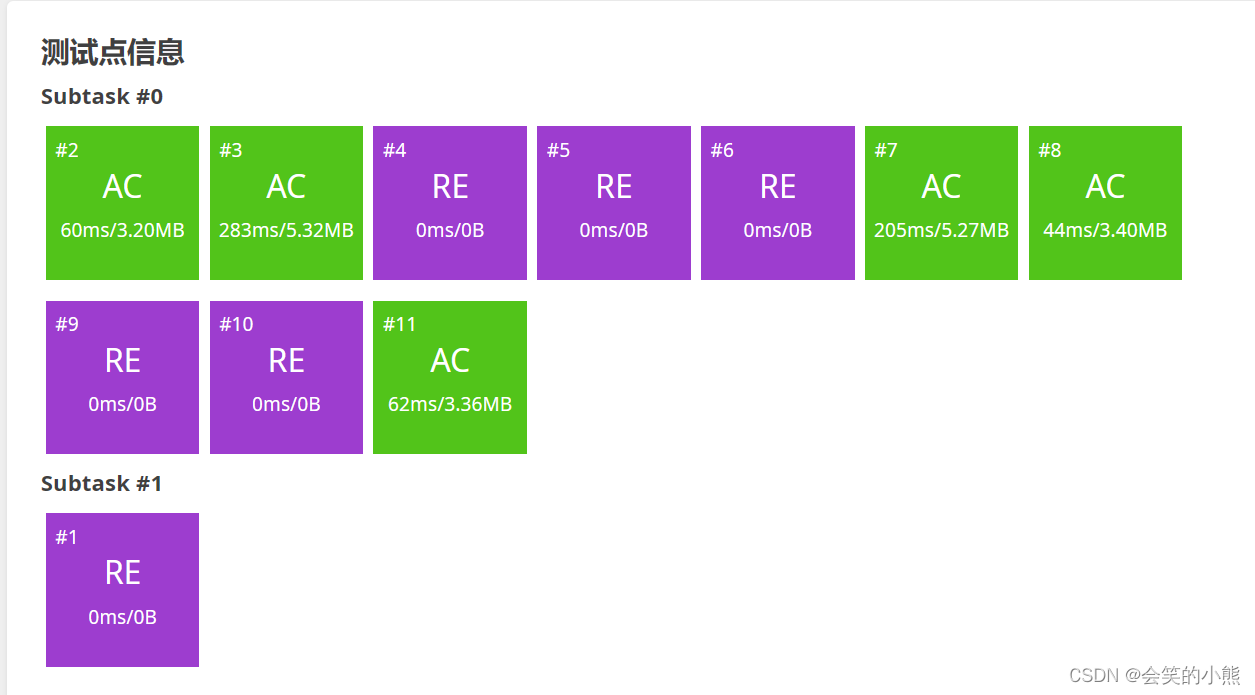
这个题目有个小坑
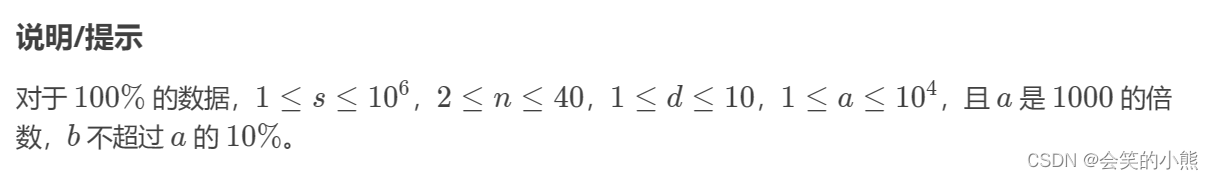
所以要做一下处理:除以1000防止爆空间
const int N = 1e6 + 10;
int c[N], w[N], dp[N];
inline void solve()
{int s, n, d;cin >> s >> n >> d;for (int i = 1; i <= d; i++)cin >> c[i] >> w[i];while (n--){for (int i = 1; i <= d; i++)for (int j = c[i] / 1000; j <= s / 1000; j++)dp[j] = max(dp[j], dp[j - c[i] / 1000] + w[i]);s += dp[s / 1000];}cout << s << endl;
}多重背包问题
定义:
dp[i][j]:表示前i种物品恰放入一个容量为j的背包下可以获得的最大代价子问题第i种物品状态:
①不选该种物品:dp[i][j]=dp[i-1][j]; ②选不同件该种物品:选1件、2件……p[i]件:dp[i][j]=dp[i-1][j-c[i]*k]+w[i]*k;状态转移方程:
dp[i][j]=max(dp[i-1][j-c[i]*k]+w[i]*k) 0<=k<=p[i]转化为01背包问题:
方法一:O(V*∑p[i])
for(int i=1;i<=n;i++)for(int j=V;j>=c[i];j--)for(int k=1;c[i]*k<=j&&k<=p[i];k++)dp[j]=max(dp[j],dp[j-c[i]*k]+w[i]*k); # 第一个参数,因为k=0时就相当于dp[i-1][j];方法二:二进制优化O(N*log(p)*V)
for (int i = 1; i <= N; i++){int a, b, s;cin >> a >> b >> s;int k = 1;while (k <= s) //0……2^k-1部分的系数1,2,4,8……{cnt++;c[cnt] = k * a;w[cnt] = k * b;s -= k;k *= 2;}if (s > 0) //2^k……s部分的系数 s-2^k{cnt++;c[cnt] = s * a;w[cnt] = s * b;}}N = cnt; //更新总数量for (int i = 1; i <= N; i++) //01背包问题for (int j = V; j >= c[i]; j--)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);for (int i = 1; i <= n; i++){cin >> c[i] >> w[i] >> p[i];int s = min(p[i], W / w[i]);for (int k = 1; s > 0; k <<= 1){k = min(k, s);s -= k;for (int j = W; j >= k * w[i]; j--){dp[j] = max(dp[j], dp[j - k * w[i]] + k * c[i]);}}}初始化问题:
①要求恰好装满:dp[i]=-∞,dp[0]=0;②只要求价值最大:dp[i]=0;
方法一:
AcWing 多重背包问题 I

const int N = 110;
int c[N], w[N], p[N], dp[N];
inline void solve()
{int N, V;cin >> N >> V;int cnt = 0;for (int i = 1; i <= N; i++)cin >> c[i] >> w[i] >> p[i];for (int i = 1; i <= N; i++)for (int j = V; j >= c[i]; j--)for (int k = 1; c[i] * k <= j && k <= p[i]; k++)dp[j] = max(dp[j], dp[j - c[i] * k] + w[i] * k);cout << dp[V] << endl;
}方法二:
AcWing 多重背包问题 II

const int N = 20010; //注意初始化,否则会越界
int c[N], w[N], dp[N];
inline void solve()
{int N, V;cin >> N >> V;int cnt = 0;for (int i = 1; i <= N; i++){int a, b, s;cin >> a >> b >> s;int k = 1;while (k <= s) //0……2^k-1部分的系数1,2,4,8……{cnt++;c[cnt] = k * a;w[cnt] = k * b;s -= k;k *= 2;}if (s > 0) //2^k……s部分的系数 s-2^k{cnt++;c[cnt] = s * a;w[cnt] = s * b;}}N = cnt; //更新总数量for (int i = 1; i <= N; i++) //01背包问题for (int j = V; j >= c[i]; j--)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << dp[V] << endl;
}Luogu P1776宝物筛选
const int N = 1e6 + 10; // 注意初始化,否则会越界
int c[N], w[N], dp[N];
inline void solve()
{int n, W;cin >> n >> W;int cnt = 0;for (int i = 1; i <= n; i++){int a, b, s;cin >> a >> b >> s;int k = 1;while (k <= s){cnt++;w[cnt] = k * a;c[cnt] = k * b;s -= k;k *= 2;}if (s > 0){cnt++;w[cnt] = s * a;c[cnt] = s * b;}}n = cnt;for (int i = 1; i <= n; i++)for (int j = W; j >= c[i]; j--)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);cout << dp[W] << endl;
}简化
const int N = 1e6 + 10; // 注意初始化,否则会越界
int c[N], w[N], p[N], dp[N];
inline void solve()
{int n, W;cin >> n >> W;for (int i = 1; i <= n; i++){cin >> c[i] >> w[i] >> p[i];int s = min(p[i], W / w[i]);for (int k = 1; s > 0; k <<= 1){k = min(k, s);s -= k;for (int j = W; j >= k * w[i]; j--){dp[j] = max(dp[j], dp[j - k * w[i]] + k * c[i]);}}}cout << dp[W] << endl;
}混合背包问题
01背包、完全背包、多重背包的混合状态转移:
for (int i = 1; i <= N; i++){cin >> c[i] >> w[i] >> p[i];// 01背包if (p[i] == -1)for (int j = V; j >= c[i]; j--)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);// 完全背包else if (p[i] == 0)for (int j = c[i]; j <= V; j++)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);// 多重背包二进制优化else{int s = min(p[i], V / c[i]);for (int k = 1; s > 0; k <<= 1){k = max(k, s);s -= k;for (int j = V; j >= k * c[i]; j--)dp[j] = max(dp[j], dp[j - k * c[i]] + k * w[i]);}}}
AcWing 混合背包问题

const int N = 1e6 + 10; // 注意初始化,否则会越界
int c[N], w[N], p[N], dp[N];
inline void solve()
{int N, V;cin >> N >> V;for (int i = 1; i <= N; i++){cin >> c[i] >> w[i] >> p[i];// 01背包if (p[i] == -1)for (int j = V; j >= c[i]; j--)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);// 完全背包else if (p[i] == 0)for (int j = c[i]; j <= V; j++)dp[j] = max(dp[j], dp[j - c[i]] + w[i]);//或将完全背包转化为多重01背包s=V/c[i]// 多重背包二进制优化else{int s = min(p[i], V / c[i]);for (int k = 1; s > 0; k <<= 1){k = min(k, s);s -= k;for (int j = V; j >= k * c[i]; j--)dp[j] = max(dp[j], dp[j - k * c[i]] + k * w[i]);}}}cout << dp[V] << endl;
}Luogu P1833樱花
const int N = 1e6 + 10; // 注意初始化,否则会越界
int c[N], w[N], p[N], dp[N];
inline void solve()
{int m1, m2, s1, s2, N;scanf("%d:%d %d:%d %d", &m1, &s1, &m2, &s2, &N);int V = m2 * 60 + s2 - m1 * 60 - s1;for (int i = 1; i <= N; i++){cin >> c[i] >> w[i] >> p[i];int s;if (p[i] == 0) // 完全转化为多重s = V / c[i];elses = min(p[i], V / c[i]);for (int k = 1; s > 0; k <<= 1){k = min(k, s);s -= k;for (int j = V; j >= k * c[i]; j--)dp[j] = max(dp[j], dp[j - k * c[i]] + k * w[i]);}}cout << dp[V] << endl;
}二维费用背包问题
定义:每件物品需要同时花费两种不同的代价
dp[i][j][k]:表示前i种物品付出两种代价分别最大为j和k时可获得的最大价值状态转移方程:
dp[i][j][k]=max(dp[i-1][j][k],dp[i-1][j-c[i]][k-m[i]]+w[i])01背包代码(完全背包、多重背包可以类比)
for(int i=1;i<=n;i++)for(int j=V;j>=c[i];j--)for(int k=M;k>=m[i];k--)dp[j][k]=max(dp[j][k],dp[j-c[i]][k-m[i]]+w[i]);
AcWing 二维费用的背包问题

const int N = 1010; // 注意初始化,否则会越界
int c[N], w[N], m[N], dp[N][N];
inline void solve()
{int N, V, M;cin >> N >> V >> M;for (int i = 1; i <= N; i++){cin >> c[i] >> m[i] >> w[i];for (int j = V; j >= c[i]; j--)for (int k = M; k >= m[i]; k--)dp[j][k] = max(dp[j][k], dp[j - c[i]][k - m[i]] + w[i]);}cout << dp[V][M] << endl;
}Luogu P1507NASA的食物计划
const int N = 1010; // 注意初始化,否则会越界
int c[N], w[N], m[N], dp[N][N];
inline void solve()
{int V, M, N;cin >> V >> M >> N;for (int i = 1; i <= N; i++){cin >> c[i] >> m[i] >> w[i];for (int j = V; j >= c[i]; j--)for (int k = M; k >= m[i]; k--)dp[j][k] = max(dp[j][k], dp[j - c[i]][k - m[i]] + w[i]);}cout << dp[V][M] << endl;
}分组背包问题
定义:
dp[k][j]:表示前k组物品花费代价j能取得的最大价值子问题第k组物品状态:
①不选该组物品:dp[k][j]=dp[k-1][j]; ②选该组物品:dp[k][j]=dp[k-1][j-c[i]+w[i]] 物品i属于k组状态转移方程:
dp[k][j]=max(dp[k-1][j],dp[k-1][j-c[i]]+w[i])模板:
for (int k = 1; k <= N; k++){int s;cin >> s; // 第k组的物品数量for (int i = 1; i <= s; i++)cin >> c[i] >> w[i]; // 组中每个物品i的属性for (int j = V; j >= 0; j--)for (int i = 1; i <= s; i++) // 保证每组物品只能选一个,可以覆盖之前组内物品最优解的来取最大值if (j >= c[i])dp[j] = max(dp[j], dp[j - c[i]] + w[i]);}
AcWing 分组背包问题

const int N = 110; // 注意初始化,否则会越界
int c[N], w[N], m[N], dp[N];
inline void solve()
{int N, V;cin >> N >> V;for (int k = 1; k <= N; k++){int s;cin >> s; // 第k组的物品数量for (int i = 1; i <= s; i++)cin >> c[i] >> w[i]; // 组中每个物品i的属性for (int j = V; j >= 0; j--)for (int i = 1; i <= s; i++) // 保证每组物品只能选一个,可以覆盖之前组内物品最优解的来取最大值if (j >= c[i])dp[j] = max(dp[j], dp[j - c[i]] + w[i]);}cout << dp[V] << endl;
}Luogu P1757 通天之分组背包
const int N = 110; // 注意初始化,否则会越界
const int M = 1010; // 注意初始化,否则会越界
int c[M], w[M], dp[M];
int g[N][N], b[M]; // g[k][i]表示小组k种第i个物品的编号,b[k]表示小组k的物品+1;
inline void solve()
{int N, V;cin >> V >> N;int t = 0, k = 0;for (int i = 1; i <= N; i++){cin >> c[i] >> w[i] >> k;t = max(t, k); // 求小组的组数b[k]++; // 小组k的物品+1;g[k][b[k]] = i; // 小组k中第b[k]个物品的编号为i;}for (int k = 1; k <= t; k++)for (int j = V; j >= 0; j--)for (int i = 1; i <= b[k]; i++)if (j >= c[g[k][i]])dp[j] = max(dp[j], dp[j - c[g[k][i]]] + w[g[k][i]]);cout << dp[V] << endl;
}
相关文章:

背包问题
目录 开端 01背包问题 AcWing 01背包问题 Luogu P2925干草出售 Luogu P1048采药 完全背包问题 AcWing 完全背包问题 Luogu P1853投资的最大效益 多重背包问题 AcWing 多重背包问题 I AcWing 多重背包问题 II Luogu P1776宝物筛选 混合背包问题 AcWing 混合背包问题…...
 | 抽象类和抽象接口)
JavaSE | 初始Java(十一) | 抽象类和抽象接口
抽象类概念 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的, 如果 一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类 在 Java 中,一个…...
产品经理如何科学的进行需求调研?
导语:作为产品经理,需求调研是开展工作的重要环节之一。科学、有效地进行需求调研不仅可以帮助产品经理更好地了解用户需求,还能指导产品设计和功能开发,提升产品的竞争力。本文将介绍几种科学的方法和技巧,帮助产品经…...
AI智能问答系统源码/AI绘画商业系统/支持GPT联网提问/支持Midjourney绘画
一、AI创作系统 SparkAi创作系统是基于国外很火的ChatGPT进行开发的AI智能问答系统和AI绘画系统。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图…...
玩具玩偶配送经营商城小程序的作用是什么?
玩具玩偶是小孩子们喜欢的产品,其市场需求度很高,以前玩具店里总是不缺乏客户,但现在随着人们生活品牌提升及消费形式改变,无论玩具厂商还是门店经销商都面对着不少痛点: 如拓客引流难、线上销售经营难、营销难、分销…...
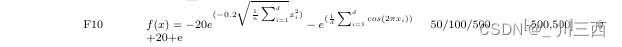
latex表格内容换行
问题描述: 在用latex表格中编写公式时,可能出现公式太长,表格中后面的内容不能在文档中呈现,如下图1,故要进行行内内容的换行,使内容呈现完全而传统的\换行后,换行内容会顶格,如图2。 解决方…...

2023 牛客国庆day4 【10.2训练补题】
目录 B-Basic Gcd Problem(素数筛快速幂) H-Harder Gcd Problem(素数) B-Basic Gcd Problem(素数筛快速幂) 打表找规律发现答案为 (n质因子数目)^c #include<bits/stdc.h> using namespace std;…...
获取都为空)
android的USB开发时 mUsbManager.getDeviceList()获取都为空
类提供的主要方法有: getDeviceList() 获得设备列表,返回的是一个HashMap.;hasPermission(UsbDevice device) 判断你的应用程序是否有接入此USB设备的权限,如果有则返回真,否则返回false.openDevice(UsbDevice device) 打开USB设…...

SpringCloud Alibaba - Seata 部署 TC 服务,并集成微服务
目录 一、Seata 架构 1.1、Seata 架构重要角色 1.2、部署 TC 服务 1.2.1、前言 1.2.2、下载 seata-server 包,解压 1.2.3、修改配置 1.2.4、在 nacos 中添加配置 1.2.5、创建数据库表 1.2.6、启动 TC 服务 1.3、微服务集成 Seata 1.3.1、引入依赖 1.3.2、…...

Java基础面试,接口和抽象类的区别?
接口和抽象类的区别? 抽象类可以存在普通成员函数,而接口中只能存在public abstract 方法。抽象类中的成员变量可以是各种类型的,而接口中的成员变量只能是public static final类型的.抽象类只能继承一个,接口可以实现多个。 接…...

《视觉 SLAM 十四讲》V2 第 4 讲 李群与李代数 【什么样的相机位姿 最符合 当前观测数据】
P71 文章目录 4.1 李群与李代数基础4.1.3 李代数的定义4.1.4 李代数 so(3)4.1.5 李代数 se(3) 4.2 指数与对数映射4.2.1 SO(3)上的指数映射罗德里格斯公式推导 4.2.2 SE(3) 上的指数映射SO(3),SE(3),so(3),se(3)的对应关系 4.3 李代数求导与扰动模型4.3.2 SO(3)上的李代数求导…...
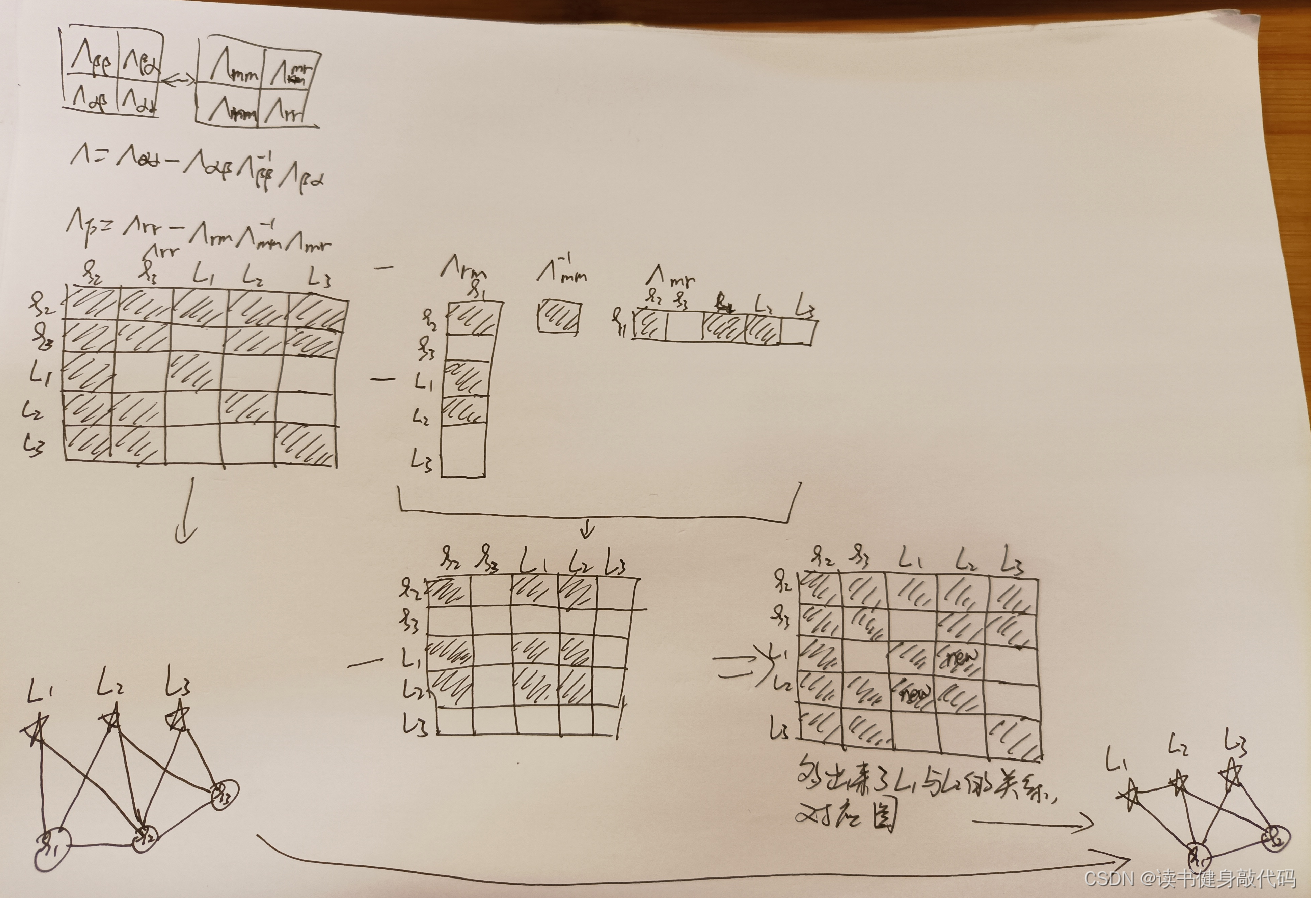
【深蓝学院】手写VIO第4章--基于滑动窗口算法的 VIO 系统:可观性和 一致性--笔记
0. 内容 T1. 参考SLAM14讲P247直接可写,注意 ξ 1 , ξ 2 \xi_1,\xi_2 ξ1,ξ2之间有约束(关系)。 套用舒尔补公式: marg掉 ξ 1 \xi_1 ξ1之后,信息被传递到 L 1 和 L 2 L_1和L_2 L1和L2之间了。 T2....

mfc 动态加载dll库,Mat转CImage,读ini配置文件,鼠标操作,在edit控件上画框,调试信息打印
动态加载dll库 h文件中添加 #include "mydll.h" #ifdef UNICODE //区分字符集 #define LoadLibrary LoadLibraryW #else #define LoadLibrary LoadLibraryA #endif // !UNICODEtypedef double(*mydllPtr)(int, int);类内添加: mydllPtr m_mydll; cpp…...
索尼 toio™应用创意开发征文|检测工业平台震动
虽然索尼toio Q宝机器人主要是为儿童教育娱乐开发的,但我认为它在工业等领域也有一定应用潜力。例如,工业领域经常会有某些平面在实际作业中持续震动,导致零件过疲劳、平台失去稳定等问题。而这样的平台往往位于机器内部,从外部很…...
【已解决】 Expected linebreaks to be ‘LF‘ but found ‘CRLF‘.
问题描述 团队都是用mac,只有我自己是windows,启动项目一直报错 Expected linebreaks to be ‘LF‘ but found ‘CRLF‘. 但我不能因为自己的问题去改团队配置,也尝试过该vscode配置默认是LF还是报错 思路 看文章vscode如何替换所有文件的…...

Java8 Lambda.stream.sorted() 方法使用浅析分享
文章目录 Java8 Lambda.stream.sorted() 方法使用浅析分享sorted() 重载方法一升序降序 sorted() 重载方法二升序降序多字段排序 mock代码 Java8 Lambda.stream.sorted() 方法使用浅析分享 本文主要分享运用 Java8 中的 Lambda.stream.sorted方法排序的使用! sorted…...
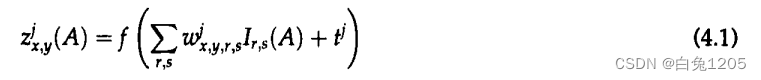
Neural Networks for Fingerprint Recognition
Neural Computation ( IF 3.278 ) 摘要: 在采集指纹图像数据库后,设计了一种用于指纹识别的神经网络算法。当给出一对指纹图像时,算法输出两个图像来自同一手指的概率估计值。在一个实验中,神经网络使用几百对图像进行训练&…...

ChatGPT推出全新功能,引发人工智能合成声音担忧|百能云芯
人工智能AI科技企业OpenAI公司25日宣布,其聊天应用程序ChatGPT如今具备「看、听、说」能力,至少能够理解口语、用合成语音回应并且处理图像;但专家忧心,以假乱真与深度伪造的乱象可能变本加厉。 国家广播公司新闻网(NBC News)报导…...
Java 实现遍历一个文件夹,文件夹有100万数据,获取到修改时间在2天之内的数据
目录 1 需求2 实现1(第一种方法)2 实现2 (推荐使用这个,快)3 实现3(推荐) 1 需求 现在有一个文件夹,里面会一直存数据,动态的存数据,之后可能会达到100万&am…...

持续集成部署-k8s-命令行工具:基础命令的使用
持续集成部署-k8s-命令行工具:基础命令的使用 1. 资源类型与别名2. 资源操作2.1 创建对象2.2 显示和查找资源2.3 更新资源2.4 修补资源2.5 编辑资源2.6 scale 资源2.7 删除资源3. 格式化输出1. 资源类型与别名 资源类型缩写别名clusterscomponentstatusescsconfigmapscmdaemon…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
