数据挖掘实验(一)数据规范化【最小-最大规范化、零-均值规范化、小数定标规范化】
一、数据规范化的原理
数据规范化处理是数据挖掘的一项基础工作。不同的属性变量往往具有不同的取值范围,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果。为了消除指标之间由于取值范围带来的差异,需要进行标准化处理。将数据按照比例进行缩放,使之落入一个特定的区域,便于进行综合分析。
1.1.最小-最大规范化
clear;clc;
A = [78 521 602 2863144 -600 -521 224595 -457 468 -128369 596 695 1054190 527 691 2051101 403 470 2487146 413 435 2571];new = input("请输入需要映射到的新区间。输入格式示例:[0,1]\n");
new_mi = new(1);
new_mx = new(2);
% 计算每列的最小值和最大值
min_vals = min(A);
max_vals = max(A);% 对每个元素进行最小-最大规范化
normalized_A = (A - min_vals) ./ (max_vals - min_vals)* (new_mx - new_mi) + new_mi;;disp(normalized_A);
MATLAB支持广播机制的,在进行矩阵运算时,可以自动扩展维度较小的矩阵,使其与维度较大的矩阵相匹配,从而实现逐元素的运算。
在MATLAB中,要实现广播机制,需要满足以下条件:
- 运算的两个矩阵相应维度的大小要么相同,要么其中一个为1。
- 运算符必须是逐元素的运算符,如.*、./、.\、.^等,不能是矩阵乘法*或矩阵除法/。
- 如果运算的两个矩阵都是列向量或者行向量,那么它们可以直接进行逐元素运算,无需扩展维度。
disp函数是MATLAB中用于在命令行窗口中显示输出的函数。它可以显示各种类型的数据,包括数字、字符串、矩阵等。
A = [78 521 602 2863144 -600 -521 224595 -457 468 -128369 596 695 1054190 527 691 2051101 403 470 2487146 413 435 2571];
new = input("请输入需要映射到的新区间。输入格式示例:[0,1]\n");
new_mi = new(1);
new_mx = new(2);
B = mapminmax(A',new_mi ,new_mx)';
fprintf("\n经过最小最大规范化后:\n");
disp(B)Matlab有一个现成的函数可以实现最小-最大规范化,它就是 mapminmax() 函数
[Y,PS] = mapminmax(X,YMIN,YMAX)其中X是要规范化的矩阵或向量,YMIN和YMAX是指定的区间端点(默认为-1和1),Y是规范化后的矩阵或向量,PS是一个结构体,包含了规范化所用的参数,如最小值、最大值、缩放因子等。如果要对另一个矩阵或向量应用相同的规范化参数,可以使用 mapminmax(‘apply’,X,PS) 函数。
代码运行结果
输入的新区间范围为[0,1]:
原数据:
A =78 521 602 2863144 -600 -521 224595 -457 468 -128369 596 695 1054190 527 691 2051101 403 470 2487146 413 435 2571请输入需要映射到的新区间。输入格式示例:[0,1]
[0,1]经过最小最大规范化后:
B =0.0744 0.9373 0.9235 1.00000.6198 0 0 0.85090.2149 0.1196 0.8133 00 1.0000 1.0000 0.56371.0000 0.9423 0.9967 0.80410.2645 0.8386 0.8150 0.90930.6364 0.8470 0.7862 0.9296
1.2零-均值规范化
clear;clc;%% 数据存入A
A=[78 521 602 2863
144 -600 -521 2245
95 -457 468 -1283
69 596 695 1054
190 527 691 2051
101 403 470 2487
146 413 435 2571];A_mean=mean(A); % mean求的是每列的均值
A_std=std(A); % std求的是每列的标准差
[n,m]=size(A);
B=(A-A_mean)./A_std;fprintf("原数据:");
disp(A);
fprintf("经过零均值规范化后:");
disp(B);
代码运行结果
原数据:
A =78 521 602 2863144 -600 -521 224595 -457 468 -128369 596 695 1054190 527 691 2051101 403 470 2487146 413 435 2571经过零均值规范化后:
B =-0.9054 0.6359 0.4645 0.79810.6047 -1.5877 -2.1932 0.3694-0.5164 -1.3040 0.1474 -2.0783-1.1113 0.7846 0.6846 -0.45691.6571 0.6478 0.6752 0.2348-0.3791 0.4018 0.1521 0.53730.6504 0.4216 0.0693 0.5956
clear;clc;%% 数据存入A
A=[78 521 602 2863
144 -600 -521 2245
95 -457 468 -1283
69 596 695 1054
190 527 691 2051
101 403 470 2487
146 413 435 2571];B = zscore (A); % 沿每列计算标准差fprintf("原数据:");
disp(A);
fprintf("经过零均值规范化后:");
disp(B);
Matlab有一个现成的函数可以实现零-均值规范化,它就是 zscore() 函数1。这个函数可以计算一个数组或向量中元素的标准差,并返回每个元素的 z 分数,即对数据进行中心化和缩放处理,使其均值为 0,标准差为 1。
Z = zscore (X) % 计算X沿第一个非单一维度的标准差 Z = zscore (X,flag) % 指定标准差的类型 Z = zscore (X,flag,'all') % 使用X中所有值的均值和标准差 Z = zscore (X,flag,dim) % 指定沿哪个维度计算 Z = zscore (X,flag,vecdim) % 指定沿多个维度计算 [Z,mu,sigma] = zscore ( ___) % 还返回均值和标准差
1.3小数定标规范化
clear;clc;%% 数据存入A
A = [78 521 602 2863144 -600 -521 224595 -457 468 -128369 596 695 1054190 527 691 2051101 403 470 2487146 413 435 2571];mx = max(abs(A)); % 求每列绝对值最大的数mx
len = floor(log10(mx))+1; % 求mx的位数len
B = A ./ (10.^len); % 将A中每个元素除以10^lenfprintf("原数据:\n");
disp(A);
fprintf("经过小数定标规范化:\n");
disp(B);
代码运行结果
原数据:
A =78 521 602 2863144 -600 -521 224595 -457 468 -128369 596 695 1054190 527 691 2051101 403 470 2487146 413 435 2571经过小数定标规范化后:
B =0.0780 0.5210 0.6020 0.28630.1440 -0.6000 -0.5210 0.22450.0950 -0.4570 0.4680 -0.12830.0690 0.5960 0.6950 0.10540.1900 0.5270 0.6910 0.20510.1010 0.4030 0.4700 0.24870.1460 0.4130 0.4350 0.2571
相关文章:

数据挖掘实验(一)数据规范化【最小-最大规范化、零-均值规范化、小数定标规范化】
一、数据规范化的原理 数据规范化处理是数据挖掘的一项基础工作。不同的属性变量往往具有不同的取值范围,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果。为了消除指标之间由于取值范围带来的差异,需要进行标准化处理。将数据…...
C++17中std::filesystem::directory_entry的使用
C17引入了std::filesystem库(文件系统库, filesystem library)。这里整理下std::filesystem::directory_entry的使用。 std::filesystem::directory_entry,目录项,获取文件属性。此directory_entry类主要用法包括: (1).构造函数、…...
C/C++跨平台构建工具CMake入门
文章目录 1.概述2.环境准备2.1 安装编译工具2.2 安装CMake 3.编译一个示例程序总结 1.概述 本人一直对OpenGL的3d渲染很感兴趣,但是苦于自己一直是Android开发,没有机会接触这方面的知识。就在最近吗,机会来了,以前一个做3D渲染的…...
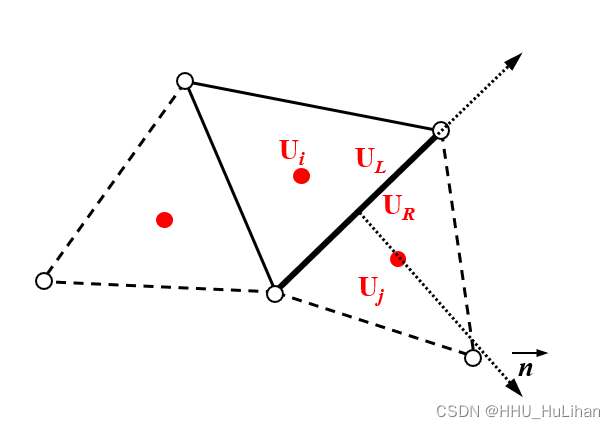
【CFD小工坊】浅水方程的离散及求解方法
【CFD小工坊】浅水方程的离散及求解方法 前言基于有限体积法的方程离散界面通量与源项计算干-湿网格的处理数值离散的稳定性条件参考文献 前言 我们模型的控制方程,即浅水方程组的表达式如下: ∂ U ∂ t ∂ E ( U ) ∂ x ∂ G ( U ) ∂ y S ( U ) U…...

第十四章 类和对象——C++对象模型和this指针
一、成员变量和成员函数分开存储 在C中,类内的成员变量和成员函数分开存储 只有非静态成员变量才属于类的对象上 class Person {public:Person() {mA 0;}//非静态成员变量占对象空间int mA;//静态成员变量不占对象空间static int mB; //函数也不占对象空间&#…...

计算机竞赛 深度学习卫星遥感图像检测与识别 -opencv python 目标检测
文章目录 0 前言1 课题背景2 实现效果3 Yolov5算法4 数据处理和训练5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **深度学习卫星遥感图像检测与识别 ** 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...
java web+Mysql e-life智能生活小区物业管理系统
本项目为本人自己书写,主要服务小区业主和管理人员。 e-life智能生活小区涉及多个方面的智能化和便利化服务: 1. 用户模块:包含基本的登入登出操作,查看个人信息中用户可以查看 自己的个人资料但不可以修改个人信息。 a) 用户…...

AttributeError: module ‘dgl‘ has no attribute ‘batch_hetero‘
DGLWarning: From v0.5, DGLHeteroGraph is merged into DGLGraph. You can safely replace dgl.batch_hetero with dgl.batch...
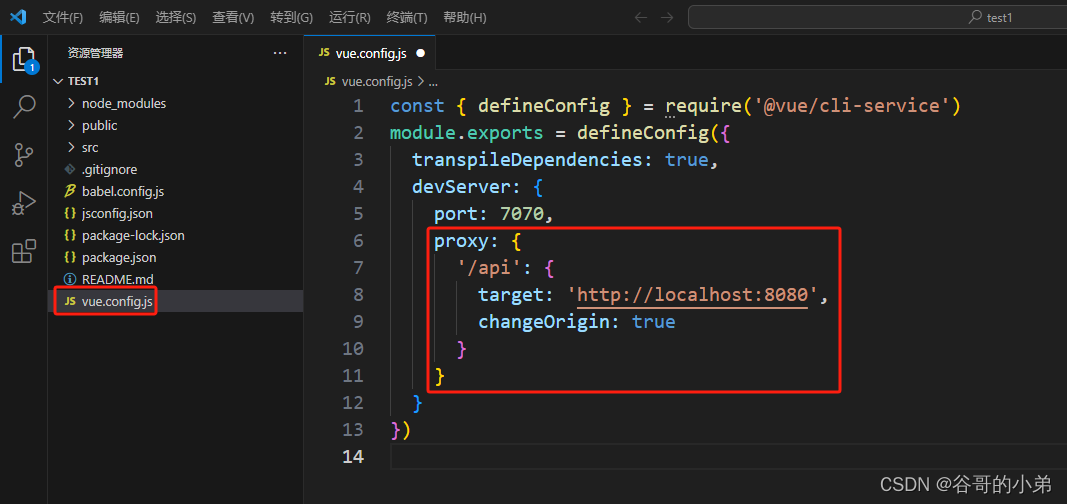
Vue项目搭建图文详解教程
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 预备工作 请在本地创建文件夹用于存放Vue项目,例如:创建HelloWorld文件夹存放即将创建的Vue新项目。 创建Vue项目 首先,请在DOS中将目录…...

SpringMVC处理请求核心流程
一、前言 SpringMVC是一个基于Java的Web框架,它使用MVC(Model-View-Controller)设计模式来处理Web请求。在SpringMVC中,请求处理的核心流程主要包括以下几个步骤: 1、用户发送请求到前端控制器(Dispatche…...

SoloX:Android和iOS性能数据的实时采集工具
SoloX:Android和iOS性能数据的实时采集工具 github地址:https://github.com/smart-test-ti/SoloX 最新版本:V2.7.6 一、SoloX简介 SoloX是开源的Android/iOS性能数据的实时采集工具,目前主要功能特点: 无需ROOT/越狱…...

【知识点随笔分析 | 第五篇】简单介绍什么是QUIC
前言: 随着互联网的快速发展,传统的基于TCP的协议开始显现出一些局限性。TCP在连接建立和拥塞控制方面存在一定的延迟,这可能导致用户在访问网页、观看视频或玩网络游戏时感受到不必要的等待时间。而QUIC作为一种新兴的传输协议,试…...

vscode ssh 远程免密登录开发
存放代码的机器运行 sshd, vscode 所在机器保证可以通过 ssh 登录服务器vscode 机器通过 ssh-keygen 生成 ssh 公私钥对(已有可以忽略)将客户端的 id_rsa.pub 加入到服务器的鉴权队列 cat id_rsa.pub >> authorized_keysvscode 配置ssh登录即可.ctrlp, remote-ssh: open …...
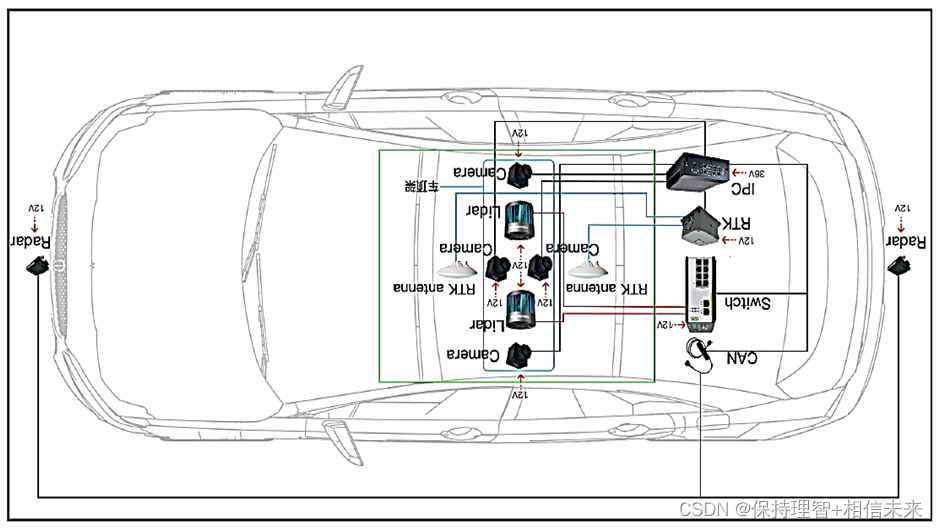
辅助驾驶功能开发-测试篇(2)-真值系统介绍
1 真值系统概述 1.1 真值评测系统核心应用 快速构建有效感知真值,快速完成感知性能评估,快速分析感知性能缺陷。 主要应用场景包括: 1. 感知算法开发验证: 在算法开发周期中,评测结果可以作为测试报告的一部分,体现算法性能的提升。 2. 遴选供应…...

运行程序时msvcr110.dll丢失的解决方法,msvcr110.dll丢失5的个详细解决方法
在使用电脑的过程中,我们经常会遇到各种问题,其中之一就是 msvcr110.dll 丢失的问题。msvcr110.dll 是 Microsoft Visual C Redistributable 的一个组件,用于支持使用 Visual C 编写的应用程序。如果您的系统中丢失了这个文件,您可…...

已解决 Bug——IndexError: index 3 is out of bounds for axis 0 with size 3问题
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页: 🐅🐾猫头虎的博客🎐《面试题大全专栏》 🦕 文章图文并茂🦖…...
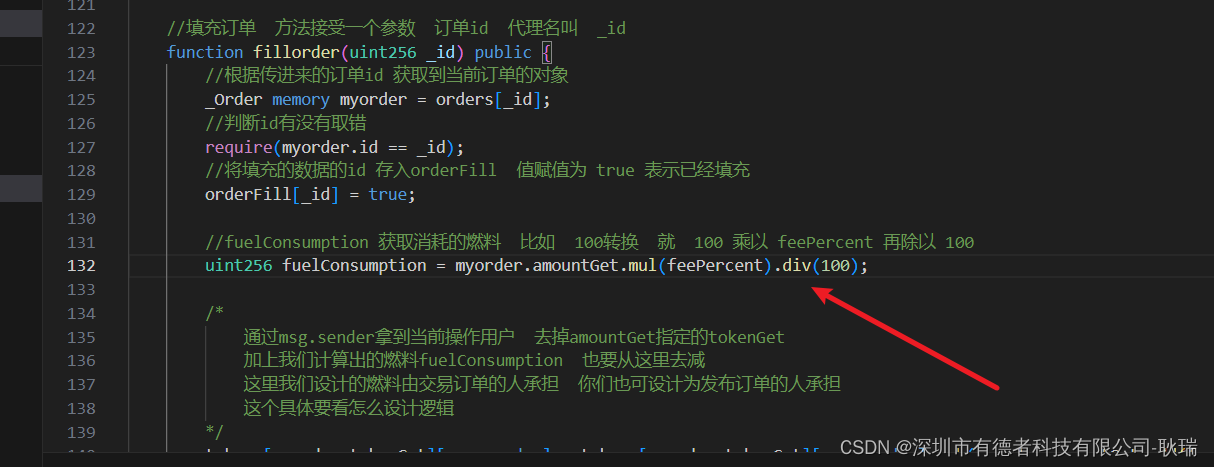
WEB3 solidity 带着大家编写测试代码 操作订单 创建/取消/填充操作
好 在我们的不懈努力之下 交易所中的三种订单函数已经写出来了 但是 我们只是编译 确认了 代码没什么问题 但还没有实际的测试过 这个测试做起来 其实就比较的麻烦了 首先要有两个账号 且他们都要在交易所中有存入 我们还是先将 ganache 的虚拟环境启动起来 然后 我们在项目…...
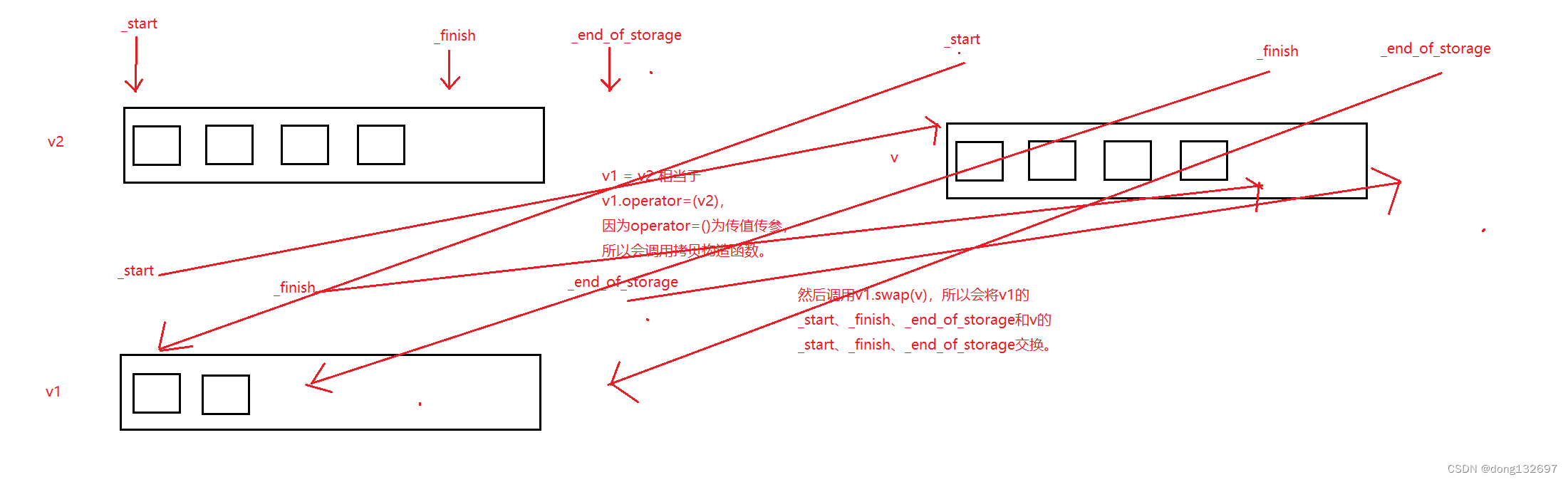
c++-vector
文章目录 前言一、vector介绍二、vector使用1、构造函数2、vector 元素访问3、vector iterator 的使用4、vector 空间增长问题5、vector 增删查改6、理解vector<vector< int >>7、电话号码的字母组合练习题 三、模拟实现vector1、查看STL库源码中怎样实现的vector2…...
十四天学会C++之第二天(函数和库)
1. 函数的定义和调用 在C中,函数是组织和结构化代码的关键工具之一。它们允许您将一段代码封装成一个可重复使用的模块,这有助于提高代码的可读性和维护性。 为什么使用函数? 函数在编程中的作用不可小觑。它们有以下几个重要用途…...

蓝桥杯每日一题2023.10.3
杨辉三角形 - 蓝桥云课 (lanqiao.cn) 题目描述 题目分析 40分写法: 可以自己手动构造一个杨辉三角,然后进行循环,用cnt记录下循环数的个数,看哪个数与要找的数一样,输出cnt #include<bits/stdc.h> using na…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
