C++算法 —— 动态规划(10)二维费用背包
文章目录
- 1、动规思路简介
- 2、一和零
- 3、盈利计划
背包问题需要读者先明白动态规划是什么,理解动规的思路,并不能给刚接触动规的人学习。所以最好是看了之前的动规博客,以及两个背包博客,或者你本人就已经懂得动规了。
1、动规思路简介
动规的思路有五个步骤,且最好画图来理解细节,不要怕麻烦。当你开始画图,仔细阅读题时,学习中的沉浸感就体验到了。
状态表示
状态转移方程
初始化
填表顺序
返回值
动规一般会先创建一个数组,名字为dp,这个数组也叫dp表。通过一些操作,把dp表填满,其中一个值就是答案。dp数组的每一个元素都表明一种状态,我们的第一步就是先确定状态。
状态的确定可能通过题目要求来得知,可能通过经验 + 题目要求来得知,可能在分析过程中,发现的重复子问题来确定状态。还有别的方法来确定状态,但都大同小异,明白了动规,这些思路也会随之产生。状态的确定就是打算让dp[i]表示什么,这是最重要的一步。状态表示通常用某个位置为结尾或者起点来确定。
状态转移方程,就是dp[i]等于什么,状态转移方程就是什么。像斐波那契数列,dp[i] = dp[i - 1] + dp[i - 2]。这是最难的一步。一开始,可能状态表示不正确,但不要紧,大胆制定状态,如果没法推出转移方程,没法得到结果,那这个状态表示就是错误的。所以状态表示和状态转移方程是相辅相成的,可以帮你检查自己的思路。
要确定方程,就从最近的一步来划分问题。
初始化,就是要填表,保证其不越界。像第一段所说,动规就是要填表。比如斐波那契数列,如果要填dp[1],那么我们可能需要dp[0]和dp[-1],这就出现越界了,所以为了防止越界,一开始就固定好前两个值,那么第三个值就是前两个值之和,也不会出现越界。初始化的方式不止这一点,有些问题,假使一个位置是由前面2个位置得到的,我们初始化最一开始两个位置,然后写代码,会发现不够高效,这时候就需要设置一个虚拟节点,一维数组的话就是在数组0位置处左边再填一个位置,整个dp数组的元素个数也+1,让原先的dp[0]变为现在的dp[1],二维数组则是要填一列和一行,设置好这一行一列的所有值,原先数组的第一列第一行就可以通过新填的来初始化,这个初始化方法在下面的题解中慢慢领会。
第二种初始化方法的注意事项就是如何初始化虚拟节点的数值来保证填表的结果是正确的,以及新表和旧表的映射关系的维护,也就是下标的变化。
填表顺序。填当前状态的时候,所需要的状态应当已经计算过了。还是斐波那契数列,填dp[4]的时候,dp[3]和dp[2]应当都已经计算好了,那么dp[4]也就出来了,此时的顺序就是从左到右。还有别的顺序,要依据前面的分析来决定。
返回值,要看题目要求。
背包问题有很多种分类,此篇是关于二维费用背包问题的,优化代码的方法在之前的两篇背包博客的模板题中,此篇就不写了。
2、一和零
474. 一和零

二维费用的背包问题就是原先的背包问题再加一个考虑因素,比如要考虑体积和重量。二维也有01和完全背包,这道题是二维01背包问题。
01背包中,dp[i][j]表示从前i个物品中挑选,总体积不超过j,最大价值的选法。这道题就要再加一维,变成dp[i][j][k],从前i个字符串中挑选,字符0的个数不超过j,字符1的个数不超过k,最大长度的选法。
状态转移方程。其实还是一样的分析。最后一个位置的字符串,如果不选i,那么就看dp[i - 1][j][k];如果选i,i这个字符串有a个0 1以及b个1,所以就看dp[i - 1][j - a][k - b],然后 + 1,并且要求j - a >= 0,k - b >= 0;两个值取max。
初始化时,i为0,则dp[0][j][k]全为0。返回值,因为要从整个字符串数组中挑选,而不是其中某一个最大值,所以返回值是最后一个值。
int findMaxForm(vector<string>& strs, int m, int n) {int len = strs.size();vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(m + 1, vector<int>(n + 1)));for(int i = 1; i <= len; i++){int a = 0, b = 0;for(auto ch : strs[i - 1]){if(ch == '0') a++;else b++;}for(int j = 0; j <= m; j++){for(int k = 0; k <= n; k++){dp[i][j][k] = dp[i - 1][j][k];if(j >= a && k >= b)dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1);}}}return dp[len][m][n];}
但肯定不能这样写,做优化。去掉i这一维,j和k从大到小循环。
int findMaxForm(vector<string>& strs, int m, int n) {int len = strs.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));for(int i = 1; i <= len; i++){int a = 0, b = 0;for(auto ch : strs[i - 1]){if(ch == '0') a++;else b++;}for(int j = m; j >= a; j--){for(int k = n; k >= b; k--){dp[j][k] = max(dp[j][k], dp[j - a][k - b] + 1);}}}return dp[m][n];}
3、盈利计划
879. 盈利计划

给了n和minProFit,group和profit数组,挑选几个人做某一份工作,人数不能超过n,并且利润,也就是profit数组里的被挑选的数,要>= minProFit,选group中第几个元素,利润就是profit数组中第几个元素。每个工作只能选一个,所以就是01背包问题。
让dp[i][j][k]表示从前i个工作中挑选,总人数不超过j,总利润至少为k,总共的选法。
状态转移方程。我们当然还是以最后一个位置i来分析。选择第i个工作,那就看dp[i - 1][j][k];如果选i,那么按照上一个题就是dp[i - 1][j - g[i]],k部分,由于是至少,思路就不一样,如果p[i]小于,那么就正常地看[k - p[i]]位置,如果p[i]大于k,就不能选择k - p[i]的位置了,因为数组下标不能为负数,所以这样写max(0, k - p[i]),如果p[i]更大,那么保证前面至少为0就行。然后这两个数相加。
初始化时dp[0][j][0] = 1。填表顺序要保证i从小到大即可。返回值是最后一个值。
int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p) {const int MOD = 1e9 + 7;int len = g.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1));for(int j = 0; j <= n; j++) dp[j][0] = 1;for(int i = 1; i <= len; i++){for(int j = n; j >= g[i - 1]; j--){for(int k = m; k >= 0; k--){dp[j][k] += dp[j - g[i - 1]][max(0, k - p[i - 1])];dp[j][k] %= MOD;}}}return dp[n][m];}
结束。
相关文章:

C++算法 —— 动态规划(10)二维费用背包
文章目录 1、动规思路简介2、一和零3、盈利计划 背包问题需要读者先明白动态规划是什么,理解动规的思路,并不能给刚接触动规的人学习。所以最好是看了之前的动规博客,以及两个背包博客,或者你本人就已经懂得动规了。 1、动规思路简…...

MySQL数据库正在耗用大量CPU的问题排查
这是一篇实战性的文章,如何处理正在发生的MYSQL服务器CPU飙升的问题,一般情况下,MySQL是不会耗用这么高的CPU的,要么是不走索引的查询,要么是同一时间出现了大量比较耗用资源的查询,不管出现的是哪一种情况…...

php替换字符串里的a变为b
$tempstrstr_replace("\\","/",$tempstr); //把$tempstr中的a替换成b $tempstrstr_replace("a","b",$tempstr);...

黑豹程序员-架构师学习路线图-百科:CSS-网页三剑客
文章目录 1、为什么需要CSS2、发展历史3、什么是CSS4、什么是SASS、SCSS 1、为什么需要CSS 作为网页三剑客的第二,CSS为何需要它,非常简单HTML只能完成页面的展现,但其做出来的页面奇丑无比。 随着网络的普及,人们的要求更高&…...

NUWA论文阅读
论文链接:NUWA: Visual Synthesis Pre-training for Neural visUal World creAtion 文章目录 摘要引言相关工作视觉自回归模型视觉稀疏自注意 方法3D数据表征3D Nearby Self-Attention3D编码器-解码器训练目标 实验实现细节与SOTA比较T2I微调T2V微调V2V微调Sketch-t…...
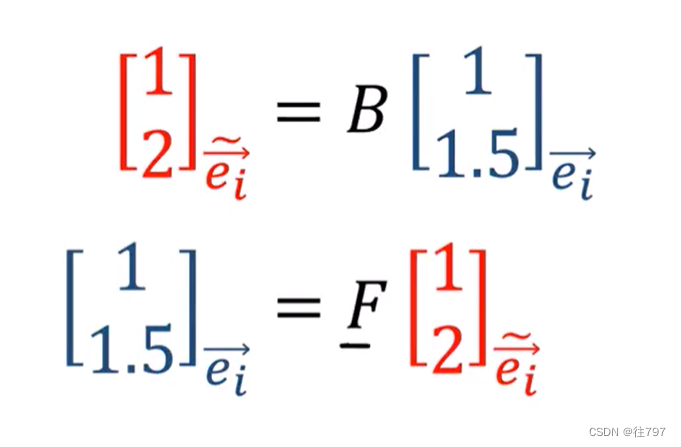
4.Tensors For Beginners-Vector Definition
在上一节,已经了解了前向和后向转换。 什么是向量? 定义1:向量是一个数字列表 这很简洁,也通俗易懂。 现有两个向量: 如果要把这两个向量给加起来,只需把对应位置的元素(组件)给加起来。 而要缩放向量&…...

vertx学习总结5
这章我们讲回调,英文名:Beyond callbacks 一、章节覆盖: 回调函数及其限制,如网关/边缘服务示例所示 未来和承诺——链接异步操作的简单模型 响应式扩展——一个更强大的模型,特别适合组合异步事件流 Kotlin协程——…...

Go,从命名开始!Go的关键字和标识符全列表手册和代码示例!
目录 一、Go的关键字列表和分类介绍关键字在Go中的定位语言的基石简洁与高效可扩展性和灵活性 关键字分类声明各种代码元素组合类型的字面表示基本流程控制语法协程和延迟函数调用 二、Go的关键字全代码示例关键字全代码示例 三、Go的标识符定义基础定义特殊规定关键字与标识符…...
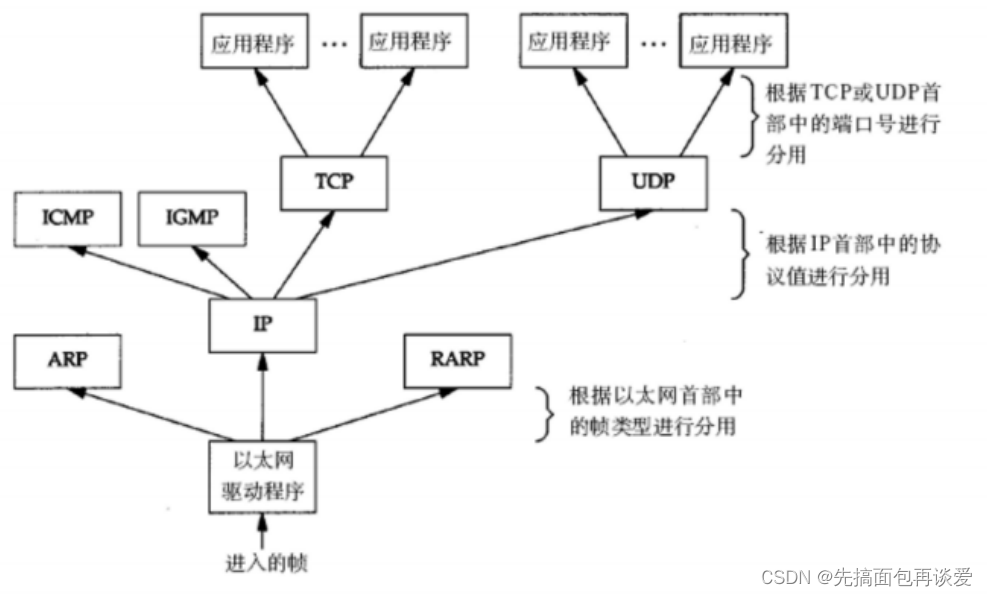
【网络】网络扫盲篇 ——用简单语言和图解带你入门网络
网络的一些名词和基础知识讲解 前言正式开始一些基础知识发展背景运营商和生产商 协议协议的分层TCP/IP五层(或四层)模型(可以不看,对新手来说太痛苦了,我这里只是为了让屏幕前的你过一遍就好,里面很多概念新手是不太懂的…...
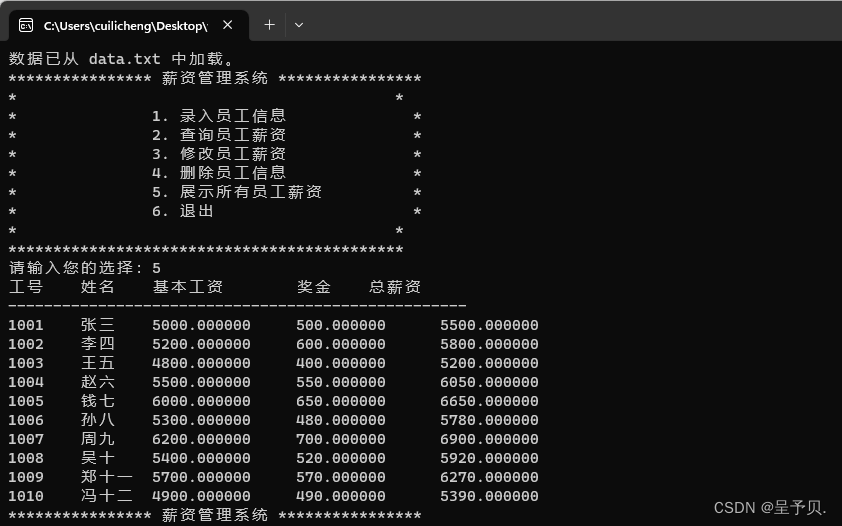
【项目开发 | C语言项目 | C语言薪资管理系统】
本项目是一个简单的薪资管理系统,旨在为用户提供方便的员工薪资管理功能,如添加、查询、修改、删除员工薪资信息等。系统通过命令行交互界面与用户进行交互,并使用 txt 文件存储员工数据。 一,开发环境需求 操作系统:w…...
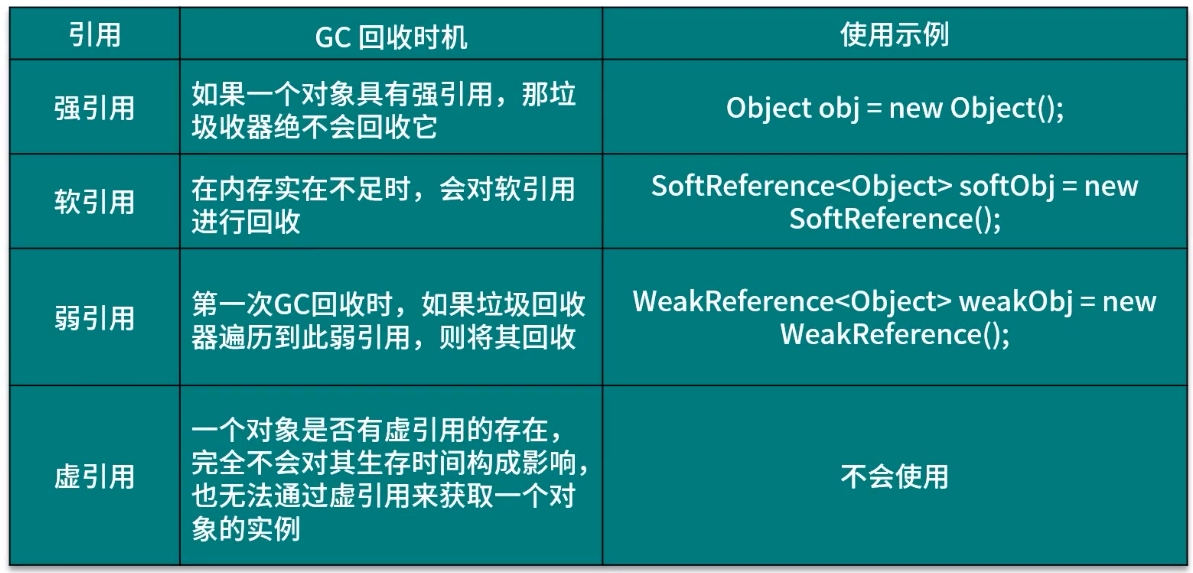
Android---GC回收机制与分代回收策略
目录 GC 回收机制 垃圾回收(Garbage Collection, GC) 垃圾回收算法 JVM 分代回收策略 1. 新生代 2. 老年代 GC Log 分析 引用 GC 回收机制 垃圾回收(Garbage Collection, GC) 垃圾就是内存中已经没有用的对象,JVM 中的垃圾回收器(Garbage Collector)会自…...
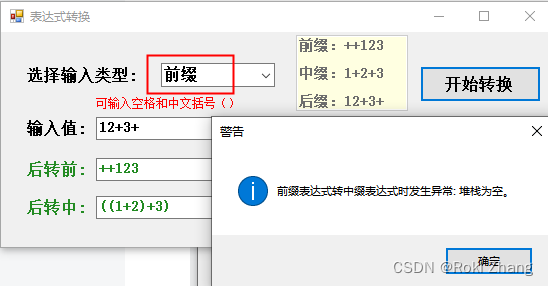
前缀、中缀、后缀表达式相互转换工具
目录 1. 界面一览 2. 使用说明 3. 实例演示 3.1 输入中缀 3.2 输入前缀 3.3 输入后缀 3.4 选择错误的类型 4. 代码 5. 资源地址 关于什么是前缀、中缀、后缀表达式,相信你不知道这个东西,那你也不会点进来这篇博客,当然,…...

Vue之ElementUI之动态树+数据表格+分页(项目功能)
目录 前言 一、实现动态树形菜单 1. 配置相应路径 2. 创建组件 3. 配置组件与路由的关系 index.js 4. 编写动态树形菜单 5. 页面效果演示 二、实现数据表格绑定及分页功能 1. 配置相应路径 2. 编写数据表格显示及分页功能代码 BookList.vue 3. 演示效果 总结 前言…...
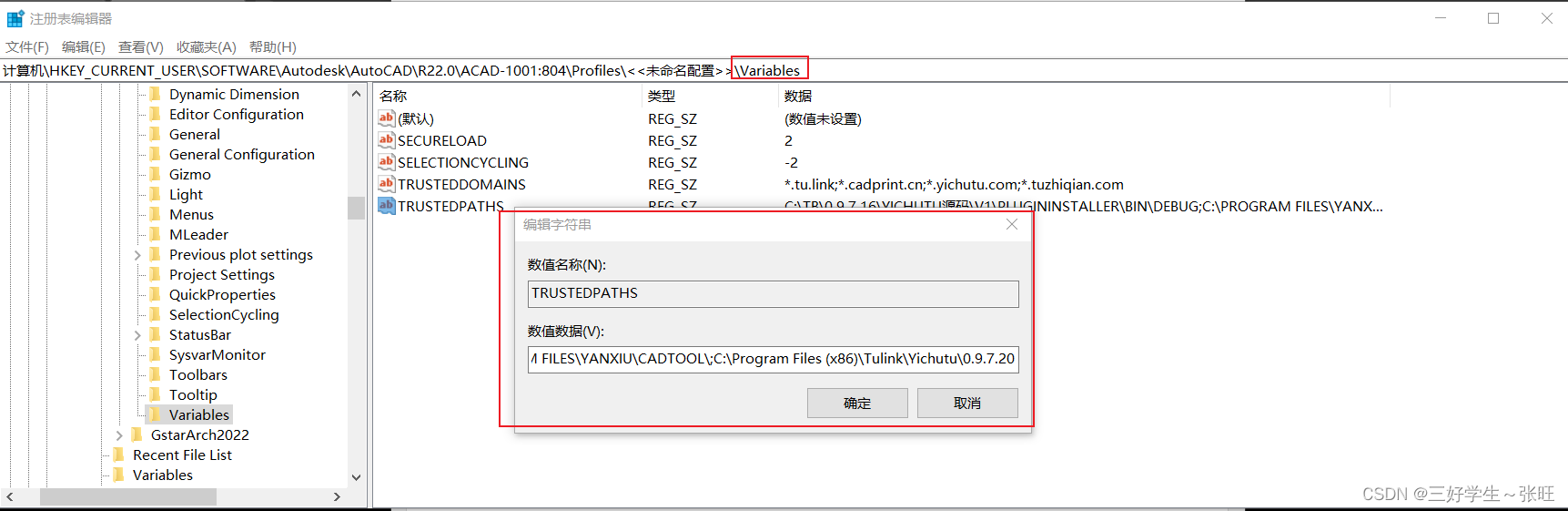
【CAD二次开发】给CAD添加TRUSTEDPATHS避免dll插件信任弹窗
找到配置文件目录,遍历下面的每个配置文件; 找到 Variables 下的TRUSTEDPATHS项目;在后面添加新的目录即可,多个目录使用分号分隔; public static void AddPath(string trusedPath){// 指定注册表键的路径...

编译和链接
编译和链接 一:???二:翻译环境1:编译1:预处理2:编译 2:链接 三:运行环境: 本文章所使用的图片均来在yyds鹏哥一:?…...
常识判断 --- 科技常识
目录 力与热 光和声 航空成就 垃圾分类 百科知识 血型 二十四节气歌 春雨惊春清谷天 夏满忙夏暑相连 秋处露秋寒霜降 冬雪雪冬小大寒 力与热 光和声 航空成就 垃圾分类 百科知识 血型...
修改npm全局安装的插件(下载目录指向)
我们先打开终端 然后执行 npm config get prefix查看npm 的下载地址 一般都会在C盘 但是 我们都知道 C盘下东西多了是很不好的 所以 我们可以执行 npm config set prefix “E:\npmfile”将 npm 的下载地址 改变成 E盘下的 npmfile目录 这样 以后 默认全局安装的插件就会都到…...
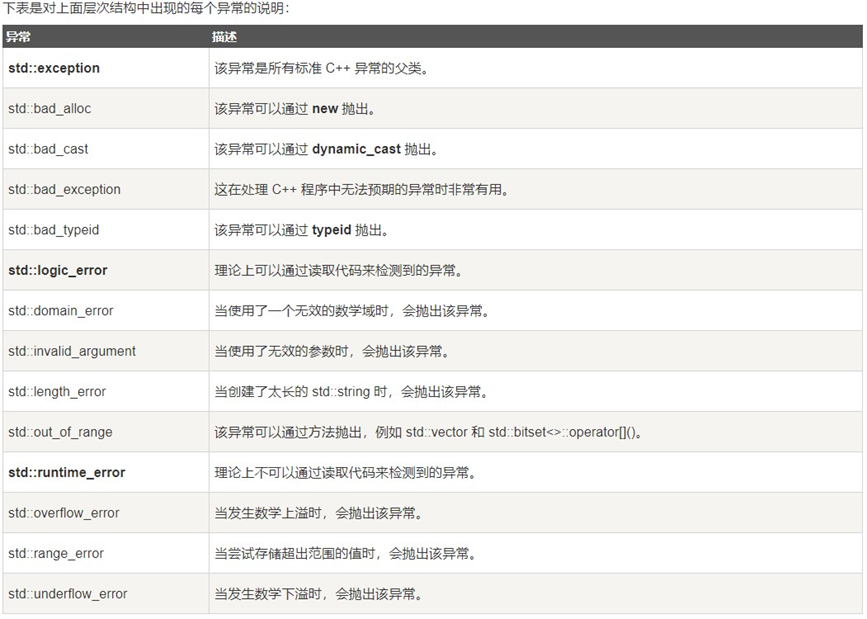
<C++> 异常
C语言传统的处理错误的方式 传统的错误处理机制: 终止程序,如assert,缺陷:用户难以接受。如发生内存错误,除0错误时就会终止程序。返回错误码,缺陷:需要程序员自己去查找对应的错误。如系统的…...

聊聊HttpClientBuilder
序 本文主要研究一下HttpClientBuilder HttpClientBuilder httpclient-4.5.10-sources.jar!/org/apache/http/impl/client/HttpClientBuilder.java public class HttpClientBuilder {public static HttpClientBuilder create() {return new HttpClientBuilder();}protected…...
MacOS - Sonoma更新了啥
1 系统介绍 苹果公司于2023年9月26日发布了macOS Sonoma 14.0正式版。名称由来不知道,可能是地名:Sonoma是一个地名,指加利福尼亚州北部索诺玛县(Sonoma County)。 2 系统重要更新 2.1 将小组件添加到桌面 速览提醒事项和临近日程等。按住Control键点…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
