【算法|动态规划No.7】leetcode300. 最长递增子序列
个人主页:兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
点击直接跳转到该题目
1️⃣题目描述
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
注意:
- 1 <= nums.length <= 2500
- -10^4 <= nums[i] <= 10^4
2️⃣题目解析
本题目使用动态规划来解决此问题。
dp[i]表示以第i个元素结尾的最长递增子序列的长度。通过不断更新以每个元素结尾的最长递增子序列的长度,最终得到整个数组的最长递增子序列的长度。
对于每个位置i,都需要遍历位置i之前的所有元素(j=0到i-1),判断当前元素nums[i]和之前的元素nums[j]的大小关系。
如果nums[i]大于nums[j],说明当前元素可以接在nums[j]构成的递增子序列后面,更新dp[i]为dp[j]+1,表示将当前元素纳入递增子序列中的长度。
3️⃣解题代码
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n,1);int ret = 1;for(int i =1;i < n;i++){for(int j =0;j < i;j++)if(nums[i] > nums[j])dp[i] = max(dp[j]+1,dp[i]);ret = max(ret,dp[i]);}return ret;}
};
最后就是代码通过啦!!!
相关文章:

【算法|动态规划No.7】leetcode300. 最长递增子序列
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

LeetCode 54 螺旋矩阵
先贴代码 class Solution {public int[][] generateMatrix(int n) {int left 0;int right n-1;int up 0;int down n-1;int[][] result new int[n][n];int number 0;while(left < right && up < down) {for(int ileft;i<right;i) {number;result[up]…...

OpenCV 概念、整体架构、各模块主要功能
文章目录 1. OpenCV 概念2 OpenCV主要模块3 各模块 详细介绍3.1 calib3d 标定3.2 core 核心功能模块3.4 features2d 二维特征3.5 flann 快速近似近邻算法库3.7 highgui 高级图形用户界面3.9 imgproc 图像处理模块3.10 ml 机器学习模块3.11 objdetect 目标检测模块3.12 photo 数…...

组合数与莫队——组合数前缀和
用莫队求组合数是一种常见套路 莫队求 S ( n , m ) ∑ i 0 m ( n i ) S(n,m)\sum_{i0}^m\binom n i S(n,m)∑i0m(in) S ( n , m 1 ) S(n,m1) S(n,m1) 直接做个差,然后就相当于加上 ( n i 1 ) \binom n {i1} (i1n) 求 S ( n 1 , m ) S(n1,m) S(n1,m)…...
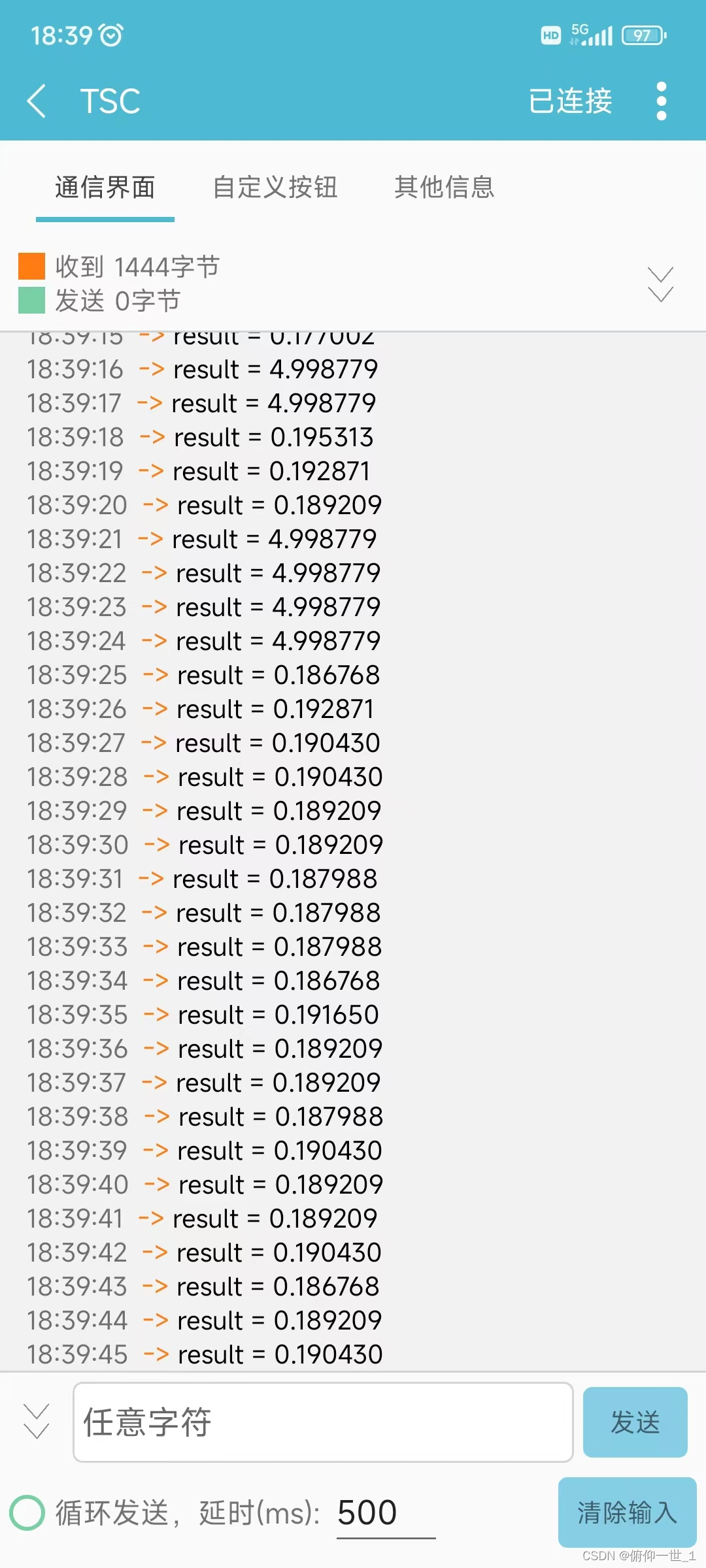
stm32之雨滴传感器使用记录
一、简介 雨滴传感器、烟雾传感器(MQ2)、轨迹传感器、干黄管等的原理都类似,都是将检测到的信号通过LM393进行处理之后再输出,可以输出数字信号DO(0和1)和模拟信号A0。 雨滴传感器在正常情况下是AO输出的是…...
华硕平板k013me176cx线刷方法
1.下载adb刷机工具, 或者刷机精灵 2.下载刷机rom包 华硕asus k013 me176cx rom固件刷机包-CSDN博客 3.平板进入刷机界面 进入方法参考: ASUS (k013) ME176CX不进入系统恢复出厂设置的方法-CSDN博客 4.解压ME176C-CN-3_2_23_182.zip,把UL-K013-CN-3.2.…...
C#停车场管理系统
目录 一、绪论1.1内容简介及意义1.2开发工具及技术介绍 二、总体设计2.1系统总体架构2.2登录模块总体设计2.3主界面模块总体设计2.4停车证管理模块总体设计2.5停车位管理模块总体设计2.6员工管理模块总体设计2.7其他模块总体设计 三、详细设计3.1登录模块设计3.2主界面模块设计…...
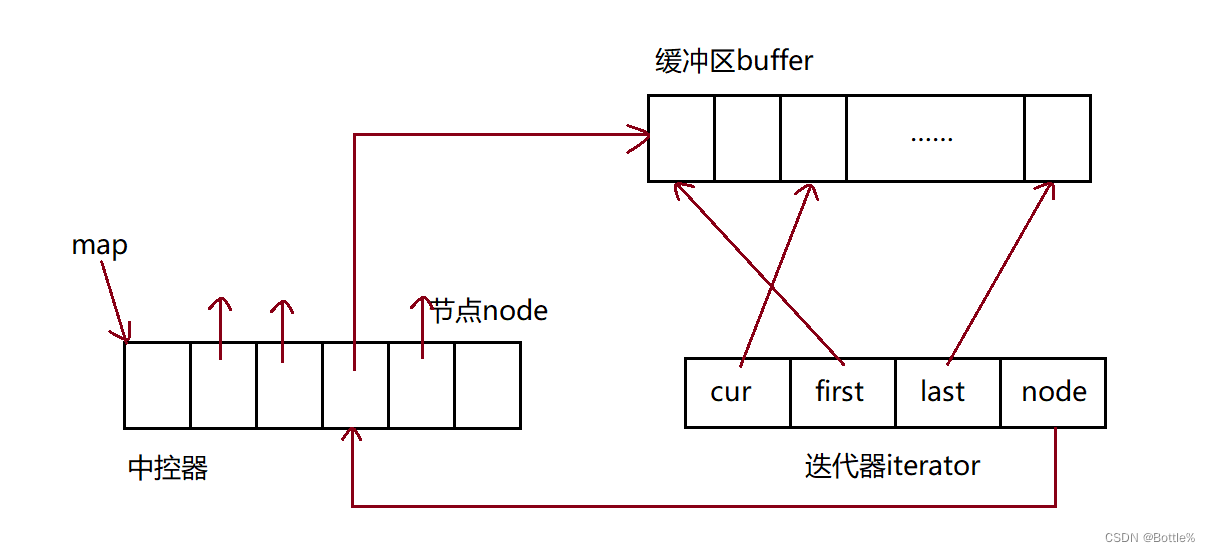
C++:stl:stack、queue、priority_queue介绍及模拟实现和容量适配器deque介绍
本文主要介绍c中stl的栈、队列和优先级队列并对其模拟实现,对deque进行一定介绍并在栈和队列的模拟实现中使用。 目录 一、stack的介绍和使用 1.stack的介绍 2.stack的使用 3.stack的模拟实现 二、queue的介绍和使用 1.queue的介绍 2.queue的使用 3.queue的…...

【Java】面向对象程序设计 课程笔记 面向对象基础
🚀Write In Front🚀 📝个人主页:令夏二十三 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:Java 💬总结:希望你看完之后,能对你有…...
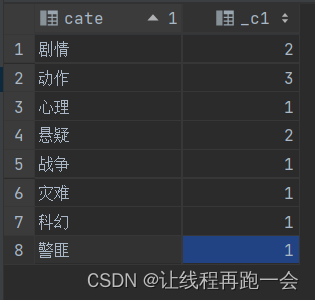
Hive【Hive(五)函数-高级聚合函数、炸裂函数】
高级聚合函数 多进一出(多行输入,一个输出) 普通聚合函数:count、sum ... 1)collect_list():收集并形成 list 集合,结果不去重 select sex,collect_list(job) from e…...
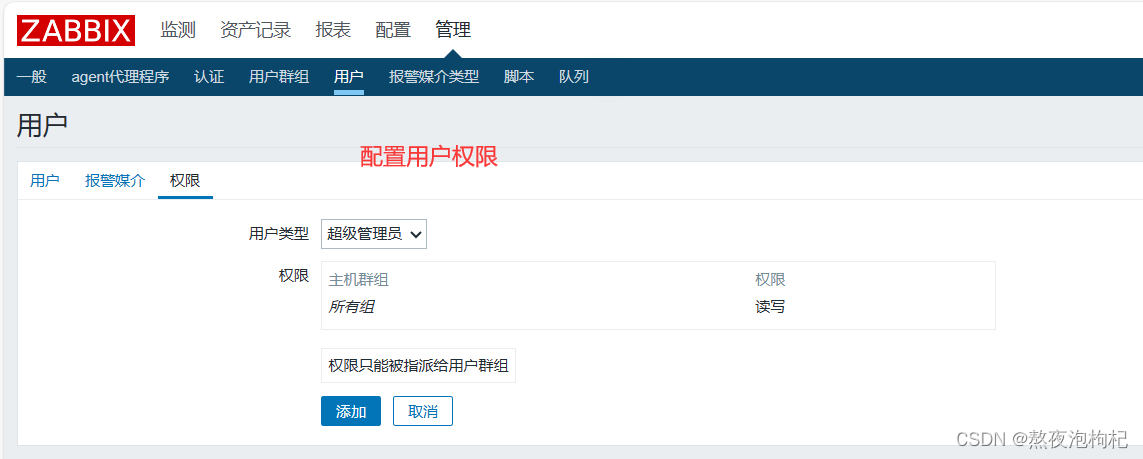
zabbix(二)
文章目录 1. zabbix自定义监控项【配置】2. zabbix自定义监控项【传参】3. zabbix自定义触发器4. zabbix邮件告警4. zabbix企业微信告警 1. zabbix自定义监控项【配置】 目前有主机zabbix-server: 10.0.0.10 zabbix-slave: 10.0.0.11 zabbix监控的内容,想平滑转移到…...

容器安全检测工具KubeHound使用
前言 Kubernetes集群攻击路径AES工具 安装 下载kubehound git clone https://github.com/DataDog/KubeHound.git 安装docker compose插件 Docker compose插件安装_信安成长日记的博客-CSDN博客 启动kubehound后端服务 即要开大内存,不然db起不来,…...
机器学习笔记 - 基于强化学习的贪吃蛇玩游戏
一、关于深度强化学习 如果不了解深度强化学习的一般流程的可以考虑看一下下面的链接。因为这里的示例因为在PyTorch 之上实现深度强化学习算法。 机器学习笔记 - Deep Q-Learning算法概览深度Q学习是一种强化学习算法,它使用深度神经网络来逼近Q函数,用于确定在给定状态下采…...

C++_pen_类
类的成员函数 构造函数析构函数普通成员函数 构造函数与析构函数 #include <stdio.h> class STU{ public:STU(){printf("STU\n");}STU(int id){printf("STU(int id)\n");}~STU(){printf("STU Bye!!!\n");} };int main(int argc, char c…...

MySQL 多表关联查询优化实践和原理解析
目录 一、前言二、表数据准备三、表关联查询原理和两种算法3.1、研究关联查询算法必备知识点3.2、嵌套循环连接 Nested-Loop Join(NLJ) 算法3.3、基于块的嵌套循环连接 Block Nested-Loop Join(BNL)算法3.4、被驱动表的关联字段没索引为什么要选择使用 BNL 算法而不使用 Nested…...
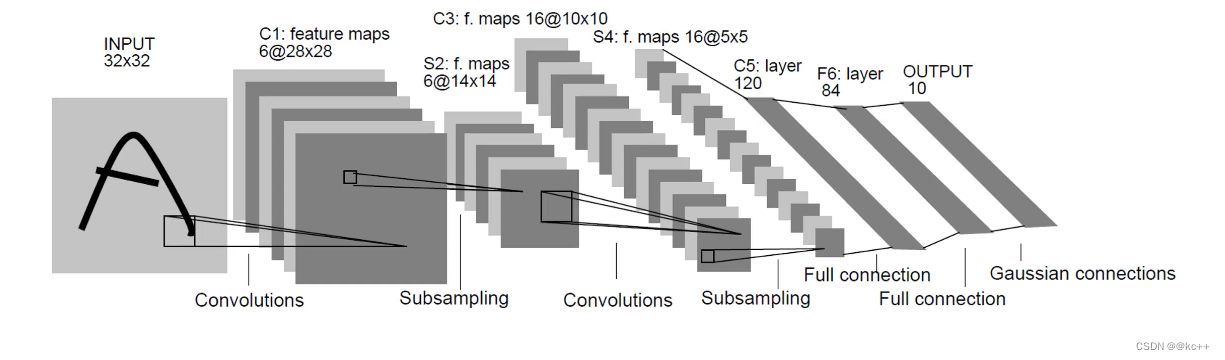
LeNet网络复现
文章目录 1. LeNet历史背景1.1 早期神经网络的挑战1.2 LeNet的诞生背景 2. LeNet详细结构2.1 总览2.2 卷积层与其特点2.3 子采样层(池化层)2.4 全连接层2.5 输出层及激活函数 3. LeNet实战复现3.1 模型搭建model.py3.2 训练模型train.py3.3 测试模型test…...

Oracle 慢查询排查步骤
目录 1. Oracle 慢查询排查步骤1.1. 前言1.2. 排查步骤1.2.1. 查询慢查询日志1.2.2. Oracle 查询 SQL 语句执行的耗时1.2.3. 定位系统里面哪些 SQL 脚本存在 TABLE ACCESS FULL (扫全表) 行为1.2.4. 查看索引情况1.2.5. 查看锁的竞争情况1.2.6. 其他锁语句 1.3. 慢查询优化1.3.…...

互联网Java工程师面试题·MyBatis 篇·第二弹
目录 16、Xml 映射文件中,除了常见的 select|insert|updae|delete标签之外,还有哪些标签? 17、Mybatis 的 Xml 映射文件中,不同的 Xml 映射文件,id 是否可以重复? 18、为什么说 Mybatis 是半自动 ORM 映射…...
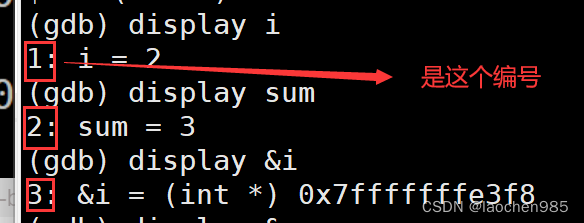
Linux 下如何调试代码
debug 和 release 在Linux下的默认模式是什么? 是release模式 那你怎么证明他就是release版本? 我们知道如果一个程序可以被调试,那么它一定是debug版本,如果它是release版本,它是没法被调试的,所以说我们可以来调试一…...
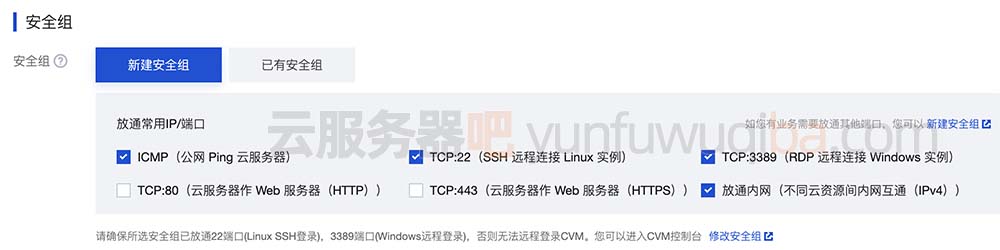
腾讯云服务器简介和使用流程
腾讯云服务器在云服务器CVM或轻量应用服务器页面自定义购买价格比较贵,但是自定义购买云服务器CPU内存带宽配置选择范围广,活动上购买只能选择固定的活动机,选择范围窄,但是云服务器价格便宜比较省钱。腾讯云服务器网来详细说下腾…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

