力扣 -- 518. 零钱兑换 II(完全背包问题)

解题步骤:



参考代码:
未优化代码:
class Solution {
public:int change(int amount, vector<int>& coins) {int n=coins.size();//多开一行,多开一列vector<vector<int>> dp(n+1,vector<int>(amount+1));//初始化dp[0][0]=1,其它的dp[0][j]都为0,因为不存在,所以只有0种选法dp[0][0]=1;//不要把dp[0][j]剩下的值初始化成-1,曾经因初始化成-1而出错//第一列不需要初始化//填表for(int i=1;i<=n;i++){//记得从0开始for(int j=0;j<=amount;j++){dp[i][j]=dp[i-1][j];if(j>=coins[i-1]&&dp[i][j-coins[i-1]]!=0){dp[i][j]+=dp[i][j-coins[i-1]];}}}//返回值return dp[n][amount];}
};优化后代码:
class Solution {
public:int change(int amount, vector<int>& coins) {int n=coins.size();vector<int> dp(amount+1);//初始化dp[0]=1;//填表for(int i=1;i<=n;i++){for(int j=coins[i-1];j<=amount;j++){if(dp[j-coins[i-1]]!=0){dp[j]+=dp[j-coins[i-1]];}}}//返回值return dp[amount];}
};你学会了吗???
相关文章:

力扣 -- 518. 零钱兑换 II(完全背包问题)
解题步骤: 参考代码: 未优化代码: class Solution { public:int change(int amount, vector<int>& coins) {int ncoins.size();//多开一行,多开一列vector<vector<int>> dp(n1,vector<int>(amount1…...
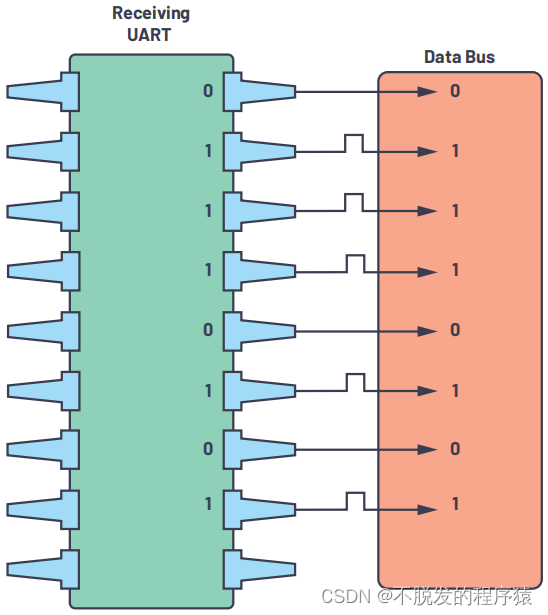
一文搞懂UART通信协议
目录 1、UART简介 2、UART特性 3、UART协议帧 3.1、起始位 3.2、数据位 3.3、奇偶校验位 3.4、停止位 4、UART通信步骤 1、UART简介 UART(Universal Asynchronous Receiver/Transmitter,通用异步收发器)是一种双向、串行、异步的通信…...
【算法|动态规划No.7】leetcode300. 最长递增子序列
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

LeetCode 54 螺旋矩阵
先贴代码 class Solution {public int[][] generateMatrix(int n) {int left 0;int right n-1;int up 0;int down n-1;int[][] result new int[n][n];int number 0;while(left < right && up < down) {for(int ileft;i<right;i) {number;result[up]…...

OpenCV 概念、整体架构、各模块主要功能
文章目录 1. OpenCV 概念2 OpenCV主要模块3 各模块 详细介绍3.1 calib3d 标定3.2 core 核心功能模块3.4 features2d 二维特征3.5 flann 快速近似近邻算法库3.7 highgui 高级图形用户界面3.9 imgproc 图像处理模块3.10 ml 机器学习模块3.11 objdetect 目标检测模块3.12 photo 数…...

组合数与莫队——组合数前缀和
用莫队求组合数是一种常见套路 莫队求 S ( n , m ) ∑ i 0 m ( n i ) S(n,m)\sum_{i0}^m\binom n i S(n,m)∑i0m(in) S ( n , m 1 ) S(n,m1) S(n,m1) 直接做个差,然后就相当于加上 ( n i 1 ) \binom n {i1} (i1n) 求 S ( n 1 , m ) S(n1,m) S(n1,m)…...
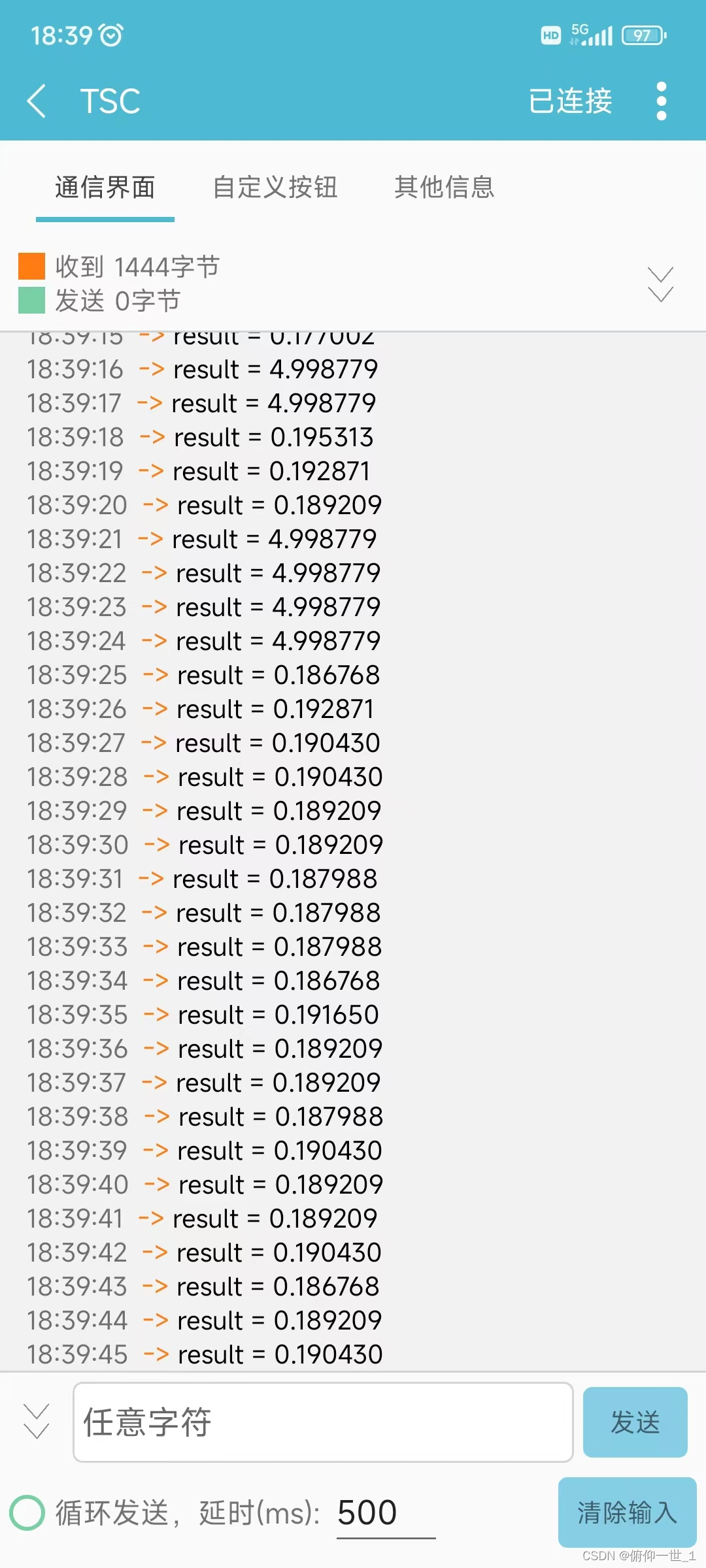
stm32之雨滴传感器使用记录
一、简介 雨滴传感器、烟雾传感器(MQ2)、轨迹传感器、干黄管等的原理都类似,都是将检测到的信号通过LM393进行处理之后再输出,可以输出数字信号DO(0和1)和模拟信号A0。 雨滴传感器在正常情况下是AO输出的是…...
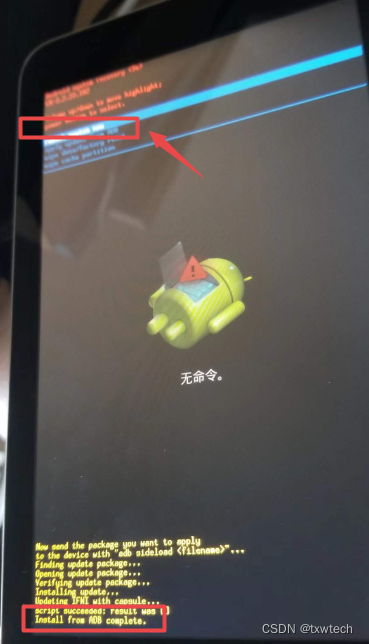
华硕平板k013me176cx线刷方法
1.下载adb刷机工具, 或者刷机精灵 2.下载刷机rom包 华硕asus k013 me176cx rom固件刷机包-CSDN博客 3.平板进入刷机界面 进入方法参考: ASUS (k013) ME176CX不进入系统恢复出厂设置的方法-CSDN博客 4.解压ME176C-CN-3_2_23_182.zip,把UL-K013-CN-3.2.…...
C#停车场管理系统
目录 一、绪论1.1内容简介及意义1.2开发工具及技术介绍 二、总体设计2.1系统总体架构2.2登录模块总体设计2.3主界面模块总体设计2.4停车证管理模块总体设计2.5停车位管理模块总体设计2.6员工管理模块总体设计2.7其他模块总体设计 三、详细设计3.1登录模块设计3.2主界面模块设计…...
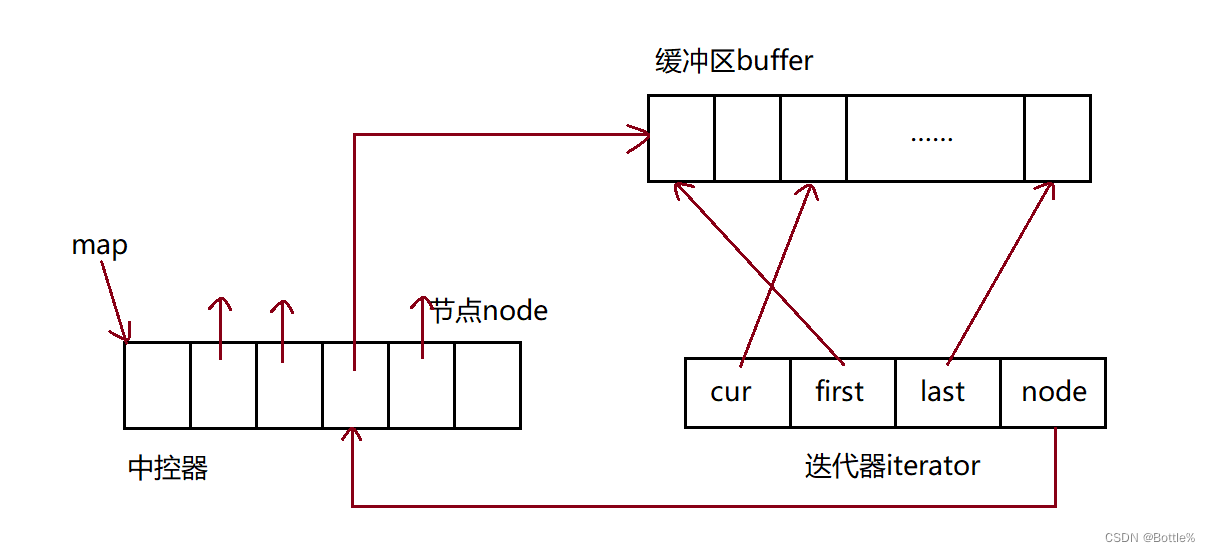
C++:stl:stack、queue、priority_queue介绍及模拟实现和容量适配器deque介绍
本文主要介绍c中stl的栈、队列和优先级队列并对其模拟实现,对deque进行一定介绍并在栈和队列的模拟实现中使用。 目录 一、stack的介绍和使用 1.stack的介绍 2.stack的使用 3.stack的模拟实现 二、queue的介绍和使用 1.queue的介绍 2.queue的使用 3.queue的…...

【Java】面向对象程序设计 课程笔记 面向对象基础
🚀Write In Front🚀 📝个人主页:令夏二十三 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:Java 💬总结:希望你看完之后,能对你有…...
Hive【Hive(五)函数-高级聚合函数、炸裂函数】
高级聚合函数 多进一出(多行输入,一个输出) 普通聚合函数:count、sum ... 1)collect_list():收集并形成 list 集合,结果不去重 select sex,collect_list(job) from e…...
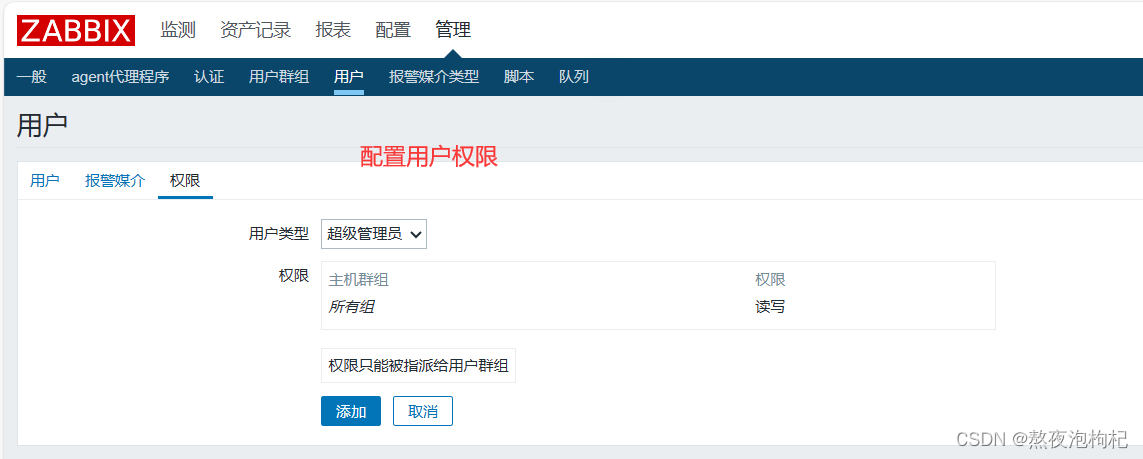
zabbix(二)
文章目录 1. zabbix自定义监控项【配置】2. zabbix自定义监控项【传参】3. zabbix自定义触发器4. zabbix邮件告警4. zabbix企业微信告警 1. zabbix自定义监控项【配置】 目前有主机zabbix-server: 10.0.0.10 zabbix-slave: 10.0.0.11 zabbix监控的内容,想平滑转移到…...

容器安全检测工具KubeHound使用
前言 Kubernetes集群攻击路径AES工具 安装 下载kubehound git clone https://github.com/DataDog/KubeHound.git 安装docker compose插件 Docker compose插件安装_信安成长日记的博客-CSDN博客 启动kubehound后端服务 即要开大内存,不然db起不来,…...
机器学习笔记 - 基于强化学习的贪吃蛇玩游戏
一、关于深度强化学习 如果不了解深度强化学习的一般流程的可以考虑看一下下面的链接。因为这里的示例因为在PyTorch 之上实现深度强化学习算法。 机器学习笔记 - Deep Q-Learning算法概览深度Q学习是一种强化学习算法,它使用深度神经网络来逼近Q函数,用于确定在给定状态下采…...

C++_pen_类
类的成员函数 构造函数析构函数普通成员函数 构造函数与析构函数 #include <stdio.h> class STU{ public:STU(){printf("STU\n");}STU(int id){printf("STU(int id)\n");}~STU(){printf("STU Bye!!!\n");} };int main(int argc, char c…...

MySQL 多表关联查询优化实践和原理解析
目录 一、前言二、表数据准备三、表关联查询原理和两种算法3.1、研究关联查询算法必备知识点3.2、嵌套循环连接 Nested-Loop Join(NLJ) 算法3.3、基于块的嵌套循环连接 Block Nested-Loop Join(BNL)算法3.4、被驱动表的关联字段没索引为什么要选择使用 BNL 算法而不使用 Nested…...
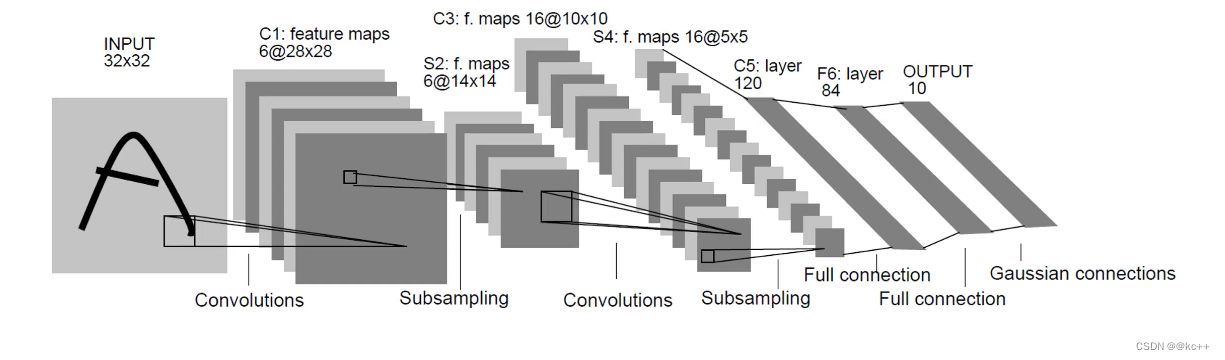
LeNet网络复现
文章目录 1. LeNet历史背景1.1 早期神经网络的挑战1.2 LeNet的诞生背景 2. LeNet详细结构2.1 总览2.2 卷积层与其特点2.3 子采样层(池化层)2.4 全连接层2.5 输出层及激活函数 3. LeNet实战复现3.1 模型搭建model.py3.2 训练模型train.py3.3 测试模型test…...

Oracle 慢查询排查步骤
目录 1. Oracle 慢查询排查步骤1.1. 前言1.2. 排查步骤1.2.1. 查询慢查询日志1.2.2. Oracle 查询 SQL 语句执行的耗时1.2.3. 定位系统里面哪些 SQL 脚本存在 TABLE ACCESS FULL (扫全表) 行为1.2.4. 查看索引情况1.2.5. 查看锁的竞争情况1.2.6. 其他锁语句 1.3. 慢查询优化1.3.…...

互联网Java工程师面试题·MyBatis 篇·第二弹
目录 16、Xml 映射文件中,除了常见的 select|insert|updae|delete标签之外,还有哪些标签? 17、Mybatis 的 Xml 映射文件中,不同的 Xml 映射文件,id 是否可以重复? 18、为什么说 Mybatis 是半自动 ORM 映射…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
