10.3作业
#include <myhead.h>
int main(int argc, const char *argv[])
{
mkfifo(“./f1”,0777);
mkfifo(“./f2”,0777);
pid_t cpid = fork();
if(0 < cpid)
{
int fdw = open(“./f1”,O_WRONLY);
int fdr = open(“./f2”,O_RDONLY);
char buf[128] = “”;
while(1)
{
bzero(buf,sizeof(buf));
printf(“父进程请输入>>>>>\n”);
scanf(“%s”,buf);
write(fdw,buf,sizeof(buf));
bzero(buf,sizeof(buf));
read(fdr,buf,sizeof(buf));
printf(“父进程接收打印:%s\n”,buf);
}close(fdw);close(fdr);
}
if(0 == cpid)
{int fdr = open("./f1",O_RDONLY);int fdw = open("./f2",O_WRONLY);char buf[128] = "";while(1){ bzero(buf,sizeof(buf));read(fdr,buf,sizeof(buf));printf("子进程接收打印:%s\n",buf);bzero(buf,sizeof(buf));printf("子进程请输入>>>>>\n");scanf("%s",buf);write(fdw,buf,sizeof(buf));}close(fdw);close(fdr);
}
return 0;
}
相关文章:

10.3作业
#include <myhead.h> int main(int argc, const char *argv[]) { mkfifo(“./f1”,0777); mkfifo(“./f2”,0777); pid_t cpid fork(); if(0 < cpid) { int fdw open(“./f1”,O_WRONLY); int fdr open(“./f2”,O_RDONLY); char buf[128] “”; while(1) { bzero…...

Springboot中的@Import注解~
Import注解是Spring框架中的注解之一,用于导入其他配置类或者组件 Import注解的作用有以下几点: 导入其他配置类:可以使用Import注解导入其他的配置类,将其加入到当前配置类中,从而可以共享配置信息 导入其他组件&am…...
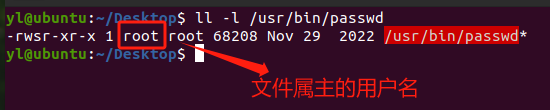
Linux 安全 - SUID机制
文章目录 一、文件权限位二、SUID简介 一、文件权限位 (1) $ ls -l text.txt -rw-rw-r-- 1 yl yl 0 Sep 28 16:25 text.txt其中第一个字段-rw-rw-r–,我们可以把它分为四部分看: -rw-rw-r--(1)- &a…...
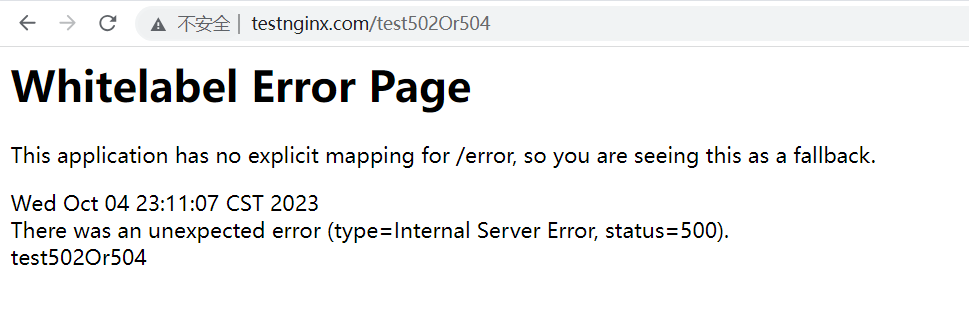
Nginx与Spring Boot的错误模拟实践:探索502和504错误的原因
文章目录 前言502和504区别---都是Nginx返回的access.log和error.log介绍SpringBoot结合Nginx实战502 and 504准备工作Nginx配置host配置SpringBoot 502模拟access.logerror.log 504模拟access.logerror.log 500模拟access.logerror.log 总结 前言 刚工作那会,最常…...
全志ARM926 Melis2.0系统的开发指引①
全志ARM926 Melis2.0系统的开发指引① 1. 编写目的2. Melis2.0 系统概述3. Melis2.0 快速开发3.1. Melis2.0 SDK 目录结构3.2. Melis2.0 编译环境3.3. Melis2.0 固件打包3.4. Melis2.0 固件烧录3.5.串口打印信息3.6. Melis2.0 添加和调用一个模块3.6.1. 为什么划分模块…...
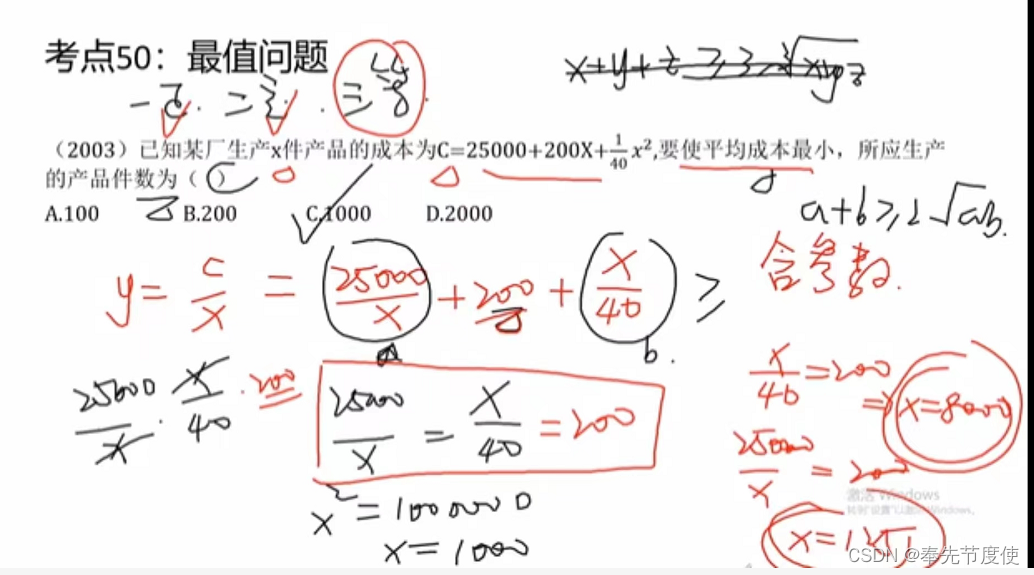
2024级199管理类联考之数学基础(下篇)
平面几何(平均2题) 三角形(性质、特殊三角形、全等与相似) 性质 由不在同一直线的三条线段首尾依次连接所组成的图形三条边、三个内角、三个定点三角形内角和为180度,外角和为360度,多边形的外角和为360度,n多边形的内角和为(n-2)*180度一个外角等于不相邻的两个内角之和任意…...

HTML之如何下载网页中的音频(二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...
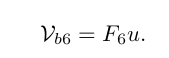
【现代机器人学】学习笔记十四:中文版印刷/翻译勘误
首先声明,这个印刷/勘误并非经过官方的认可,只是我个人的粗浅的理解。如果内容有误,恳请大家谅解指正。 其实有的并不算错,只是我个人认为不太准确,在我学习过程中产生了一些小疑惑和误解。 都是一些小毛病ÿ…...
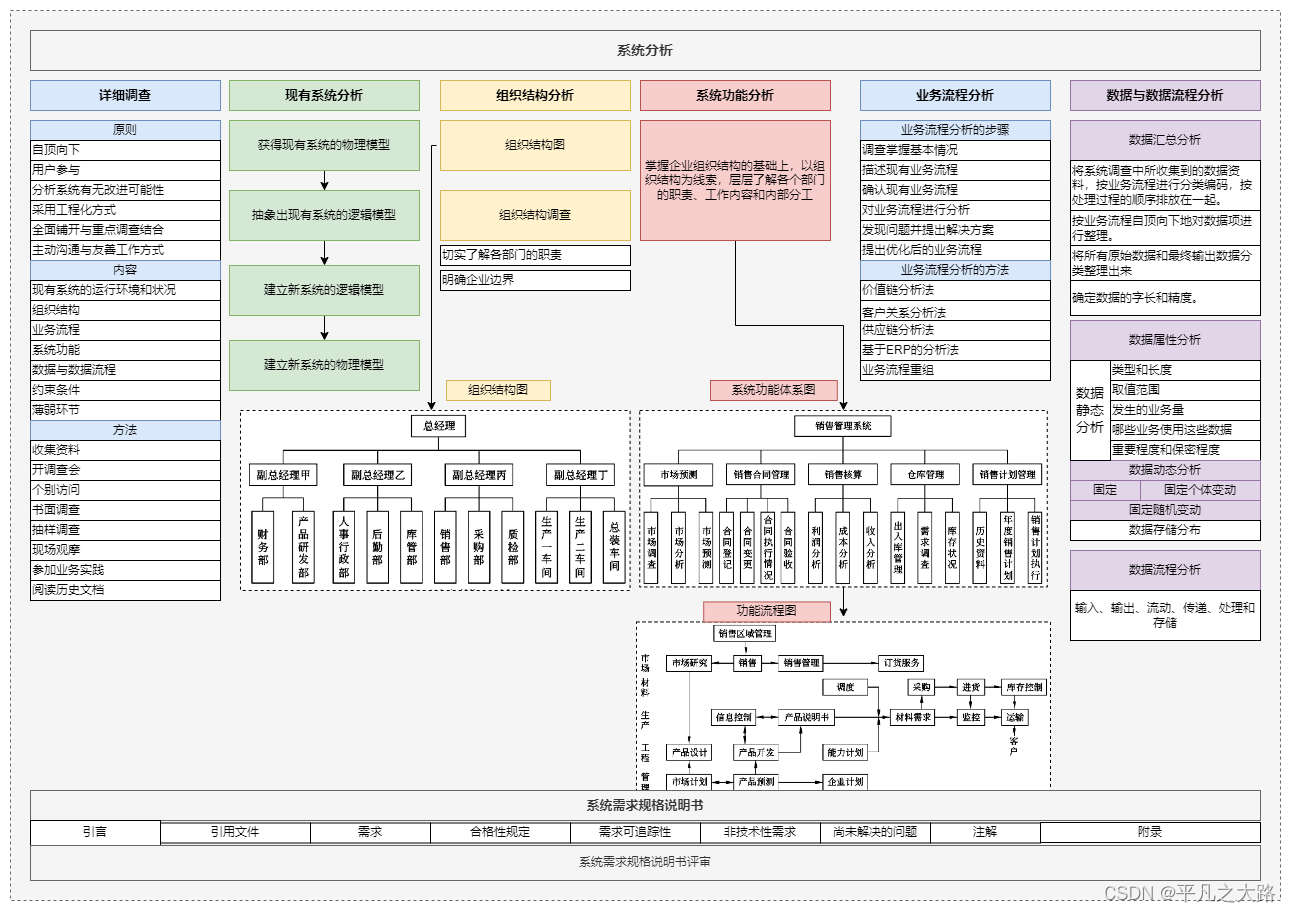
[架构之路-229]:计算机体硬件与系结构 - 计算机系统的矩阵知识体系结构
目录 一、纵向:目标系统的分层结构 1.1 目标系统的架构 1.2 网络协议栈 1.3 计算机程序语言分层 二、横向(构建目标系统的时间、开发阶段):软件工程 三、二维矩阵知识体系结构 一、纵向:目标系统的分层结构 1.1…...
第一章 visual studio下载安装
一、官网下载 地址:https://visualstudio.microsoft.com/zh-hans/ 点击免费visual studio 二、安装 运行下载好的exe文件,自定义安装目录 三、选择需要的组件安装 只需要选择标记组件,然后点击安装 等待安装完成就行 四、重启电脑 安装完之后…...

【服务器】在 Linux CLI 下安装 Anaconda
【服务器】在 Linux CLI 下安装 Anaconda 1 系统环境2 下载安装包3 安装 1 系统环境 查看系统信息 cat /etc/os-release2. 查看架构 uname -a # output # Linux localhost.localdomain 4.18.0-193.28.1.el8_2.x86_64 #1 SMP Thu Oct 22 00:20:22 UTC 2020 x86_64 x86_64 x86…...

Python中Lambda用法
在Python中,lambda函数是一种形式较短的函数,又称为匿名函数。与正常的函数不同,lambda函数没有名称,因此只能在定义时直接传递给其他函数或变量使用,而不能单独调用。 lambda函数的语法非常简单,格式如下…...
nodejs+vue养老人员活体鉴权服务系统elementui
系统 统计数据:统计报表、人员台账、机构数据、上报数据、核验报表等,养老人员活体鉴权服务是目前国家养老人员管理的重要环节,主要为以养老机构中养老人员信息为基础,每月进行活体鉴权识别并统计数据为养老补助等管理。前端功能&…...
)
解决caffe中的python环境安装的问题(补充)
上一篇(解决caffe中的python环境安装的问题_qiuchangyong的博客-CSDN博客)说到了安装过程中遇到的常见问题,其实还有一个忘了补充,就是在执行命令"sudo python -m pip install -r requirements.txt"后,出现p…...

面试常用排序查找算法
文章目录 1 二分查找2 冒泡排序3 堆排序4 插入排序5 快速排序6 选择排序7 希尔排序 1 二分查找 定义两个变量left和right,分别表示数组的左边界和右边界,初始值分别为0和len - 1,其中len是数组的长度。计算数组的中间位置mid,公式…...

CUDA C编程权威指南:1.1-CUDA基础知识点梳理
主要整理了N多年前(2013年)学习CUDA的时候开始总结的知识点,好长时间不写CUDA代码了,现在LLM推理需要重新学习CUDA编程,看来出来混迟早要还的。 1.CUDA 解析:2007年,NVIDIA推出CUDA(…...

讲讲项目里的仪表盘编辑器(四)分页卡和布局容器组件
讲讲两个经典布局组件的实现 ① 布局容器组件 配置面板是给用户配置布局容器背景颜色等属性。这里我们不需要关注 定义文件 规定了组件类的类型、标签、图标、默认布局属性、主文件等等。 // index.js import Container from ./container.vue; class ContainerControl extends…...

Qt模块、Qt开发应用程序类型、Qt未来主要市场、Qt6功能普及
Qt模块、Qt开发应用程序类型、Qt未来主要市场、Qt6功能普及 文章目录 1.Qt核心模块2.Qt的功能拓展3.Qt未来主要市场4.Qt6功能普及5.弃用的功能: Qt是一个跨平台的应用程序开发框架,提供了丰富的模块和工具来开发各种类型的应用程序。以下是Qt目前已有的…...

nodejs+vue高校校图书馆elementui
管理员输入书籍所在的书架位置,借阅提醒系统:可以查看个人借阅信息和图书到期提醒、挂失、检索、虚拟借书证不仅为群众提供了服务,而且也推广了自己,让更多的群众了解自己。 管理员页面: 第三章 系统分析 10 3.1需求分…...

CUDA C编程权威指南:1.2-CUDA基础知识点梳理
主要整理了N多年前(2013年)学习CUDA的时候开始总结的知识点,好长时间不写CUDA代码了,现在LLM推理需要重新学习CUDA编程,看来出来混迟早要还的。 1.闭扫描和开扫描 对于一个二元运算符 ⊕ \oplus ⊕和一个 n n n元…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
