R语言易错点(持续更新中~~)
1.R向量元素的索引(下标)是从1开始的,而非0
>x
[1] 1 2 4>x[3]
[1] 42.[]和[ [ ] ]
mylist<-list(stud.id=1234,
+ stud.name="Tom",
+ stud.marks=c(10,3,14,25,19))
> mylist
$stud.id
[1] 1234$stud.name
[1] "Tom"$stud.marks
[1] 10 3 14 25 19mylist[[1]]
#输出
[1] 1234
mylist[1]
#输出
$stud.id
[1]1234mode(mylist[[1]])
#输出
[1] "numeric"mode(mylist[1])
#输出
[1] "list"mylist[[1]]
列表的第一个组件的值
类型为”numeric“
mylist[1]
第一个成分的子列表
类型为“list”
3.标量和一元向量
标量是只包含一个单一数值的数据类型,而长度为一的向量是包含一个元素的向量。
# 标量
x <- 5# 长度为一的向量
y <- c(5)通常情况下,标量可以被看作一元向量# 标量
x <- 5# 长度为一的向量
y <- c(5)# 进行乘法运算
result1 <- x * x
result2 <- y * y# 输出结果
print(result1)
print(result2)[1] 25
[1] 25#注意:使用向量化的运算符会使得函数也向量化
#这也适用于很多内置函数,例如round()
> y<-c(1.2,3.9,0.4)
> z<-round(y)
> z
[1] 1 4 0
#round()函数能应用到向量y的每一个元素中,标量实际上就是一元向量,所以对单个数值使用round()函数,只是一种特殊情况
round(1.2)
[1] 1#诸如+这样的运算符实际也是函数
> y<-c(12,5,13)
> y+4
[1] 16 9 17
这样写更加明显> '+'(y+4)
[1] 16 9 17
#在这里我们定义f(),我们希望c是标量,但实际上,他是一个长度为1的向量
#即使我们调用f()时给c指定的是单个数值,在f()计算x+c时,他也会通过循环补齐的方式延展为一个向量。
> f<-function(x,c){
+ return ((x+c)^2)
+ }
> f(1:3,0)
[1] 1 4 9#这意味着f()可以使用显式的向量给c赋值
f(1:3,1:3)
[1] 4 16 36如果想把c限制为1个标量
> f<-function(x,c){
+ if(length(c)!=1)
+ stop("vector c not allowed")
+ return((x+c)^2)
+ }
由以上例子可以总结出以下结论
1.使用向量化的运算符会使得函数也向量化
2. 内置函数和运算符号都可以实现向量化操作,运算符其实是一种函数,这种将运算符作为函数使用的方式被称为函数调用运算符。
内容持续更新中~💖💖💖💖
相关文章:
)
R语言易错点(持续更新中~~)
1.R向量元素的索引(下标)是从1开始的,而非0 >x [1] 1 2 4>x[3] [1] 4 2.[]和[ [ ] ] mylist<-list(stud.id1234,stud.name"Tom",stud.marksc(10,3,14,25,19)) > mylist $stud.id [1] 1234$stud.name [1] "Tom"$stud.marks [1] 10…...
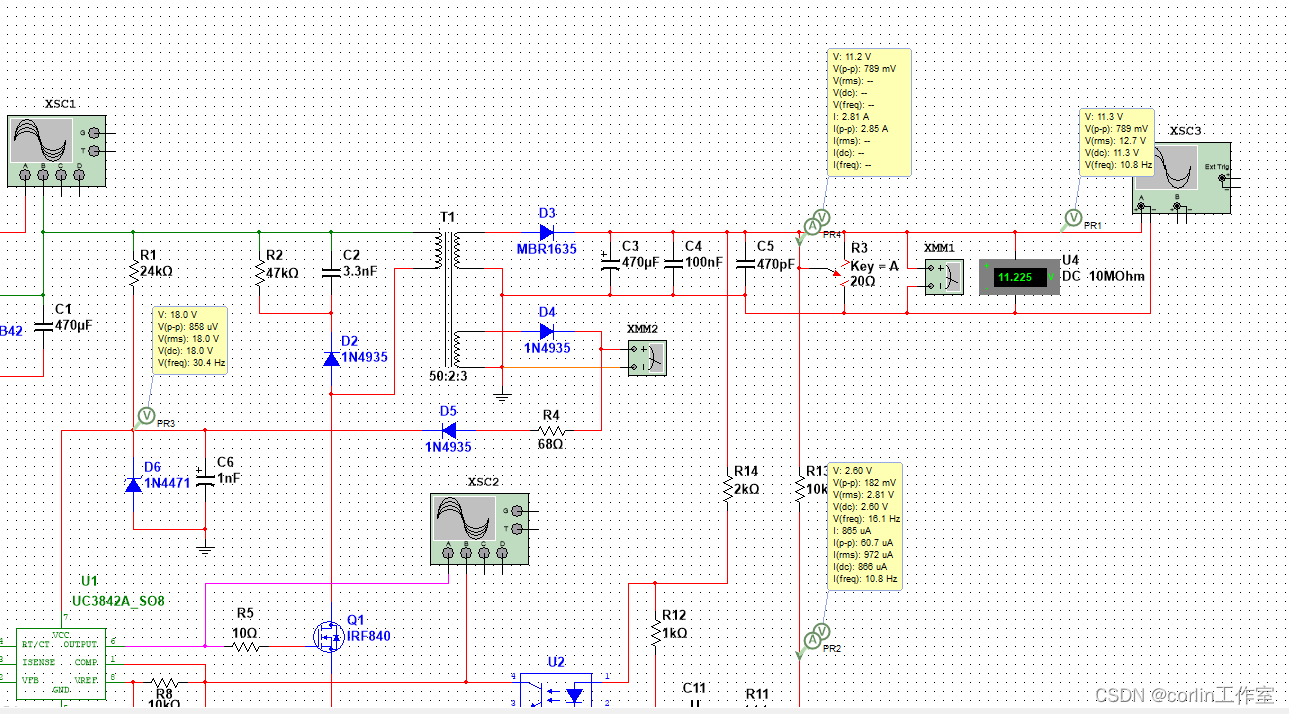
Multisim14.0仿真(二十七)基于UC3842的反激式开关电源的设计及仿真
一、UC3842简介: UC3842为固定频率电流模式PWM控制器。它们是专门为OFF−线和直流到直流转换器应用与最小的外部组件。内部实现的电路包括用于精确占空比控制的修剪振荡器、温度补偿参考、高增益误差放大器、电流传感比较器和理想适合于驱动功率MOSFET的高电流温度极…...

SpringMVC(二)@RequestMapping注解
我们先新建一个Module。 我们的依赖如下所示: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaL…...
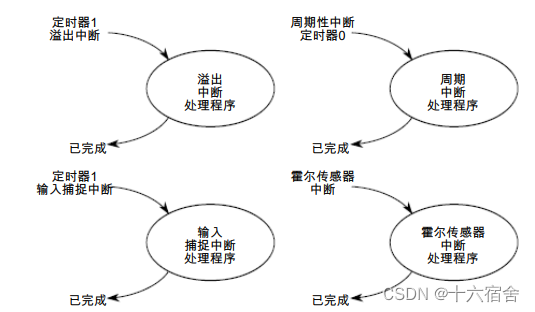
NXP公司K60N512+PWM控制BLDC电机
本篇文章介绍了使用NXP公司提供的塔式快速原型系统来驱动控制带霍尔传感器的无刷直流电机。文章涉及的塔式快速原型系统主要包括以下四个独立板卡:1.塔式系统支撑模块(TWR-Elevator),用以连接微控制器以及周边模块;2.低…...
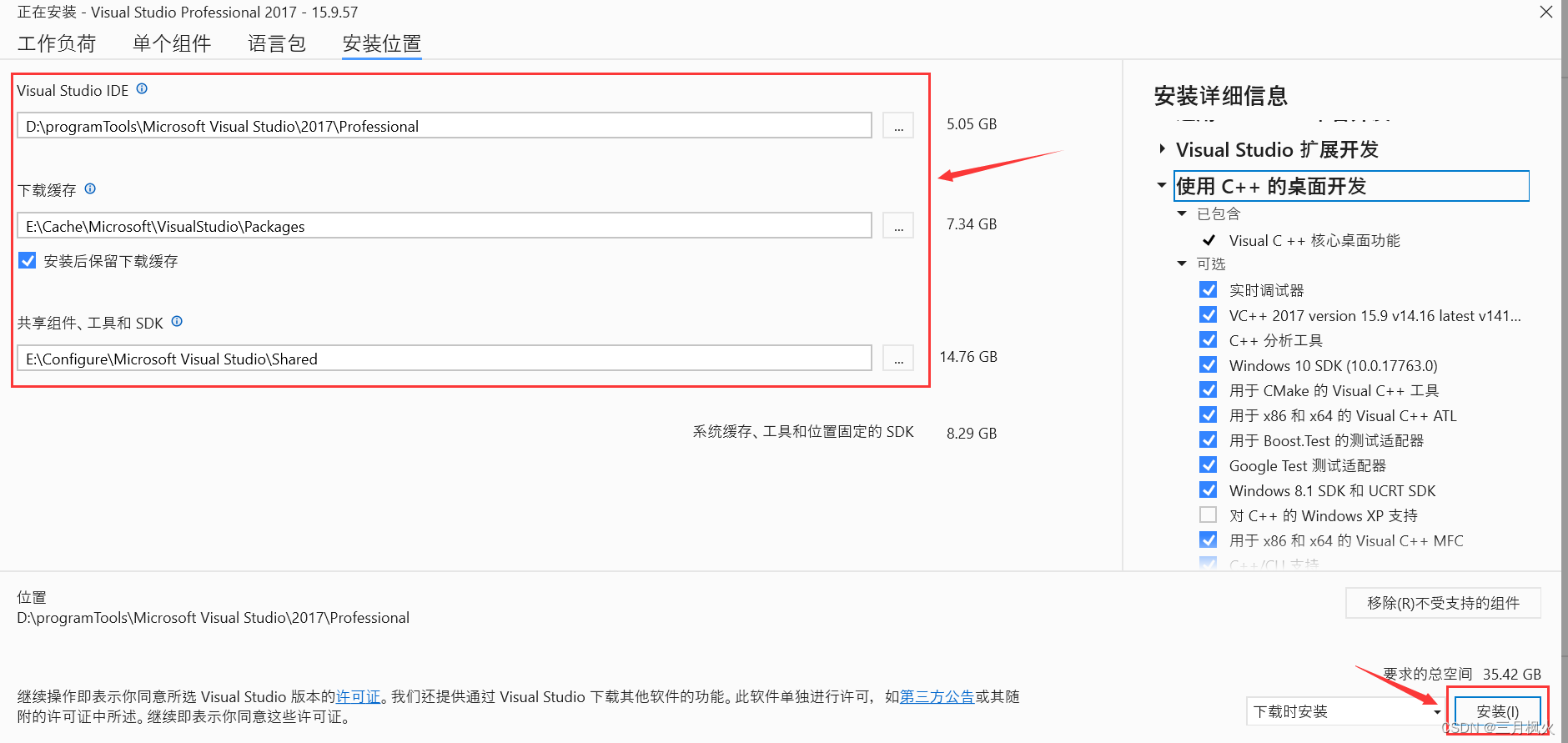
CAA的VS Studio安装
文章目录 一、官网下载VS Studio二、勾选如下安装信息三、更改软件安装位置四、17专业版密钥 一、官网下载VS Studio 官网下载地址: https://visualstudio.microsoft.com/zh-hans/downloads/ 下载对应版本后,以VS Studio2017为例: 二、勾…...
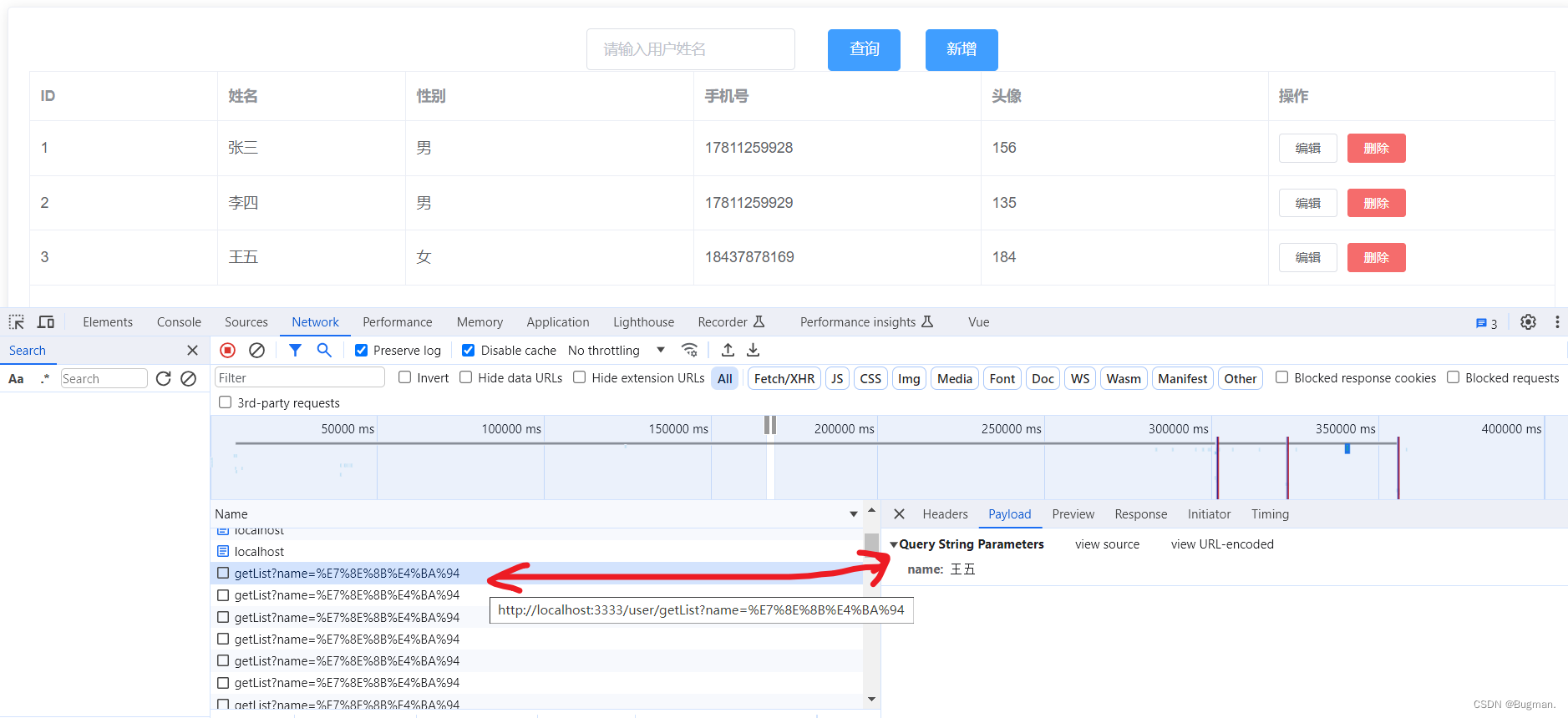
条件查询和数据查询
一、后端 1.controller层 package com.like.controller;import com.like.common.CommonDto; import com.like.entity.User; import com.like.service.UserService; import jakarta.annotation.Resource; import org.springframework.web.bind.annotation.GetMapping; import …...
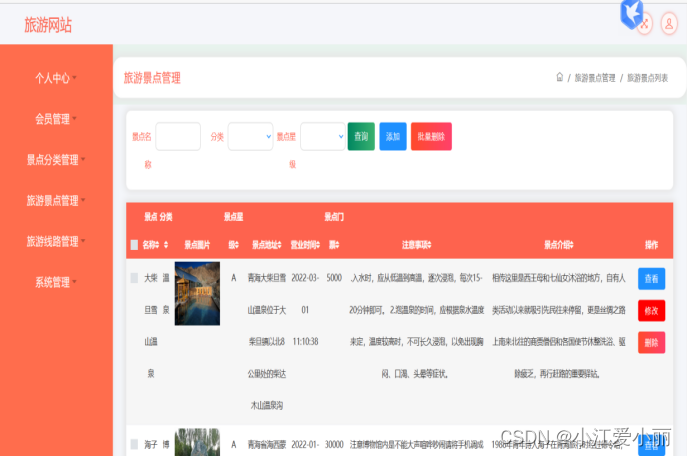
JSP旅游平台管理
本系统采用基于JAVA语言实现、架构模式选择B/S架构,Tomcat7.0及以上作为运行服务器支持,基于JAVA、JSP等主要技术和框架设计,idea作为开发环境,数据库采用MYSQL5.7以上。 开发环境: JDK版本:JDK1.8 服务器&…...
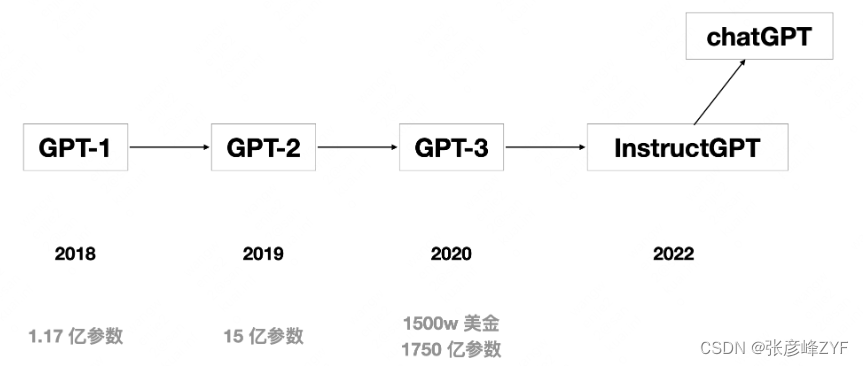
简单走近ChatGPT
目录 一、ChatGPT整体背景认知 (一)ChatGPT引起关注的原因 (二)与其他公司的竞争情况 二、NLP学习范式的发展 (一)规则和机器学习时期 (二)基于神经网络的监督学习时期 &…...

10.3作业
#include <myhead.h> int main(int argc, const char *argv[]) { mkfifo(“./f1”,0777); mkfifo(“./f2”,0777); pid_t cpid fork(); if(0 < cpid) { int fdw open(“./f1”,O_WRONLY); int fdr open(“./f2”,O_RDONLY); char buf[128] “”; while(1) { bzero…...

Springboot中的@Import注解~
Import注解是Spring框架中的注解之一,用于导入其他配置类或者组件 Import注解的作用有以下几点: 导入其他配置类:可以使用Import注解导入其他的配置类,将其加入到当前配置类中,从而可以共享配置信息 导入其他组件&am…...
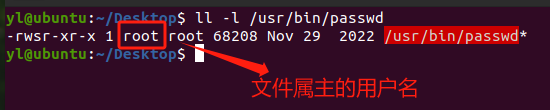
Linux 安全 - SUID机制
文章目录 一、文件权限位二、SUID简介 一、文件权限位 (1) $ ls -l text.txt -rw-rw-r-- 1 yl yl 0 Sep 28 16:25 text.txt其中第一个字段-rw-rw-r–,我们可以把它分为四部分看: -rw-rw-r--(1)- &a…...
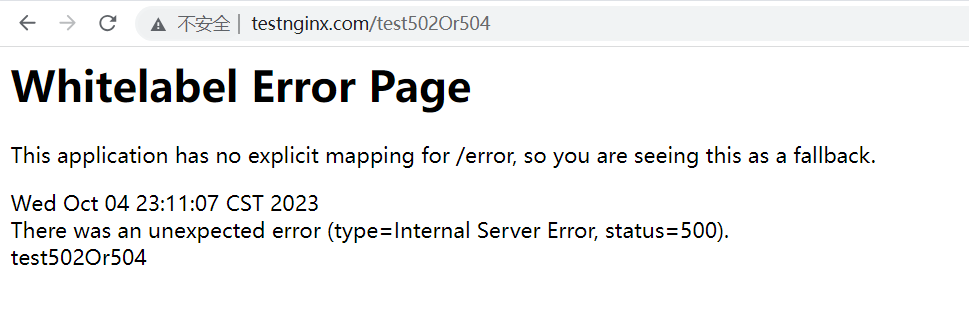
Nginx与Spring Boot的错误模拟实践:探索502和504错误的原因
文章目录 前言502和504区别---都是Nginx返回的access.log和error.log介绍SpringBoot结合Nginx实战502 and 504准备工作Nginx配置host配置SpringBoot 502模拟access.logerror.log 504模拟access.logerror.log 500模拟access.logerror.log 总结 前言 刚工作那会,最常…...
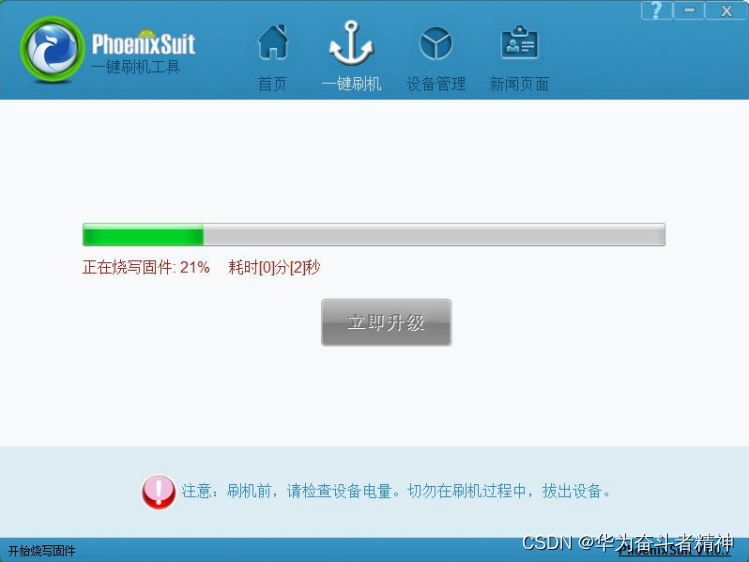
全志ARM926 Melis2.0系统的开发指引①
全志ARM926 Melis2.0系统的开发指引① 1. 编写目的2. Melis2.0 系统概述3. Melis2.0 快速开发3.1. Melis2.0 SDK 目录结构3.2. Melis2.0 编译环境3.3. Melis2.0 固件打包3.4. Melis2.0 固件烧录3.5.串口打印信息3.6. Melis2.0 添加和调用一个模块3.6.1. 为什么划分模块…...
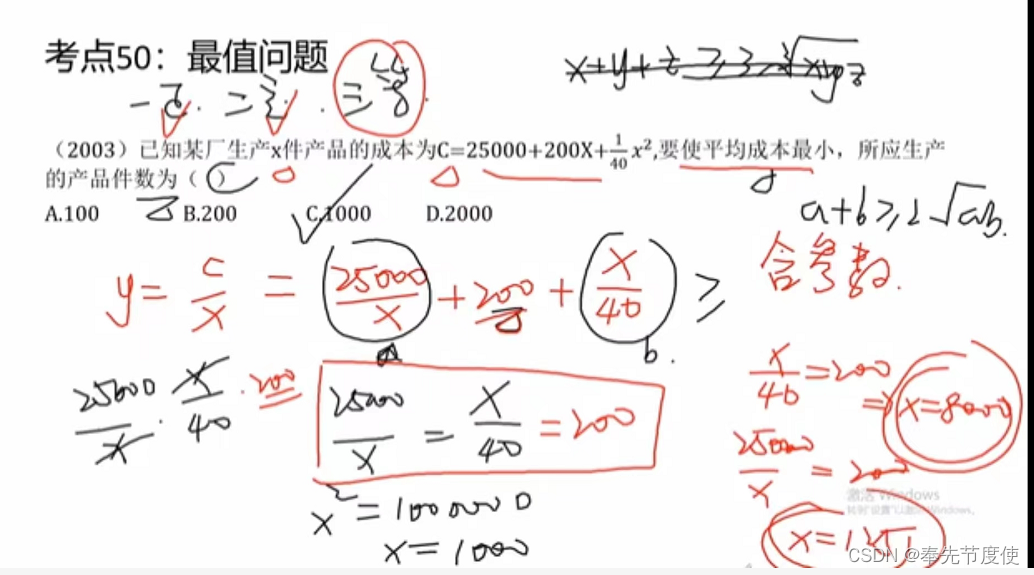
2024级199管理类联考之数学基础(下篇)
平面几何(平均2题) 三角形(性质、特殊三角形、全等与相似) 性质 由不在同一直线的三条线段首尾依次连接所组成的图形三条边、三个内角、三个定点三角形内角和为180度,外角和为360度,多边形的外角和为360度,n多边形的内角和为(n-2)*180度一个外角等于不相邻的两个内角之和任意…...

HTML之如何下载网页中的音频(二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...
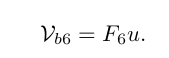
【现代机器人学】学习笔记十四:中文版印刷/翻译勘误
首先声明,这个印刷/勘误并非经过官方的认可,只是我个人的粗浅的理解。如果内容有误,恳请大家谅解指正。 其实有的并不算错,只是我个人认为不太准确,在我学习过程中产生了一些小疑惑和误解。 都是一些小毛病ÿ…...
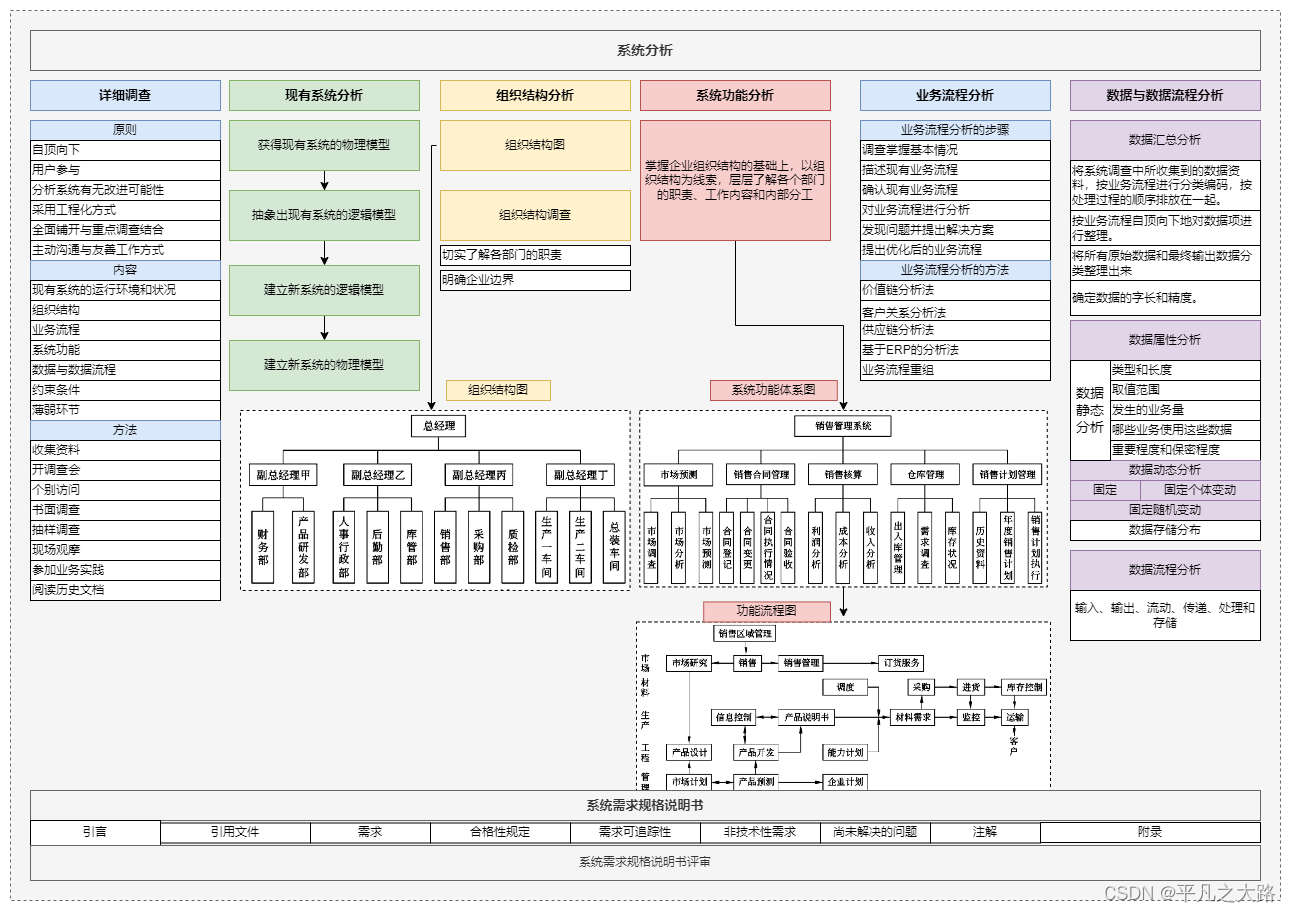
[架构之路-229]:计算机体硬件与系结构 - 计算机系统的矩阵知识体系结构
目录 一、纵向:目标系统的分层结构 1.1 目标系统的架构 1.2 网络协议栈 1.3 计算机程序语言分层 二、横向(构建目标系统的时间、开发阶段):软件工程 三、二维矩阵知识体系结构 一、纵向:目标系统的分层结构 1.1…...
第一章 visual studio下载安装
一、官网下载 地址:https://visualstudio.microsoft.com/zh-hans/ 点击免费visual studio 二、安装 运行下载好的exe文件,自定义安装目录 三、选择需要的组件安装 只需要选择标记组件,然后点击安装 等待安装完成就行 四、重启电脑 安装完之后…...

【服务器】在 Linux CLI 下安装 Anaconda
【服务器】在 Linux CLI 下安装 Anaconda 1 系统环境2 下载安装包3 安装 1 系统环境 查看系统信息 cat /etc/os-release2. 查看架构 uname -a # output # Linux localhost.localdomain 4.18.0-193.28.1.el8_2.x86_64 #1 SMP Thu Oct 22 00:20:22 UTC 2020 x86_64 x86_64 x86…...

Python中Lambda用法
在Python中,lambda函数是一种形式较短的函数,又称为匿名函数。与正常的函数不同,lambda函数没有名称,因此只能在定义时直接传递给其他函数或变量使用,而不能单独调用。 lambda函数的语法非常简单,格式如下…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
