二项分布以及实现
文章目录
- 前言
- 所谓二项分布就是只会产生两种结果的概率
- 1.概念
前言
所谓二项分布就是只会产生两种结果的概率
1.概念


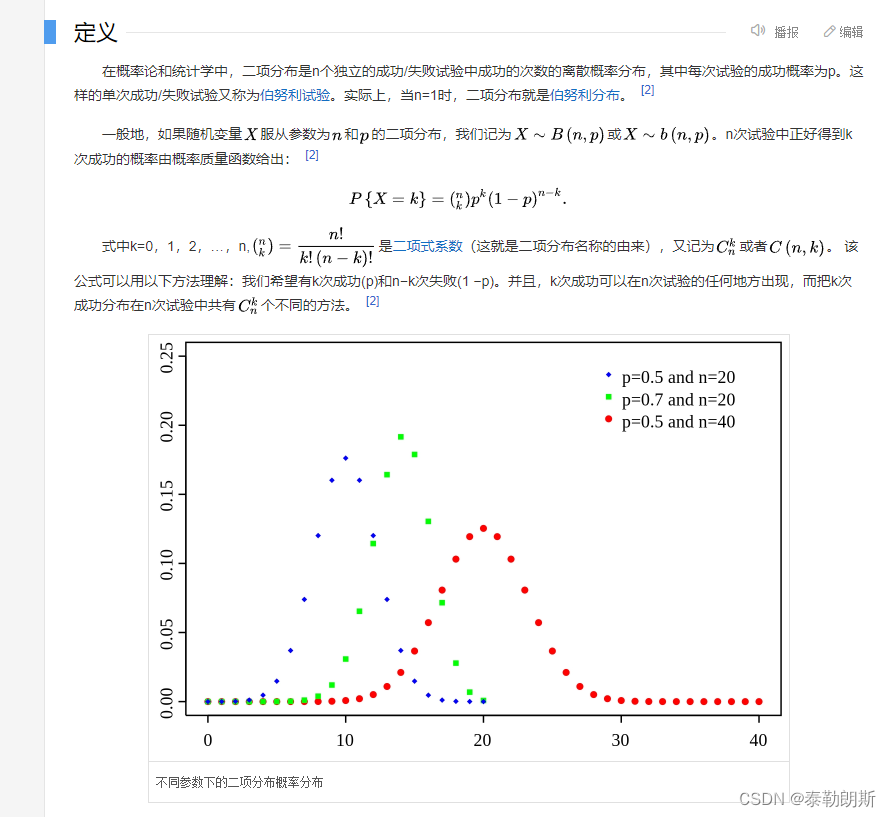
下面是一个二项分布的的theano实现
import numpy as np
import theano
import theano.tensor as T
from theano.tensor.nnet import conv
from theano.tensor.nnet import softmax
from theano.tensor import shared_randomstreamsx=T.matrix('x')
y =T.fscalars('y')theano.config.floatX='float32'# def dropout_layer(x,y):
# srng=shared_randomstreams.RandomStreams(np.random.RandomState(0).randint(999))
# mask=srng.binomial(n=1,p=1-y,size=x.shape)
# return x*T.cast(mask,theano.config.floatX)a=np.random.randn(2,3)srng=shared_randomstreams.RandomStreams(np.random.RandomState(0).randint(999))
mask=srng.binomial(n=1,p=1-y,size=x.shape)
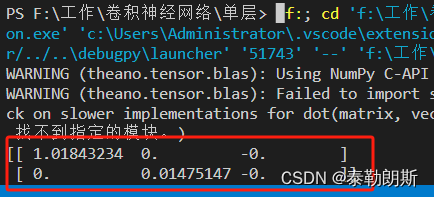
d=x*T.cast(mask,theano.config.floatX)fun=theano.function([x,y],d)print(fun(a,0.6))结果:
可以看到要么是0,要么是1,当然是近似
相关文章:

二项分布以及实现
文章目录 前言所谓二项分布就是只会产生两种结果的概率 1.概念 前言 所谓二项分布就是只会产生两种结果的概率 1.概念 下面是一个二项分布的的theano实现 import numpy as np import theano import theano.tensor as T from theano.tensor.nnet import conv from theano.ten…...

css自学框架之幻灯片展示效果
这一节,我自学了焦点图效果(自动播放,圆点控制),首先看一下效果: 下面我们还是老思路,css展示学习三个主要步骤:一是CSS代码,二是Javascript代码,三是Html代码。 一、css代码主要如…...

坦克世界WOT知识图谱三部曲之爬虫篇
文章目录 关于坦克世界1. 爬虫任务2. 获取坦克列表3. 获取坦克具体信息结束语 关于坦克世界 《坦克世界》(World of Tanks, WOT)是我在本科期间玩过的一款战争网游,由Wargaming公司研发。2010年10月30日在俄罗斯首发,2011年4月12日在北美和欧洲推出&…...
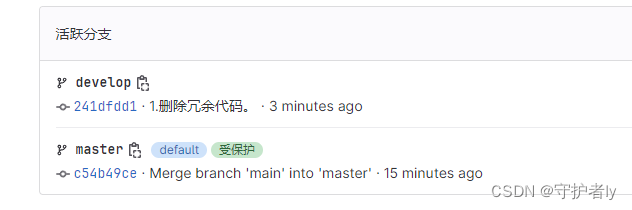
Idea上传项目到gitlab并创建使用分支
Idea上传项目到gitlab并创建使用分支 1 配置git 在idea的setting中,找到git,配置好git的位置,点击Test按钮显示出git版本号,则说明配置成功。 2 项目中引入git Idea通过VCS,选择Create Git Repository 在弹出的对话框…...
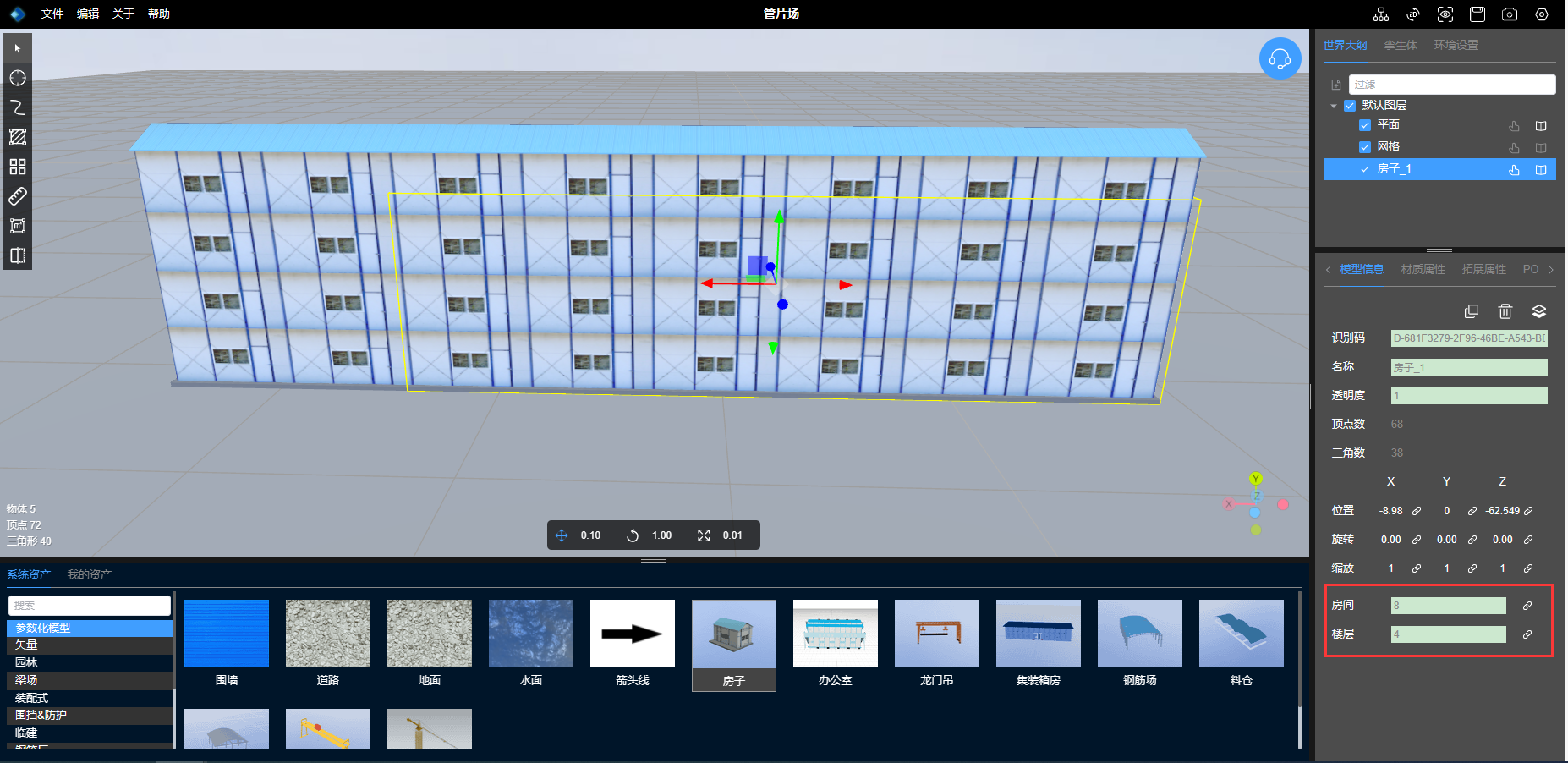
3D孪生场景搭建:参数化模型
1、什么是参数化模型 参数化模型是指通过一组参数来定义其形状和特征的数学模型或几何模型。这些参数可以用于控制模型的大小、形状、比例、位置、旋转、曲率等属性,从而实现对模型进行灵活的调整和变形。 在计算机图形学和三维建模领域,常见的参数化模…...

最短路径专题6 最短路径-多路径
题目: 样例: 输入 4 5 0 2 0 1 2 0 2 5 0 3 1 1 2 1 3 2 2 输出 2 0->1->2 0->3->2 思路: 根据题意,最短路模板还是少不了的, 我们要添加的是, 记录各个结点有多少个上一个结点走动得来的…...

【Linux】Linux常用命令—文件管理(上)
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c系列专栏:C/C零基础到精通 🔥 给大…...
【Python】基于OpenCV人脸追踪、手势识别控制的求生之路FPS游戏操作
【Python】基于OpenCV人脸追踪、手势识别控制的求生之路FPS游戏操作 文章目录 手势识别人脸追踪键盘控制整体代码附录:列表的赋值类型和py打包列表赋值BUG复现代码改进优化总结 py打包 视频: 基于OpenCV人脸追踪、手势识别控制的求实之路FPS游戏操作 手…...
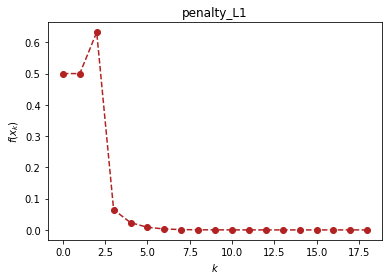
约束优化算法(optimtool.constrain)
import optimtool as oo from optimtool.base import np, sp, pltpip install optimtool>2.4.2约束优化算法(optimtool.constrain) import optimtool.constrain as oc oc.[方法名].[函数名]([目标函数], [参数表], [等式约束表], [不等式约数表], [初…...
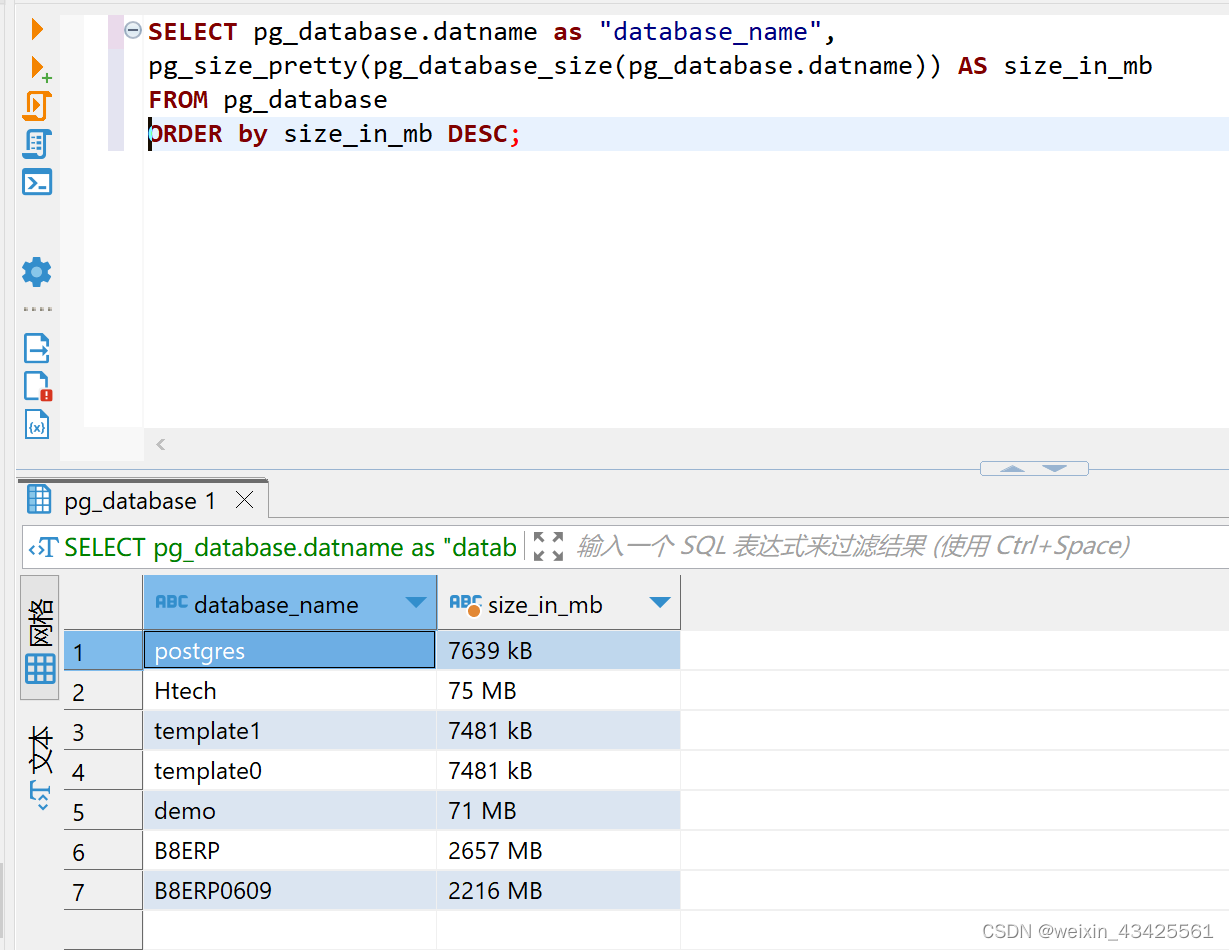
如何查看postgresql中的数据库大小?
你可以使用以下命令来查看PostgreSQL数据库的大小: SELECT pg_database.datname as "database_name", pg_size_pretty(pg_database_size(pg_database.datname)) AS size_in_mb FROM pg_database ORDER by size_in_mb DESC;这将返回一个表格࿰…...

使用python-opencv检测图片中的人像
最简单的方法进行图片中的人像检测 使用python-opencv配合yolov3模型进行图片中的人像检测 1、安装python-opencv、numpy pip install opencv-python pip install numpy 2、下载yolo模型文件和配置文件: 下载地址: https://download.csdn.net/down…...

项目进展(三)-电机驱动起来了,发现了很多关键点,也遇到了一些低级错误,
一、前言 昨天电机没有驱动起来,头发掉一堆,不过今天,终于终于终于把电机驱动起来了!!!!,特别开心,哈哈哈哈,后续继续努力完善!!&…...
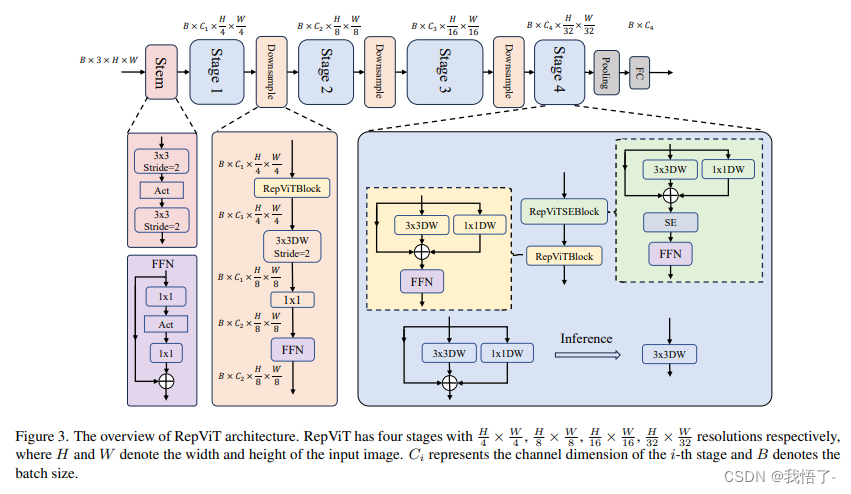
目标检测算法改进系列之Backbone替换为RepViT
RepViT简介 轻量级模型研究一直是计算机视觉任务中的一个焦点,其目标是在降低计算成本的同时达到优秀的性能。轻量级模型与资源受限的移动设备尤其相关,使得视觉模型的边缘部署成为可能。在过去十年中,研究人员主要关注轻量级卷积神经网络&a…...

学习 Kubernetes的难点和安排
Kubernetes 技术栈的特点可以用四个字来概括,那就是“新、广、杂、深”: 1.“新”是指 Kubernetes 用到的基本上都是比较前沿、陌生的技术,而且版本升级很快,经常变来变去。 2.“广”是指 Kubernetes 涉及的应用领域很多、覆盖面非…...

【MATLAB源码-第42期】基于matlab的人民币面额识别系统(GUI)。
操作环境: MATLAB 2022a 1、算法描述 基于 MATLAB 的人民币面额识别系统设计可以分为以下步骤: 1. 数据收集与预处理 数据收集: 收集不同面额的人民币照片,如 1 元、5 元、10 元、20 元、50 元和 100 元。确保在不同环境、不…...
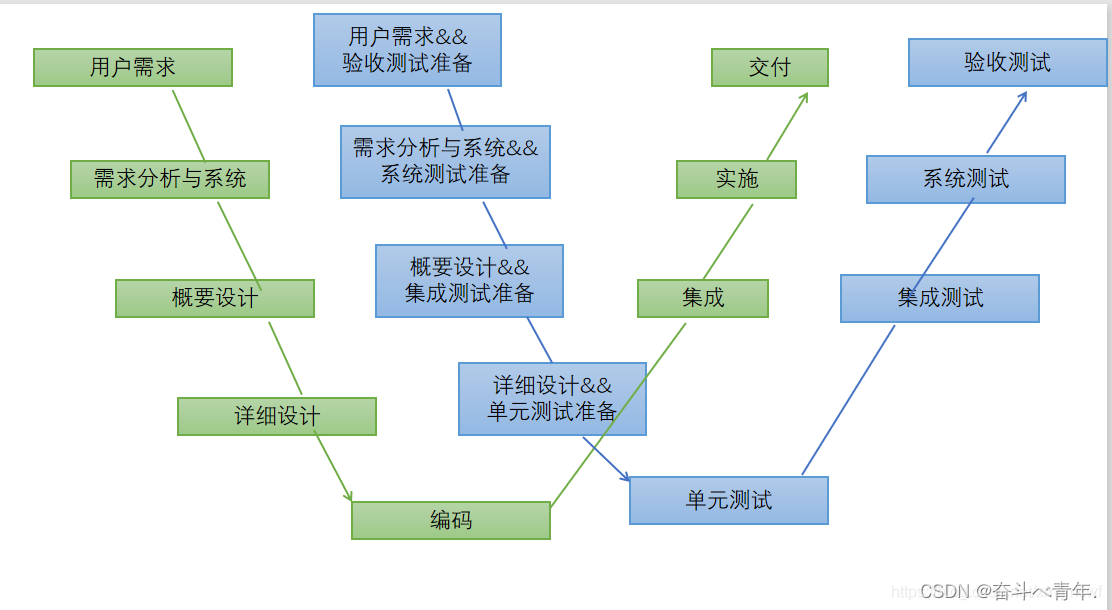
【软件测试】软件测试的基础概念
一、一个优秀的测试人员需要具备的素质 技能方面: 优秀的测试用例设计能力:测试用例设计能力是指,无论对于什么类型的测试,都能够设计出高效的发现缺陷,保证产品质量的优秀测试用例。这就需要我们掌握设计测试用例的方…...
Docker-mysql,redis安装
安装MySQL 下载MySQL镜像 终端运行命令 docker pull mysql:8.0.29镜像下载完成后,需要配置持久化数据到本地 这是mysql的配置文件和存储数据用的目录 切换到终端,输入命令,第一次启动MySQL容器 docker run --restartalways --name mysq…...

五种I/O模型
目录 1、阻塞IO模型2、非阻塞IO模型3、IO多路复用模型4、信号驱动IO模型5、异步IO模型总结 blockingIO - 阻塞IOnonblockingIO - 非阻塞IOIOmultiplexing - IO多路复用signaldrivenIO - 信号驱动IOasynchronousIO - 异步IO 5种模型的前4种模型为同步IO,只有异步IO模…...

用nativescript开发ios程序常用命令?
NativeScript是一个用于跨平台移动应用程序开发的开源框架,允许您使用JavaScript或TypeScript构建原生iOS和Android应用程序。以下是一些常用的NativeScript命令,用于开发iOS应用程序: 1、创建新NativeScript项目: tns create m…...
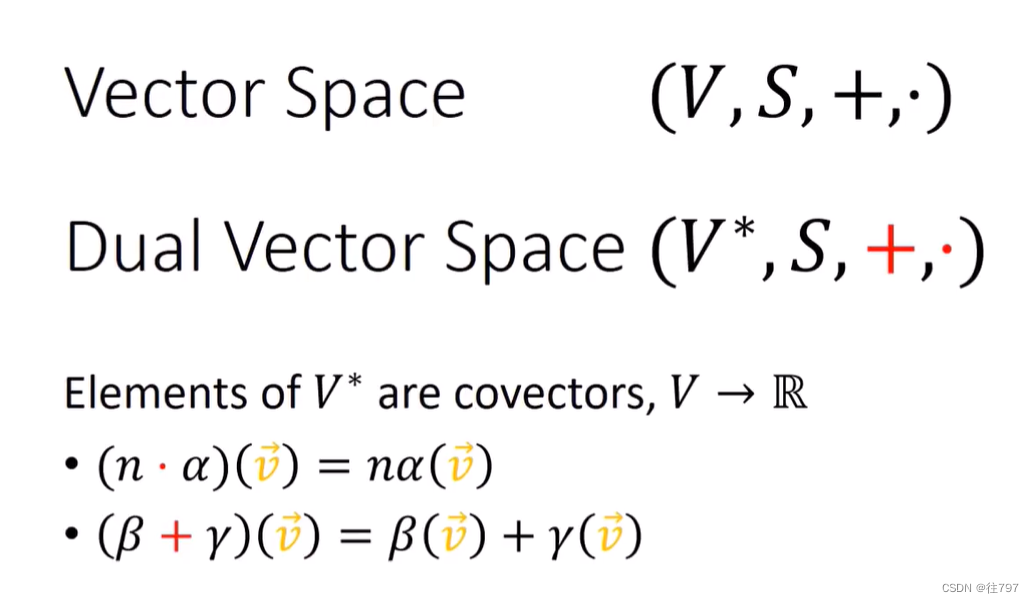
6.Tensors For Beginners-What are Convector
Covectors (协向量) What‘s a covector Covectors are “basically” Row Vectors 在一定程度上,可认为 协向量 基本上就像 行向量。 但不能简单地认为 这就是列向量进行转置! 行向量 和 列向量 是根本不同类型的对象。 …...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
