图示矩阵分解
特征值与特征向量
设 A A A 是 n 阶矩阵,如果存在数 λ \lambda λ 和 n 维非零列向量 x x x,满足关系式:
A x = λ x ( 1 ) Ax = \lambda x\quad\quad(1) Ax=λx(1)
则数 λ \lambda λ 称为矩阵 A A A 的特征值,非零向量 x x x 称为矩阵 A A A 的特征向量.
关系式(1)推导得到 ( A − λ E ) x = 0 (A - \lambda E)x = 0 (A−λE)x=0,存在非零解 x x x 的充分必要条件为系数行列式为零:
∣ A − λ E ∣ = 0 ( 2 ) |A-\lambda E| = 0\quad\quad(2) ∣A−λE∣=0(2)
上式是以 λ \lambda λ 为未知数的一元 n 次方程,称为矩阵 A A A 的特征方程。特征方程在复数范围内恒有解,解的个数为方程的次数(重根按重数计算),因此,n 阶矩阵 A A A 在复数范围内有 n 个特征值。
设 n 阶矩阵 A = ( a i j ) A = (a_{ij}) A=(aij) 的特征值为 λ 1 , λ 2 , . . . , λ n \lambda_1, \lambda_2,...,\lambda_n λ1,λ2,...,λn
- ∑ i = 1 n λ i = ∑ i = 1 n a i i = t r ( A ) \sum_{i=1}^n\lambda_i = \sum_{i=1}^na_{ii} = tr(A) ∑i=1nλi=∑i=1naii=tr(A)
- ∏ i = 1 n λ i = ∣ A ∣ \prod_{i=1}^n\lambda_i = |A| ∏i=1nλi=∣A∣
- A 可逆的充分必要条件是 n 个特征值全不为零
有如下性质:
- 设 λ \lambda λ 是方阵 A A A 的特征值,则 λ 2 \lambda^2 λ2 是 A 2 A^2 A2 的特征值;当 A A A 可逆时, 1 / λ 1/\lambda 1/λ 是 A − 1 A^{-1} A−1的特征值.
A , B A,B A,B 都是 n 阶矩阵,若有可逆矩阵 P P P ,使:
P − 1 A P = B P^{-1}AP = B P−1AP=B
则称 B 是 A 的相似矩阵。 P − 1 A P P^{-1}AP P−1AP 称为 A 的相似变换。
定理:相似矩阵的特征值相同.
对于 n 阶矩阵 A , 若存在矩阵 P 满足 P − 1 A P = Λ P^{-1}AP =\Lambda P−1AP=Λ,则称矩阵 A 可对角化。
定理:一个 n 阶方阵 A 如果有 n 个不同的特征值,那么对应的 n 个特征向量互相线性独立
定理:任何 n 阶对称矩阵都有 n 个独立且正交的特征向量
图解特征值的含义:
| A | 特征值&特征向量 | x | Ax |
|---|---|---|---|
| [ 0.5 1 0 2 ] \begin{bmatrix} 0.5 & 1 \\ 0 & 2 \end{bmatrix} [0.5012] | λ 1 = 0.5 , p 1 = [ 1 , 0 ] T λ 2 = 2 , p 2 = [ 0 , 1 ] T \lambda_1 = 0.5, p_1 = [1, 0]^T \\ \lambda_2= 2, p_2 = [0, 1]^T λ1=0.5,p1=[1,0]Tλ2=2,p2=[0,1]T | 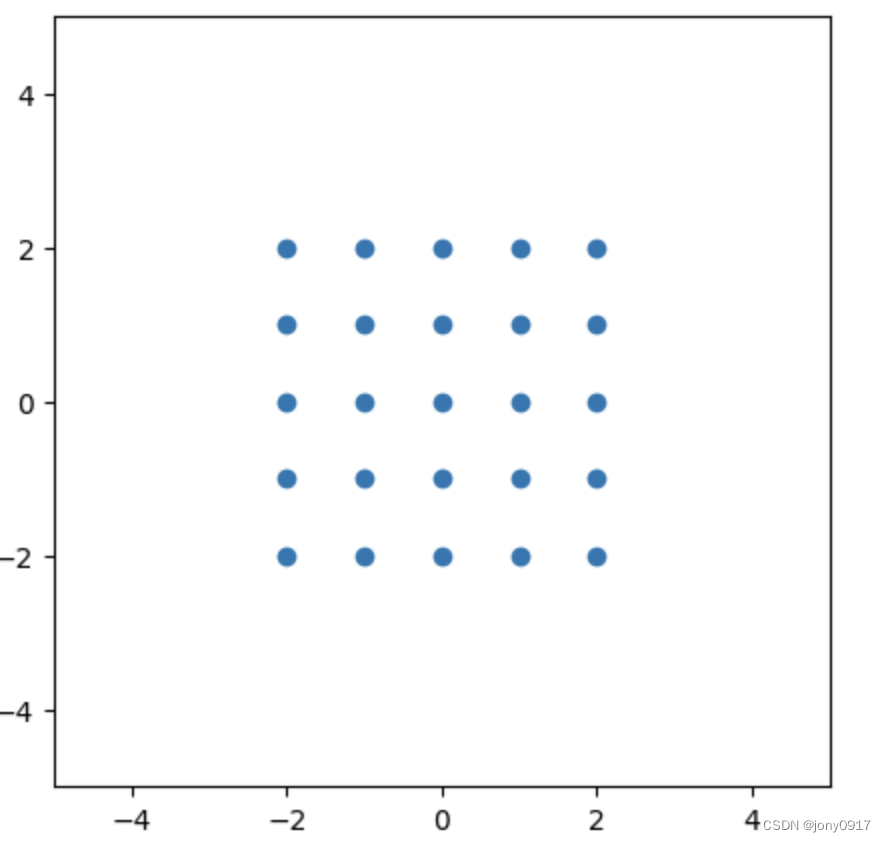 | 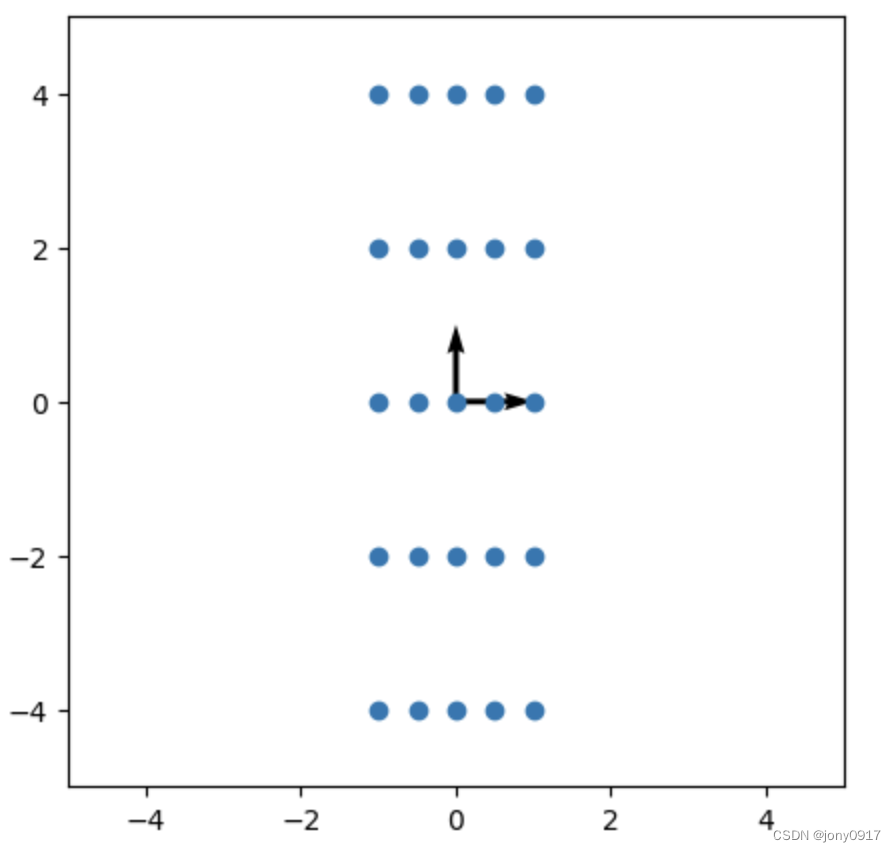 |
| [ 1 − 1 − 1 1 ] \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} [1−1−11] | λ 1 = 0 , p 1 = [ 1 , 1 ] T λ 2 = 2 , p 2 = [ − 1 , 1 ] T \lambda_1 = 0, p_1 = [1, 1]^T \\ \lambda_2= 2, p_2 = [-1, 1]^T λ1=0,p1=[1,1]Tλ2=2,p2=[−1,1]T |  | 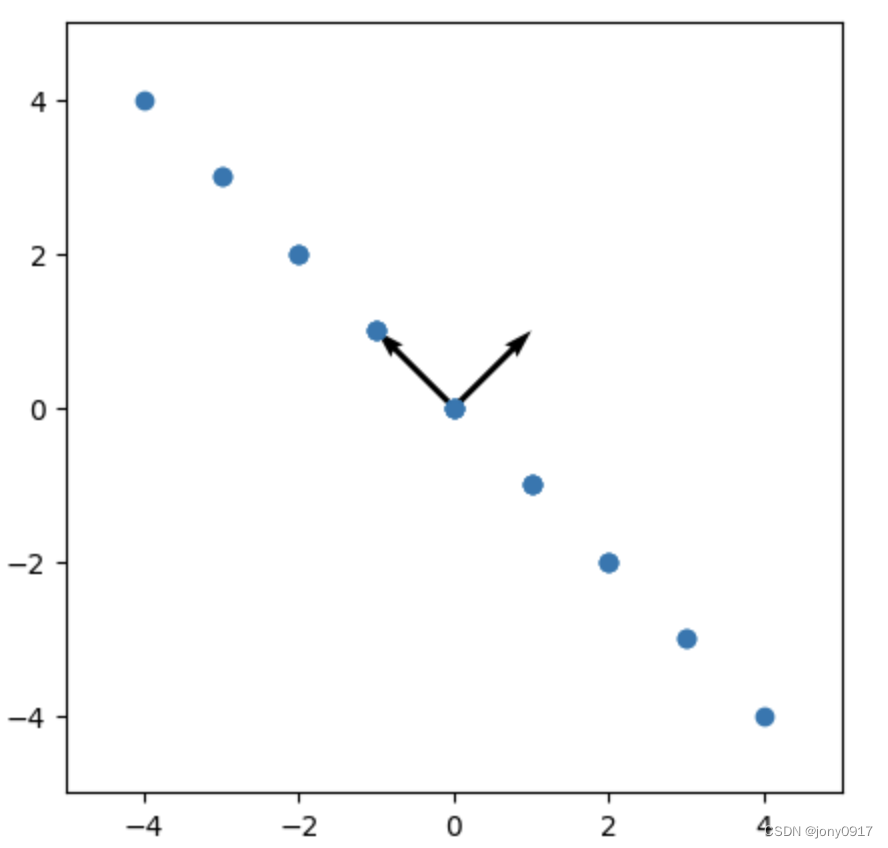 |
| [ 3 − 1 − 1 3 ] \begin{bmatrix} 3 & -1 \\ -1 & 3 \end{bmatrix} [3−1−13] | λ 1 = 2 , p 1 = [ 1 , 1 ] T λ 2 = 4 , p 2 = [ − 1 , 1 ] T \lambda_1 = 2, p_1 = [1, 1]^T \\ \lambda_2= 4, p_2 = [-1, 1]^T λ1=2,p1=[1,1]Tλ2=4,p2=[−1,1]T |  | 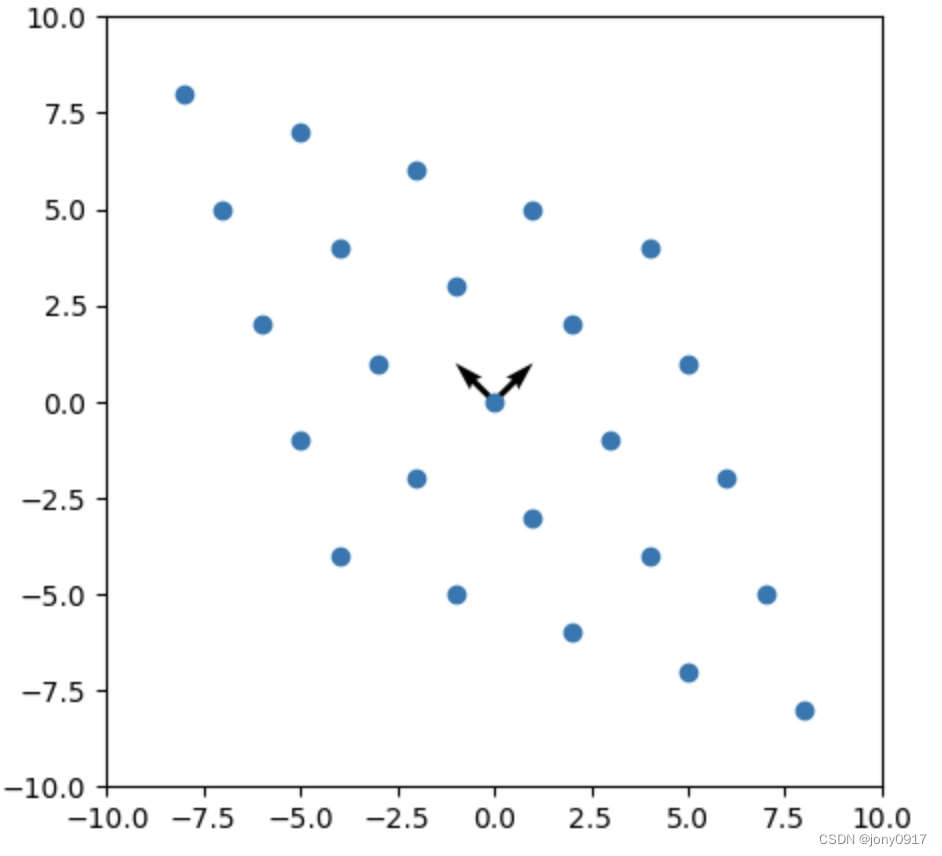 |
Cholesky 分解(Cholesky Decomposition)
把一个对称正定的矩阵表示成一个下三角矩阵 L 与其转置的乘积的形式。
A = L L T A = LL^T A=LLT
特征值分解(Eigen Decomposition)
对角化条件:当且仅当A满秩(有n个独立的特征向量)时,有 A = P − 1 D P A = P^{-1}DP A=P−1DP,P 为A的特征矩阵组成的可逆矩阵,D是有A的特征值组成的对角矩阵。
任何对称矩阵都可以对角化:
S = P D P − 1 S = PDP^{-1} S=PDP−1
其中 P 是由 n 个正交特征向量组成的矩阵,D 是有特征值组成的对角矩阵。
图解特征值分解:
| S = P D P − 1 S=PDP^{-1} S=PDP−1 | x | P − 1 x P^{-1}x P−1x | D P − 1 x DP^{-1}x DP−1x | P D P − 1 x PDP^{-1}x PDP−1x |
|---|---|---|---|---|
| [ 2 − 1 − 1 2 ] = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} = [2−1−12]= [ 1 1 1 − 1 ] [ 1 0 0 3 ] [ 1 2 1 2 1 2 − 1 2 ] \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix}\begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \end{bmatrix} [111−1][1003][212121−21] |  | 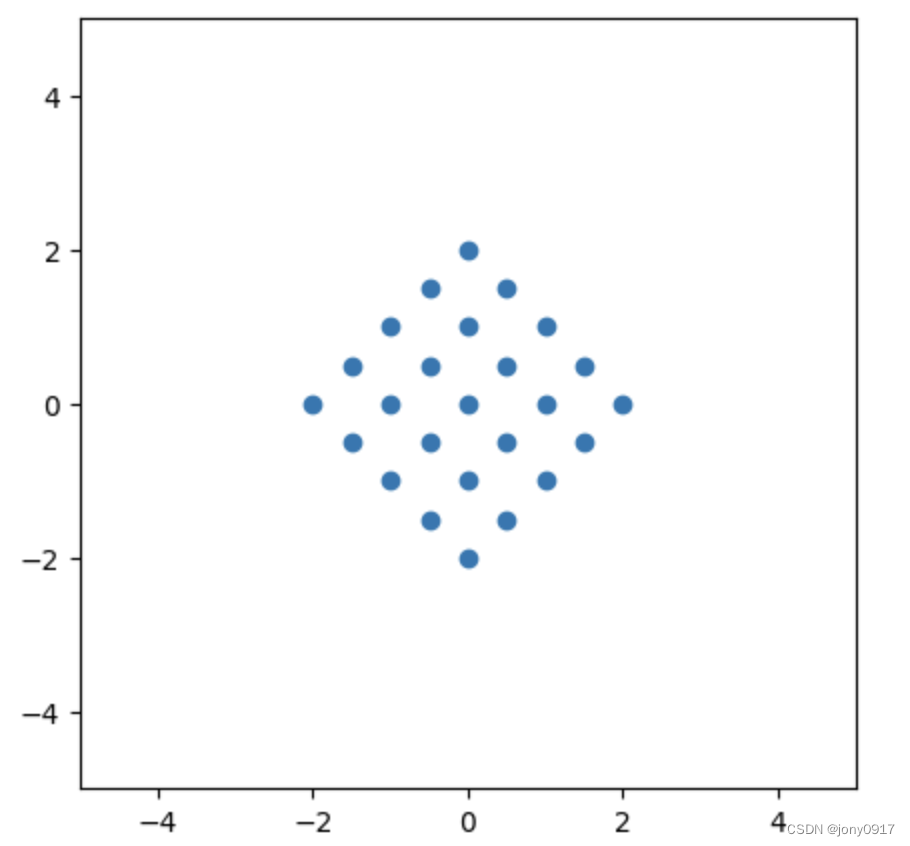 | 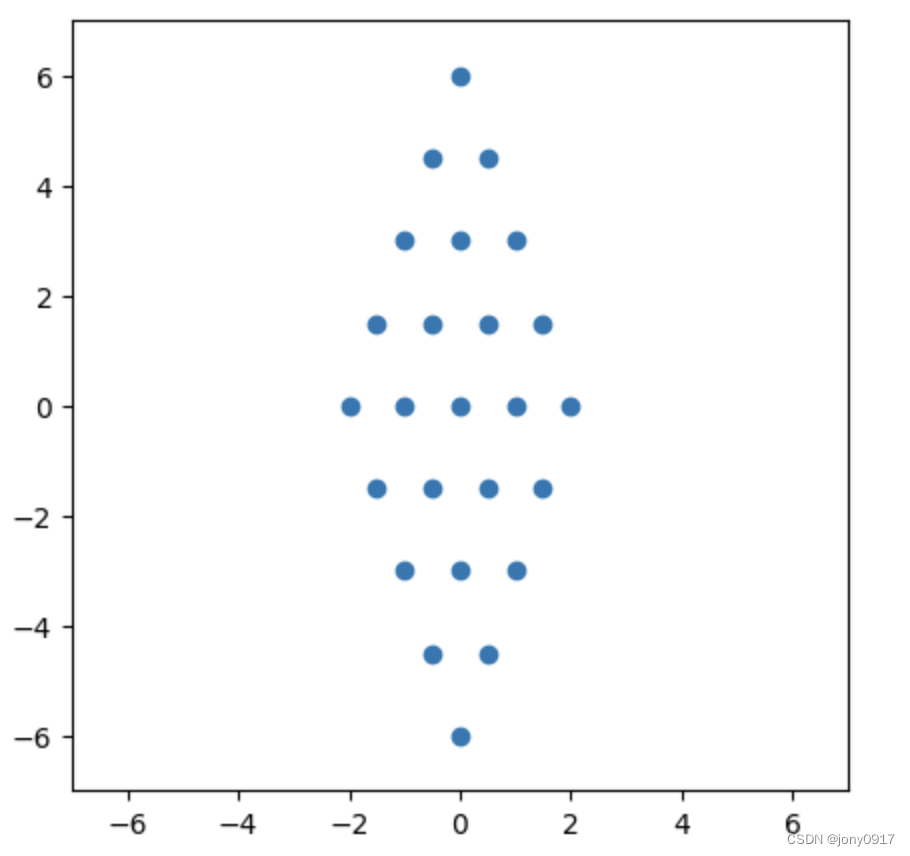 | 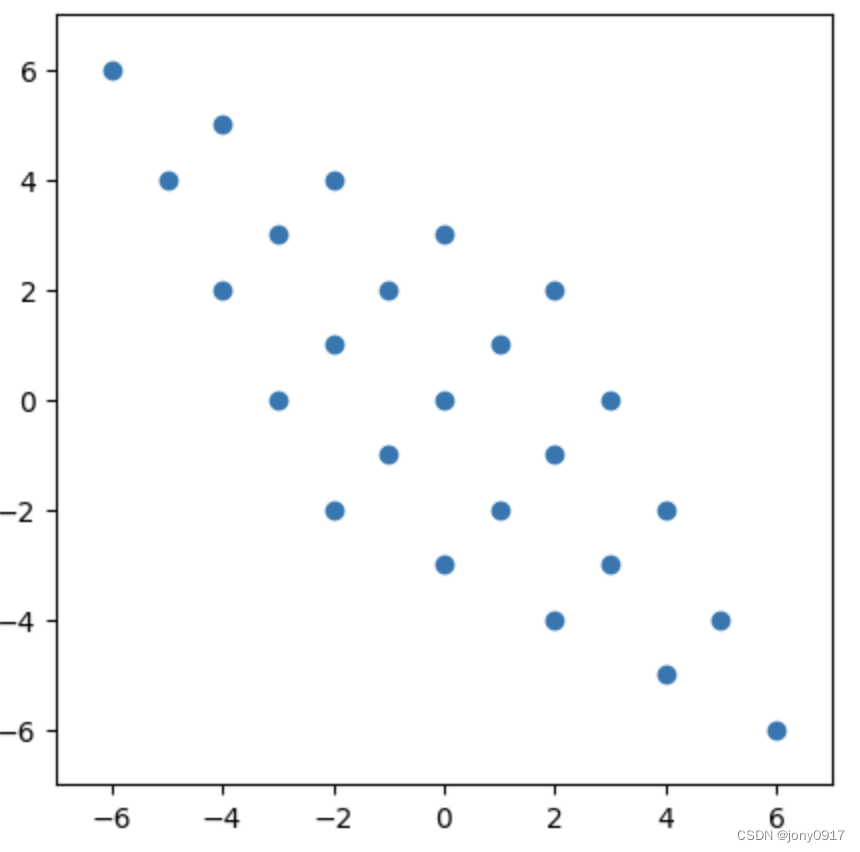 |
奇异值分解(Singular Value Decomposition)
SVD定理:设矩阵 A m × n A^{m\times n} Am×n 的秩为 r ∈ ( 0 , m i n ( m , n ) ) r\in (0, min(m,n)) r∈(0,min(m,n)),矩阵 A 的奇异值分解形式如下
A = U Σ V T A = U\Sigma V^T A=UΣVT
其中 U ∈ R m × m , V ∈ R n × n U\in R^{m\times m},V\in R^{n\times n} U∈Rm×m,V∈Rn×n 是正交矩阵, Σ ∈ R m × n \Sigma\in R^{m\times n} Σ∈Rm×n 满足 Σ i i = σ i ≥ 0 , Σ i j = 0 , i ≠ j \Sigma_{ii} = \sigma_i \ge 0, \Sigma_{ij} = 0, i\ne j Σii=σi≥0,Σij=0,i=j, σ i \sigma_i σi称为奇异值。
图解奇异值分解:
| A = U Σ V T A = U\Sigma V^T A=UΣVT | x | V T x V^Tx VTx | Σ V T x \Sigma V^T x ΣVTx | U Σ V T x U\Sigma V^T x UΣVTx |
|---|---|---|---|---|
| [ 1 1 1 1 0 0 ] = \begin{bmatrix} 1 & 1 \\ 1 & 1 \\ 0 & 0 \end{bmatrix} = 110110 = [ 1 2 − 1 2 0 1 2 1 2 0 0 0 1 ] [ 2 0 0 0 0 0 ] [ 1 2 − 1 2 1 2 1 2 ] T \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}^T 21210−21210001 200000 [2121−2121]T | 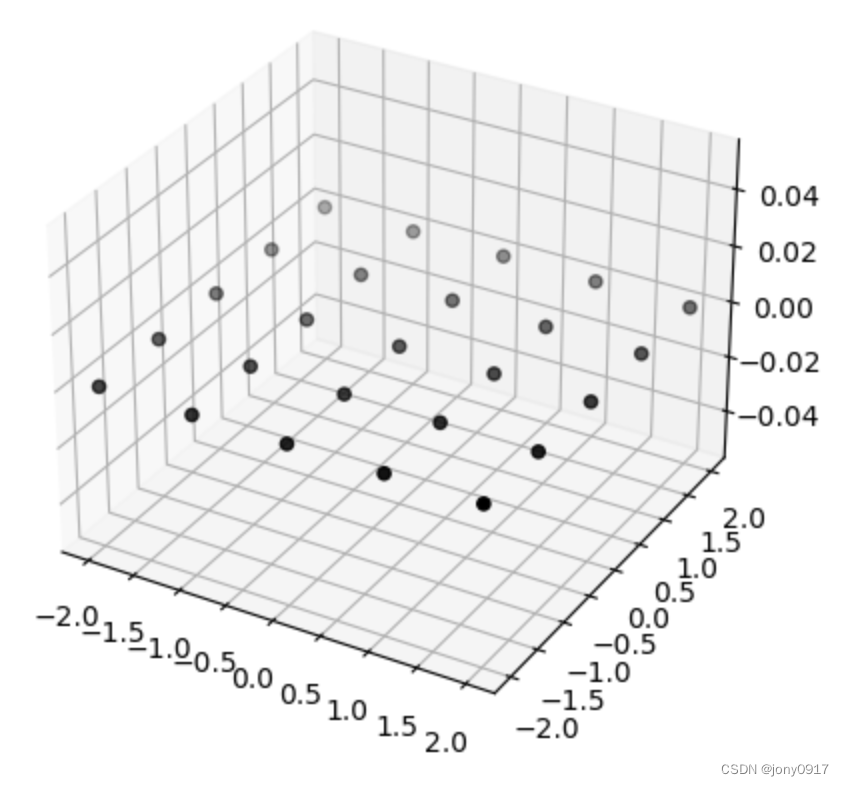 | 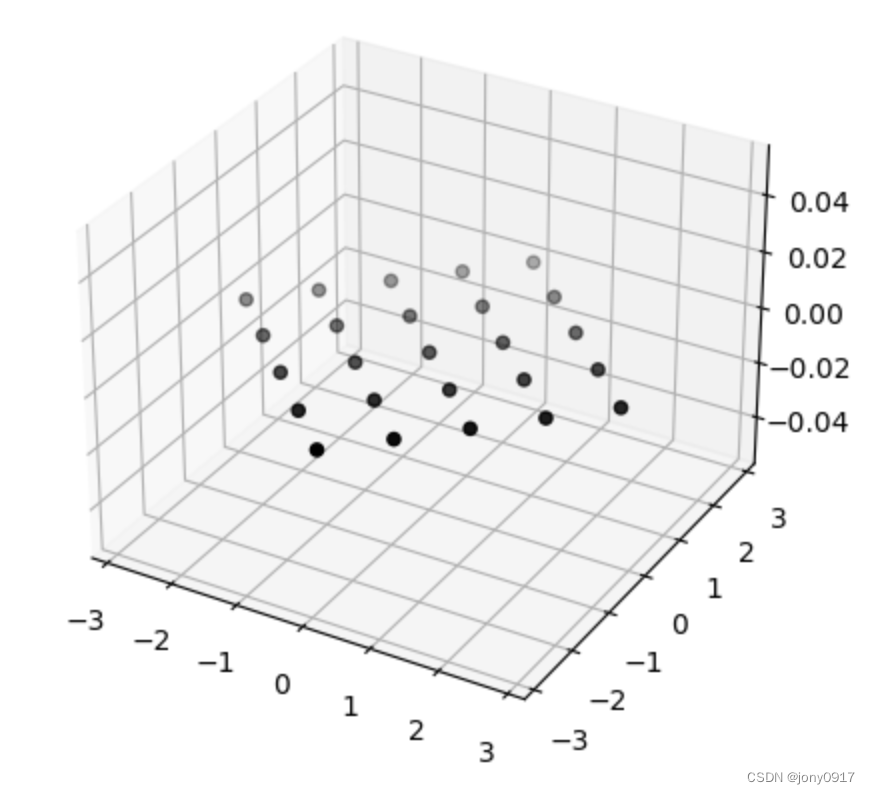 | 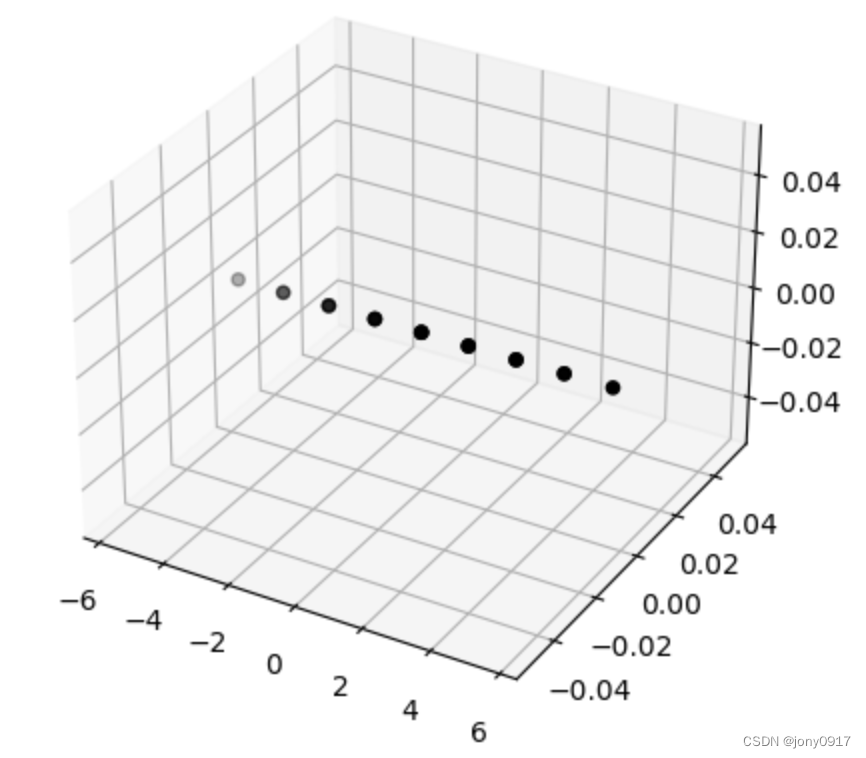 | 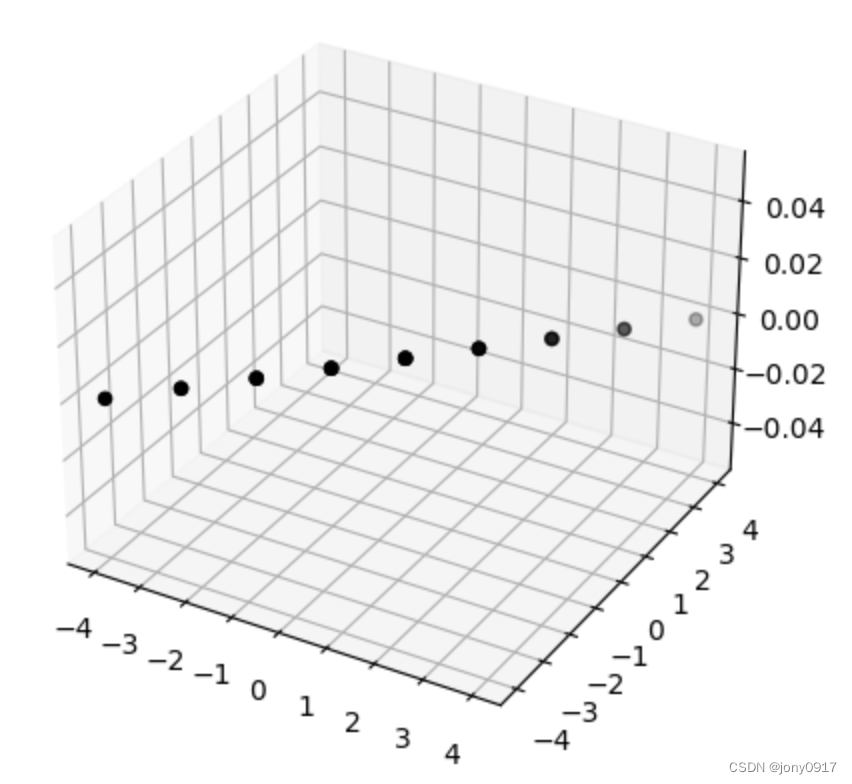 |
| [ 0 1 1 1 1 0 ] = \begin{bmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{bmatrix} = 011110 = [ 1 6 1 2 1 3 2 6 0 − 1 3 1 6 − 1 2 1 3 ] [ 3 0 0 1 0 0 ] [ 1 2 − 1 2 1 2 1 2 ] T \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{bmatrix}\begin{bmatrix} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}^T 616261210−2131−3131 300010 [2121−2121]T |  | 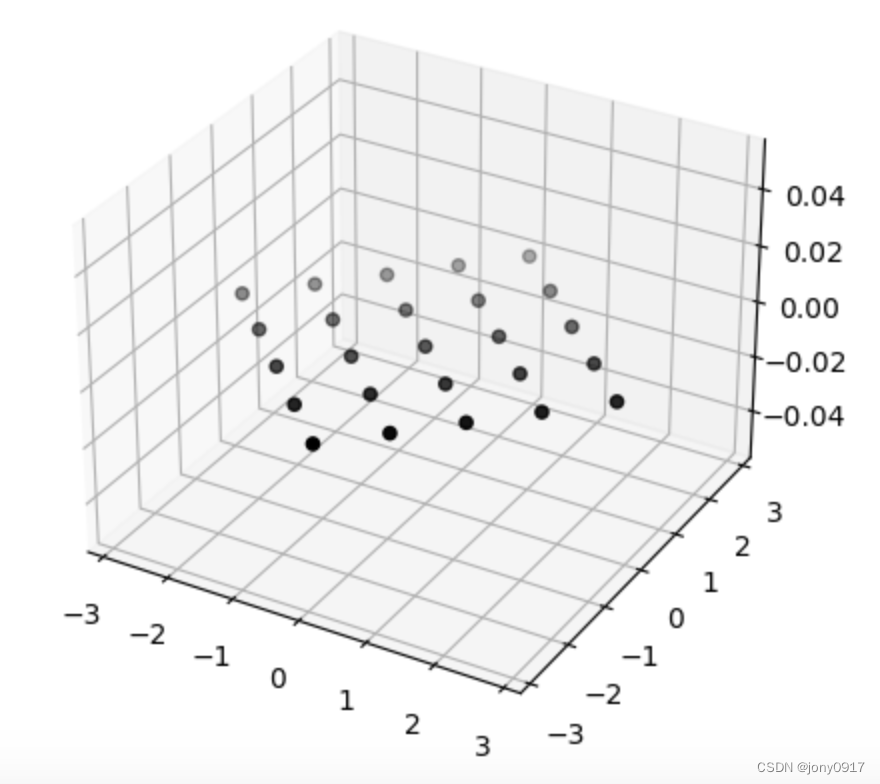 | 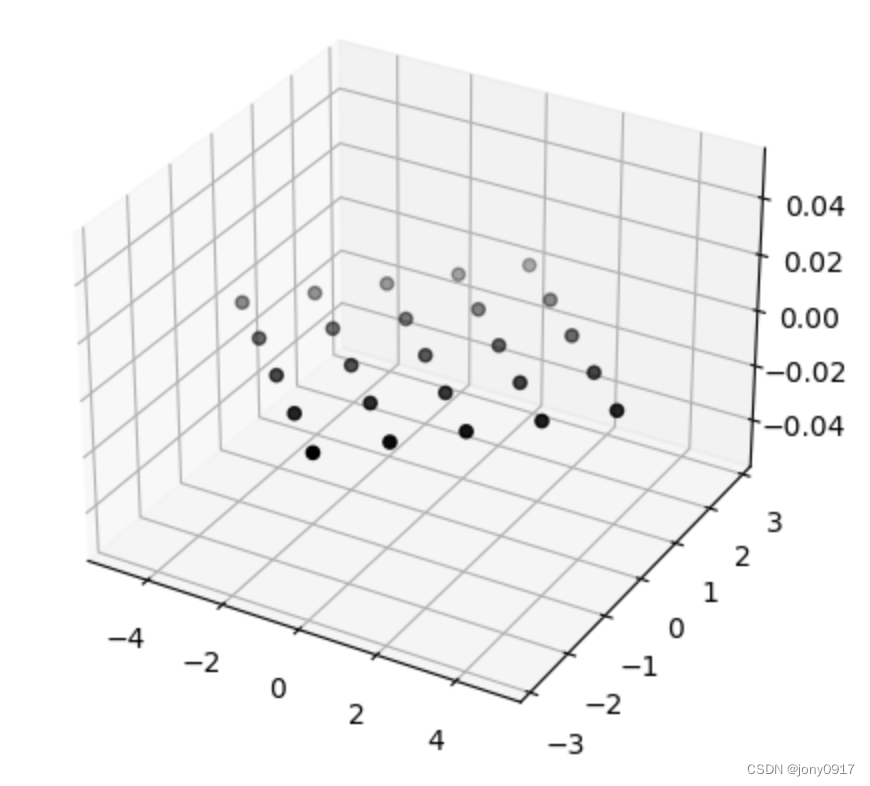 | 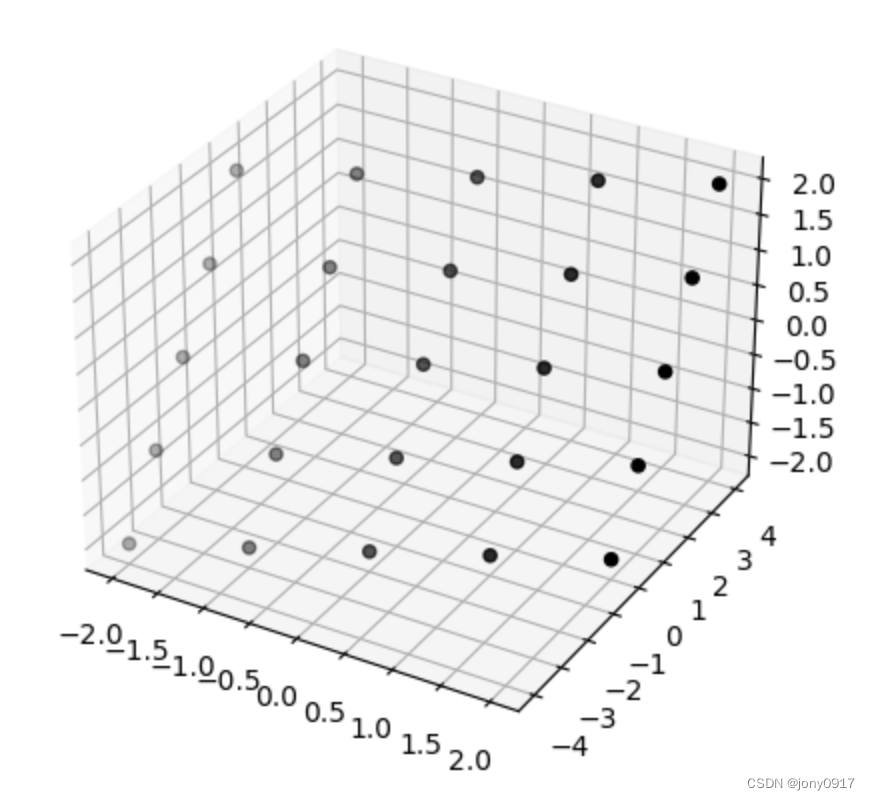 |
相关文章:

图示矩阵分解
特征值与特征向量 设 A A A 是 n 阶矩阵,如果存在数 λ \lambda λ 和 n 维非零列向量 x x x,满足关系式: A x λ x ( 1 ) Ax \lambda x\quad\quad(1) Axλx(1) 则数 λ \lambda λ 称为矩阵 A A A 的特征值,非零向量 x…...
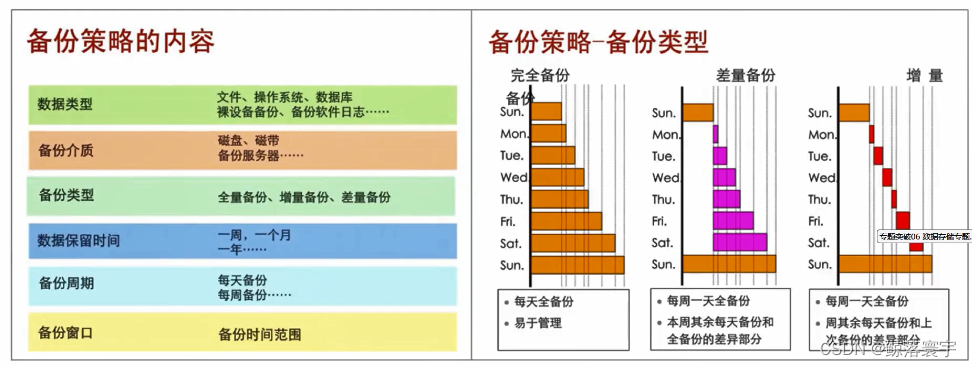
六、互联网技术——数据存储
文章目录 一、存储系统层次结构二、按照重要性分类三、磁盘阵列RAID三、RAID基础四、磁盘阵列分级五、数据备份与恢复六、容灾与灾难恢复 一、存储系统层次结构 常见的三层存储体系结构如下图所示,分为高速缓冲存储器、主存储器和外存储器。 二、按照重要性分类 …...

六、vpp 流表+负载均衡
草稿!!! vpp node其实就是三个部分 1、plugin init 2、set command 3、function 实现功能,比如这里的流表 今天我们再用VPP实现一个流表的功能 一、流表 1.1流表----plugin init VLIB_REGISTER_NODE 注册流表节点 // 注册流…...
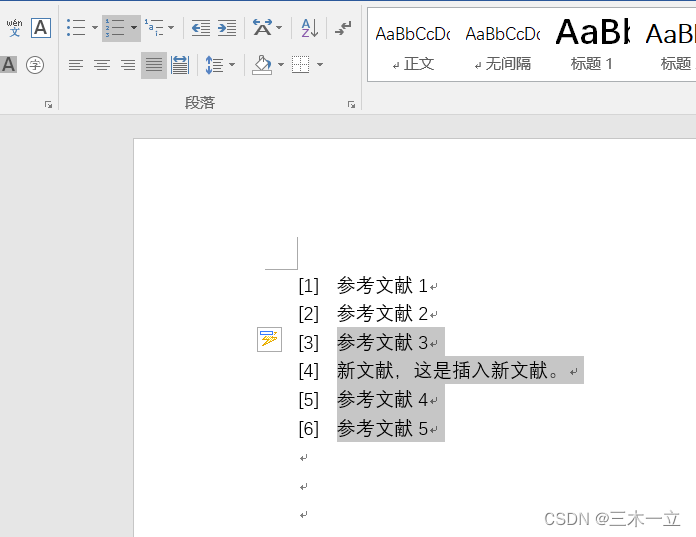
word已排序好的参考文献,插入新的参考文献,序号更新
原排序好的文献序号。 现在在3号后面插入一个新文献。4,5号应该成为5,6 这时在3号后面,回车,就会自动的增长。如下图: 但是如果手滑,把[4]删除了如何排序?? 如下图: …...
二叉树的顺序存储——堆——初识堆排序
前面我们学过可以把完全二叉树存入到顺序表中,然后利用完全二叉树的情缘关系,就可以通过数组下标来联系。 但是并不是把二叉树存入到数组中就是堆了,要看原原来的二叉树是否满足:所有的父都小于等于子,或者所有的父都…...

CYEZ 模拟赛 9
A a ⊥ b ⇒ a − b ⊥ a b (1) a \perp b \Rightarrow a-b \perp ab \tag {1} a⊥b⇒a−b⊥ab(1) 证明: gcd ( a , b ) gcd ( b , a − b ) \gcd(a,b) \gcd(b, a-b) gcd(a,b)gcd(b,a−b),故 a − b ⊥ b a - b \perp b a−b⊥b,同…...
typescript: Builder Pattern
/*** file: CarBuilderts.ts* TypeScript 实体类 Model* Builder Pattern* 生成器是一种创建型设计模式, 使你能够分步骤创建复杂对象。* https://stackoverflow.com/questions/12827266/get-and-set-in-typescript* https://github.com/Microsoft/TypeScript/wiki/…...
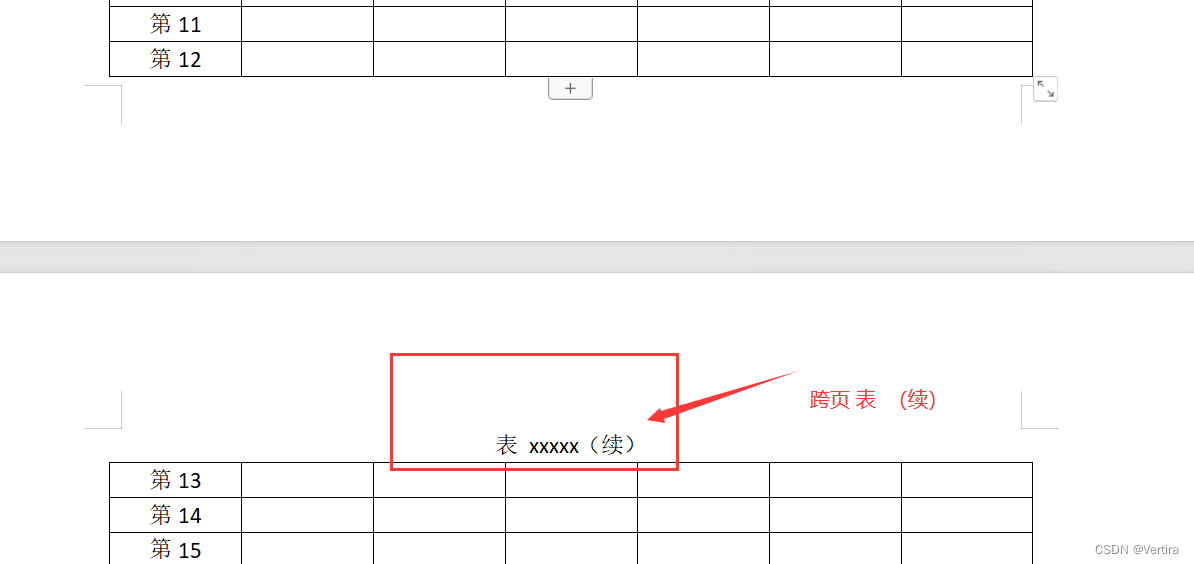
WPS/word 表格跨行如何续表、和表的名称
1:具体操作: 将光标定位在跨页部分的第一行任意位置,按下快捷键ctrlshiftenter,就可以在跨页的表格上方插入空行(在空行可以写,表1-3 xxxx(续)) 在空行中输入…...
Python的NumPy库(一)基础用法
NumPy库并不是Python的标准库,但其在机器学习、大数据等很多领域有非常广泛的应用,NumPy本身就有比较多的内容,全部的学习可能涉及许多的内容,但我们在这里仅学习常见的使用,这些内容对于我们日常使用NumPy是足够的。 …...
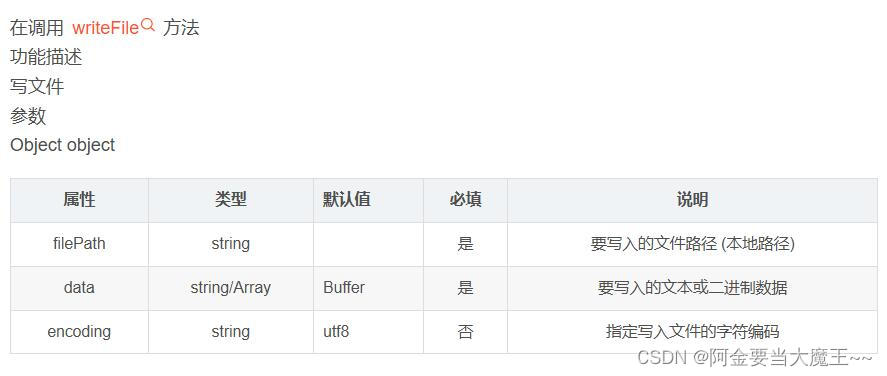
uniapp app 导出excel 表格
直接复制运行 <template><view><button click"tableToExcel">导出一个表来看</button><view>{{ successTip }}</view></view> </template><script>export default {data() {return {successTip: }},metho…...
【RabbitMQ】常用消息模型详解
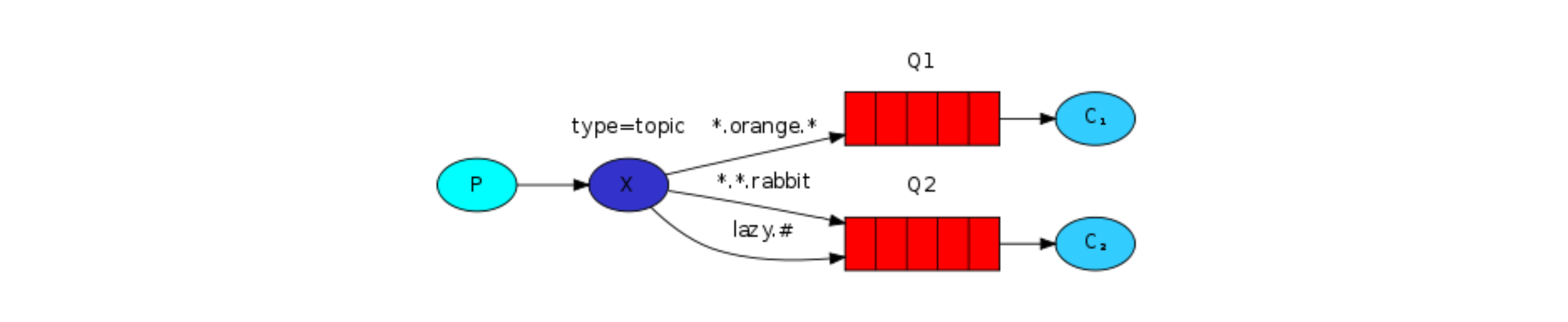
文章目录 AMQP协议的回顾RabbitMQ支持的消息模型第一种模型(直连)开发生产者开发消费者生产者、消费者开发优化API参数细节 第二种模型(work quene)开发生产者开发消费者消息自动确认机制 第三种模型(fanout)开发生产者开发消费者 第四种模型(Routing)开发生产者开发消费者 第五…...

图像拼接后丢失数据,转tiff报错rasterfile failed: an unknown
图像拼接后丢失数据 不仅是数据丢失了,还有个未知原因报错 部分数据存在值不存在的情况 原因 处理遥感数据很容易,磁盘爆满了 解决方案 清理一些无用数据,准备买个2T的外接硬盘用着了。 然后重新做处理...

Nginx之日志模块解读
目录 基本介绍 配置指令 access_log(访问日志) error_log( 错误日志) 基本介绍 Nginx日志主要分为两种:access_log(访问日志)和error_log(错误日志)。Nginx日志主要记录以下信息: 记录Nginx服务启动…...
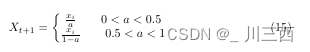
latex方程组编写,一种可以保证方程编号自适应的方法
问题描述: 在利用latex编写方程组时,可以有很多种方法,但不总是编辑好的公式能够显示出编号,故提出一种有效的方程组编写方法 方法: \begin{equation}X_{ t1}\left \{ \begin{matrix}\frac{x_{i}}{a} \quad\quad 0&l…...
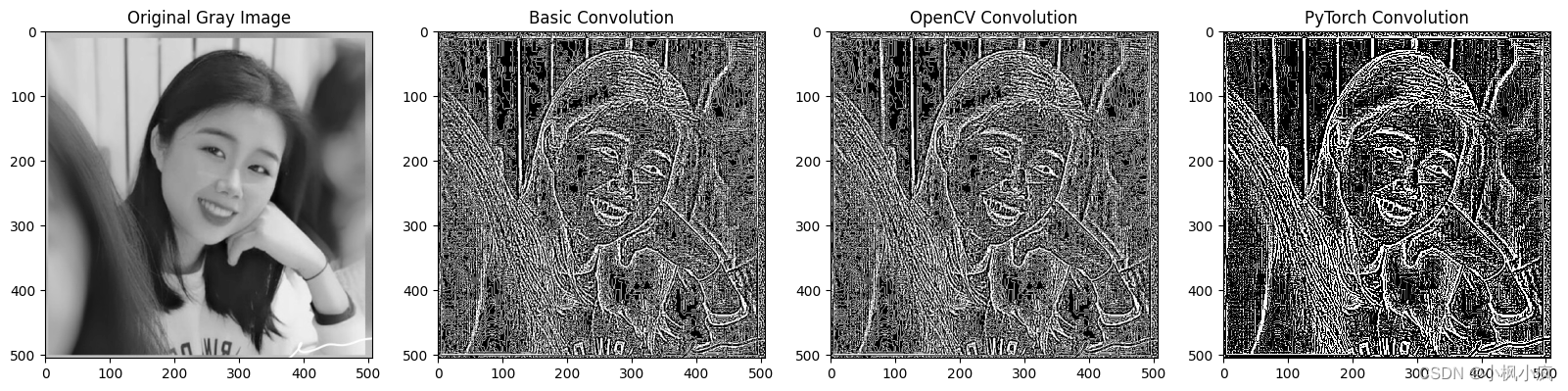
深度学习基础 2D卷积(1)
什么是2D卷积 2D参数量怎么计算 以pytorch为例子,2D卷积在设置的时候具有以下参数,具有输入通道的多少(这个决定了卷积核的通道数量),滤波器数量,这个是有多少个滤波器,越多提取的特征就越有用…...

OpenCV DNN C++ 使用 YOLO 模型推理
OpenCV DNN C 使用 YOLO 模型推理 引言 YOLO(You Only Look Once)是一种流行的目标检测算法,因其速度快和准确度高而被广泛应用。OpenCV 的 DNN(Deep Neural Networks)模块为我们提供了一个简单易用的 API࿰…...
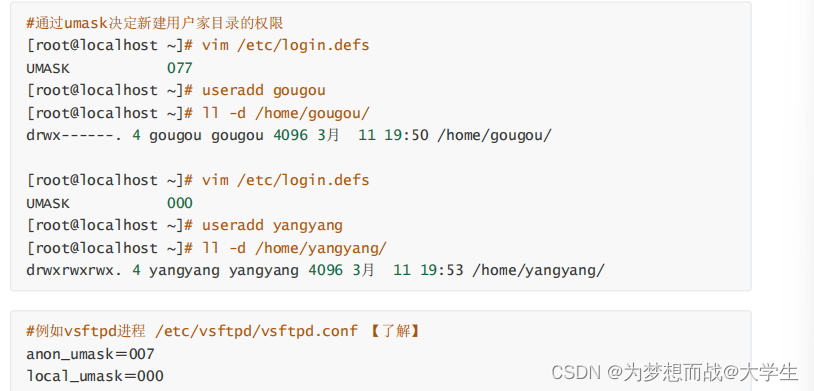
第八章 Linux文件系统权限
目录 8.1 文件的一般权限 1.修改文件或目录的权限---chmod命令 2.对于文件和目录,r,w,x有不同的作用: 3.修改文件或目录的所属主和组---chown,chgrp 8.2 文件和目录的特殊权限 三种通过字符描述文件权限 8.3 ACL 权限 1.A…...
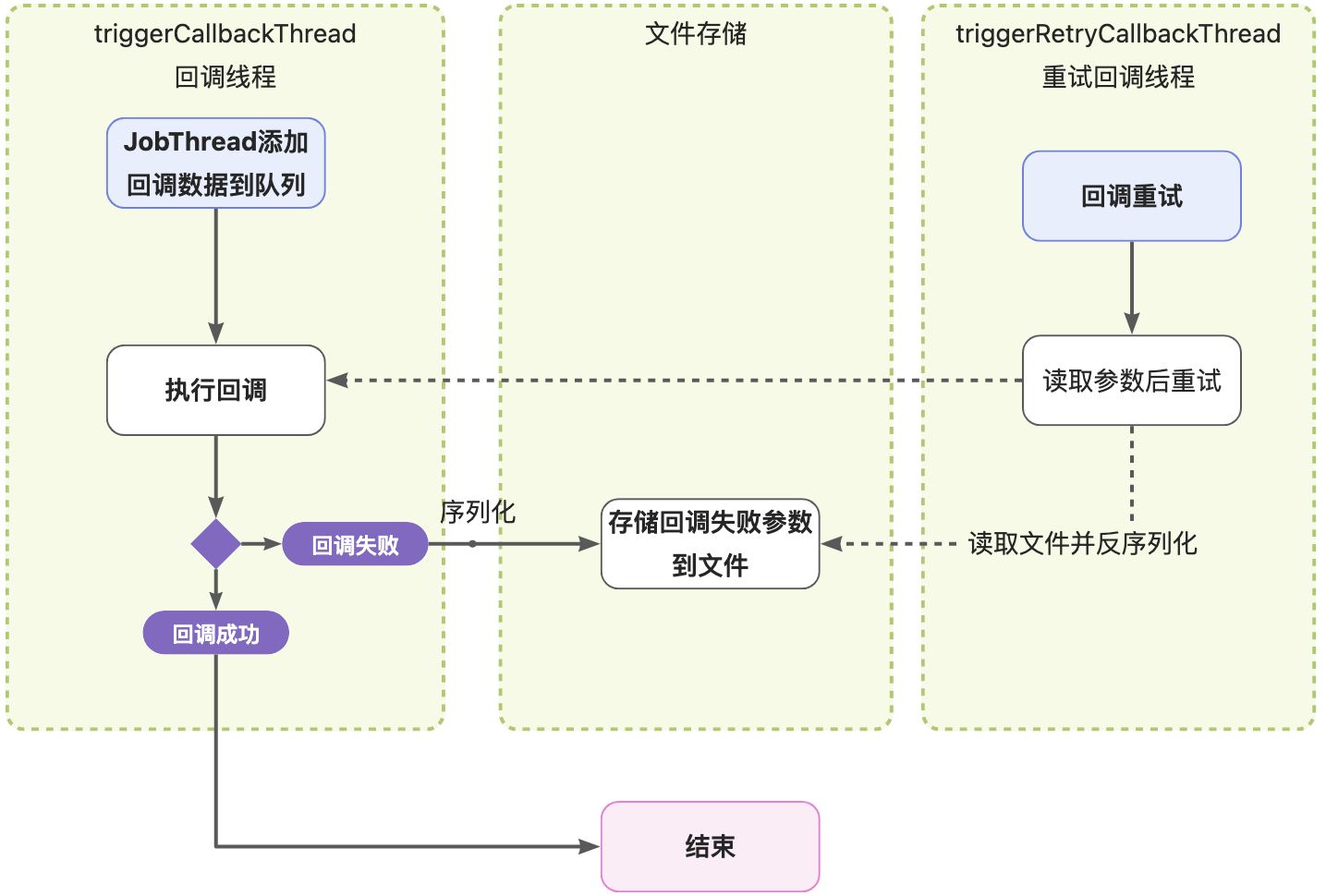
XXL-JOB源码梳理——一文理清XXL-JOB实现方案
分布式定时任务调度系统 流程分析 一个分布式定时任务,需要具备有以下几点功能: 核心功能:定时调度、任务管理、可观测日志高可用:集群、分片、失败处理高性能:分布式锁扩展功能:可视化运维、多语言、任…...
java做个qq机器人
前置的条件 机器人是基于mirai框架实现的。根据官方的文档,建议使用openjdk11。 我这里使用的编辑工具是idea2023 在idea中新建一个maven项目,虽然可以使用gradle进行构建,不过我这里由于网络问题没有跑通。 pom.xml <dependency>&l…...

前端 | AjaxAxios模块
文章目录 1. Ajax1.1 Ajax介绍1.2 Ajax作用1.3 同步异步1.4 原生Ajax 2. Axios2.1 Axios下载2.2 Axios基本使用2.3 Axios方法 1. Ajax 1.1 Ajax介绍 Ajax: 全称(Asynchronous JavaScript And XML),异步的JavaScript和XML。 1.2 Ajax作用 …...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...
