[补题记录] Atcoder Beginner Contest 322(E)
URL:https://atcoder.jp/contests/abc322

目录
E
Probelm/题意
Thought/思路
Code/代码
E
Probelm/题意
有 N 个改进计划,每个计划可以执行一次;有 K 个参数,每个计划可以将所有参数提升固定值,即计划 i 可以为第 j 个参数提升 Aij 的数值。每个计划有花费 Ci,问最少多少花费,能让所有参数都 >= P。
其中 1 <= K, P <= 5;1 <= N <= 100。
Thought/思路
假如只有一个参数,我们很容易想到这是一个 dp。比如:
dp[i][A1] = min(dp[i][A1], dp[i - 1][0 + A1])
dp[i][x] = min(dp[i][x], dp[i - 1][x - A1])
但是现在有 K 个参数,也就是说,我们无法确定 dp 数组的维度。
考虑 K = 5 的情况,就会有 dp[i][A1][A2][A3][A4][A5];再考虑一个参数时,我们是如何得到答案的,显然是通过维护 dp[i][0] ~ dp[i][P] 的最小值来的得到答案 dp[n][P]。
那么我们就可以这样做,将参数 [A1][A2][A3] 视作一系列 P + 1 进制的数(因为需要到达 P),如:[0][0][0] ~ [5][5][5] 就是一系列 3 位的 6 进制数。
这样,就可以将不确定的维度,转换为一维的:dp[i][0 ~ pow(P + 1, K) - 1]。
当我们在状态转移的时候,就可以将十进制的整数,转换为 K 进制数组,对应每个计划的 Aij,算出需要维护的 dp 下一个状态。
Code/代码
#include "bits/stdc++.h"#define int long longconst int inf = 1e15;int n, k, p, dp[107][8003];std::vector <int> tenToK(int x, int k, int bit) { // k 进制std::vector <int> res(bit);for (int i = 0; i < bit; ++ i) {res[i] = x % k;x /= k;}std::reverse(res.begin(), res.end());return res;
}int kToTen(std::vector <int> x, int k, int bit) {int res = 0;for (int i = 0; i < bit; ++ i) {res = res * k + x[i];}return res;
}signed main() {std::cin >> n >> k >> p;int size = (int)std::pow(p + 1, k);for (int i = 0; i <= n; ++ i) {for (int j = 0; j < size; ++ j) {dp[i][j] = inf;}}dp[0][0] = 0;for (int i = 1; i <= n; ++ i) {int c; std::cin >> c;std::vector <int> a(k);for (int j = 0; j < k; ++ j) {std::cin >> a[j];}for (int j = 0; j < size; ++ j) dp[i][j] = dp[i - 1][j]; // 不选 i 的情况for (int j = 0; j < size; ++ j) {std::vector <int> now = tenToK(j, p + 1, k);for (int l = 0; l < k; ++ l) now[l] = std::min(p, now[l] + a[l]);int next = kToTen(now, p + 1, k);dp[i][next] = std::min(dp[i][next], dp[i - 1][j] + c);}}std::cout << (dp[n][size - 1] == inf ? -1 : dp[n][size - 1]);
}相关文章:

[补题记录] Atcoder Beginner Contest 322(E)
URL:https://atcoder.jp/contests/abc322 目录 E Probelm/题意 Thought/思路 Code/代码 E Probelm/题意 有 N 个改进计划,每个计划可以执行一次;有 K 个参数,每个计划可以将所有参数提升固定值,即计划 i 可以为第…...

目标检测算法改进系列之Backbone替换为FocalNet
FocalNet 近些年,Transformers在自然语言处理、图像分类、目标检测和图像分割上均取得了较大的成功,归根结底是自注意力(SA :self-attention)起到了关键性的作用,因此能够支持输入信息的全局交互。但是由于…...
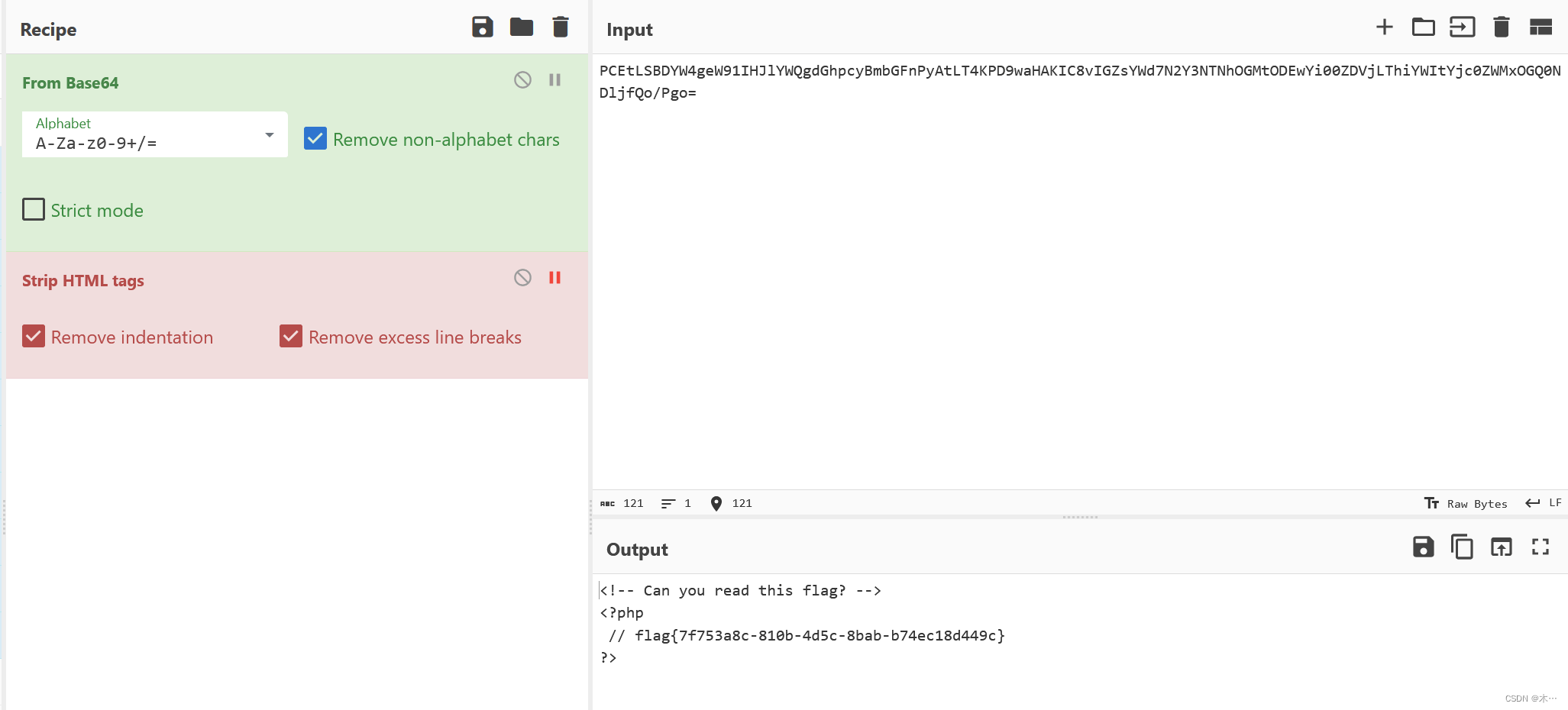
buuctf-[BSidesCF 2020]Had a bad day 文件包含
打开环境 就两个按钮,随便按按 url变了 还有 像文件包含,使用php伪协议读取一下,但是发现报错,而且有两个.php,可能是自己会加上php后缀 所以把后缀去掉 /index.php?categoryphp://filter/convert.base64-encode/resourcei…...
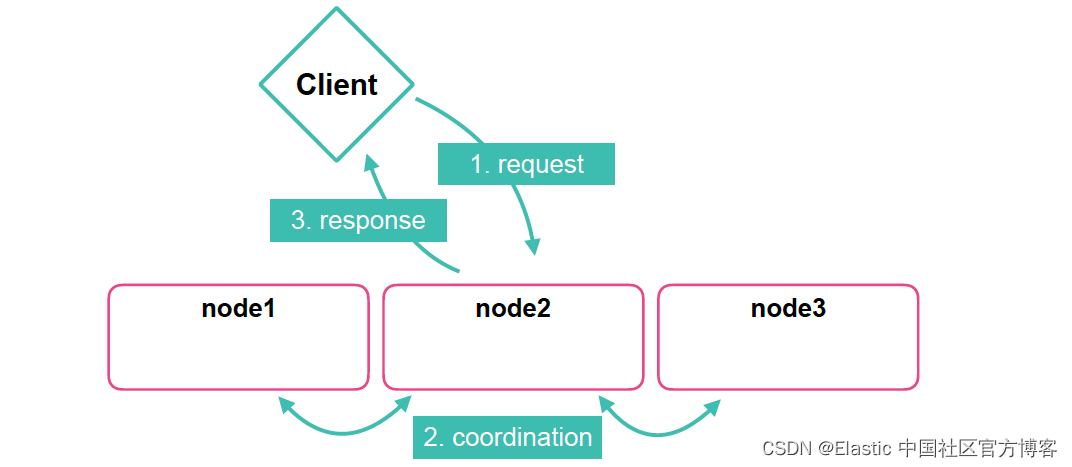
Elasticsearch:什么时候应该考虑在 Elasticsearch 中添加协调节点?
仅协调节点(coordinating only nodes)充当智能负载均衡器。 仅协调节点的这种特殊角色通过减轻数据和主节点的协调责任,为广泛的集群提供了优势。 加入集群后,这些节点与任何其他节点类似,都会获取完整的集群状态&…...
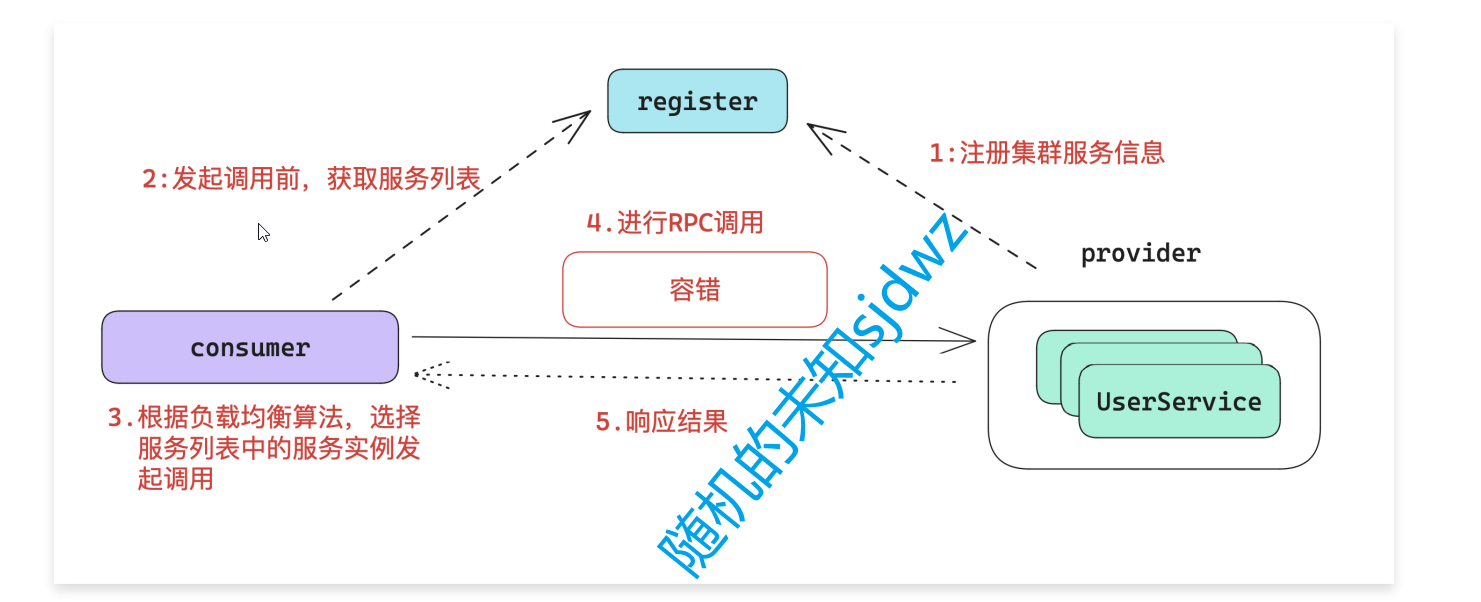
Dubbo3应用开发—Dubbo注册中心引言
Dubbo注册中心引言 什么是Dubbo注册中心 Dubbo的注册中心,是Dubbo服务治理的⼀个重要的概念,他主要用于 RPC服务集群实例的管理。 注册中心的运行流程 使用注册中心的好处 可以有效的管理RPC集群的健康情况,动态的上线或者下线服务。让我…...
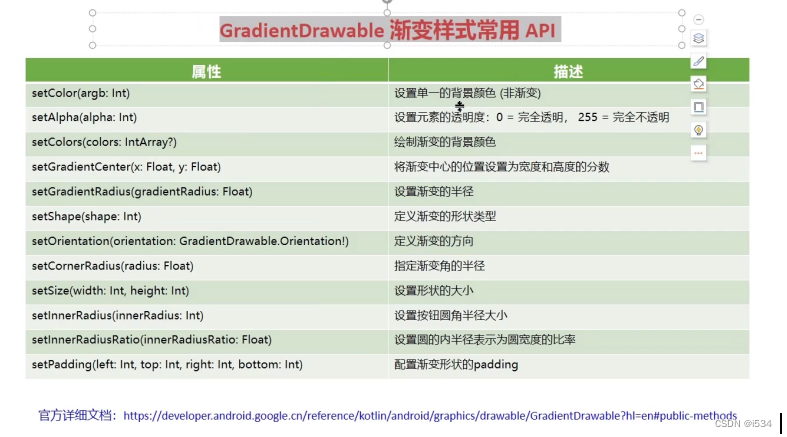
AS环境,版本问题,android开发布局知识
项目模式下有一个build.gradle,每个模块也有自己的build.gradle Android模式下有多个build.gradle,汇总在一起。(都会有标注是哪个模块下的) C:\Users\Administrator\AndroidStudioProjects 项目默认位置 Java web项目与android项目的区别…...
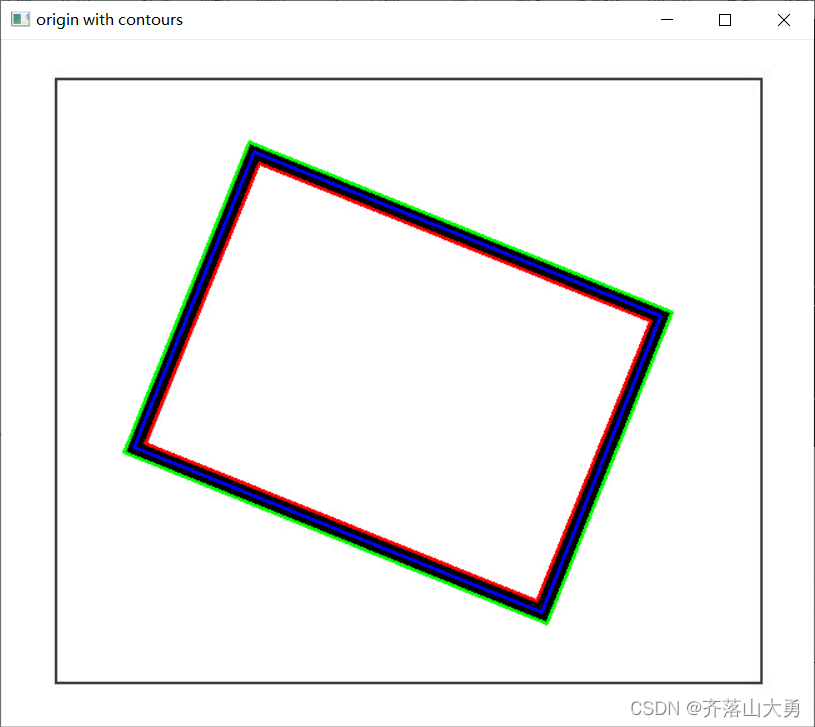
OpenCV查找和绘制轮廓:findContours和drawContours
1 任务描述: 绘制图中粗线矩形的2个边界,并找到其边界的中心线 图1 原始图像 2.函数原型 findContours( InputOutputArray image, OutputArrayOfArrays contours, OutputArray hierarchy, int mode, …...
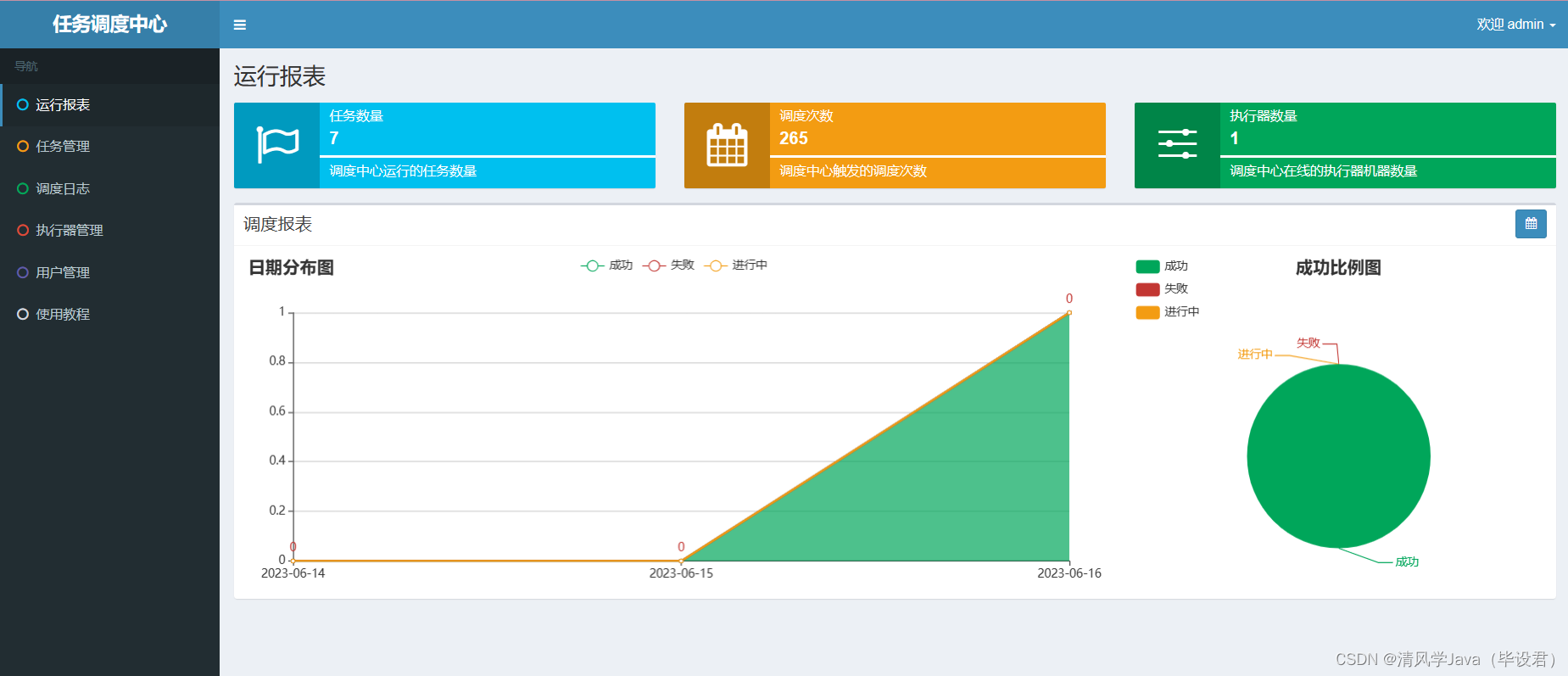
毕设-原创医疗预约挂号平台分享
医疗预约挂号平台 不是尚医通项目,先看项目质量(有源码论文) 项目链接:医疗预约挂号平台git地址 演示视频:医疗预约挂号平台 功能结构图 登录注册模块:该模块具体分为登录和注册两个功能,这些…...
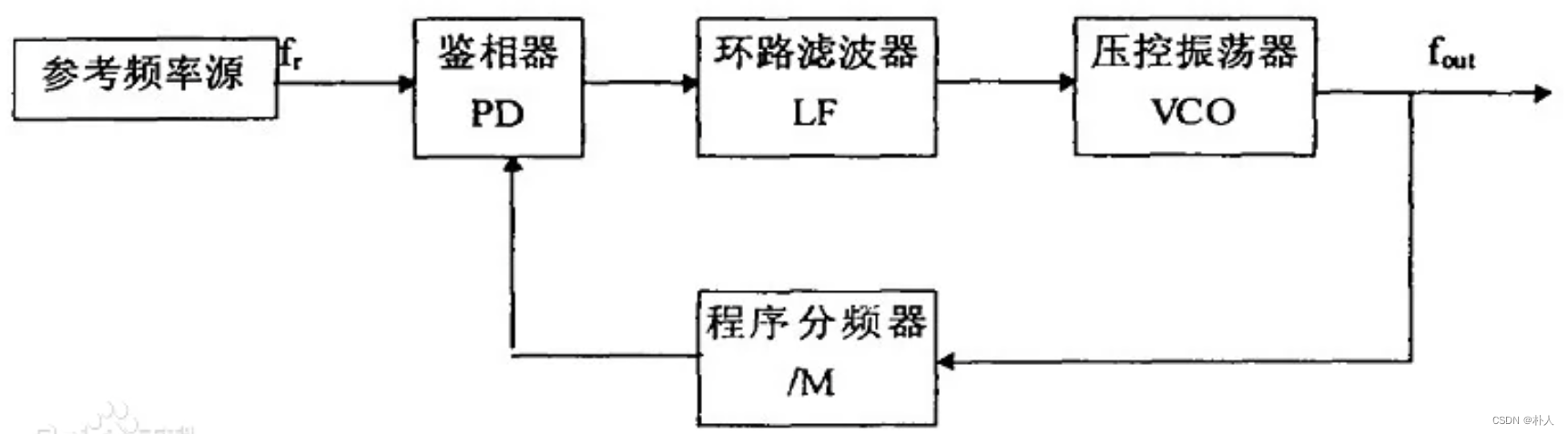
PLL锁相环倍频原理
晶振8MHz,但是处理器输入可以达到72MHz,是因为PLL锁相环提供了72MHz。 锁相环由PD(鉴相器)、LP(滤波器)、VCO(压控振荡器)组成。 处理器获得的72MHz并非晶振提供,而是锁…...
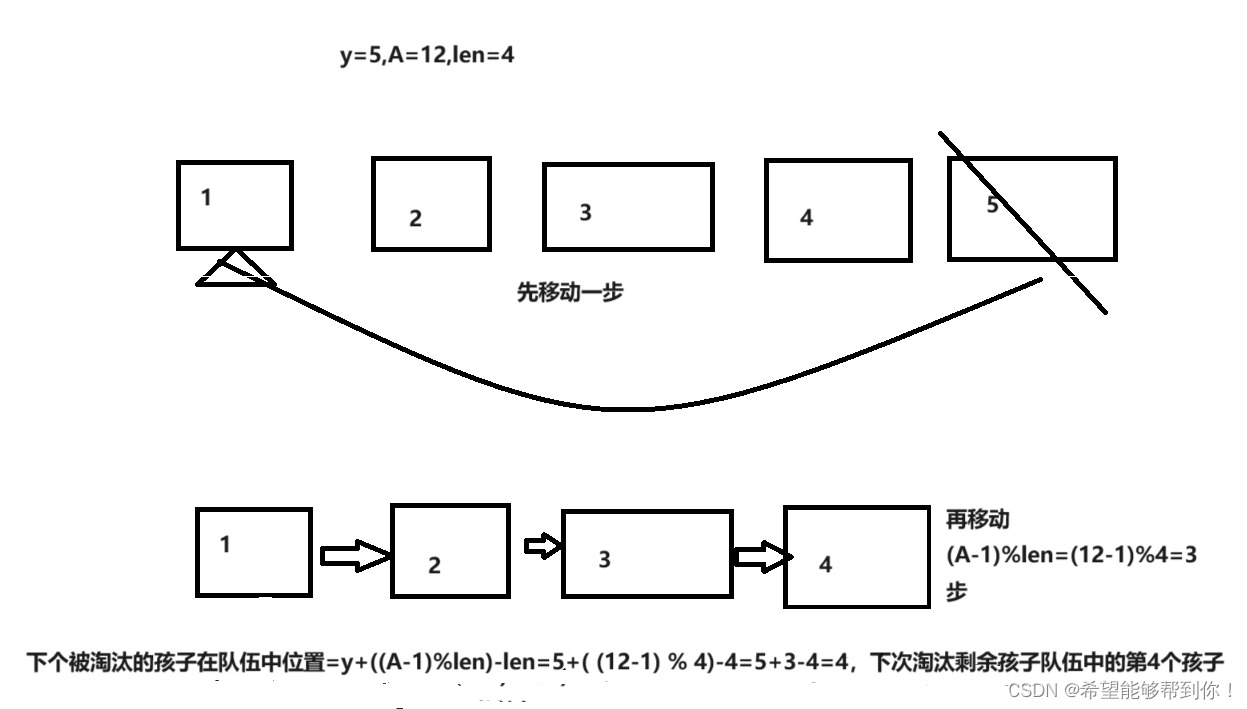
POJ 2886 Who Gets the Most Candies? 树状数组+二分
一、题目大意 我们有N个孩子,每个人带着一张卡片,一起顺时针围成一个圈来玩游戏,第一回合时,第k个孩子被淘汰,然后他说出他卡片上的数字A,如果A是一个正数,那么下一个回合他左边的第A个孩子被淘…...

阿里云服务器镜像系统Anolis OS龙蜥详细介绍
阿里云服务器Anolis OS镜像系统由龙蜥OpenAnolis社区推出,Anolis OS是CentOS 8 100%兼容替代版本,Anolis OS是完全开源、中立、开放的Linux发行版,具备企业级的稳定性、高性能、安全性和可靠性。目前阿里云服务器ECS可选的Anolis OS镜像系统版…...

数学建模Matlab之基础操作
作者由于后续课程也要学习Matlab,并且之前也进行了一些数学建模的练习(虽然是论文手),所以花了几天零碎时间学习Matlab的基础操作,特此整理。 基本运算 a55 %加法,同理减法 b2^3 %立方 c5*2 %乘法 x 1; …...
[计算机入门] Windows附件程序介绍(工具类)
3.14 Windows附件程序介绍(工具类) 3.14.1 计算器 Windows系统中的计算器是一个内置的应用程序,提供了基本的数学计算功能。它被设计为一个方便、易于使用的工具,可以满足用户日常生活和工作中的基本计算需求。 以下是计算器程序的主要功能:…...

队列(循环数组队列,用队列实现栈,用栈实现队列)
基础知识 队列(Queue):先进先出的数据结果,底层由双向链表实现 入队列:进行插入操作的一端称为队尾出队列:进行删除操作的一端称为对头 常用方法 boolean offer(E e) 入队 E(弹出元素的类型) poll() 出队 peek() 获取队头 int size 获取队列元素个数 boolean isEmpty(…...
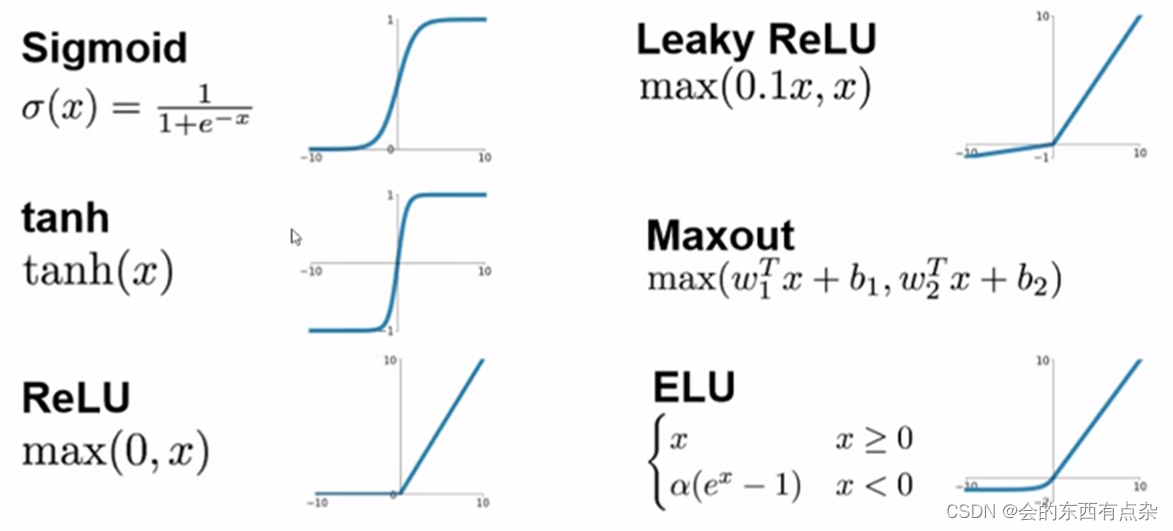
卷积神经网络-池化层和激活层
2.池化层 根据特征图上的局部统计信息进行下采样,在保留有用信息的同时减少特征图的大小。和卷积层不同的是,池化层不包含需要学习的参数。最大池化(max-pooling)在一个局部区域选最大值作为输出,而平均池化(average pooling)计算一个局部区…...
API基础————包
什么是包,package实际上就是一个文件夹,便于程序员更好的管理维护自己的代码。它可以使得一个项目结构更加清晰明了。 Java也有20年历史了,这么多年有这么多程序员写了无数行代码,其中有大量重复的,为了更加便捷省时地…...

【C++】一文带你走入vector
文章目录 一、vector的介绍二、vector的常用接口说明2.1 vector的使用2.2 vector iterator的使用2.3 vector空间增长问题2.4 vector 增删查改 三、总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价ヾ(๑╹◡╹)ノ" 一、vector的介绍 vector…...
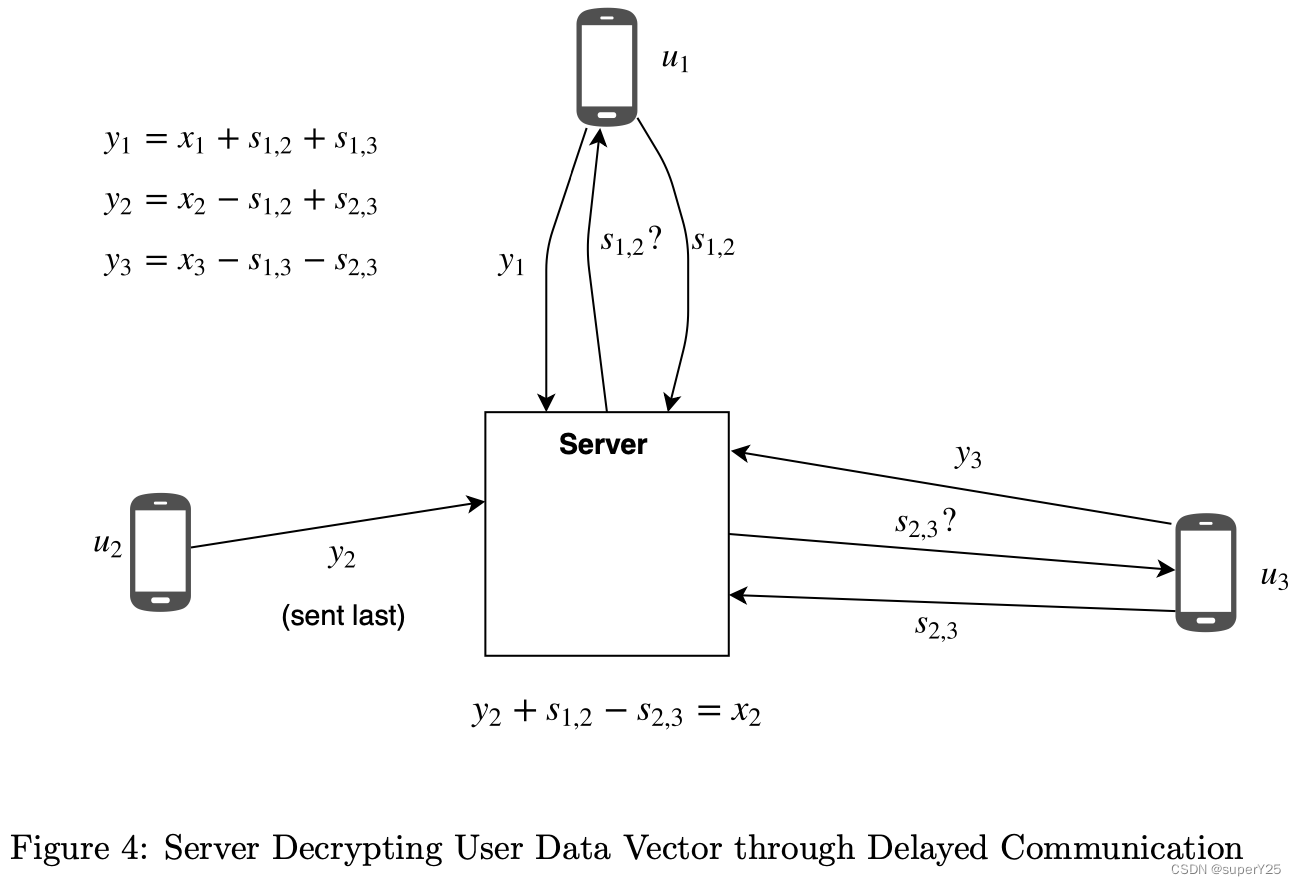
《Secure Analytics-Federated Learning and Secure Aggregation》论文阅读
背景 机器学习模型对数据的分析具有很大的优势,很多敏感数据分布在用户各自的终端。若大规模收集用户的敏感数据具有泄露的风险。 对于安全分析的一般背景就是认为有n方有敏感数据,并且不愿意分享他们的数据,但可以分享聚合计算后的结果。 联…...
十三、Django之添加用户(原始方法实现)
修改urls.py path("user/add/", views.user_add),添加user_add.html {% extends layout.html %} {% block content %}<div class"container"><div class"panel panel-default"><div class"panel-heading"><h3 c…...

Elasticsearch数据操作原理
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
