POJ 2886 Who Gets the Most Candies? 树状数组+二分
一、题目大意
我们有N个孩子,每个人带着一张卡片,一起顺时针围成一个圈来玩游戏,第一回合时,第k个孩子被淘汰,然后他说出他卡片上的数字A,如果A是一个正数,那么下一个回合他左边的第A个孩子被淘汰,如果A是一个负数,那么下一个回合,他右边的第(-A)个孩子被淘汰,如下图所示,即A>0,向着下标增大的方向,A<0,向着下标减小的方向。
 其中,第 i (1<=i<=N)回合被淘汰的孩子,可以得到F(i)颗糖果,F(i)代表可以整除 i 的因子的数量(包括1和它本身),最终需要输出 N 个孩子中,得到最多的孩子的名字和他得到的糖果数量,假如说有多个孩子都得到这个糖果数量,输出那个最先被淘汰的。
其中,第 i (1<=i<=N)回合被淘汰的孩子,可以得到F(i)颗糖果,F(i)代表可以整除 i 的因子的数量(包括1和它本身),最终需要输出 N 个孩子中,得到最多的孩子的名字和他得到的糖果数量,假如说有多个孩子都得到这个糖果数量,输出那个最先被淘汰的。
二、解题思路
首先看这个F(i)代表整除 i 的数量,然后针对输入的 N,我们要找出其中使得 F(i)最大的i,同时如果有多个 i 的F(i)一样,取那个最小的 i。
我们可以定义一个数组F[i],对于某一个数字 i,只需要枚举 [1,根号i取整] 范围内的数字 j ,然后如果 i % j == 0,F[i]+=2(因为 j 和 i / j 都是整除 i 的因子,所以需要都加上)然后若 j == i / j ,那么F[i]+=1即可,因为两个乘数相等了。
然后我们根据输入的 N,要迅速找到其中 i ∈[1,N]且 F[i]最大的i,那么考虑可先打表,计算好F[i]数组之后,从1到500000循环,定义一个数组optF,其中optF[i]代表 j∈[1,i]时,使得 f[j]最大的j。给optF[0]=0,然后1<=i<=500000循环,如果F[i]>optF[i-1],则optF[i]=i,否则optF[i]=optF[i-1],这样可以达到两点,1、对于给定的N,直接用optF[N]可以迅速定位到 j ∈ [1,N],使F[j]最大的j。2、当F[p]==F[p+k]时,因为时从1循环,以大于为条件,所以当 p <=N且 p+k<=N时,我们会找到满足条件的顺序最靠前的p。
举个例子吧,
1、N∈[1,1]时,最大的因子数是1,N以内最优的数字也是1;
2、N∈[2,3]时,最大的因子数是2,N以内最优的数字是2;
3、N∈[4,5]时,最大的因子数是3,N以内最优的数字是4;
4、N∈[6,11]时,最大的因子数是4,N以内最优的数字是6;
4、N∈[12,23]时,最大的因子数是6,N以内最优的数字是12;
那么来分析下复杂性,计算F数组的值需要的时间复杂性是 O ( N * 根号N),根据F数组,计算optF数组的复杂性是O(N),对于500000的数据量, O ( N * 根号N)太慢了。那么我们考虑下,hi发现针对 N<=23时,我们只需要记录4个区间的边界和最优的那个F[i]即可。那么对于500000个数字呢?我试了下发现只有35个区间,于是果断写程序把这35个区间的右边界、左边界和最优数字的因子数的打出来的,打表的程序如下。(我发现每次的左边界就是最优数字)
#include <iostream>
using namespace std;
typedef pair<int, int> P;
P tbl[500009];
int f[500009], optF[500009], len;
void initF()
{f[0] = 0;for (int i = 1; i <= 500000; i++){f[i] = 0;for (int j = 1; j * j <= i; j++){if (i % j == 0){f[i] = f[i] + 2;if (j * j == i){f[i] = f[i] - 1;}}}}
}
void initOptF()
{optF[0] = 0;for (int i = 1; i <= 500000; i++){if (f[i] > f[optF[i - 1]]){optF[i] = i;}else{optF[i] = optF[i - 1];}}
}
void printTbl()
{len = 1;tbl[1] = P(1, optF[1]);for (int i = 2; i <= 500000; i++){if (tbl[len].second == optF[i] && i > tbl[len].first){tbl[len].first = i;}else if (tbl[len].second != optF[i]){tbl[++len] = P(i, optF[i]);}}for (int i = 1; i <= len; i++){printf("%d %d %d\n", tbl[i].first, tbl[i].second, f[tbl[i].second]);}printf("%d\n", len);
}
int main()
{initF();initOptF();printTbl();return 0;
}这样的话,根据任意的N,找出 i ∈[1,N],且F[i]最大的 i(存在F[i]和F[i+k]相同时,自动定到F[i]),同时算出F[i]的值,可以直接根据这张表在O(1)时间内完成。
int n_Tbl[] = {1, 3, 5, 11, 23, 35, 47, 59, 119, 179, 239, 359, 719, 839, 1259, 1679, 2519, 5039, 7559, 10079, 15119, 20159, 25199, 27719, 45359, 50399, 55439, 83159, 110879, 166319, 221759, 277199, 332639, 498959, 500000};
int k_Tbl[] = {1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, 15120, 20160, 25200, 27720, 45360, 50400, 55440, 83160, 110880, 166320, 221760, 277200, 332640, 498960};
int f_Tbl[] = {1, 2, 3, 4, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 32, 36, 40, 48, 60, 64, 72, 80, 84, 90, 96, 100, 108, 120, 128, 144, 160, 168, 180, 192, 200};假设,根据N我们找到那个最优数字是optOrder,然后接下来需要考虑的就是,如何找到第 optOrder 个被淘汰的孩子呢?
我的思路是模拟出整个游戏的过程,维护一个树状数组,起初的时候给[1,N]内所有的元素的位置都+1,然后每当第x位置的孩子淘汰的时候,给树状数组update(x,-1)。
使用树状数组+二分查找可以迅速找到当前没有被淘汰的孩子中的第 q 个q∈[1,len],len为当前内有被淘汰的孩子数量,
1、 L = 0 ,R = n+1
2、mid=(L+R)/2
3、query(mid)(树状数组[1,mid]的和)小于q时,L=mid,否则R=mid
4、L+1>=R时,返回 L+1,L+1就是当前未被淘汰的第q个孩子的下标。
那么来考虑这个游戏的过程,一开始的时候第k个孩子被淘汰,然后根据他卡片上的数字 A 判断下一个孩子,卡片上的数字一定不为0。这里我把这个移动分为两步:
1、先在A方向上移动一步到一个当前没有被淘汰的点
2、然后再移动 A - 1步
然后第二步骤移动时,其实是一个关于当前剩余数量的周期运动,如下图所示。
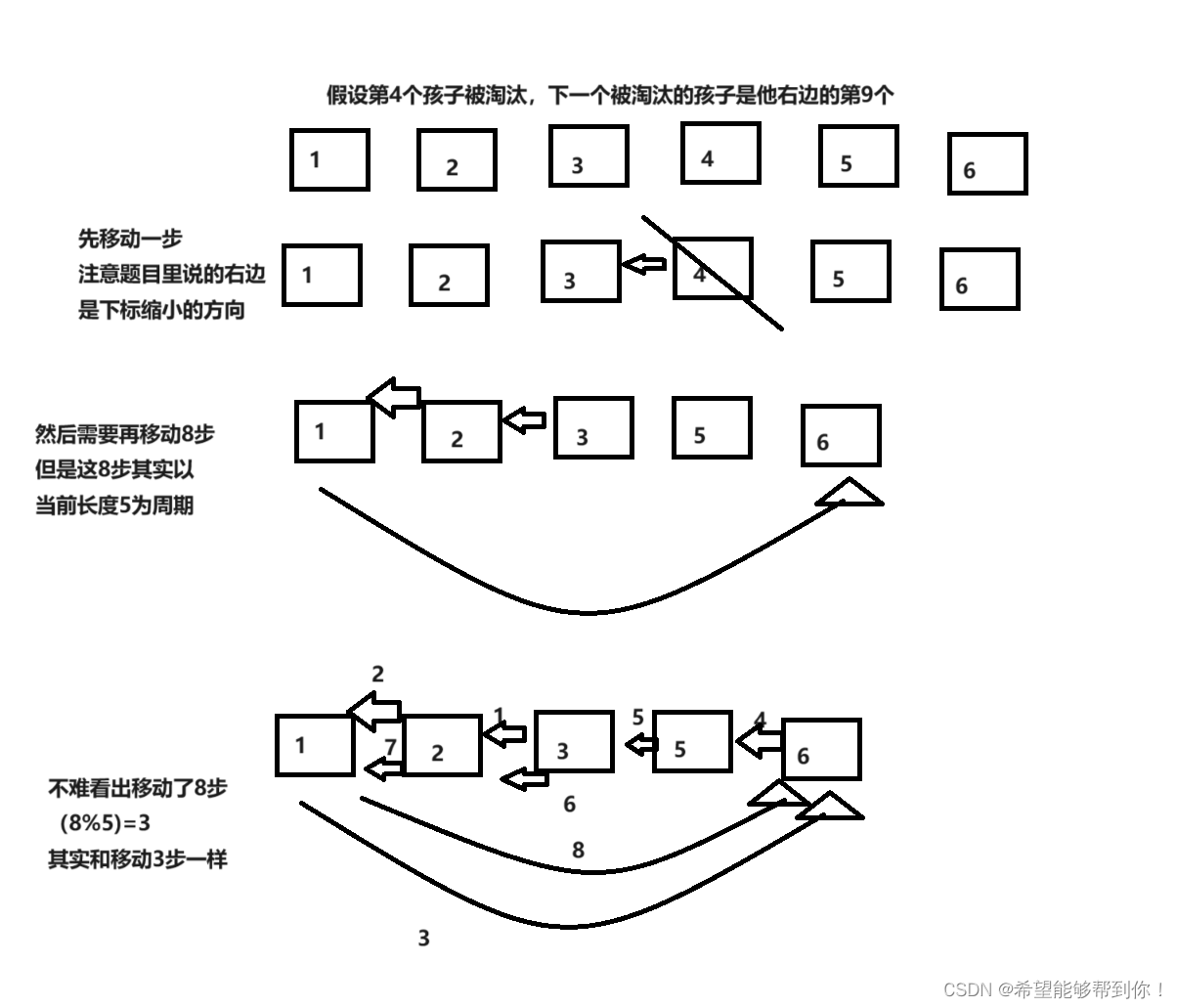
所以我们把可以把移动的过程优化一下,假设第x个孩子被淘汰,第x个孩子的卡片上数字是A,第x个孩子被淘汰以后,剩余孩子的数量是len
1、先在A方向上移动一步到一个当前没有被淘汰的点
2、然后再移动 (A - 1)% len 步
然后这样的话,就变得简单许多了,我们先利用树状前[1,x]项的和找到下标 x 在被淘汰前在孩子们中的顺序y,之后update(x,-1)代表x被淘汰,同时记录剩余孩子的数量为len,
假设是A是朝着数组下标缩小的方向(题目中的右)
记录方向之后,把A变成正数,便于计算。
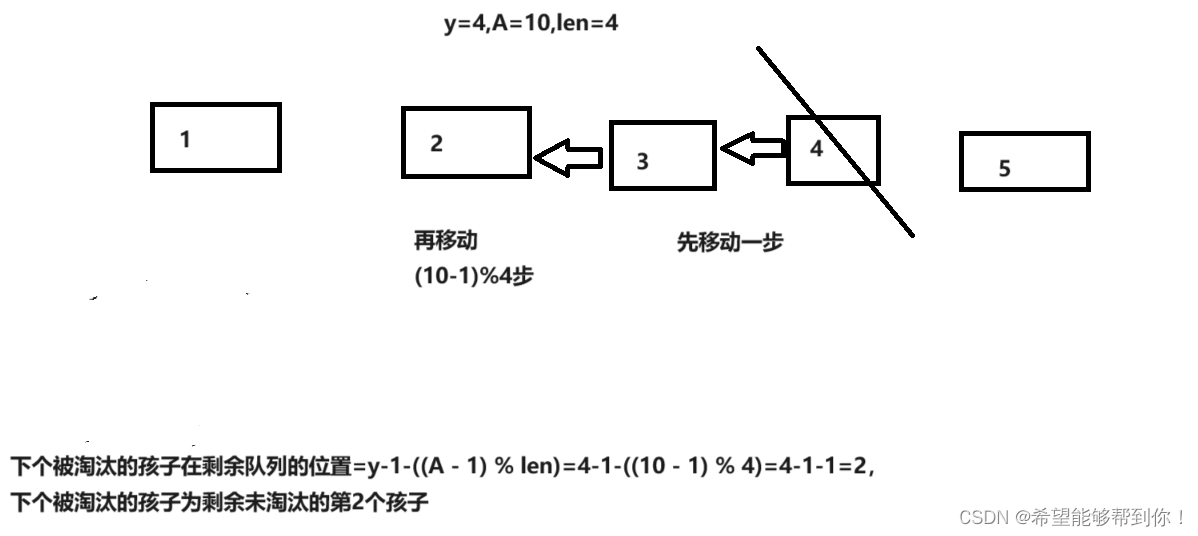
1、被淘汰的孩子位置在y,先挪一步,到 y-1,判断y-1是否大于 (A-1)%len ,如果是,那么下一个被淘汰孩子就是 y - 1 - ((A-1)%len),如下图所示。
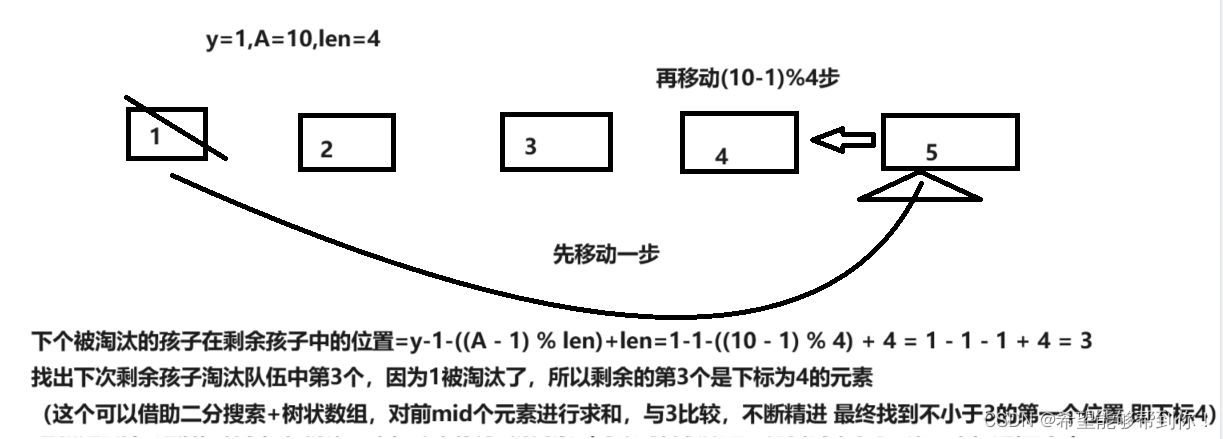
2、如果y-1小于等于 (A-1)%len,那么下一个被淘汰的孩子就是 y - 1 - ((A-1)%len) + len,我给出了2个案例,如下两张图所示。

这样就将A向着数组下标缩小方向的所有情况都考虑到了
接下来继续考虑A向着数组下标放大的方向(题目中的左,实际其实是右)
依旧设本次被淘汰的元素在被淘汰前的位置作为y,淘汰掉y之后剩余孩子的数量为len,y手里的数字为A。
1、首先考虑y加上(A-1)%len小于等于len的情况,这种情况下,下一个被淘汰的位置为 y + ((A-1)%len),如下图

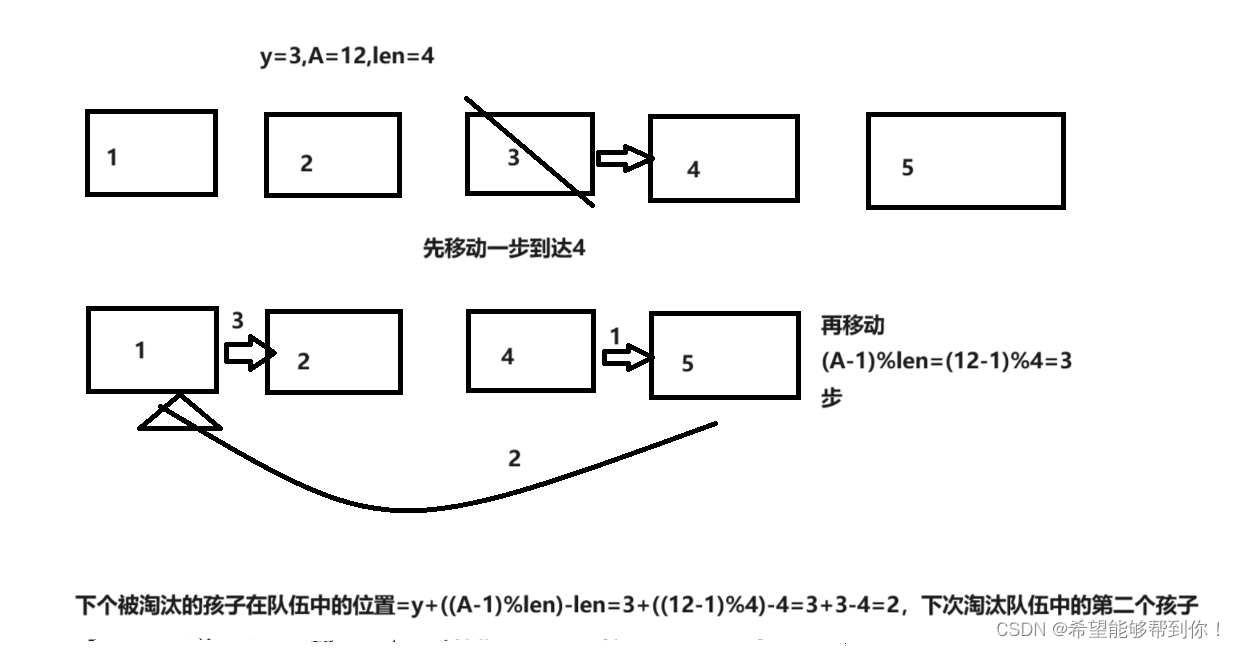
2、接下来,再来考虑y加上(A-1)%len大于len的情况,这种情况下,可以画图看出下一个被淘汰的位置为y+((A-1)%len) - len,我给出了两个案例,如下两张图所示。
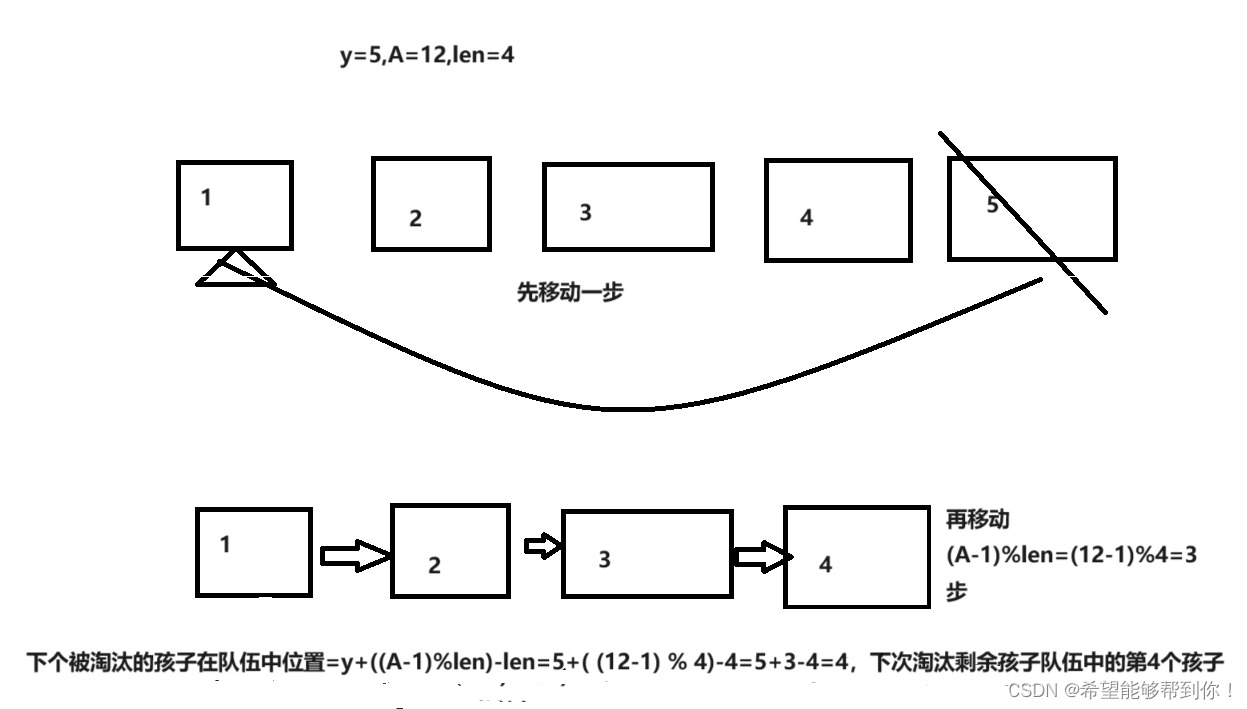
这样就把所有的4种情况考虑完了,知道当前被淘汰的元素下标k后,可知A,也可以通过树状数组计算出它在队伍中的位置y,然后更新树状数组k的位置为-1,剩余长度len自减1,之后通过位置y、偏移A、队伍长度len和上文中的4个if,求出下个被淘汰的孩子在队伍中的位置,然后根据位置对树状数组进行二分,求出下标,更新k为这个下标,继续下一次的循环,这样循环n次,第 i 循环开始时对应的k,就是第i个被淘汰的孩子,这样就可以知道每个孩子被淘汰的顺序了。
之后输出上文中 第optOrder个被淘汰的孩子的名字,和optOrder对应的F值即可。
总结下吧,像这种情况比较多的问题,最好是画下图,我们不需要背下这4个if,只需要能够记得是4种,然后画个图,一个一个找出来就可以
三、代码
#include <iostream>
using namespace std;
int n_Tbl[] = {1, 3, 5, 11, 23, 35, 47, 59, 119, 179, 239, 359, 719, 839, 1259, 1679, 2519, 5039, 7559, 10079, 15119, 20159, 25199, 27719, 45359, 50399, 55439, 83159, 110879, 166319, 221759, 277199, 332639, 498959, 500000};
int k_Tbl[] = {1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, 15120, 20160, 25200, 27720, 45360, 50400, 55440, 83160, 110880, 166320, 221760, 277200, 332640, 498960};
int f_Tbl[] = {1, 2, 3, 4, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 32, 36, 40, 48, 60, 64, 72, 80, 84, 90, 96, 100, 108, 120, 128, 144, 160, 168, 180, 192, 200};
int n_, n, bit[524298], card[500009], order[500009], k;
char name[500009][50];
int optFOrder()
{for (int i = 0; i < 35; i++){if (n_ <= n_Tbl[i]){return k_Tbl[i];}}return -1;
}
int f(int num)
{for (int i = 0; i < 35; i++){if (num <= n_Tbl[i]){return f_Tbl[i];}}return -1;
}
void input()
{for (int i = 1; i <= n_; i++){scanf("\n%s %d", &name[i], &card[i]);}
}
void init()
{n = 1;while (n < n_){n = n * 2;}for (int i = 0; i <= n; i++){bit[i] = 0;}
}
void update(int r, int v)
{if (r <= 0){return;}for (int i = r; i <= n; i = i + (i & (-i))){bit[i] = bit[i] + v;}
}
int query(int r)
{int sum = 0;for (int i = r; i > 0; i = i - (i & (-i))){sum = sum + bit[i];}return sum;
}
void push()
{for (int i = 1; i <= n_; i++){update(i, 1);}
}
int binarySearch(int num)
{int l = 0, r = n + 1;while (l + 1 < r){int mid = (l + r) / 2;if (query(mid) < num){l = mid;}else{r = mid;}}return (l + 1);
}
int absVal(int num)
{if (num < 0){return num * (-1);}else{return num;}
}
void solve()
{int len = n_;for (int i = 1; i <= n_; i++){order[i] = k;if (i == n_){break;}len--;int currentOrder = query(k);update(k, -1);bool left = (card[k] < 0);card[k] = absVal(card[k]);// 默认先挪动一步,挪动一步之后就是len下的周期运动card[k]--;card[k] = card[k] % len;if (left && ((currentOrder - 1) > card[k])){k = currentOrder - 1 - card[k];}else if (left && ((currentOrder - 1) <= card[k])){k = currentOrder - 1 - card[k] + len;}else if (!left && (currentOrder + card[k]) <= len){k = currentOrder + card[k];}else if (!left && (currentOrder + card[k]) > len){k = currentOrder + card[k] - len;}k = binarySearch(k);}
}
int main()
{while (~scanf("%d%d", &n_, &k)){input();init();push();solve();printf("%s %d\n", name[order[optFOrder()]], f(n_));}return 0;
}相关文章:

POJ 2886 Who Gets the Most Candies? 树状数组+二分
一、题目大意 我们有N个孩子,每个人带着一张卡片,一起顺时针围成一个圈来玩游戏,第一回合时,第k个孩子被淘汰,然后他说出他卡片上的数字A,如果A是一个正数,那么下一个回合他左边的第A个孩子被淘…...

阿里云服务器镜像系统Anolis OS龙蜥详细介绍
阿里云服务器Anolis OS镜像系统由龙蜥OpenAnolis社区推出,Anolis OS是CentOS 8 100%兼容替代版本,Anolis OS是完全开源、中立、开放的Linux发行版,具备企业级的稳定性、高性能、安全性和可靠性。目前阿里云服务器ECS可选的Anolis OS镜像系统版…...

数学建模Matlab之基础操作
作者由于后续课程也要学习Matlab,并且之前也进行了一些数学建模的练习(虽然是论文手),所以花了几天零碎时间学习Matlab的基础操作,特此整理。 基本运算 a55 %加法,同理减法 b2^3 %立方 c5*2 %乘法 x 1; …...
[计算机入门] Windows附件程序介绍(工具类)
3.14 Windows附件程序介绍(工具类) 3.14.1 计算器 Windows系统中的计算器是一个内置的应用程序,提供了基本的数学计算功能。它被设计为一个方便、易于使用的工具,可以满足用户日常生活和工作中的基本计算需求。 以下是计算器程序的主要功能:…...

队列(循环数组队列,用队列实现栈,用栈实现队列)
基础知识 队列(Queue):先进先出的数据结果,底层由双向链表实现 入队列:进行插入操作的一端称为队尾出队列:进行删除操作的一端称为对头 常用方法 boolean offer(E e) 入队 E(弹出元素的类型) poll() 出队 peek() 获取队头 int size 获取队列元素个数 boolean isEmpty(…...
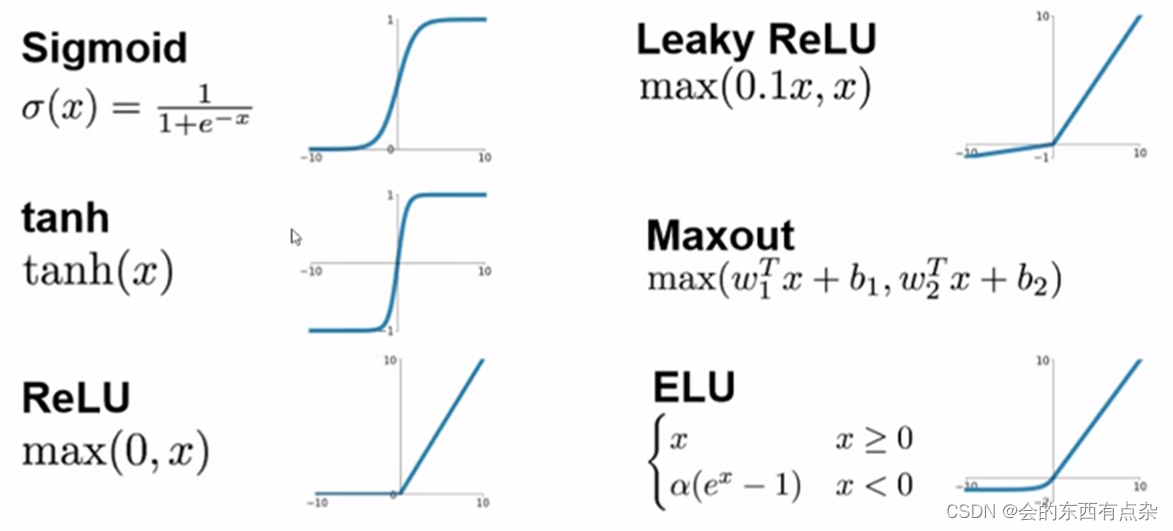
卷积神经网络-池化层和激活层
2.池化层 根据特征图上的局部统计信息进行下采样,在保留有用信息的同时减少特征图的大小。和卷积层不同的是,池化层不包含需要学习的参数。最大池化(max-pooling)在一个局部区域选最大值作为输出,而平均池化(average pooling)计算一个局部区…...
API基础————包
什么是包,package实际上就是一个文件夹,便于程序员更好的管理维护自己的代码。它可以使得一个项目结构更加清晰明了。 Java也有20年历史了,这么多年有这么多程序员写了无数行代码,其中有大量重复的,为了更加便捷省时地…...

【C++】一文带你走入vector
文章目录 一、vector的介绍二、vector的常用接口说明2.1 vector的使用2.2 vector iterator的使用2.3 vector空间增长问题2.4 vector 增删查改 三、总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价ヾ(๑╹◡╹)ノ" 一、vector的介绍 vector…...
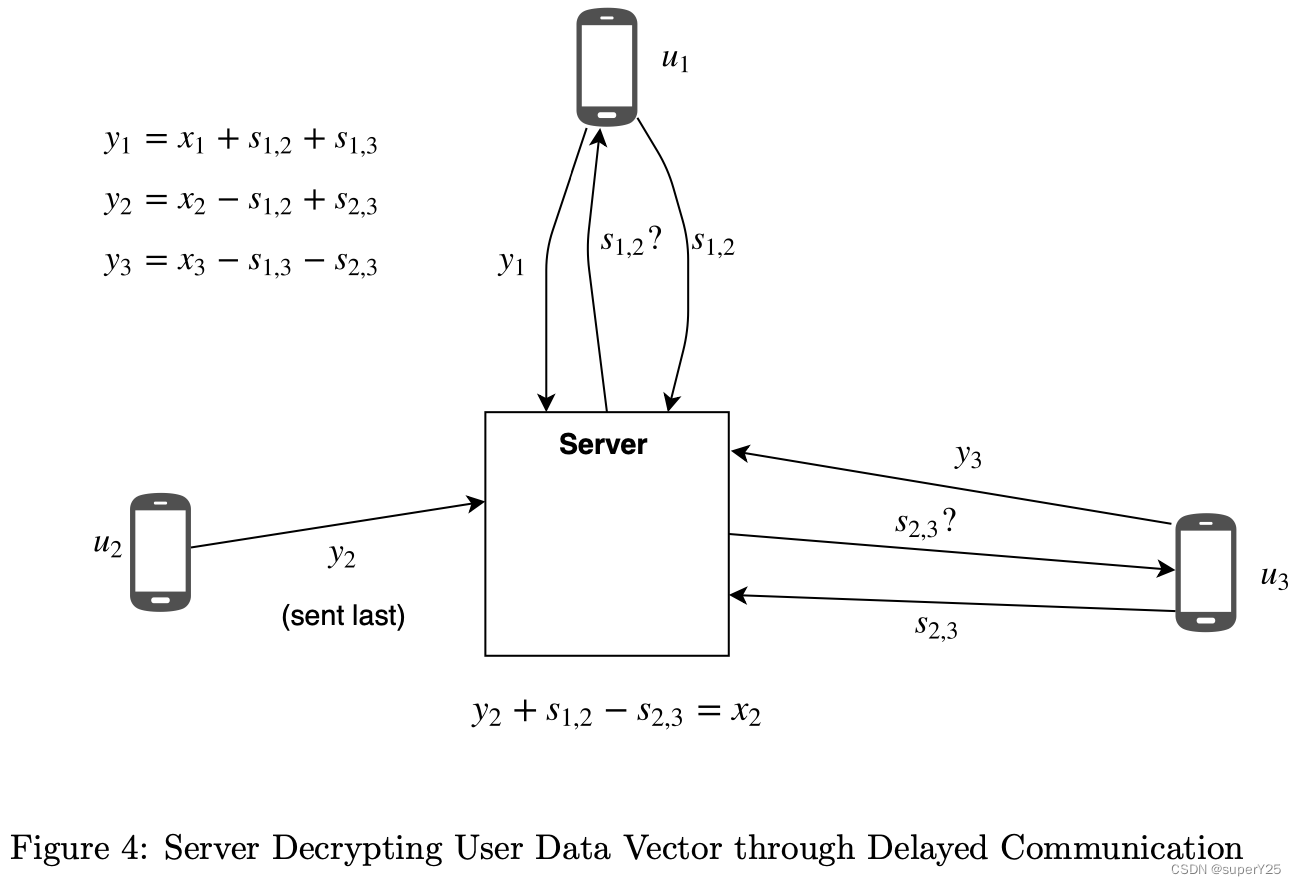
《Secure Analytics-Federated Learning and Secure Aggregation》论文阅读
背景 机器学习模型对数据的分析具有很大的优势,很多敏感数据分布在用户各自的终端。若大规模收集用户的敏感数据具有泄露的风险。 对于安全分析的一般背景就是认为有n方有敏感数据,并且不愿意分享他们的数据,但可以分享聚合计算后的结果。 联…...
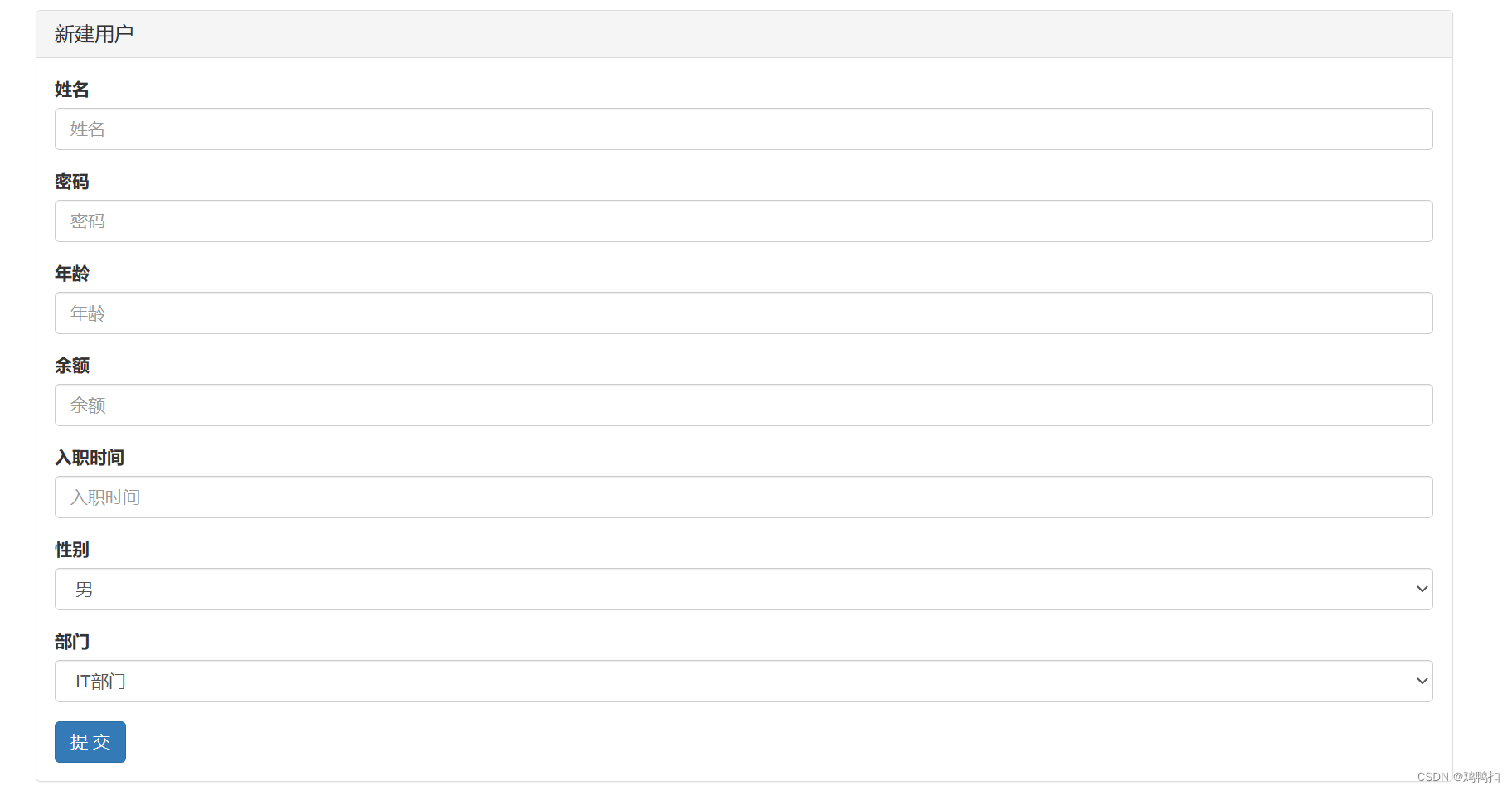
十三、Django之添加用户(原始方法实现)
修改urls.py path("user/add/", views.user_add),添加user_add.html {% extends layout.html %} {% block content %}<div class"container"><div class"panel panel-default"><div class"panel-heading"><h3 c…...

Elasticsearch数据操作原理
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...

gitgitHub
在git中复制CtrlInsert、粘贴CtrlShif 一、用户名和邮箱的配置 查看用户名 :git config user.name 查看密码: git config user.password 查看邮箱:git config user.email 查看配置信息: $ git config --list 修改用户名 git co…...
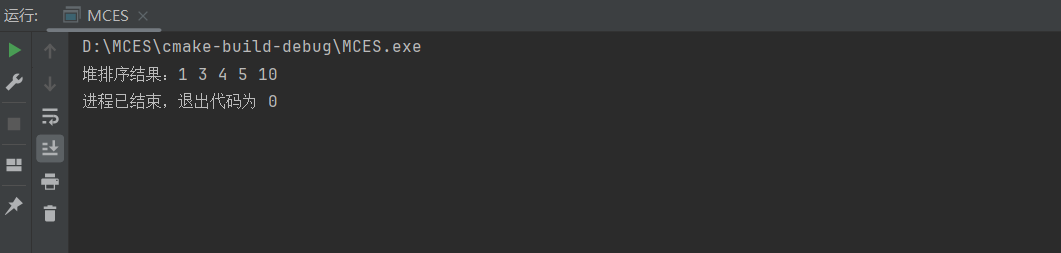
十天学完基础数据结构-第九天(堆(Heap))
堆的基本概念 堆是一种特殊的树形数据结构,通常用于实现优先级队列。堆具有以下两个主要特点: 父节点的值始终大于或等于其子节点的值(最大堆),或者父节点的值始终小于或等于其子节点的值(最小堆ÿ…...
vertx的学习总结7之用kotlin 与vertx搞一个简单的http
这里我就简单的聊几句,如何用vertx web来搞一个web项目的 1、首先先引入几个依赖,这里我就用maven了,这个是kotlinvertx web <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apac…...
:链路追踪)
golang学习笔记(二):链路追踪
自定义http连接的服务端 package serverimport ("github.com/gin-gonic/gin""go.opentelemetry.io/contrib/instrumentation/github.com/gin-gonic/gin/otelgin""net/http" )type MyServer struct {Server *http.Server }func GetServer() *MyS…...
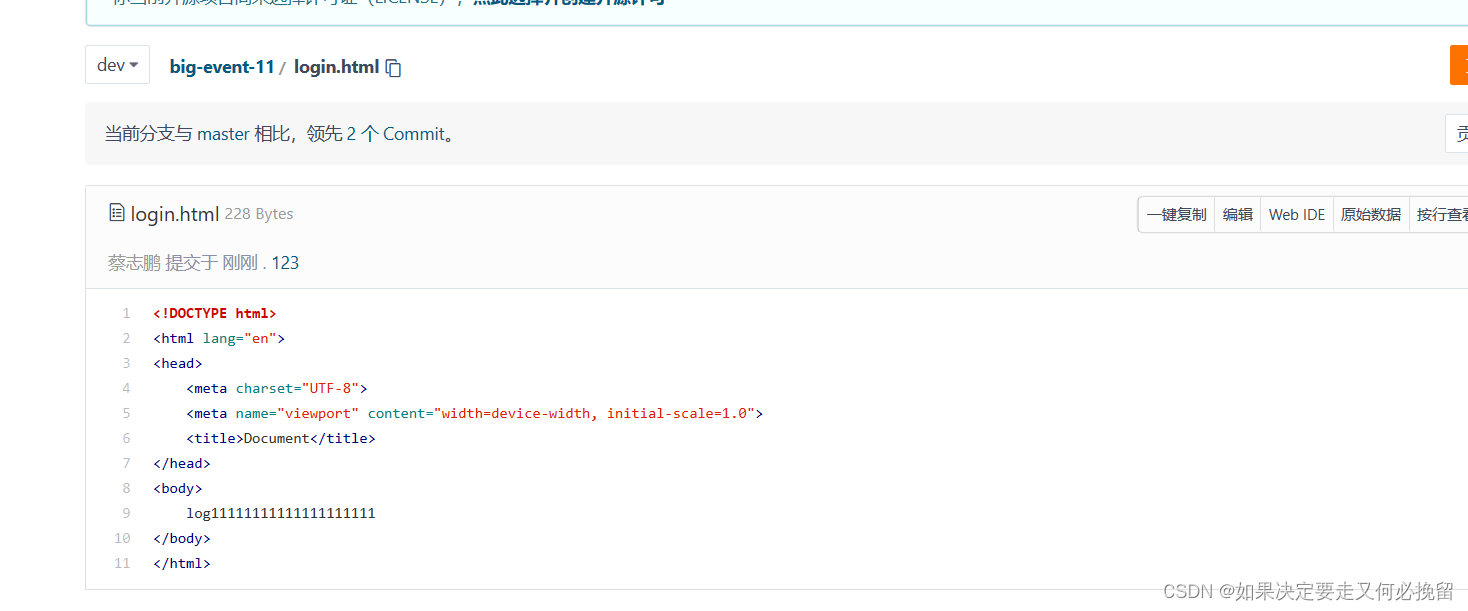
git提交代码实际操作
1.仓库的代码 2.克隆代码下存在的分支 git clobe https://gitee.com/sadsadasad/big-event-11.git 3.查看当下存在的分支 git branch -a 在很多情况下,我们是要围绕着dev分支进行开发,所以我们可以在开发之前问明白围绕那个分支进行开发。 4.直接拉去dev分支代码 5.如果没在…...
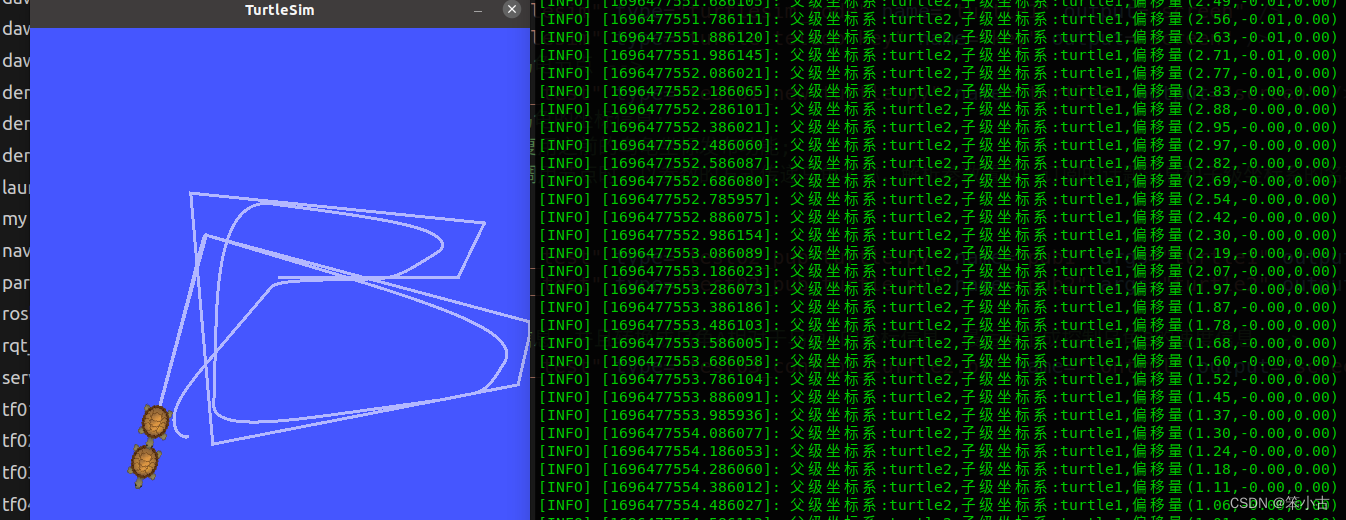
TF坐标变换
ROS小乌龟跟随 5.1 TF坐标变换 Autolabor-ROS机器人入门课程《ROS理论与实践》零基础教程 tf模块:在 ROS 中用于实现不同坐标系之间的点或向量的转换。 在ROS中坐标变换最初对应的是tf,不过在 hydro 版本开始, tf 被弃用,迁移到 tf2,后者更…...

如何进行网络编程和套接字操作?
网络编程是计算机编程中重要的领域之一,它使程序能够在网络上进行数据传输和通信。C语言是一种强大的编程语言,也可以用于网络编程。网络编程通常涉及套接字(Socket)操作,套接字是一种用于网络通信的抽象接口。本文将详…...

在Spark中集成和使用Hudi
本文介绍了在Spark中集成和使用Hudi的功能。使用Spark数据源API(scala和python)和Spark SQL,插入、更新、删除和查询Hudi表的代码片段。 1.安装 Hudi适用于Spark-2.4.3+和Spark 3.x版本。 1.1 Spark 3支持矩阵 Hudi...
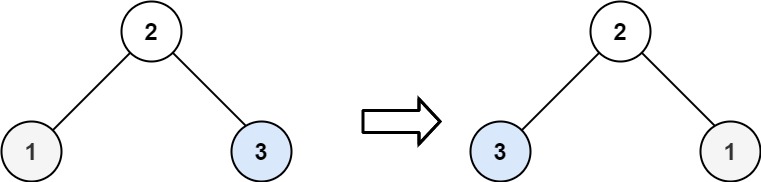
力扣第226翻转二叉数 c++三种方法 +注释
题目 226. 翻转二叉树 简单 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 1: 输入:root [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]示例 2: 输入:root [2,1,3] 输出&am…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
