UVa11324 - The Largest Clique
Online Judge
题目大意:有一张n个点m条边的图,现对于每一个点u,建立一条边连接它和所有它能到达的点,问满足所有点之间都有边的分量的大小最大是多少
0<=n<=1000;0<=m<=50000
思路:根据建新图的规则可知,一个点会和它能到达的所有点构成一个合法的分量,那么从入度为0的点开始组成的这样一个分量一定是最大的,但是因为图中有环,所以没法直接统计这样的分量的大小,所以要先用tarjan将所有强量通分量缩成一个点,再在新图中用记忆化搜索找上述的分量
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int head[N], head2[N];
struct Edge
{int v, next;
}e[N * N], e2[N * N];
int dfn[N], low[N];
int c1 = 0, c2 = 0;
void addedge(int u, int v)
{//原图e[++c1].v = v;e[c1].next = head[u];head[u] = c1;
}
void addedge2(int u, int v)
{//缩点后的新图e2[++c2].v = v;e2[c2].next = head2[u];head2[u] = c2;
}
bool vis[N];
int cnt = 0;
int ans = 0;
stack<int>s;
int siz[N];
pair<int, int>edge[N * N];
int n, m;
int cnts[N];
int scc[N];
void tarjan(int u)
{//将图拆解成强连通分量的组合cnt++;//访问次序dfn[u] = low[u] = cnt;//每个点的访问次序,在第几个强连通分量里 s.push(u);//储存dfs中待处理的点vis[u] = 1;//在栈内待处理for (int i = head[u]; ~i; i=e[i].next){int v = e[i].v;if (!dfn[v]){//子节点没被访问过tarjan(v);low[u] = min(low[u], low[v]);//和子节点合并成一个强连通分量}else if (vis[v]){//重复访问了栈内的节点low[u] = min(low[u], low[v]);//这两个点一定在一个强连通分量内}}if (dfn[u] == low[u]){//当前点是这个强连通分量的第一个点,也就是这个分量都已处理完毕int temp = 0;//记录强连通分量的点数ans++;//第几个强连通分量while (!s.empty() && s.top() != u){//将这个强量通分量内的点全部弹出 vis[s.top()] = 0;//不在栈内scc[s.top()] = ans;//每个点属于哪个强连通分量temp++;s.pop();}temp++;vis[s.top()] = 0;//第一个点也要弹出scc[s.top()] = ans;s.pop();siz[ans] = temp;//这个连通块里面几个点}
}
int in[N];
void init()
{c1 = c2 = 0;for (int i = 1; i <= n; i++){vis[i] = 0;dfn[i] = low[i] = siz[i] = 0;head[i] = head2[i] = -1;cnts[i] = 0;in[i] = 0;}while (!s.empty()){s.pop();}cnt = ans = 0;
}
int dfs(int u)
{//记忆化搜索能到达多少个点if (cnts[u]){return cnts[u];}int ma = 0;for (int i = head2[u]; ~i; i=e2[i].next){int v = e2[i].v;ma = max(ma, dfs(v));//取子节点里面最大的}cnts[u] = siz[u] + ma;//这个歌两桶快的大小加子节点传来的值return cnts[u];
}
void solve()
{cin >> n >> m;init();for (int i = 1; i <= m; i++){int u, v;cin >> u >> v;edge[i] = { u,v };addedge(u, v);}for (int i = 1; i <= n; i++){if (!dfn[i])//所有没处理的点都要处理tarjan(i);}for (int i = 1; i <= m; i++){int u = edge[i].first, v = edge[i].second;if (scc[u] != scc[v]){//两个点不在一个强连通分块里addedge2(scc[u], scc[v]);//建新图in[scc[v]]++;}}int out = 0;for (int i = 1; i <= n; i++){if (!in[i]){//从入度为0的点出发开始搜out = max(out, dfs(i));}}cout << out << '\n';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);int t;cin >> t;while (t--){solve();}return 0;
}相关文章:

UVa11324 - The Largest Clique
Online Judge 题目大意:有一张n个点m条边的图,现对于每一个点u,建立一条边连接它和所有它能到达的点,问满足所有点之间都有边的分量的大小最大是多少 0<n<1000;0<m<50000 思路:根据建新图的规则可知&am…...

【Linux】TCP的服务端(守护进程) + 客户端
文章目录 📖 前言1. 服务端基本结构1.1 类成员变量:1.2 头文件1.3 初始化:1.3 - 1 全双工与半双工1.3 - 2 inet_aton1.3 - 3 listen 2. 服务端运行接口2.1 accept:2.2 服务接口: 3. 客户端3.1 connect:3.2 …...

1.7. 找出数组的第 K 大和原理及C++实现
题目 给你一个整数数组 nums 和一个 正 整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。 数组的 第 k 大和 定义为:可以获得的第 k 个 最大 子序列和(子序列和允许出现重复) 返回数组的 第 k 大和 。 子序列是一个可以由其他数…...
基于微信小程序的付费自习室
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 文章目录 1 简介2 技术栈3 需求分析3.1用户需求分析3.1.1 学生用户3.1.3 管理员用户 4 数据库设计4.4.1 E…...

纪念在CSDN的2048天
时间真快~...

云原生Kubernetes:简化K8S应用部署工具Helm
目录 一、理论 1.HELM 2.部署HELM2 3.部署HELM3 二、实验 1.部署 HELM2 2.部署HELM3 三、问题 1.api版本过期 2.helm初始化报错 3.pod状态为ImagePullBackOff 4.helm 命令显示 no repositories to show 的错误 5.Helm安装报错 6.git命令报错 7.CentOS 7 下git c…...

qml保姆级教程五:视图组件
💂 个人主页:pp不会算法v 🤟 版权: 本文由【pp不会算法v】原创、在CSDN首发、需要转载请联系博主 💬 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦 QML系列教程 QML教程一:布局组件 文章目录 列表视图ListVi…...

2310d编译不过
struct A {this(int[] data) safe { a data; }int[] a; }void main() safe {int[3] test [1, 2, 3];A a A(test); }应该给data参数加上return scope.或让构造器为模板参数来推导,否则,构造器可以把栈分配切片赋值给全局变量....
CleanMyMac X4.14.1最新版本下载
CleanMyMac X是一个功能强大的Mac清理软件,它的设计理念是提供多个模块,包括垃圾清理、安全保护、速度优化、应用程序管理和文档管理粉碎等,以满足用户的不同需求。软件的界面简洁直观,让用户能够轻松进行日常的清理操作。 使用C…...
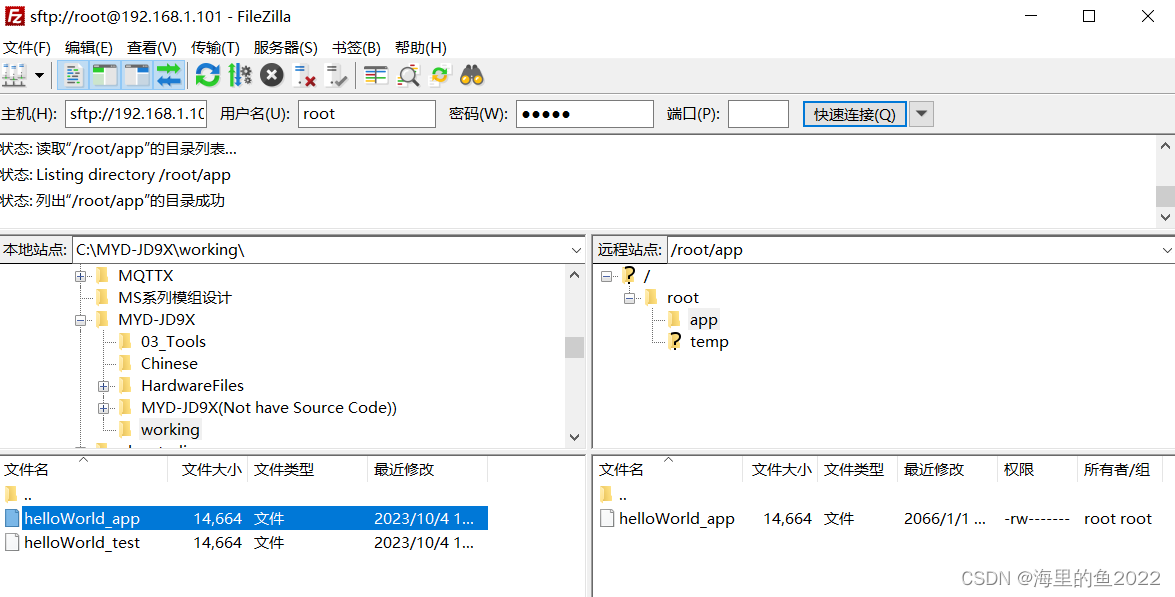
芯驰D9评测(3)--建立开发环境
1. 建立交叉编译链接环境 官网下载的SDK包中就有交叉工具链,米尔提供的这个 SDK 中除了包含各种源代码外还提供了必要的交叉工具链,可以直接用于编译应用程序等。 用户可以直接使用次交叉编译工具链来建立一个独立的开发环境,可单独编译…...
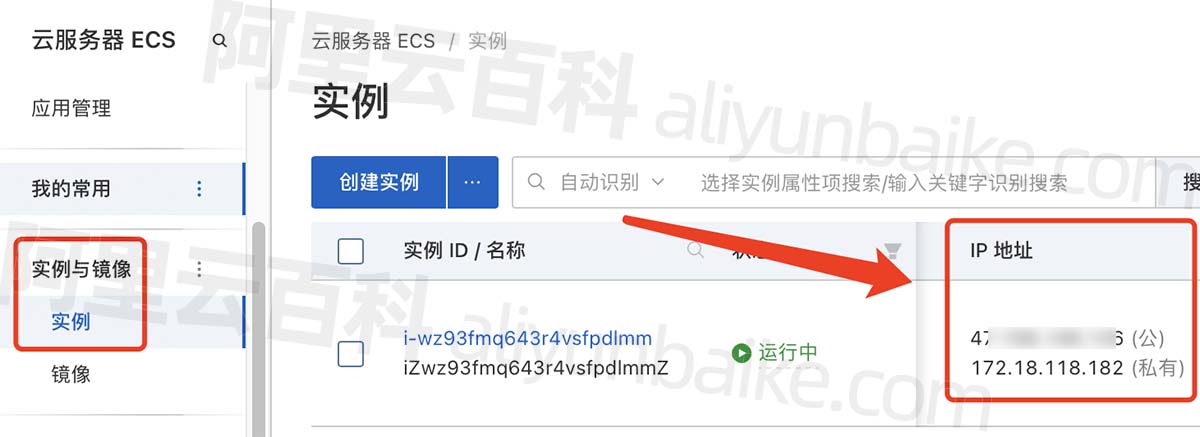
阿里云服务器IP地址查询方法(公网IP和私网IP)
阿里云服务器IP地址在哪查看?在云服务器ECS管理控制台即可查看,阿里云服务器IP地址包括公网IP和私有IP地址,阿里云百科分享阿里云服务器IP地址查询方法: 目录 阿里云服务器IP地址查询 阿里云服务器IP地址查询 1、登录到阿里云服…...

第47节——使用bindActionCreators封装actions模块
一、什么是action creators 1、概念 在Redux中,Action Creators是一种函数,它用于创建一个描述应用程序状态变化的action对象。Action对象是一个普通JavaScript对象,它包含一个描述action类型的字符串属性(通常称为“type”&…...

QT、c/c++通过宏自动判断平台
QT、c/c通过宏自动判断平台 Chapter1 QT、c/c通过宏自动判断平台 Chapter1 QT、c/c通过宏自动判断平台 原文链接:https://blog.csdn.net/qq_32348883/article/details/123063830 背景 为了更好的进行跨平台移植、编译、调试。 具体操作 宏操作 #ifdef _WIN32//d…...

对比表:阿里云轻量应用服务器和服务器性能差异
阿里云服务器ECS和轻量应用服务器有什么区别?轻量和ECS优缺点对比,云服务器ECS是明星级云产品,适合企业专业级的使用场景,轻量应用服务器是在ECS的基础上推出的轻量级云服务器,适合个人开发者单机应用访问量不高的网站…...
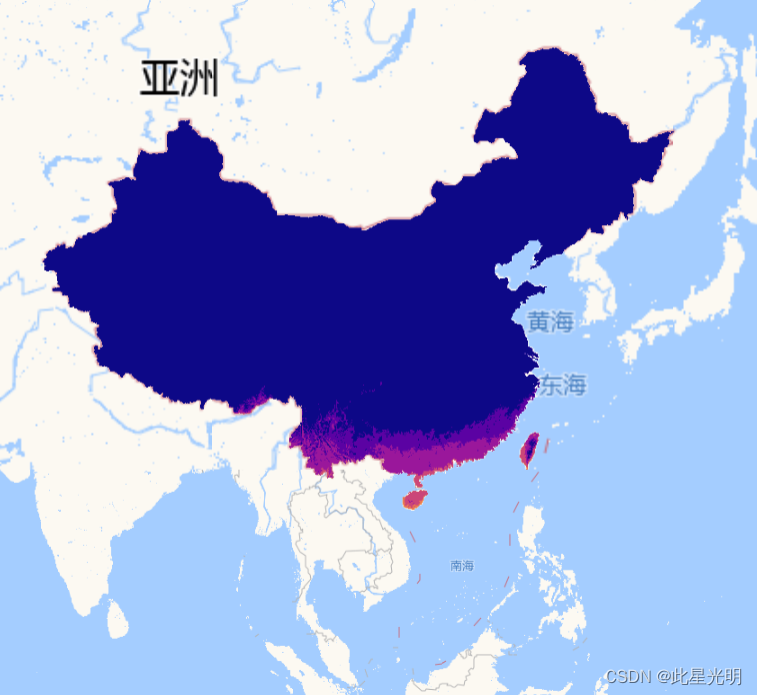
中国1km分辨率月最低温和最高温度数据集(1901-2020)
简介: 中国1km分辨率月最低温度数据集(1901-2020)是根据CRU发布的全球0.5气候数据集以及WorldClim发布的全球高分辨率气候数据集,通过Delta空间降尺度方案在中国地区降尺度生成的。使用了496个独立气象观测点数据进行验证&#x…...
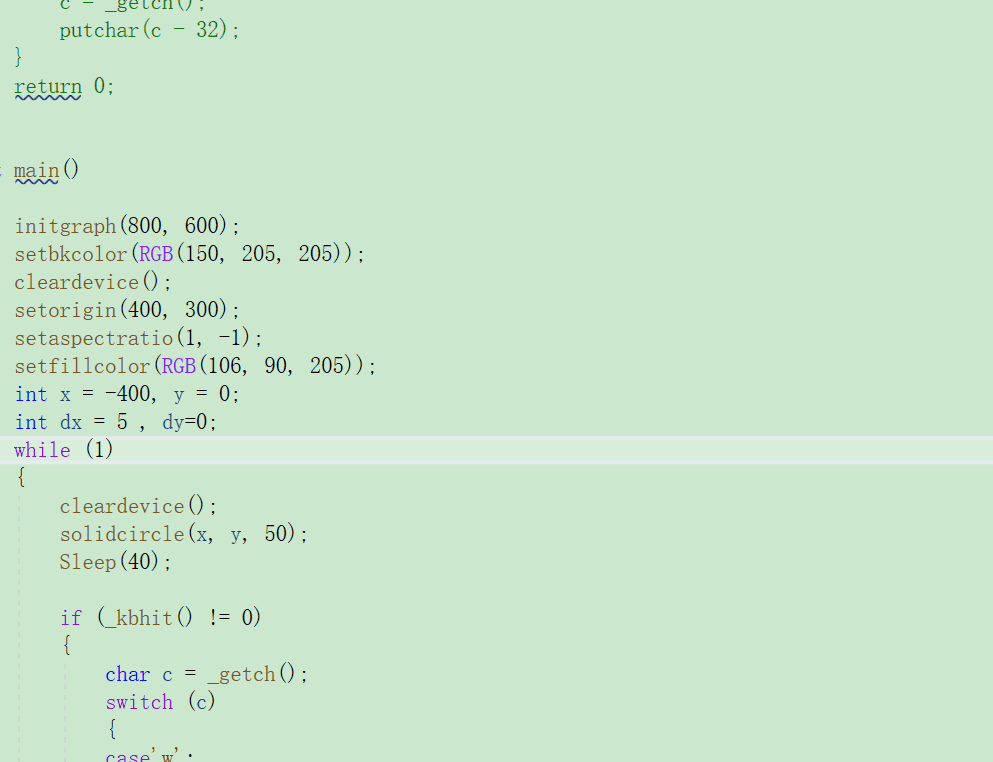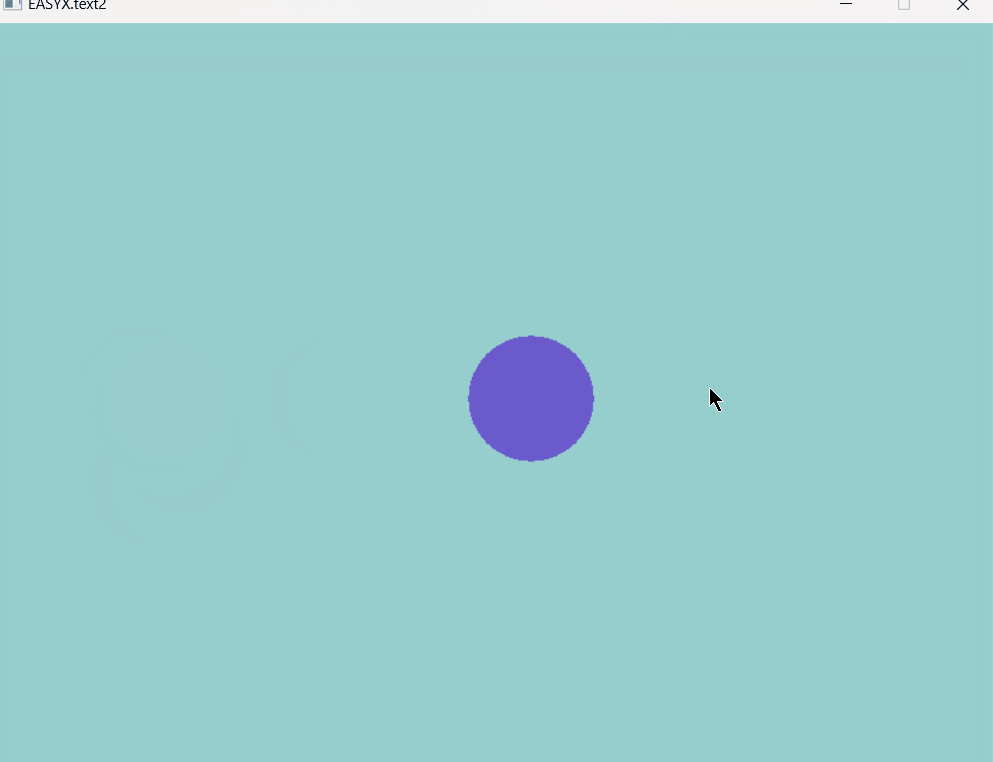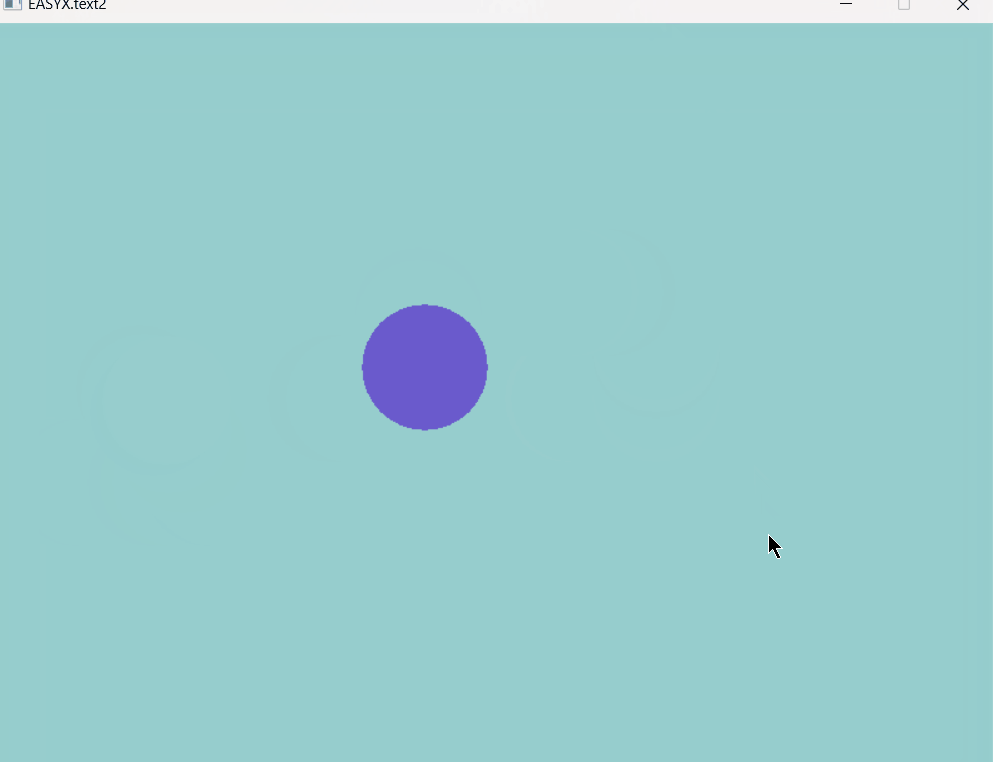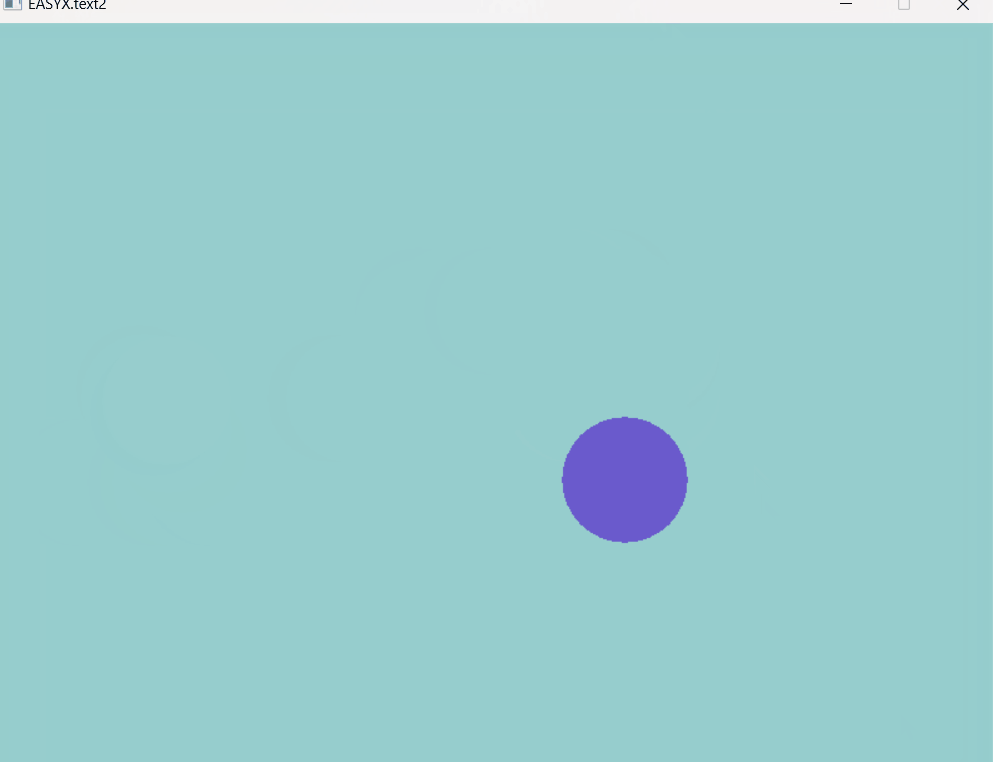
EasyX图形库note4,动画及键盘交互
大家好,这里是Dark Flame Master,专栏从这篇开始就会变得很有意思,我们可以利用今天所学的只是实现很多功能,同样为之后的更加好玩的内容打下基础,从这届开始将会利用所学的知识制作一些小游戏,废话不多说&…...
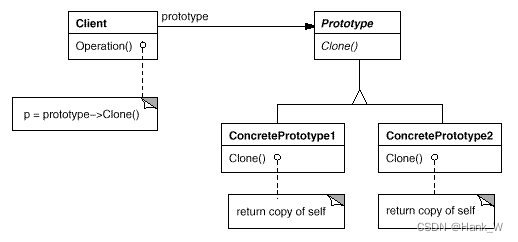
C++设计模式-原型(Prototype)
目录 C设计模式-原型(Prototype) 一、意图 二、适用性 三、结构 四、参与者 五、代码 C设计模式-原型(Prototype) 一、意图 用原型实例指定创建对象的种类,并且通过拷贝这些原型创建新的对象。 二、适用性 当…...

[补题记录] Atcoder Beginner Contest 322(E)
URL:https://atcoder.jp/contests/abc322 目录 E Probelm/题意 Thought/思路 Code/代码 E Probelm/题意 有 N 个改进计划,每个计划可以执行一次;有 K 个参数,每个计划可以将所有参数提升固定值,即计划 i 可以为第…...

目标检测算法改进系列之Backbone替换为FocalNet
FocalNet 近些年,Transformers在自然语言处理、图像分类、目标检测和图像分割上均取得了较大的成功,归根结底是自注意力(SA :self-attention)起到了关键性的作用,因此能够支持输入信息的全局交互。但是由于…...
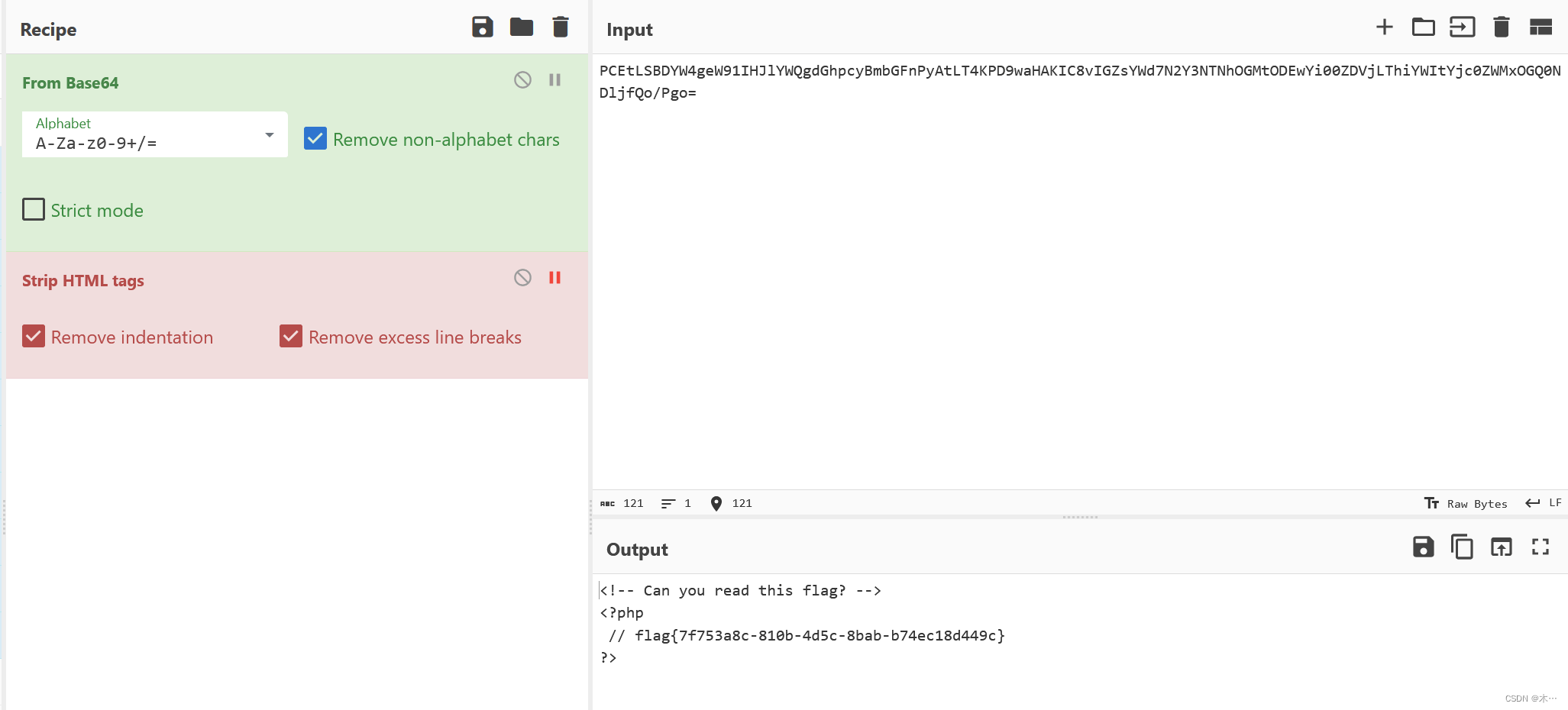
buuctf-[BSidesCF 2020]Had a bad day 文件包含
打开环境 就两个按钮,随便按按 url变了 还有 像文件包含,使用php伪协议读取一下,但是发现报错,而且有两个.php,可能是自己会加上php后缀 所以把后缀去掉 /index.php?categoryphp://filter/convert.base64-encode/resourcei…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
