karmada v1.7.0安装指导
前言
安装心得
经过多种方式操作,发现二进制方法安装太复杂,证书生成及其手工操作太多了,没有安装成功;helm方式的安装,v1.7.0的chart包执行安装会报错,手工修复了报错并修改了镜像地址,还是各种啦不下来镜像,安装失败。最后使用了kubectl karmada init的方式安装成功了。
此外,官方文档要求条件如下:
前提条件
- Go v1.18+
- kubectl v1.19+
详细安装步骤
1、从github上下载karmada的v1.7.0的版本
Release Karmada v1.7.0 release · karmada-io/karmada · GitHub
安装过程中用到的文件如下,这些包是需要下载的
Source code(zip)
crds.tar.gz
2、安装Go SDK
- 下载软件包All releases - The Go Programming Language,我们这里使用的是
go1.20.4.linux-amd64.tar.gz
把软件包go1.20.4.linux-amd64.tar.gz上传到/root下面,执行如下命令解压
tar -C /usr/local -xzf go1.20.4.linux-amd64.tar.gz
- 添加环境变量
vi /etc/profile
- 把如下内容添加进去
export PATH=$PATH:/usr/local/go/bin
export GOPROXY=https://goproxy.io,direct
- 执行如下命令生效
source /etc/profile
- 执行如下命令,显示如下内容,表示安装成功
# go version
go version
显示信息如下,
go version go1.20.4 linux/amd64
3、从源代码编译karmada二进制文件。
cd karmada
make karmada-aggregated-apiserver karmada-controller-manager karmada-scheduler karmada-webhook karmadactl kubectl-karmada
cd _output/bin/linux/amd64/
mv karmadactl kubectl-karmada /usr/local/sbin/
4、通过 Karmada 命令行工具安装 Karmada
参考链接:安装概述 | karmada
执行如下命令:
kubectl karmada init --crds /root/karmada-install2023/crds.tar.gz --kube-image-registry=registry.aliyuncs.com/google_containers --kube-image-tag='v1.25.4' --karmada-aggregated-apiserver-image='docker.io/karmada/karmada-aggregated-apiserver' --karmada-controller-manager-image='docker.io/karmada/karmada-controller-manager' --karmada-scheduler-image='docker.io/karmada/karmada-scheduler' --karmada-webhook-image='docker.io/karmada/karmada-webhook'
执行结果如下,表示安装成功:
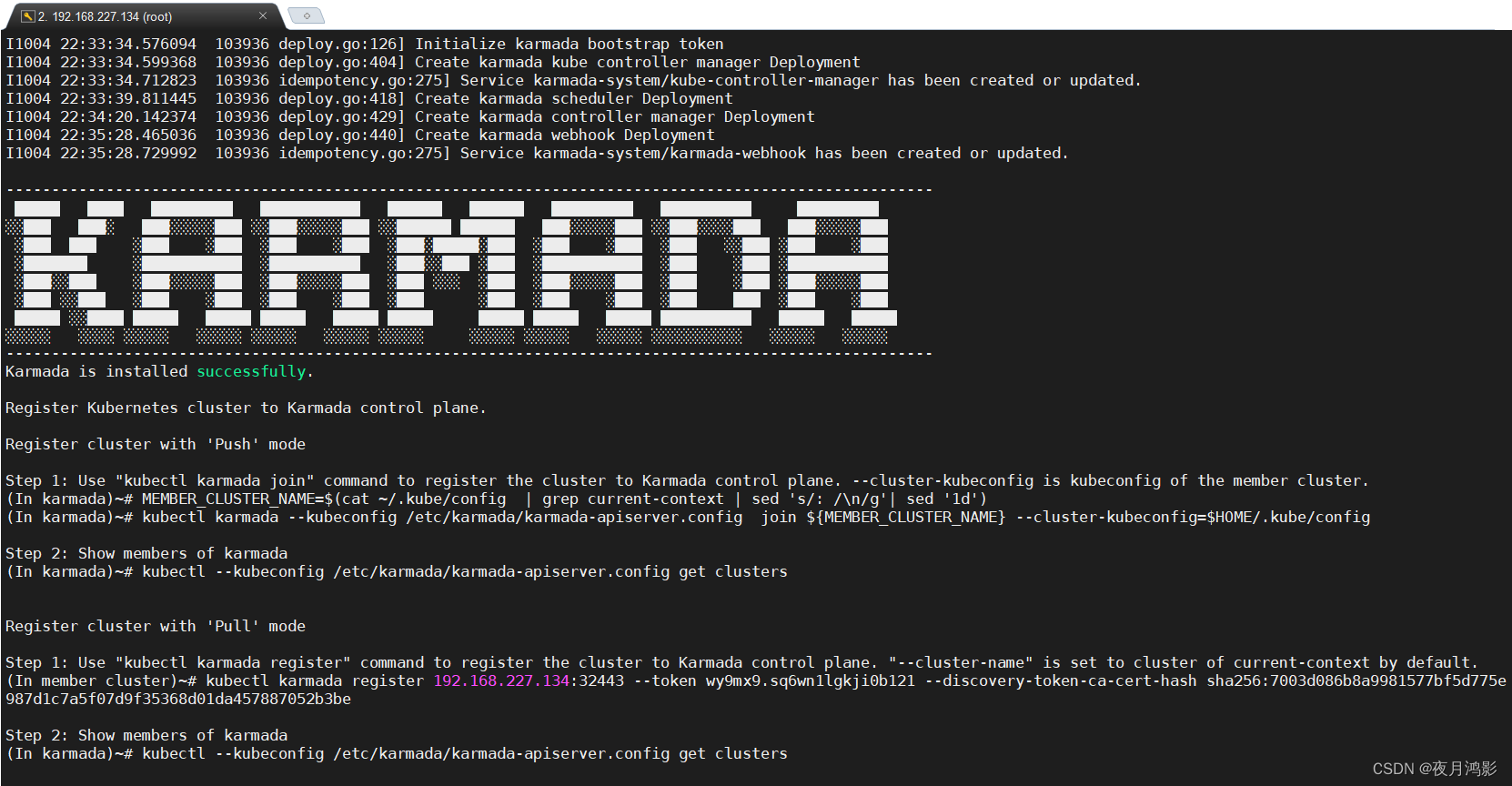
可以查看更多帮助命令:
kubectl karmada init --help
5、安装完成,结果查看
kubectl -n karmada-system get pod
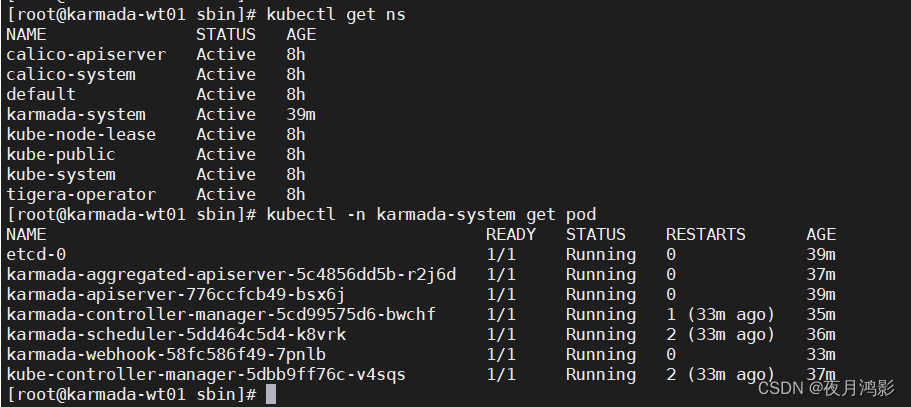
相关文章:

karmada v1.7.0安装指导
前言 安装心得 经过多种方式操作,发现二进制方法安装太复杂,证书生成及其手工操作太多了,没有安装成功;helm方式的安装,v1.7.0的chart包执行安装会报错,手工修复了报错并修改了镜像地址,还是各…...
OK3568 forlinx系统编译过程及问题汇总
1. 共享文件夹无法加载;通过网上把文件夹加载后,拷贝文件很慢,任务管理器查看发现硬盘读写速率很低。解决办法:重新安装vmware tools。 2. 拷贝Linux源码到虚拟机,解压。 3. 虚拟机基本库安装 forlinxubuntu:~$ sudo…...

JVM篇---第五篇
系列文章目录 文章目录 系列文章目录一、简述Java的对象结构二、如何判断对象可以被回收?三、JVM的永久代中会发生垃圾回收么?一、简述Java的对象结构 Java对象由三个部分组成:对象头、实例数据、对齐填充。 对象头由两部分组成,第一部分存储对象自身的运行时数据:哈希码…...

C/C++ 排序算法总结
1.冒泡排序 https://blog.csdn.net/weixin_49303682/article/details/119365319 1 #include <stdio.h>2 3 #define N 94 5 void print(int a[])6 {7 for(int i 0; i < N; i)8 {9 printf("%d ", a[i]); 10 } 11 printf("…...
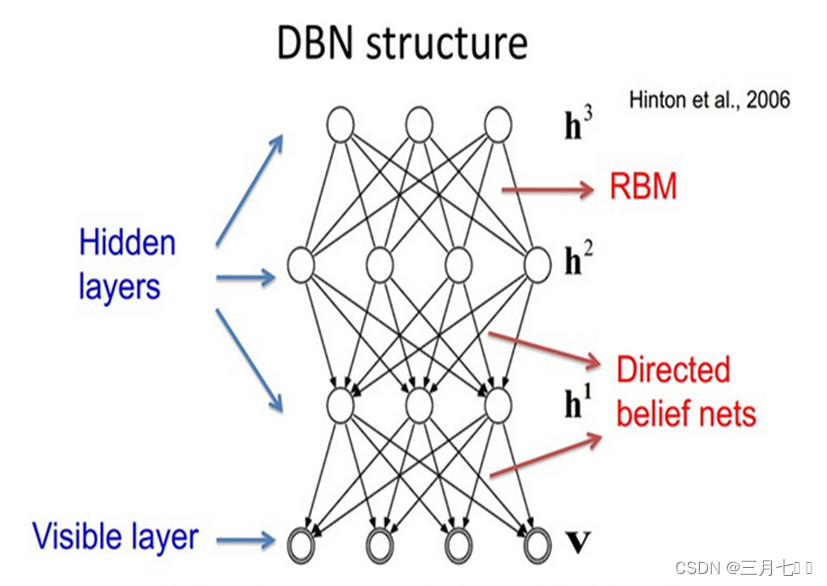
机器学习---RBM、KL散度、DBN
1. RBM 1.1 BM BM是由Hinton和Sejnowski提出的一种随机递归神经网络,可以看做是一种随机生成的 Hopfield网络,是能够通过学习数据的固有内在表示解决困难学习问题的最早的人工神经网络之 一,因样本分布遵循玻尔兹曼分布而命名为BM。BM由二…...
有序序列合并)
(c语言)有序序列合并
#include<stdio.h>//输入包含三行 //第一行包含两个正整数n,m,用空格分割,n表示第二行第一个升序序列中 //数字的个数,m表示第三行第二个升序序列中数字的个数 //第二行包含n个整数,用空格分割 //第三行包含m个整数,用空格分割 //输出…...
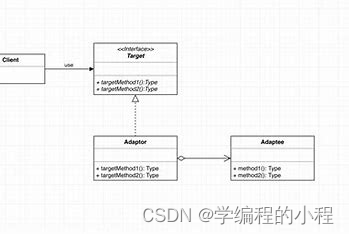
小谈设计模式(18)—适配器模式
小谈设计模式(18)—适配器模式 专栏介绍专栏地址专栏介绍 适配器模式角色分析目标接口(Target)源接口(Adaptee)适配器(Adapter) 核心思想应用场景Java程序实现输出结果程序分析123 优…...
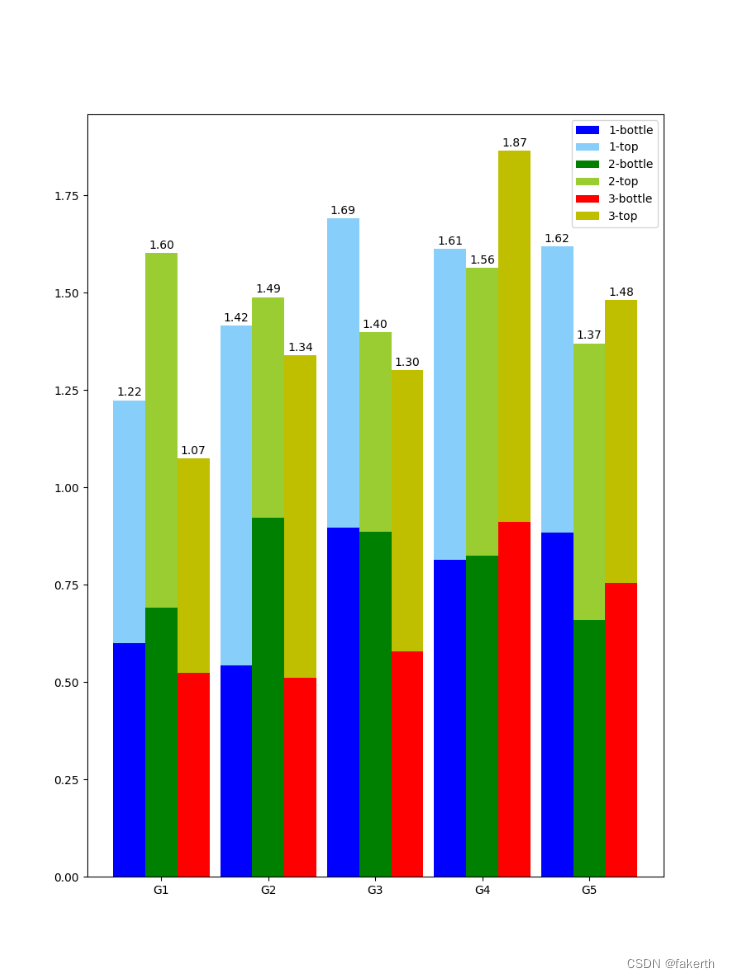
Python柱形图
柱形图 柱形图,又称长条图、柱状统计图、条图、条状图、棒形图,是一种以长方形的长度为变量的统计图表。长条图用来比较两个或以上的价值(不同时间或者不同条件),只有一个变量,通常利用于较小的数据集分析…...
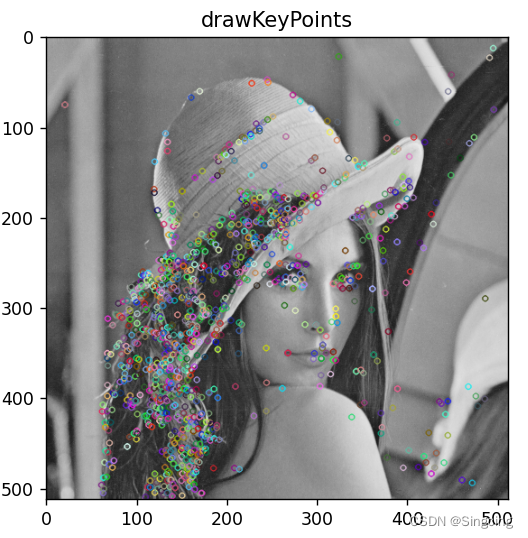
用OpenCV(Python)获取图像的SIFT特征
import cv2 as cv import numpy as np import matplotlib.pyplot as plt imgcv.imread("../Lena.png") img_graycv.cvtColor(img,cv.COLOR_BGR2GRAY)#创建一个SIFI对象 siftcv.SIFT_create()#使用SIFT对象在灰度图像img_gray中检测关键点,结果存储在变量k…...

阿里云ECS和轻量服务器有什么区别?
阿里云服务器ECS和轻量应用服务器有什么区别?轻量和ECS优缺点对比,云服务器ECS是明星级云产品,适合企业专业级的使用场景,轻量应用服务器是在ECS的基础上推出的轻量级云服务器,适合个人开发者单机应用访问量不高的网站…...
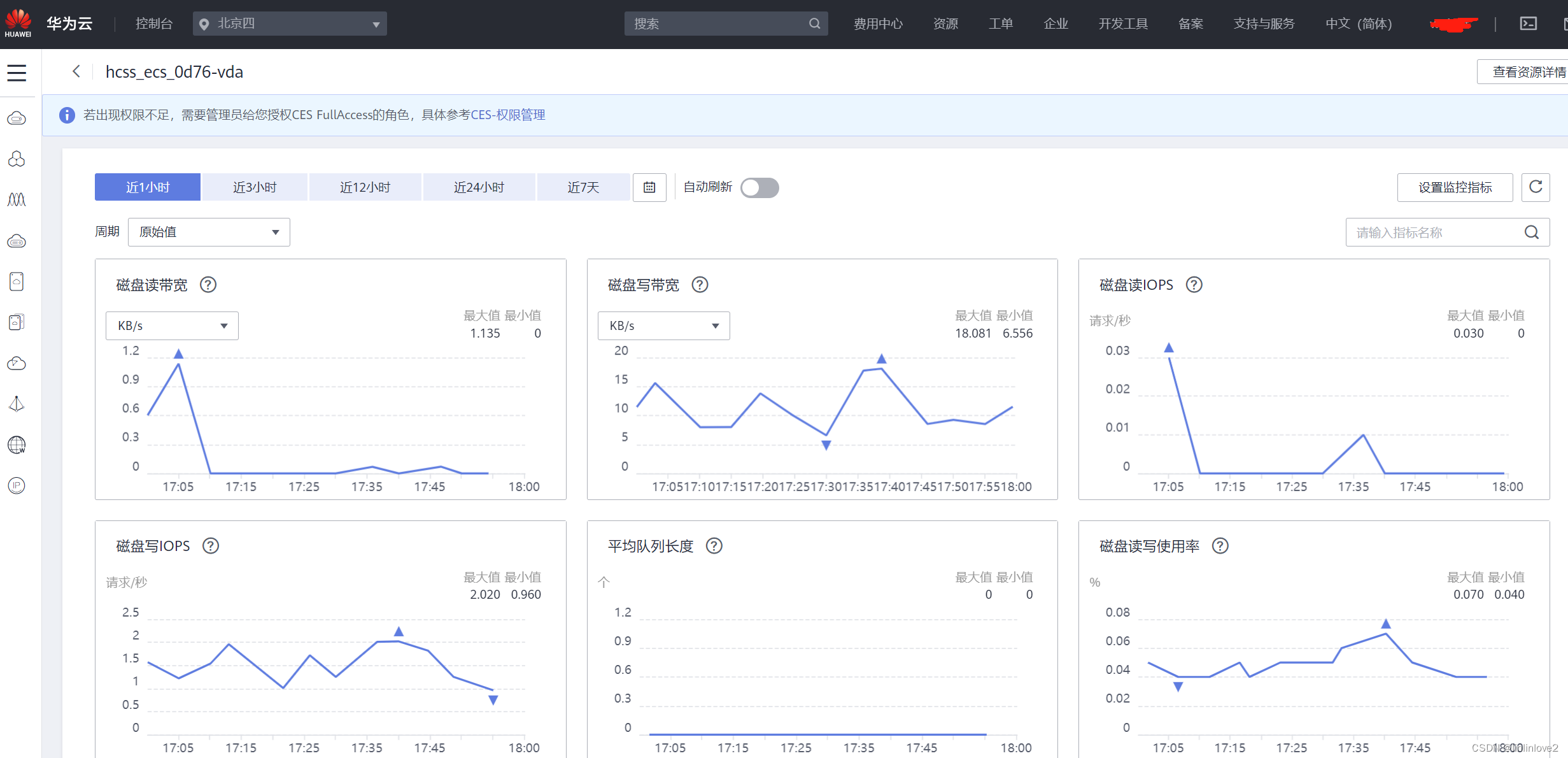
华为云云耀云服务器L实例评测|安装搭建学生成绩管理系统
1.前言概述 华为云耀云服务器L实例是新一代开箱即用、面向中小企业和开发者打造的全新轻量应用云服务器。多种产品规格,满足您对成本、性能及技术创新的诉求。云耀云服务器L实例提供丰富严选的应用镜像,实现应用一键部署,助力客户便捷高效的在…...
Audacity 使用教程:轻松录制、编辑音频
Audacity 使用教程:轻松录制、编辑音频 1. 简介 Audacity 是一款免费、开源且功能强大的音频录制和编辑软件。它适用于 Windows、Mac 和 Linux 等多种操作系统,适合音乐制作、广播后期制作以及普通用户进行音频处理。本教程将带领大家熟悉 Audacity 的…...

深入了解“注意力”和“变形金刚”-第2部分
一、说明 在上一个故事中,我已经解释了什么是注意力机制,以及与转换器相关的一些重要关键字和块,例如自我注意、查询、键和值以及多头注意力。 在这一部分中,我将解释这些注意力块如何帮助创建转换器网络,并详细讨论网…...

“债务飙升!美国一天内增加2750亿美元,金融震荡的前奏已拉开帷幕!”
2023年10月4日,美国政府向美国债务追加2750亿美元,相当于现在比特币(BTC)总市值的一半还多。 有人会说:多一点、少一点,没什么区别.....确实,当你看美国债务时,2750亿美元并没有什么意义&#x…...

最新Uniapp软件社区-全新带勋章源码
测试环境:php7.1。ng1.2,MySQL 5.6 常见问题: 配置好登录后转圈圈,检查环境及伪静态以及后台创建好应用 上传图片不了,检查php拓展fileinfo 以及public文件权限 App个人主页随机背景图,在前端uitl文件夹里面…...

基于goravel的CMS,企业官网通用golang后台管理系统
2023年9月11日10:47:00 仓库地址: https://gitee.com/open-php/zx-goravel-website 框架介绍 Goravel SCUI 后端开发组件 go 1.20 Goravel 1.13 数据库 sql(使用最新日期文件) goravel\doc\sql_bak mysql 8.0 前端开发组件 scui 1.6.9 node v14.21.3 效果图…...

(五)激光线扫描-位移台标定
线激光属于主动测量方式,但是由于线激光的特性,我们只能通过提取激光中心线获取这一条线上的高度信息,那么要进行三维重建的话,就需要通过平移或者是旋转的方式,来让线激光扫描被测物体的完整轮廓,也就是整个表面。激光线的密度越高还原出来的物体越细腻,但由于数据量大…...

媒体发稿:为什么选择国内媒体推广一文带你领略其魅
随着互联网的飞速发展,媒体推广成为企业宣传的重要方式。国内媒体推广因其独特的魅力和广泛的传播渠道,逐渐成为企业选择的首选。本文将探讨为什么选择国内媒体推广,并带您领略其魅力。 1. 国内媒体推广的广泛传播渠道 国内媒体推广拥有广泛…...

基于自私羊群优化的BP神经网络(分类应用) - 附代码
基于自私羊群优化的BP神经网络(分类应用) - 附代码 文章目录 基于自私羊群优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.自私羊群优化BP神经网络3.1 BP神经网络参数设置3.2 自私羊群算法应用 4.测试结果…...

AI绘图:GPT4技术的艺术化呈现与无限可能
了解更多点击《AI绘图:GPT4技术的艺术化呈现与无限可能》 GPT对于每个科研人员已经成为不可或缺的辅助工具,不同的研究领域和项目具有不同的需求。例如在科研编程、绘图领域: 1、编程建议和示例代码: 无论你使用的编程语言是Python、R、MATL…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
