数字IC前端学习笔记:数字乘法器的优化设计(华莱士树乘法器)
相关阅读
数字IC前端![]() https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
进位保留乘法器依旧保留着阵列的排列规则,只是进位是沿斜下角,如果能使用树形结构来规划这些进位保留加法器,就能获得更短的关键路径延迟和更小的器件开销,这种结构的乘法器被称为华莱士树乘法器。图1所示为使用四位华莱士树乘法器的例子,图中总共有十六个部分积,分别通过被乘数和乘数的各位相与(通过与门)得到,图中的斜杠/代表一个全加器,连接的分别是右上角的本位和以及左下角给高位的进位,带反斜杠\的/表示是半加器。
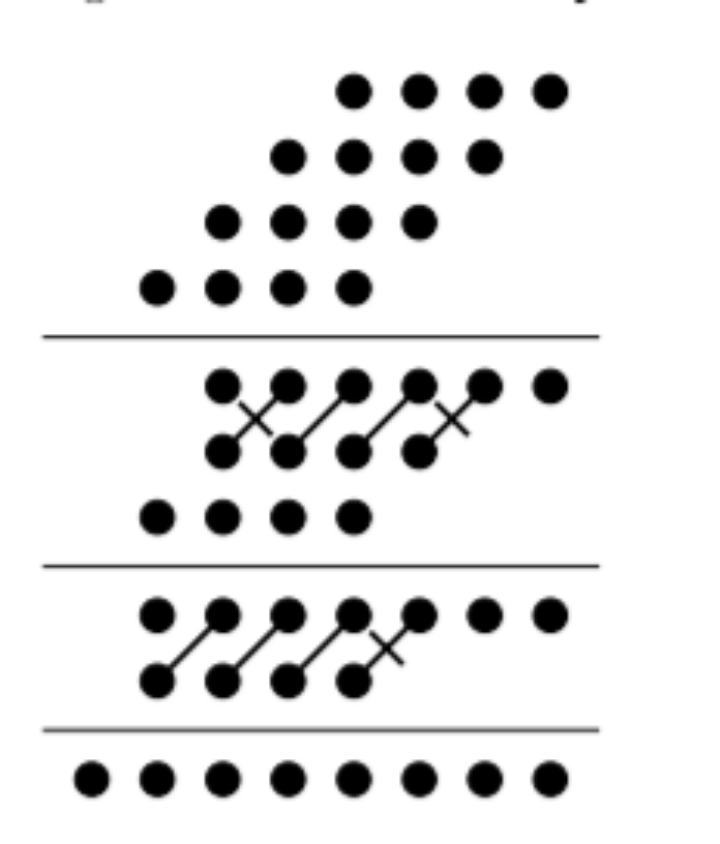
图1 华莱士树乘法器的覆盖过程
第一阶段华莱士将所有的部分积按行,每三行分组,在组内使用保留进位加法器(有全加器和半加器两种)压缩,当组内某一列含有三个部分积,则使用全加器压缩;若含有两个部分积,则使用半加器压缩,含有一个部分积,则不压缩。分组时的多余行不进行压缩,直接传递到下一阶段(在这里指的是第四行)。
下一阶段中,继续三行分一组,进行压缩,直到最后得到两行部分积,此时使用一个普通的多位传播进位加法器或者超前进位加法器等进行(两数相加)向量合并。可以看到只需要两个阶段,十六个部分积就可被压缩至两行。这个结构使用了五个全加器和三个半加器(不包括最后的向量合并器)。
具体的Verilog代码实现见附录,Modelsim软件仿真如图2所示。使用Synopsis的综合工具Design Compiler综合的结果如图3所示,综合使用了0.13μm工艺库。
 图2 华莱士树乘法器仿真结果
图2 华莱士树乘法器仿真结果
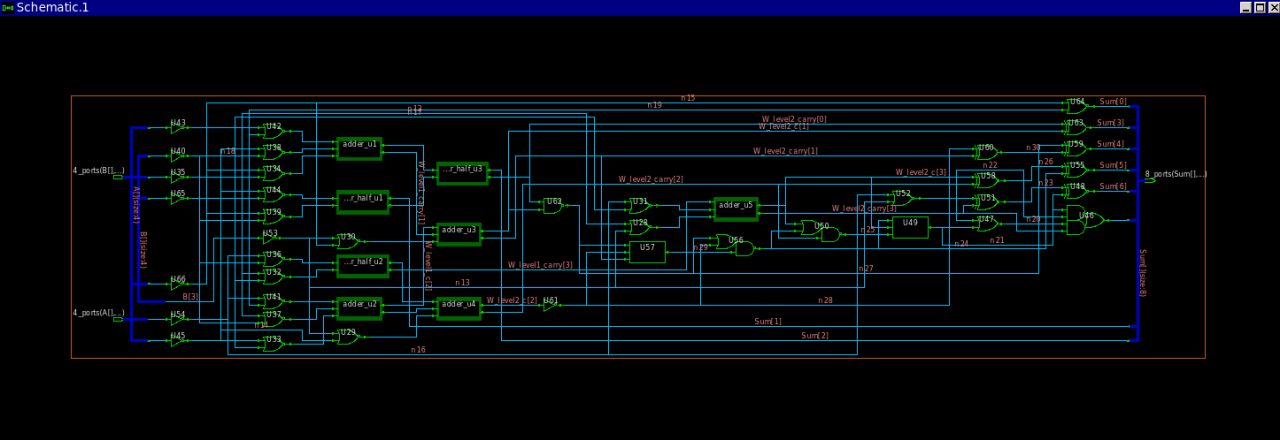 图3 华莱士树乘法器综合结果
图3 华莱士树乘法器综合结果
在Design Compiler中使用report_timing命令,可以得到关键路径的延迟,如图4所示,可以看出延迟仅有1.39ns。性能优于进位保留乘法器,远由于普通的阵列乘法器,这是由于此时将部分分组并分别处理,结果大约能在三级加法器的延迟后得到。
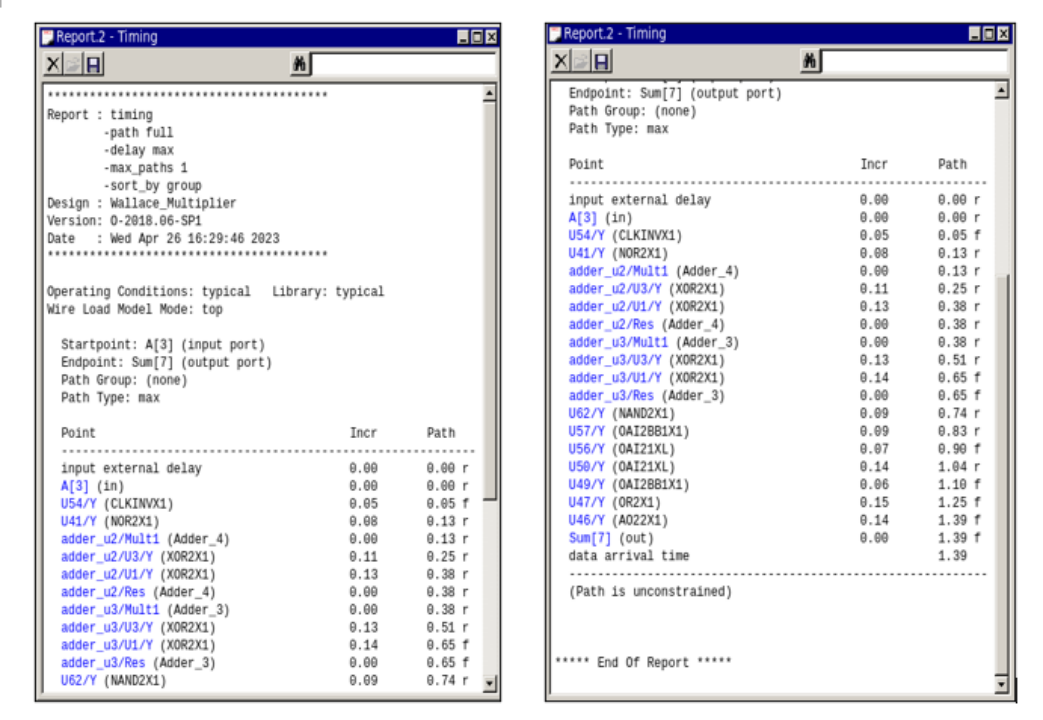 图4 华莱士树乘法器关键路径报告
图4 华莱士树乘法器关键路径报告
在Design Compiler中使用report_area命令,报告所设计电路的面积占用情况,如图5所示,可以看到这个面积略大于阵列乘法器,这是由最后的向量合并加法器贡献的,所以这个面积随着数据位宽的增加不会迅速变大。如果不考虑向量合并加法器的影响,阵列乘法器使用了八个全加器和四个半加器,进位保留乘法器使用了六个全加器和六个半加器,而华莱士树乘法器仅仅用了五个全加器和三个半加器,该实现减少了位宽较大乘法器的硬件开销,同时对传播延时的优化也很显著。
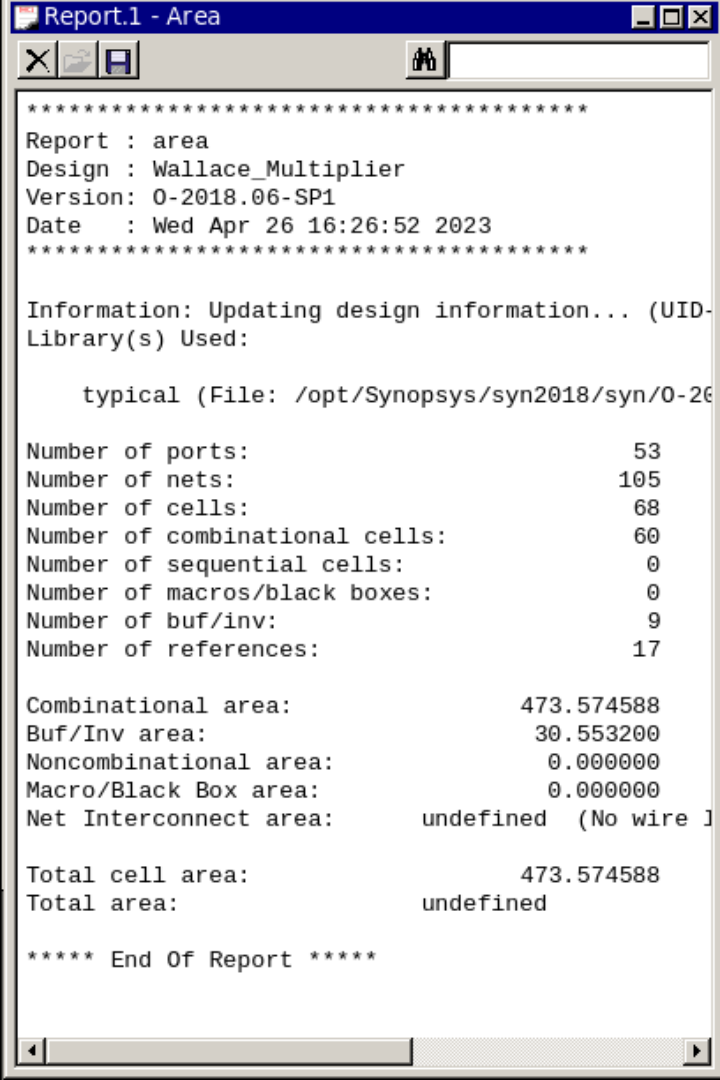
图5 华莱士树乘法器面积报告
进位保留乘法器的Verilog代码如下所示。
module Wallace_Multiplier (input [3:0] A ,input [3:0] B ,output [7:0] Sum
);wire [3:0] partial_product [3:0]; wire [3:0] W_level1_c,W_level1_carry;wire [3:0] W_level2_c,W_level2_carry;assign partial_product[0]=B[0]?A:0;assign partial_product[1]=B[1]?A:0;assign partial_product[2]=B[2]?A:0;assign partial_product[3]=B[3]?A:0;// level1Adder_half adder_half_u1 (.Mult1 (partial_product[0][1]),.Mult2 (partial_product[1][0]),.Res (Sum[1]),.Carry(W_level1_carry[0])); Adder adder_u1 (.Mult1 (partial_product[0][2]),.Mult2 (partial_product[1][1]),.I_carry (partial_product[2][0]),.Res (W_level1_c[1]),.Carry (W_level1_carry[1]));Adder adder_u2 (.Mult1 (partial_product[0][3]),.Mult2 (partial_product[1][2]),.I_carry (partial_product[2][1]),.Res (W_level1_c[2]),.Carry (W_level1_carry[2]));Adder_half adder_half_u2 (.Mult1 (partial_product[1][3]),.Mult2 (partial_product[2][2]),.Res (W_level1_c[3]),.Carry(W_level1_carry[3])); // level2Adder_half adder_half_u3 (.Mult1 (W_level1_c[1]),.Mult2 (W_level1_carry[0]),.Res (Sum[2]),.Carry(W_level2_carry[0])); Adder adder_u3 (.Mult1 (W_level1_c[2]),.Mult2 (W_level1_carry[1]),.I_carry (partial_product[3][0]),.Res (W_level2_c[1]),.Carry (W_level2_carry[1]));Adder adder_u4 (.Mult1 (W_level1_c[3]),.Mult2 (W_level1_carry[2]),.I_carry (partial_product[3][1]),.Res (W_level2_c[2]),.Carry (W_level2_carry[2]));Adder adder_u5 (.Mult1 (W_level1_carry[3]),.Mult2 (partial_product[2][3]),.I_carry (partial_product[3][2]),.Res (W_level2_c[3]),.Carry (W_level2_carry[3]));assign Sum[7:3]={partial_product[3][3],W_level2_c[3:1]}+{W_level2_carry[3:0]};assign Sum[0]=partial_product[0][0];
endmodule相关文章:

数字IC前端学习笔记:数字乘法器的优化设计(华莱士树乘法器)
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 进位保留乘法器依旧保留着阵列的排列规则,只是进位是沿斜下角,如果能使用树形结构来规划这些进位保留加法器,就能获得更短的关键…...

CountDownLatch 批量更改使用,
代码 import com.baomidou.mybatisplus.core.conditions.query.QueryWrapper; import com.baomidou.mybatisplus.extension.service.impl.ServiceImpl; import com.first.pet.platform.entity.PlatformAddress; import com.first.pet.platform.mapper.PlatformAddressMapper; …...
)
910数据结构(2019年真题)
算法设计题 问题1 有一种排序算法叫做计数排序。这种排序算法对一个待排序的表(采用顺序存储)进行排序,并将排序结果存放到另一个新的表中。必须注意的是,表中所有待排序的关键字互不相同,计数排序算法针对表中的每个元素,扫描待排序的表一趟,统计表中有多少个元素的关…...
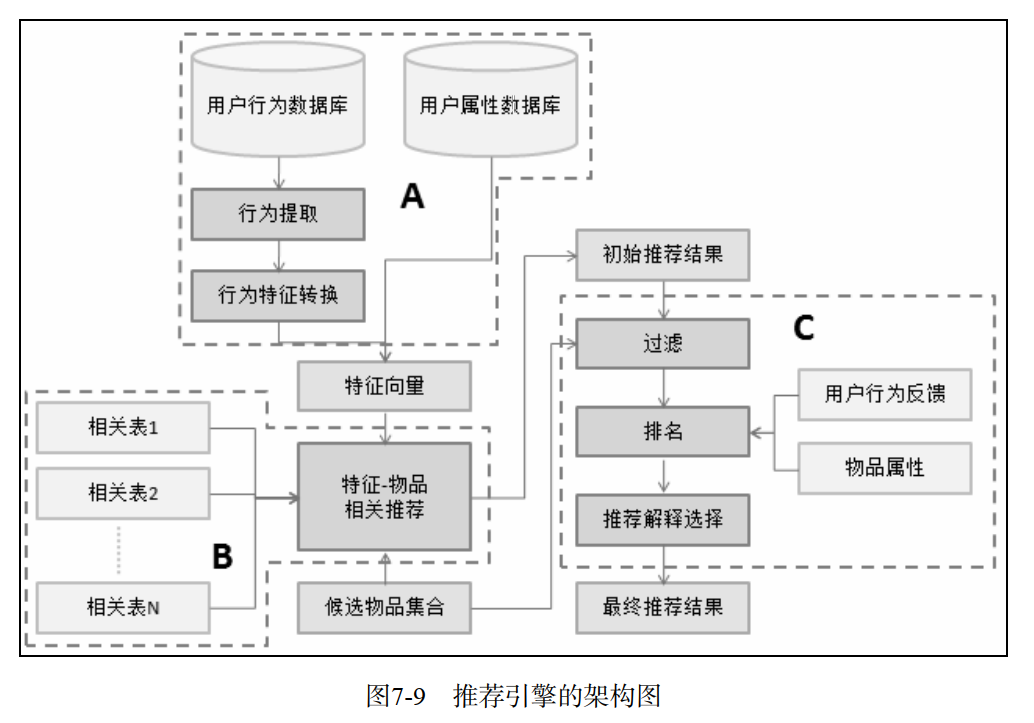
推荐系统实践 笔记
诸神缄默不语-个人CSDN博文目录 这是我2020年写的笔记,我从印象笔记搬过来公开。 如果那年还在读本科的同学也许有印象,那年美赛出了道根据电商评论给商户提建议的题。其实这件事跟推荐系统关系不大,但我们当时病急乱投医,我打开…...

【JavaEE】JUC(Java.util.concurrent)常见类
文章目录 前言ReentrantLock原子类线程池信号量CountDownLatch相关面试题 前言 经过前面文章的学习我们大致了解了如何实现多线程编程和解决多线程编程中遇到的线程不安全问题,java.util.concurrent 是我们多线程编程的一个常用包,那么今天我将为大家分…...

清除浮动的方法
为什么需要清除浮动? 父级的盒子不能把height定死这样,浮动子类就没有了(行内块元素的特点),父类高度为零。故引用清除浮动 1、父级没有高度 2、子盒子浮动了 3、影响下面的布局了,我们就应该清除浮动了…...
LangChain 摘要 和问答示例
在Azure上的OpenAI端点 注意 OpenAI key 可以用微软 用例【1. 嵌入 ,2. 问答】 1. import os import openai from langchain.embeddings import OpenAIEmbeddings os.environ["OPENAI_API_KEY"] "****" # Azure 的密钥 os.environ["OP…...

(32)测距仪(声纳、激光雷达、深度摄影机)
文章目录 前言 32.1 单向测距仪 32.2 全向性近距离测距仪 32.3 基于视觉的传感器 前言 旋翼飞机/固定翼/无人车支持多种不同的测距仪,包括激光雷达(使用激光或红外线光束进行距离测量)、360 度激光雷达(可探测多个方向的障碍…...
教你拥有一个自己的QQ机器人!0基础超详细保姆级教学!基于NoneBot2 Windows端搭建QQ机器人
0.序言 原文链接:教你本地化部署一个QQ机器人本教程主要面向Windows系统用户教程从0开始全程详细指导,0基础萌新请放心食用🍕如果你遇到了问题,请仔细检查是否哪一步有遗漏。如果你确定自己的操作没问题,可以到原文链…...

智能银行卡明细筛选与统计,轻松掌握账户总花销!
作为现代生活的重要组成部分,银行卡成为了我们日常消费和收入的主要途径。但是,当我们需要了解自己的银行卡账户的总花销时,繁琐的明细筛选和统计工作常常让人头疼。现在,让我们向您推荐一款智能银行卡明细筛选与统计工具…...
SRT服务器SLS
目前互联网上的视频直播有两种,一种是基于RTMP协议的直播,这种直播方式上行推流使用RTMP协议,下行播放使用RTMP,HTTPFLV或者HLS,直播延时一般大于3秒,广泛应用秀场、游戏、赛事和事件直播,满足了…...

Linux 安装 Android SDK
先安装jdk RUN apt-get install default-jdk 参考:http://t.zoukankan.com/braveym-p-6143356.html mkdir -p $HOME/install/android-sdk wget https://dl.google.com/android/repository/commandlinetools-linux-9123335_latest.zip unzip commandlinetools-linu…...
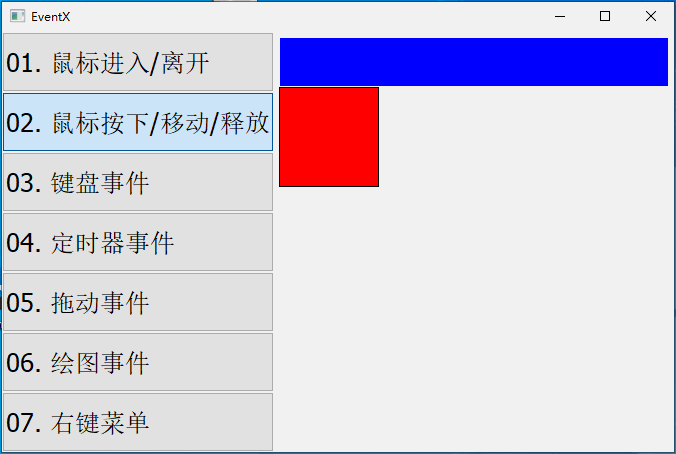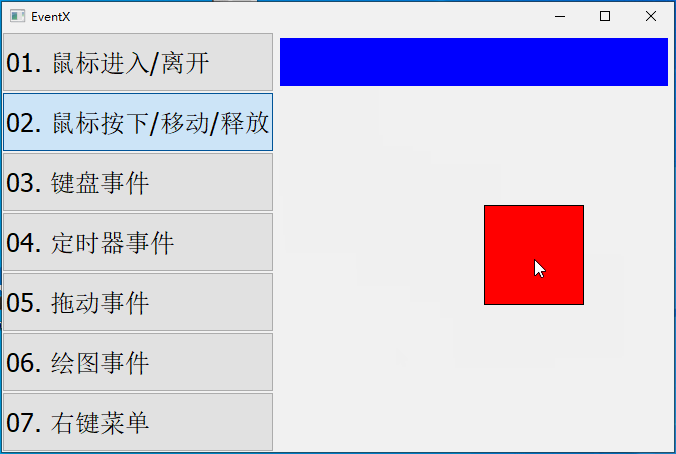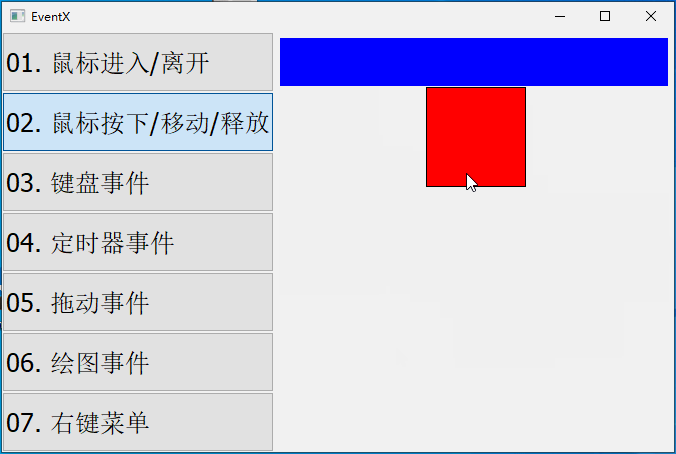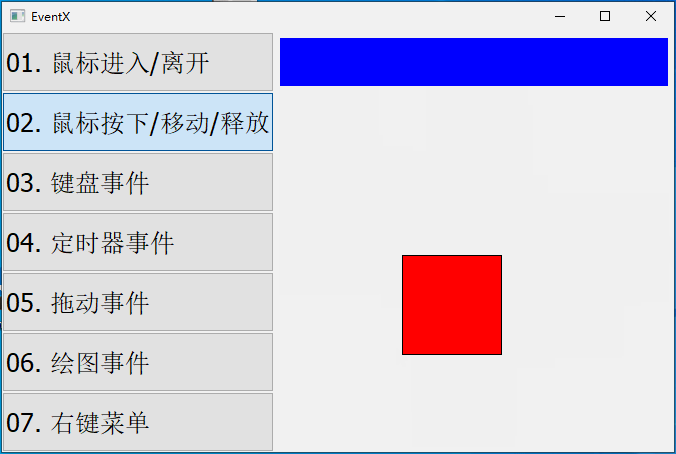
【QT开发笔记-基础篇】| 第四章 事件QEvent | 4.4 鼠标按下、移动、释放事件
本章要实现的整体效果如下: QEvent::MouseButtonPress 鼠标按下时,触发该事件,它对应的子类是 QMouseEvent QEvent::MouseMove 鼠标移动时,触发该事件,它对应的子类是 QMouseEvent QEvent::MouseButtonRel…...

vue3父子通信+ref,toRef,toRefs使用实例
ref是什么? 生成值类型的响应式数据可用于模板和reactive通过.value修改值可以获取DOM元素 <p ref”elemRef”>{{nameRef}} -- {{state.name}}</p> // 获取dom元素 onMounted(()>{ console.log(elemRef.value); }); toRef是什么? 针对一个响应式对象(rea…...
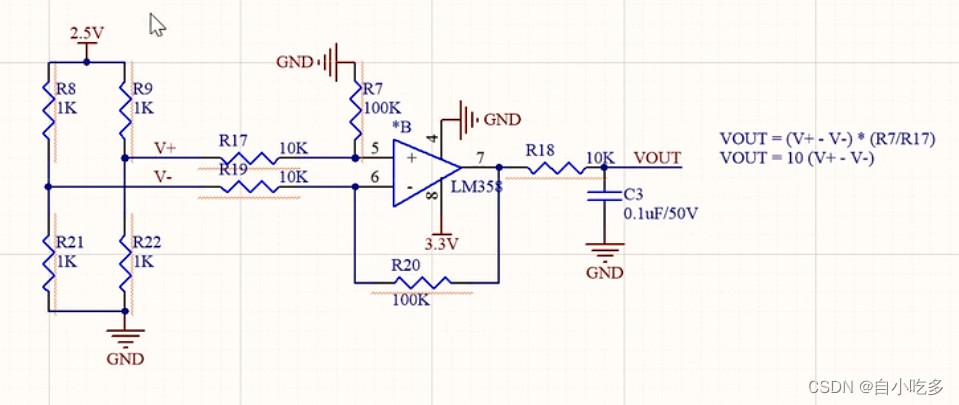
输入电压转化为电流性 5~20mA方案
输入电压转化为电流性 5~20mA方案 方案一方案二方案三 方案一 XTR111是一款精密的电压-电流转换器是最广泛应用之一。原因有二:一是线性度非常好、二是价格便宜。总结成一点,就是性价比高。 典型电路 最终电路 Z1二极管处输出电流表达式:…...
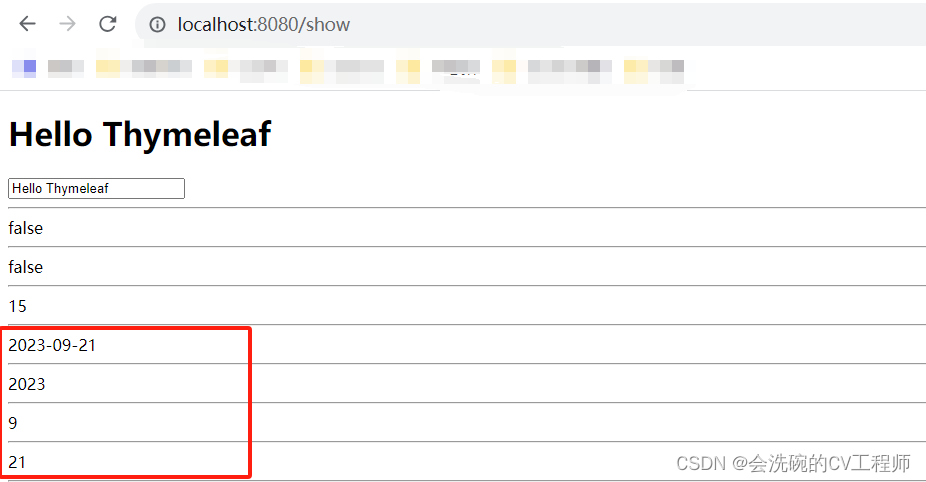
SpringBoot自带模板引擎Thymeleaf使用详解①
目录 前言 一、SpringBoot静态资源相关目录 二、变量输出 2.1 在templates目录下创建视图index.html 2.2 创建对应的Controller 2.3 在视图展示model中的值 三、操作字符串和时间 3.1 操作字符串 3.2 操作时间 前言 Thymeleaf是一款用于渲染XML/HTML5内容的模板引擎&am…...

推荐算法——Apriori算法原理
0、前言: 首先名字别读错:an pu ruo ao rui 【拼音发音】Apriori是一种推荐算法推荐系统:从海量数据中,帮助用户进行信息的过滤和选择。主要推荐方法有:基于内容的推荐、协同过滤推荐、基于关联规则的推荐、基于知识的…...

vue ant 隐藏 列
vue ant 隐藏 列 如果你使用的是Vue和Ant Design Vue组件库,你可以使用v-if指令来实现条件渲染来隐藏列。以下是一个示例代码: <template><a-table :columns"columns" :data-source"data"><template v-slot:custom…...

java基础之初始化顺序
初始化顺序 在类中变量定义的顺序决定了它们初始化的顺序。在创建任何java对象时,都是依次调用父类非静态初始化块、父类构造器执行初始化、本类的非静态初始化块、本类构造器执行初始化 public class House { // 构造器之前 Window w1 new Window(1); Ho…...
FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜)
FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜) FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜)ffmpeg fliter 基本内置变量视频裁剪文字水印图片水印画中画视频多宫格处理 FFmpeg 命…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
