day51【代码随想录】动态规划之回文子串、最长回文子序列
文章目录
- 前言
- 一、回文子串(力扣647)
- 二、最长回文子序列(力扣516)
前言
1、回文子串
2、最长回文子序列
一、回文子串(力扣647)
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串

分析:
1、确定dp[]数组以及下标含义
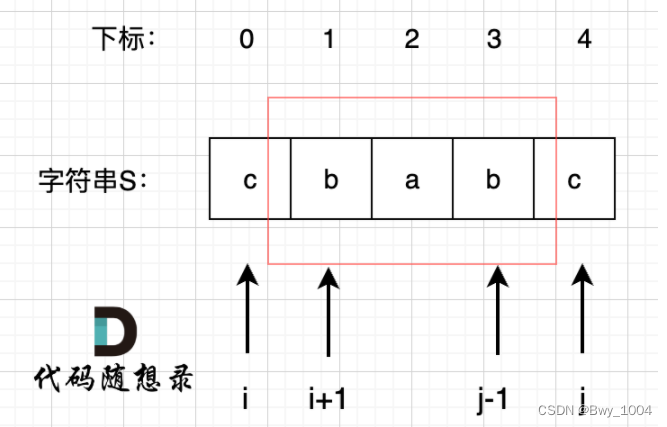
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
2、递推公式
分析两种情况:
s[i]与s[j]相等,s[i]与s[j]不相等两种
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时:
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:i和j仅相差1,“aa” 这样子
情况三:i-j>1 “abccba” 或者 “abca”,此时我们需要判断i-1 和 j+1是不是回文子串,
3、初始化
都初始为false
4、遍历顺序
从下到上
class Solution {public int countSubstrings(String s) {int res = 0;char[] ss = s.toCharArray();if (s == null || (s.length() < 1)) return 0;boolean[][] dp = new boolean[ss.length][ss.length];for(int i=s.length()-1;i>=0;i--){for(int j=i;j<s.length();j++){if(ss[i]==ss[j]){if(Math.abs(i-j)<=1){dp[i][j] = true;res++;}else if(dp[i+1][j-1]==true){dp[i][j] = true;res++;}}else{dp[i][j] = false;}}}return res;}
}

二、最长回文子序列(力扣516)
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。

分析:
回文子串是要连续的,回文子序列可不是连续的!
思路其实是差不多的,但本题要比求回文子串简单一点,因为情况少了一点。
1、确定dp数组以及下标含义
dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串,回文子串的长度最大为dp[i][j]
2、递推公式
分析两种情况:
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
当s[i]与s[j]相等时:
dp[i][j] = dp[i+1][j-1] +2;
3、初始化
在对角线上的情况dp[i][j]应该是初始为1的。即:一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行
4、遍历顺序
从下到上
class Solution {public int longestPalindromeSubseq(String s) {int[][] dp = new int[s.length()][s.length()];if(s==null || s.length()==0) return 0;//初始化for(int i=0;i<s.length();i++){dp[i][i] = 1;}//遍历顺序for(int i=s.length()-2;i>=0;i--){for(int j=i+1;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){dp[i][j] = dp[i+1][j-1]+2;}else{dp[i][j] = Math.max(dp[i][j-1],dp[i+1][j]);}}}return dp[0][s.length()-1];}
}

相关文章:

day51【代码随想录】动态规划之回文子串、最长回文子序列
文章目录前言一、回文子串(力扣647)二、最长回文子序列(力扣516)前言 1、回文子串 2、最长回文子序列 一、回文子串(力扣647) 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目…...
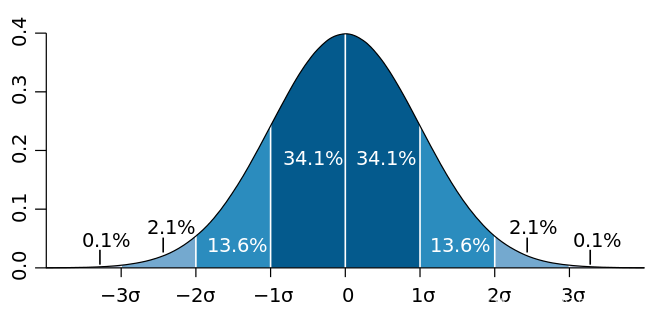
拟凸函数,拟凹函数,单峰函数
拟凸(quasi-convex)函数很早就听说过,但是标准定义一直不太了解,现在总结一下。 一个定义在凸集上的实数函数 fff 是拟凸函数:若对于其定义域内的任意两个点 xxx 和 yyy,以及任意常数 λ∈[0,1]\lambda\in…...
代码:卡尔曼滤波 vs. 卡尔曼平滑)
数据处理(伪)代码:卡尔曼滤波 vs. 卡尔曼平滑
步骤一、导入csv或txt格式的试验数据 最简洁也是据说读取速度最快的方法是: pPath C:\data_org\9#-1.txt % 数据文件 data importdata(pPath); % 读取 pPath 的结果到 一个数据结构变量 data 中。 pData data.data; % 提取有效数据数组data 的数据结构如下&a…...

华为OD机试题,用 Java 解【比赛评分】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

【基础算法】哈希表(开放寻址法)
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
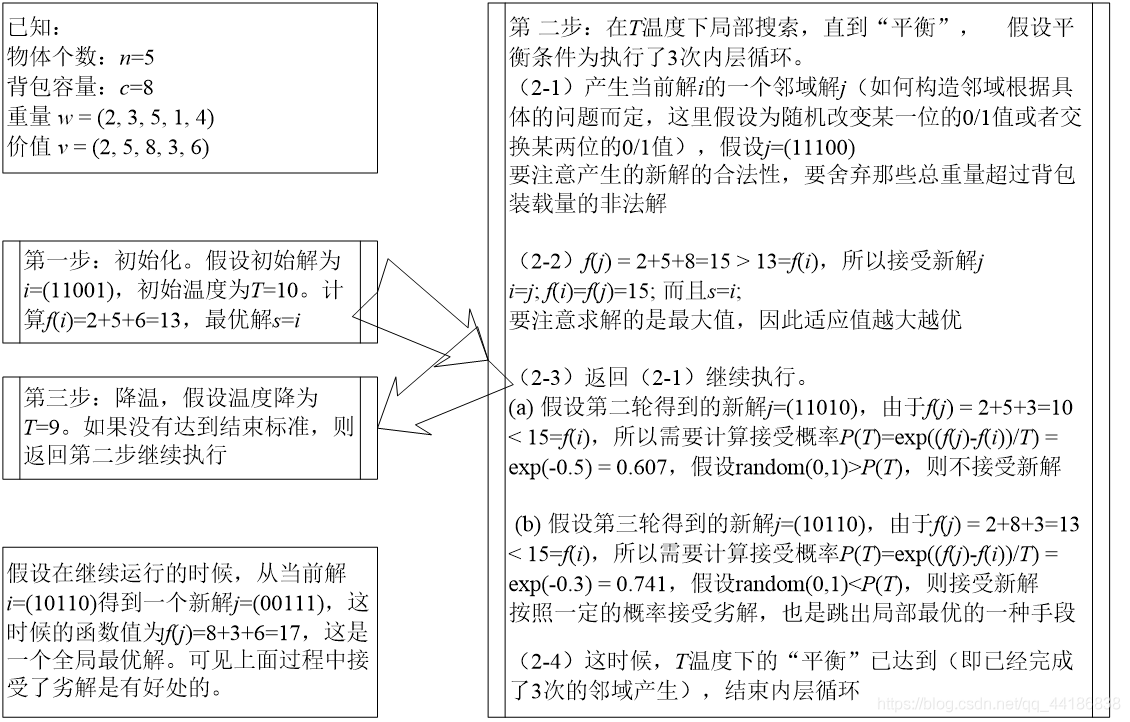
优化算法(寻优问题)
前言 群智能算法(全局最优):模拟退火算法(Simulated annealing,SA),遗传算法(Genetic Algorithm, GA),粒子群算法(Particle Swarm Optimization&…...

基于视频流⽔线的Opencv缺陷检测项⽬
代码链接见文末 1.数据与任务概述 输入为视频数据,我们需要从视频中检测出缺陷,并对缺陷进行分类。 2.整体流程 (1)视频数据读取和轮廓检测 首先,我们需要使用opencv读取视频数据,将彩色图转为灰度图后进行图像阈值处理。阈值处理是为了让前景和背景更明显的区分处理。…...
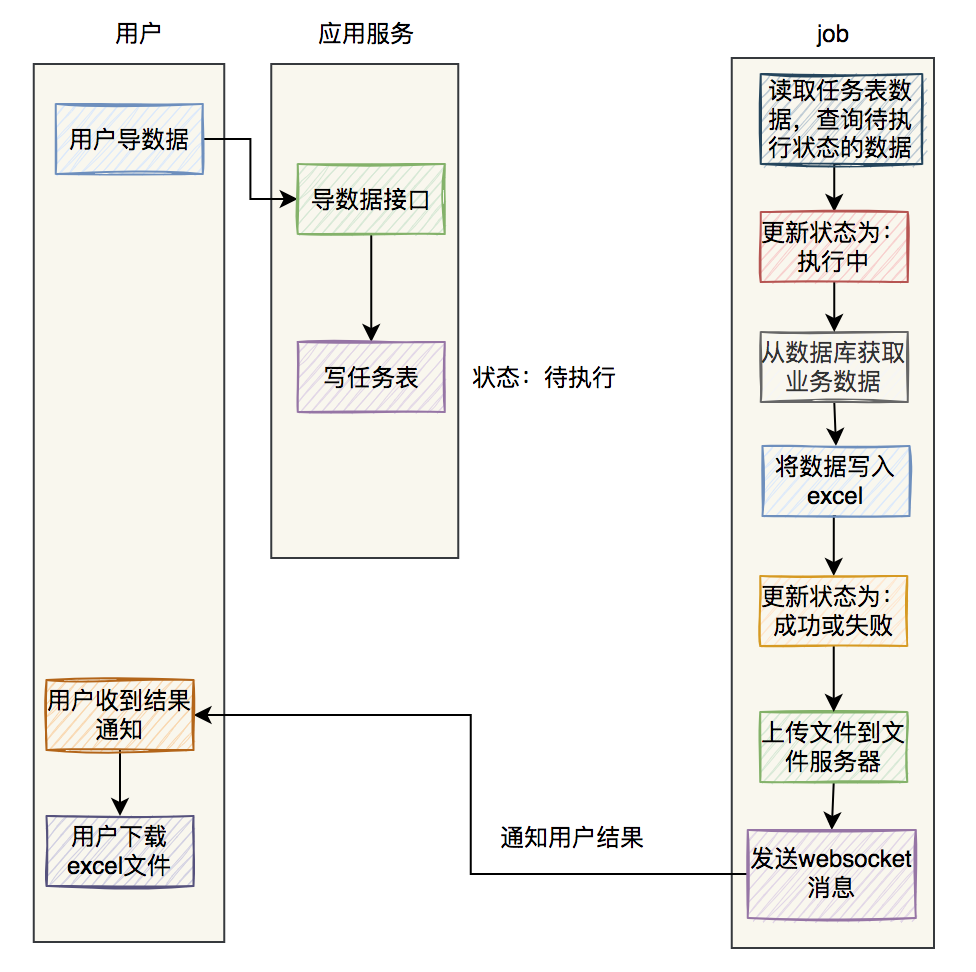
百万数据excel导出功能如何实现?
最近我做过一个MySQL百万级别数据的excel导出功能,已经正常上线使用了。 这个功能挺有意思的,里面需要注意的细节还真不少,现在拿出来跟大家分享一下,希望对你会有所帮助。 原始需求:用户在UI界面上点击全部导出按钮…...

华为OD机试题,用 Java 解【合规数组】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...
SAP ABAP中的数据类型 Data Types
简单来说分两种: 数据字典里定义的在ABAP程序里定义的 文章目录1. ABAP数据字典里的1.1 数字型的1.2 字符型1.3 字节型1.4 特殊类型2. 预定义的ABAP数据类型2.1 预定义数字型2.2 预定义字符型2.3 预定义字节型1. ABAP数据字典里的 1.1 数字型的 用在数学计算里的…...
HashMap~
HashMap: HashMap是面试中经常被问到的一个内容,以下两个经常被问到的问题, Question1:底层数据结构,1.7和1.8有何不同? 答:1.7数组+链表,1.8数组+(链表|红…...
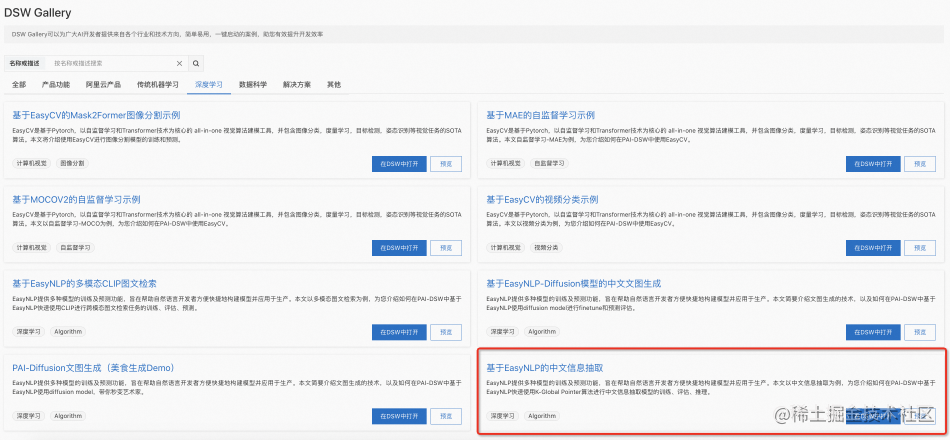
EasyNLP集成K-Global Pointer算法,支持中文信息抽取
作者:周纪咏、汪诚愚、严俊冰、黄俊 导读 信息抽取的三大任务是命名实体识别、关系抽取、事件抽取。命名实体识别是指识别文本中具有特定意义的实体,包括人名、地名、机构名、专有名词等;关系抽取是指识别文本中实体之间的关系;…...

mysql lesson3
DQL查找语句续集.............................. 分组函数(也叫多行处理函数) 1: select sum(sal) from emp;select min(sal)from emp;select max(sal)from emp;select avg(sal)from emp;select count(ename)from emp;2:分组函…...
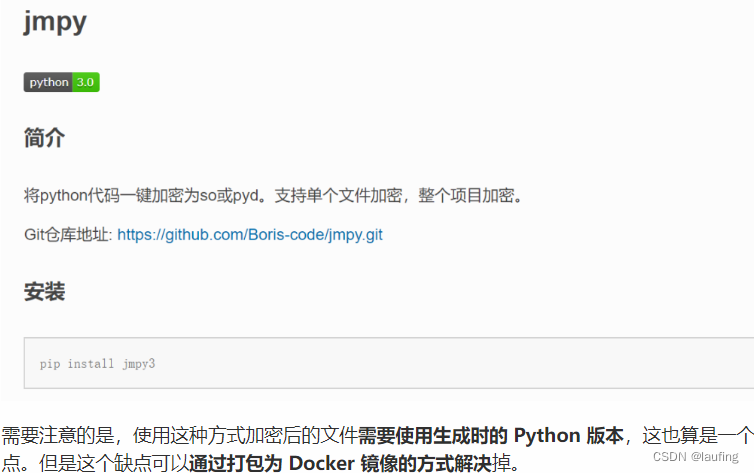
python源码保护
文章目录代码混淆打包exe编译为字节码源码加密项目发布部署时,为防止python源码泄漏,可以通过几种方式进行处理代码混淆 修改函数、变量名 打包exe 通过pyinstaller 将项目打包为exe可执行程序,不过容易被反编译。 编译为字节码 py_comp…...

第51讲:SQL优化之COUNT查询的优化
文章目录 1.COUNT查询优化的概念2.COUNT函数的用法1.COUNT查询优化的概念 在很多的业务场景下可能需要统计一张表中的总数据量,当表的数据量很大时,使用COUNT统计表数据量时,也是非常耗时的。 MyISAM引擎会把一个表的总行记录在磁盘中,当执行count(*)的时候会直接从磁盘中…...

ArrayBlockingQueue
同步队列超出长度时,不同的返回形式可以分为以下四种。 会抛异常不会抛异常,有返回值死等,直到可以插入值或者取到值设置等待超时时间添加方法add()offfer()put()offer(E e,long timeout, TimeUnit unit)删除方法remove()poll()take()poll(l…...

DeepLabV3+:对预测处理的详解
相信大家对于这一部分才是最感兴趣的,能够实实在在的看到效果。这里我们就只需要两个.py文件(deeplab.py、predict_img.py)。 创建DeeplabV3类 deeplab.py的作用是为了创建一个DeeplabV3类,提供一个检测图片的方法,而…...
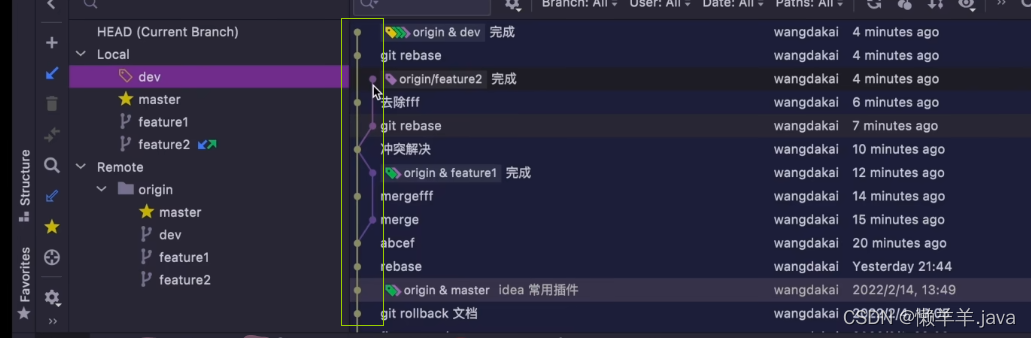
【Git】与“三年经验”就差个分支操作的距离
前言 Java之父于胜军说过,曾经一位“三年开发经验”的程序员粉丝朋友,刚入职因为不会解决分支问题而被开除,这是不是在警示我们什么呢? 针对一些Git的不常用操作,我们通过例子来演示一遍 1.版本回退 1.1已提交但未p…...
【经验】win10设置自启动
方法一:自启动文件夹 按下winr快捷键,弹出运行窗口,输入:shell:startup,弹出自启动文件夹窗口,将要开机自启的程序或快捷方式复制到此窗口中即可。 自启动文件夹路径:C:\Users\【用户名】\Ap…...

Linux SPI-NAND 驱动开发指南
文章目录Linux SPI-NAND 驱动开发指南1 概述1.1 编写目的1.2 适用范围1.3 相关人员3 流程设计3.1 体系结构3.2 源码结构3.3 关键数据定义3.3.1 flash 设备信息数据结构3.3.2 flash chip 数据结构3.3.3 aw_spinand_chip_request3.3.4 ubi_ec_hdr3.3.5 ubi_vid_hdr3.4 关键接口说…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
