基于LADRC自抗扰控制的VSG三相逆变器预同步并网控制策略(Simulink仿真实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 整体控制框图
2.2 主体仿真模型
2.3 主体控制模块
2.4 有功无功比较图
2.5 使用普通VSG控制的并网电压波形图
2.6 使用LADRC后的VSG逆变器并网电压波形
2.7 并网电流谐波分析
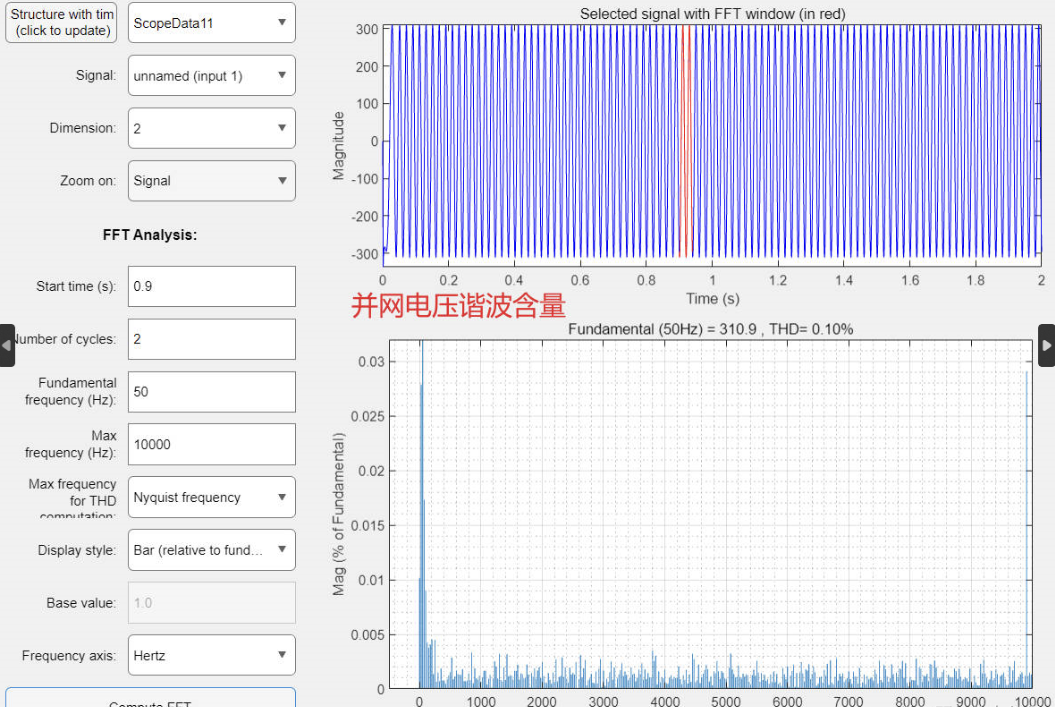
2.8 并网电压谐波分析
🎉3 参考文献
🌈4 Simulink仿真实现
💥1 概述
基于LADRC自抗扰控制的VSG三相逆变器预同步并网控制策略是一种用于实现逆变器在微电网中的协调运行的先进控制策略。
逆变器控制方式采用虚拟同步发电机控制(VSG),通过引入虚拟同步发电机的概念,为逆变器系统提供了类似于实际同步发电机的惯性和阻尼支撑。这种控制方式能够有效提高逆变器系统的稳定性和响应速度,使其更好地适应微电网的运行要求。
为了增强逆变器系统的鲁邦性和抗扰能力,本模型采用了LADRC自抗扰控制。LADRC(Linear Active Disturbance Rejection Control)是一种先进的控制算法,能够有效抑制系统中的各种干扰和扰动,并实现对系统动态特性的精确控制。通过采用LADRC自抗扰控制,逆变器系统能够在面对外部干扰和系统参数变化时保持较高的稳定性和鲁邦性。
在并网过程中,为了减小逆变器并网时产生的冲击电流对系统的影响,采用了预同步控制策略。预同步控制是一种先行控制策略,通过提前调节逆变器输出电压和频率,使其与微电网的电压和频率趋于一致,从而减小并网时的电流冲击。这种控制策略能够有效保护微电网中其他逆变器和负载设备的稳定运行,提高整体并网效率。
除了上述控制策略,系统频率变化曲线是评估逆变器运行性能的重要指标。通过对系统频率变化曲线的分析,可以了解逆变器在并网过程中的频率响应特性,判断其稳定性和准确性。频率变化曲线的平稳性和快速响应性是评估逆变器控制策略优劣的重要依据。
综上所述,基于LADRC自抗扰控制的VSG三相逆变器预同步并网控制策略在微电网中具有重要的应用价值。通过引入虚拟同步发电机控制、采用LADRC自抗扰控制和预同步控制策略,逆变器系统能够实现更高的稳定性、鲁邦性和并网效率,为微电网的可靠运行提供了有效的支持。同时,通过对系统频率变化曲线的分析,能够全面评估逆变器控制策略的性能,并进一步优化和改进。
📚2 运行结果
2.1 整体控制框图
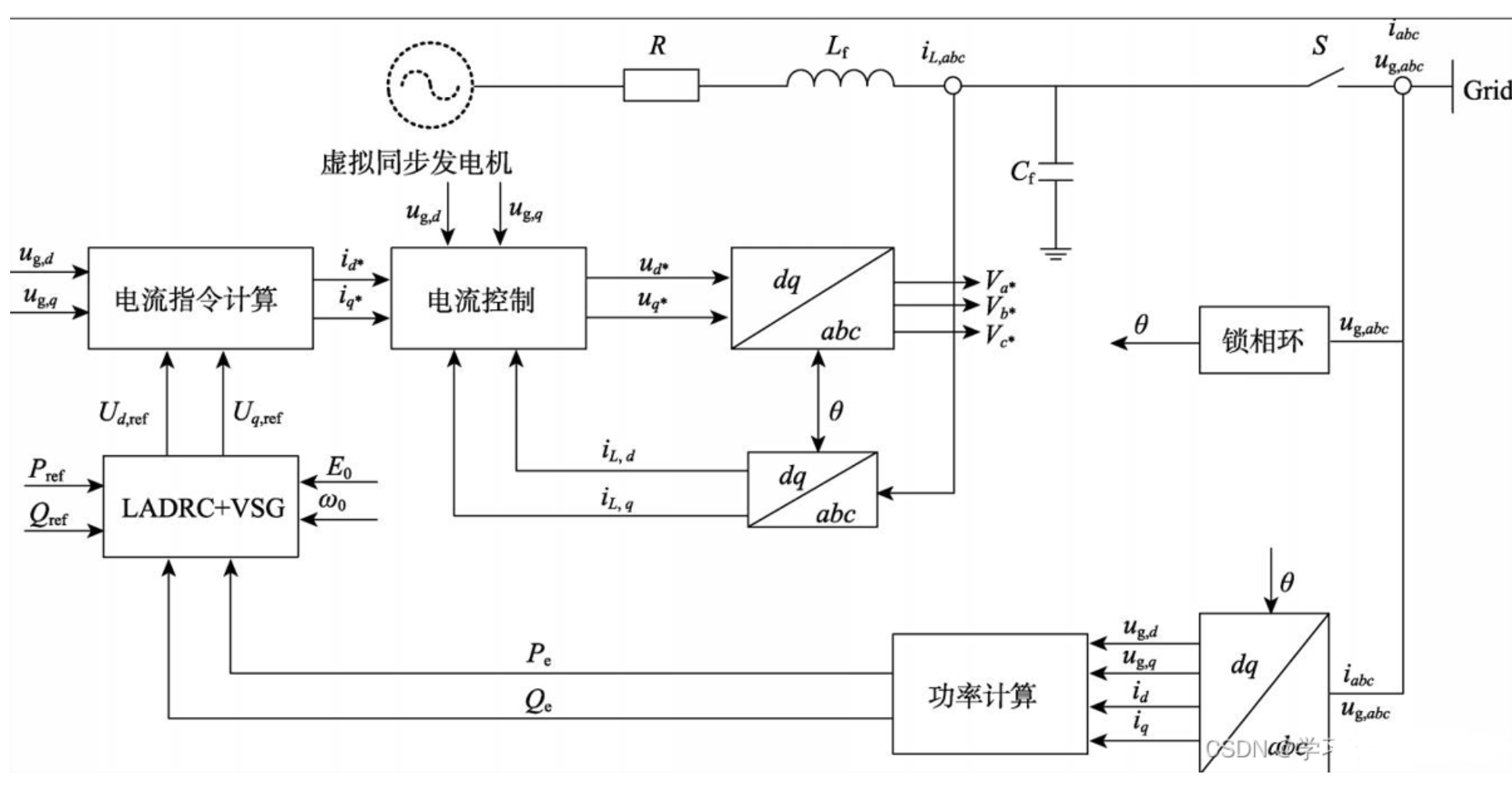
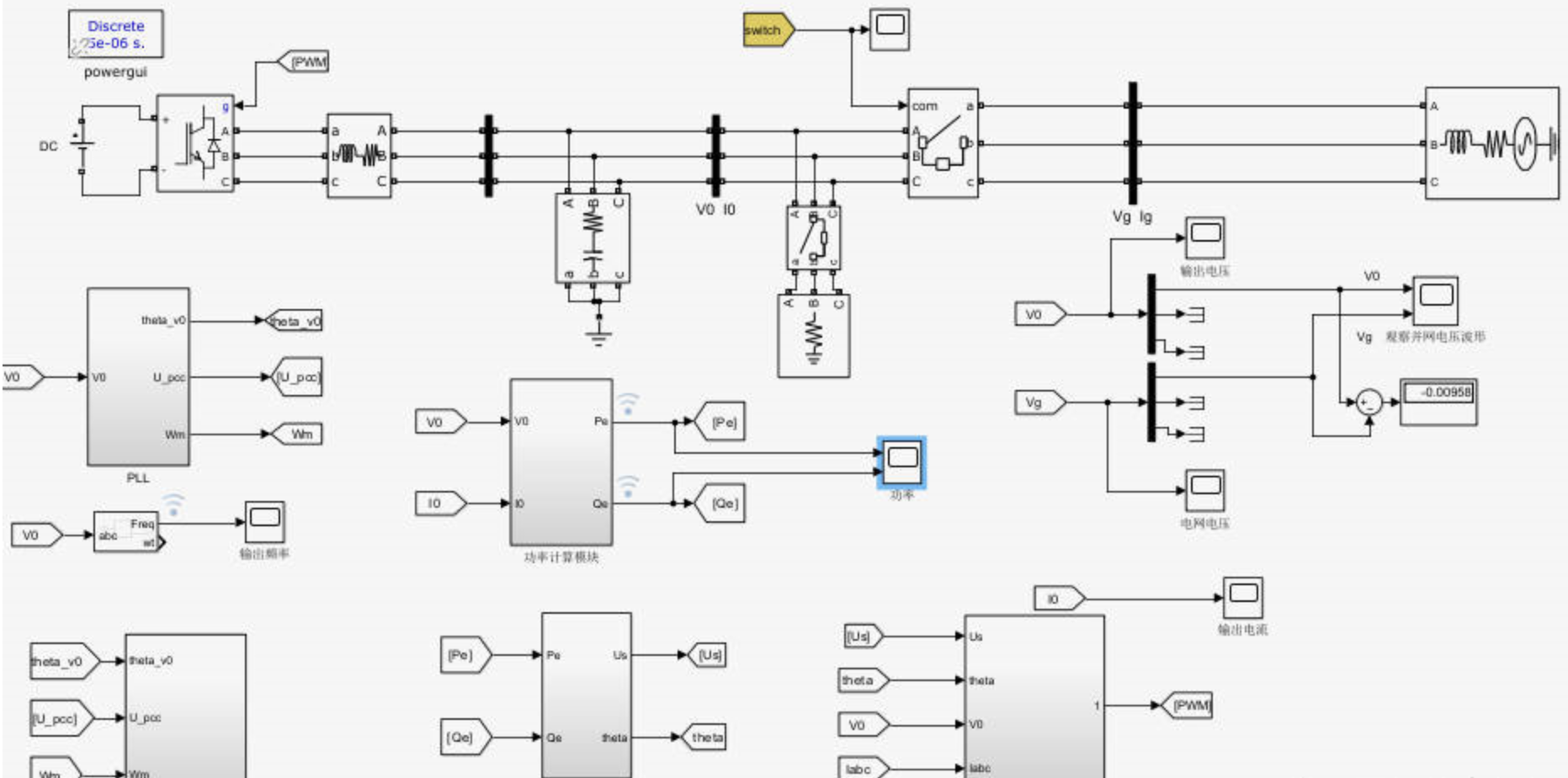
2.2 主体仿真模型
功率计算模块、锁相环模块、虚拟同步机控制模块、自抗扰控制模块、电压电流环控制模块(三相准PR控制)、PWM模块。
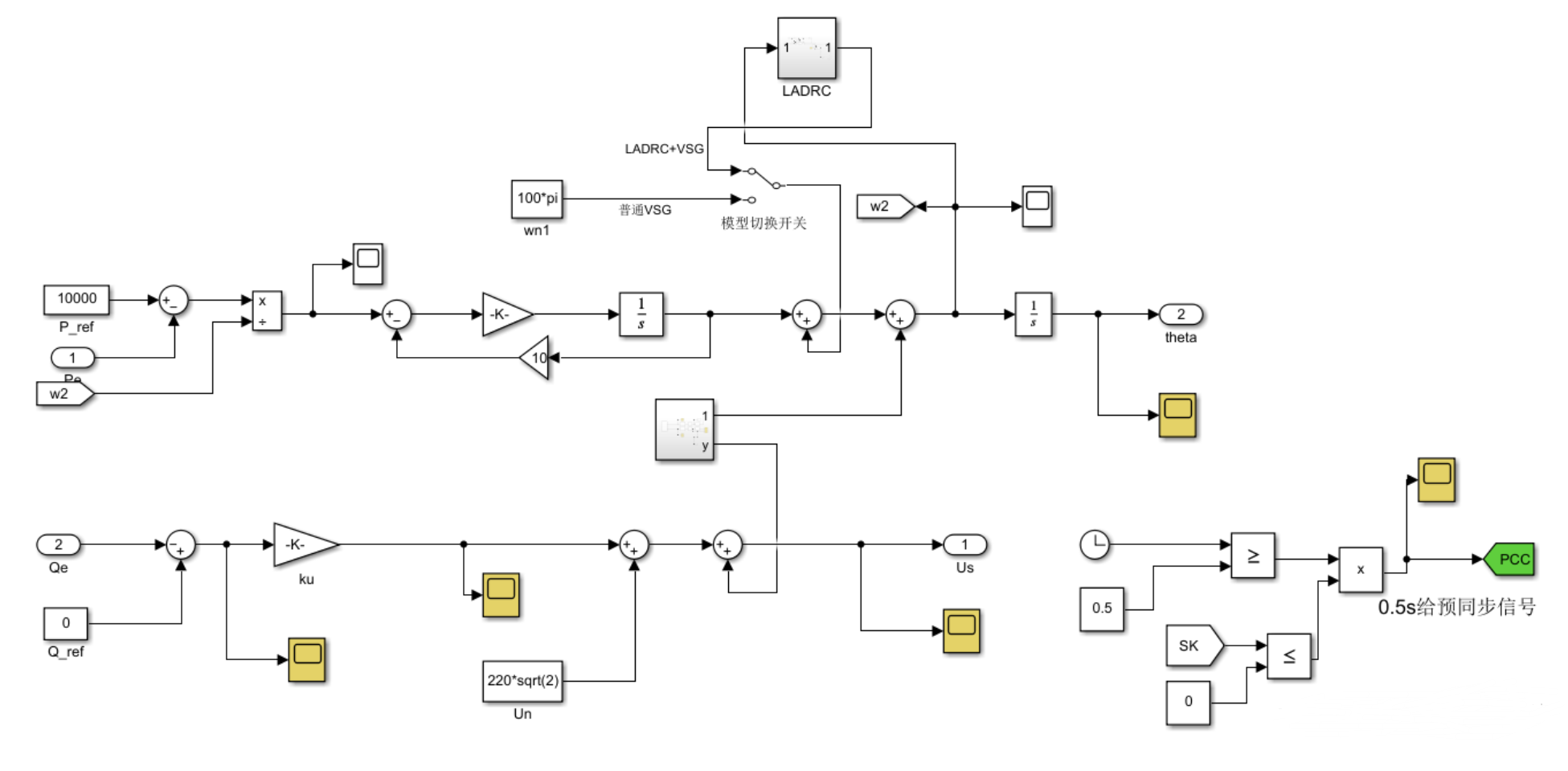
2.3 主体控制模块
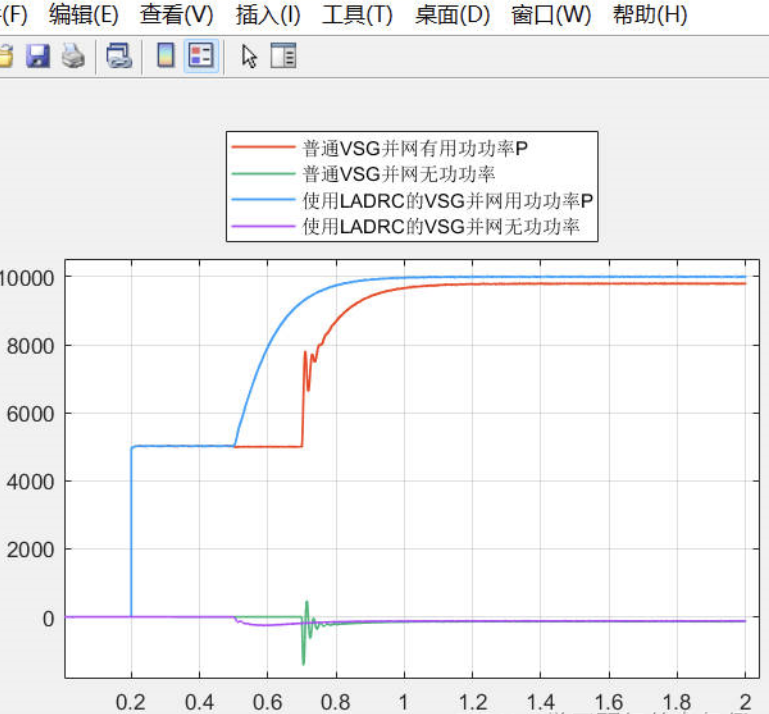
2.4 有功无功比较图
2.5 使用普通VSG控制的并网电压波形图

2.6 使用LADRC后的VSG逆变器并网电压波形
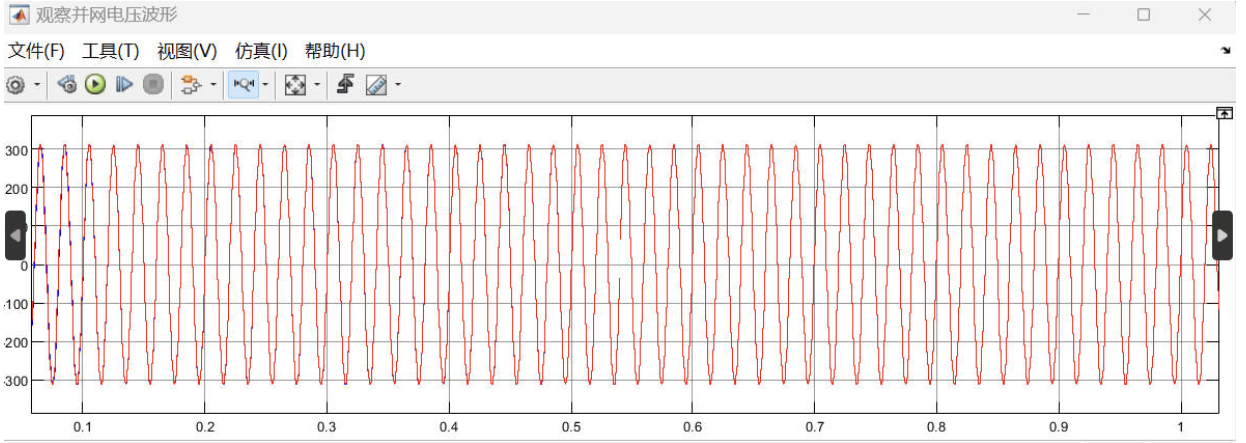
图为普通vsg逆变器骅网时a相和电网a相电压跟随图,下图为加入LADRC后的vsg逆变器并网图,加入LADRC后能在很早时候就保持同步,更有利于并网.
2.7 并网电流谐波分析
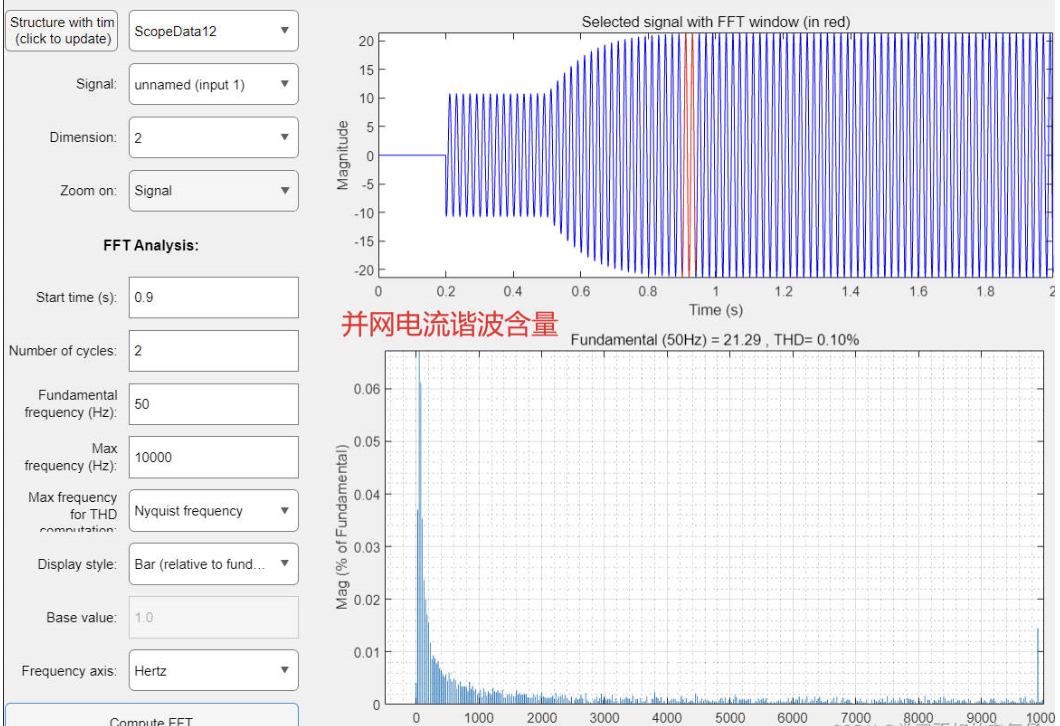
2.8 并网电压谐波分析
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]涂丹凤,张代润,范文,等.基于VSG的并网变流器LADRC策略研究[J].电测与仪表, 2022(007):059.
[2]梁文科,苏淑靖,梁东飞,等.两相静止坐标系下并网逆变器的自抗扰控制[J].电子测量技术, 2022, 45(10):7.
[3]凌毓畅,曾江.LCL型并网逆变器的线性自抗扰控制[J].电气传动, 2018, 48(9):8.DOI:10.19457/j.1001-2095.dqcd18034.
[4]魏久林,王奔,段瑞林,等.基于VSG并网逆变器的模糊滑模控制策略研究[J].电工技术, 2019(15):6.DOI:CNKI:SUN:DGJY.0.2019-15-011.
🌈4 Simulink仿真实现
相关文章:

基于LADRC自抗扰控制的VSG三相逆变器预同步并网控制策略(Simulink仿真实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

[0xGame 2023] week1
整理一下,昨天该第二周了。今天应该9点结束提交,等我写完就到了。 PWN 找不到且不对劲的flag 第1题是个nc测试,但也不完全是,因为flag在隐含目录里 高端的syscall 程序使用了危险函数,并且没有canary阻止࿰…...

Matlab矩阵——矩阵行列互换
问题:如何将 1*n 的矩阵转换为指定 M*N 的矩阵,或者将 M*N 的矩阵转换为 1*n 的矩阵? 处理方法:使用 reshape 函数进行矩阵的行列互换 分两种情况如下: 一、将 1*n 的矩阵转换为指定 M*N 的矩阵 假如有4个坐标值&a…...

OpenMesh 网格面片随机赋色
文章目录 一、简介二、实现代码三、实现效果一、简介 OpenMesh中的赋色方式与Easy3D很是类似,它统一有一个属性数组来进行管理,我们在进行赋色等操作时,必须要首先添加该属性才能进行使用,这里也进行记录一下(法向量等特征也是类似的操作)。 二、实现代码 #define _USE_…...
SpringSecurity源码学习一:过滤器执行原理
目录 1. web过滤器Filter1.1 filter核心类1.2 GenericFilterBean1.3 DelegatingFilterProxy1.3.1 原理1.3.2 DelegatingFilterProxy源码 2. FilterChainProxy源码学习2.1 源码2.1.1 doFilterInternal方法源码2.1.1.1 getFilters()方法源码2.1.1.2 VirtualFilterChain方法源码 3…...
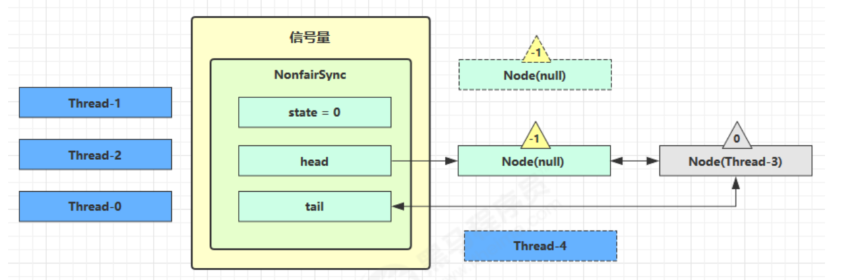
8.2 JUC - 4.Semaphore
目录 一、是什么?二、简单使用三、semaphore应用四、Semaphore原理 一、是什么? Semaphore:信号量,用来限制能同时访问共享资源的线程上限 二、简单使用 public class TestSemaphore {public static void main(String[] args) …...

前端try和catch
为什么要使用try catch 使用try...catch语句是为了处理和管理可能会在程序运行过程中发生的异常或错误情况。以下是一些使用try...catch的主要原因: 错误处理:在开发过程中,无法避免地会出现各种错误,如网络请求失败、数据解析错误…...

Unity可视化Shader工具ASE介绍——2、ASE的Shader创建和输入输出
大家好,我是阿赵,这里继续介绍Unity可视化写Shader的ASE插件的用法。上一篇介绍了ASE的安装和编辑器界面分布,这一篇主要是通过一个简单的例子介绍shader的创建和输入输出。 一、ASE的Shader创建 这里先选择Surface类型的Shader,…...
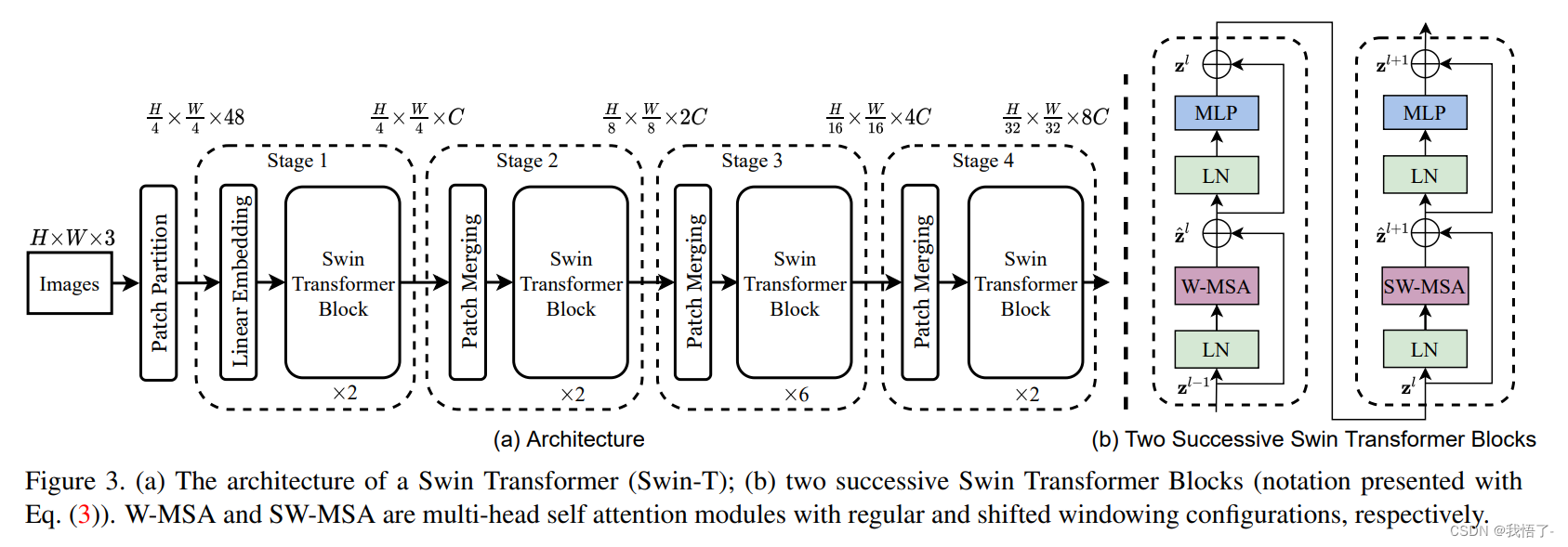
目标检测算法改进系列之Backbone替换为Swin Transformer
Swin Transformer简介 《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》作为2021 ICCV最佳论文,屠榜了各大CV任务,性能优于DeiT、ViT和EfficientNet等主干网络,已经替代经典的CNN架构,成为了计算机…...
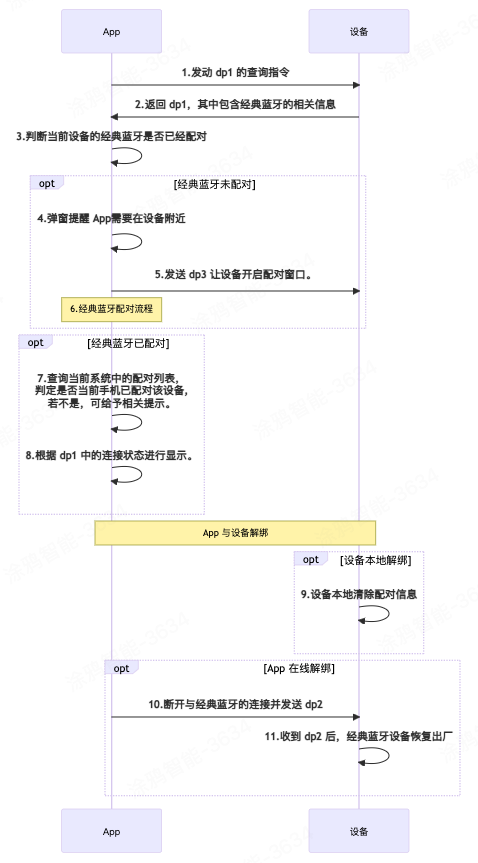
【技术干货】如何通过 DP 实现支持经典蓝牙的联网单品设备与 App 配对
经典蓝牙模块(Classic Bluetooth)主要用于呼叫和音频传输,所以经典蓝牙最主要的特点就是功耗大,传输数据量大。蓝牙耳机、蓝牙音箱等场景大多采用经典蓝牙,因为蓝牙是为传输声音而设计的,是短距离音频传输的…...

【Unity Build-In管线的SurfaceShader剖析_PBS光照函数】
Unity Build-In管线的SurfaceShader剖析 在Unity Build-In 管线(Universal Render Pipeline)新建一个Standard Surface Shader文件里的代码如下:选中"MyPBR.Shader",在Inspector面板,打开"Show generat…...

thinkphp5实现ajax图片上传,压缩保存到服务器
<div class"warp"><input type"file" id"file" accept"image/*" onchange"upimg(this)" /></div> <img src"" /> <script>//上传图片方法function upimg(obj){var fileData obj.…...
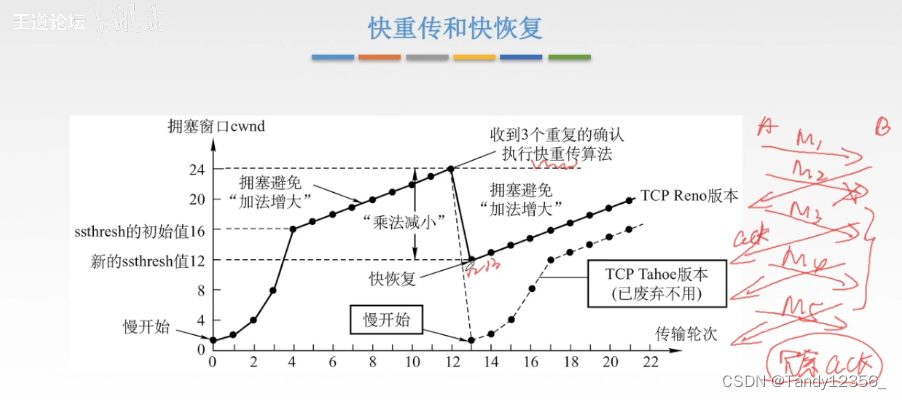
王道考研计算机网络——传输层
一、传输层概述 复用:发送方不同的应用进程都可以使用同一个传输层的协议来传送数据 分用:接收方的传输层在去除报文段的首部之后能把数据交给正确的应用进程 熟知端口号就是知名端口号0-1023 客户端使用的端口号是动态变化的,不是唯一确定…...
)
08 集群参数配置(下)
Kafka Broker不需要太大的堆内存? Kafka Broker不需要太大的堆内存?应该把内存留给页缓存使用? kafka刷盘时宕机 kafka认为写入成功是指写入页缓存成功还是数据刷到磁盘成功算成功呢?还是上次刷盘宕机失败的问题,页…...
mac文件为什么不能拖进U盘?
对于Mac用户来说,可能会遭遇一些烦恼,比如在试图将文件从Mac电脑拖入U盘时,却发现文件无法成功传输。这无疑给用户带来了很大的不便。那么,mac文件为什么不能拖进U盘,看完这篇你就知道了。 一、U盘的读写权限问题 如果…...

RK3568的CAN驱动适配
目录 背景: 1.内核驱动模块配置 2.设备树配置 3.功能测试 4.bug修复 背景: 某个项目上使用RK3568的芯片,需要用到4路CAN接口进行通信,经过方案评审后决定使用RK3568自带的3路CAN外加一路spi转的CAN实现功能,在这个…...

Opengl之立方体贴图
简单来说,立方体贴图就是一个包含了6个2D纹理的纹理,每个2D纹理都组成了立方体的一个面:一个有纹理的立方体。你可能会奇怪,这样一个立方体有什么用途呢?为什么要把6张纹理合并到一张纹理中,而不是直接使用6个单独的纹理呢?立方体贴图有一个非常有用的特性,它可以通过一…...

EF Core报错:Error Number:-2146893019
appsettings.json中的连接字符串要添加上:TrustServerCertificatetrue; 所以这里的连接字符串为:Data SourceLAPTOP-61GDB2Q7\\SQLEXPRESS;Initial CatalogMvcMovie.Data;Persist Security InfoTrue;TrustServerCertificatetrue;User IDsa;Passwordroot…...
QT之可自由折叠和展开的布局
介绍和功能分析 主要是实现控件的折叠和展开,类似抽屉控件,目前Qt自带的控件QToolBox具有这个功能,但是一次只能展开一个,所以针对自己的需求可以自己写一个类似的功能,这里实现的方法比较多,其实原理也比较…...
数组指定元素求和)
javascript二维数组(7)数组指定元素求和
项目需求 对指定数据中的score求和 const data [ { name: Alice, age: 23, score: 85 }, { name: Bob, age: 30, score: 90 }, { name: Charlie, age: 35, score: 80 } ];1.封装函数 这个函数接受两个参数:一个对象数组和一个键名(也就是你想要…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...

[特殊字符] Spring Boot底层原理深度解析与高级面试题精析
一、Spring Boot底层原理详解 Spring Boot的核心设计哲学是约定优于配置和自动装配,通过简化传统Spring应用的初始化和配置流程,显著提升开发效率。其底层原理可拆解为以下核心机制: 自动装配(Auto-Configuration) 核…...

IP选择注意事项
IP选择注意事项 MTP、FTP、EFUSE、EMEMORY选择时,需要考虑以下参数,然后确定后选择IP。 容量工作电压范围温度范围擦除、烧写速度/耗时读取所有bit的时间待机功耗擦写、烧写功耗面积所需要的mask layer...

