【群智能算法改进】一种改进的光学显微镜算法 IOMA算法[1]【Matlab代码#60】
文章目录
- 【`获取资源`请见文章第5节:资源获取】
- 1. 光学显微镜算法(OMA)
- 1.1 物镜放大倍数
- 1.2 目镜放大倍数
- 2. 改进后的IOMA算法
- 2.1 透镜成像折射方向学习
- 3. 部分代码展示
- 4. 仿真结果展示
- 5. 资源获取说明
【获取资源请见文章第5节:资源获取】
1. 光学显微镜算法(OMA)
光学显微镜算法(Optical Microscope Algorithm,OMA)是受显微镜放大倍数启发的一种新的元启发式算法,可用于解决工程优化问题。
新颖的 OMA 具有鲁棒性、易于实现且使用较少控制参数的特点,可用于解决各种数值优化问题。
OMA 是一种基于物理的算法,它模拟观察者放大物体的过程,从观察者的眼睛开始,然后通过显微镜镜头。OMA用于获得最佳目标对象的四步过程如下图所示。

1.1 物镜放大倍数
该算法中目标物体的放大倍数遵循复合显微镜使用的放大原理,并使用公式(1)进行建模。
M t o t a l = M O ∗ M E (1) M_{total}=M_{O}*M_{E}\tag1 Mtotal=MO∗ME(1)
其中, M t o t a l M_{total} Mtotal代表显微镜的总视觉放大倍数, M O M_{O} MO是物镜的放大倍数, M E M_{E} ME并且是目镜的放大倍数。物镜的放大倍率方程一般用用公式(2)表示:
M O = L f 0 (2) M_{O}=\frac{L}{f_{0}}\tag2 MO=f0L(2)
其中, L L L是显微镜的镜筒长度, f 0 f_{0} f0是物镜的焦距。要计算这两个值,需要从最佳目标对象的位置进行参考( M b e s t M_{best} Mbest),用物镜放大。
修改后的目标对象 M i , n e w M_{i,new} Mi,new的数学表达式为:
M i , n e w = M i + m r ∗ 1.40 ∗ M b e s t (3) M_{i,new}=M_{i}+m^{r}*1.40*M_{best}\tag3 Mi,new=Mi+mr∗1.40∗Mbest(3)
修改后的目标对象( M i , n e w M_{i,new} Mi,new)然后与当前物体进行比较,选择两者中较好的一个作为最佳放大倍数。
1.2 目镜放大倍数
显微镜的第二个透镜是目镜,它是继物镜之后用来放大物体的。目镜的放大倍率方程一般用公式(4)表示:
M O = D f e (4) M_{O}=\frac{D}{f_{e}}\tag4 MO=feD(4)
其中, D D D是最短视觉距离, f e f_{e} fe并且是目镜的焦距。目镜阶段是高级放大倍率的更具体的阶段。因此,为了确定两者的长度,需要从用目镜放大的局部搜索空间的距离作为参考。
为了模拟目镜的放大效果,根据所选目标物体之间的距离确定放大空间( i i i)和群体中的另一个目标对象( j j j)。目标对象( i i i)被随机选择来计算局部搜索空间。
这种修改后的放大倍数被认为是对本地搜索空间的有效利用。公式(5)和(6)分别用于模拟目标物体的放大和修改模式。
s p a c e = { M j − M i , i f f ( M i ) > = f ( M j ) M i − M j , i f f ( M i ) < f ( M j ) (5) space=\left\{\begin{matrix}M_{j}-M_{i},\quad if \quad f(M_{i})>=f(M_{j}) \\M_{i}-M_{j},\quad if \quad f(M_{i})<f(M_{j}) \end{matrix}\right.\tag5 space={Mj−Mi,iff(Mi)>=f(Mj)Mi−Mj,iff(Mi)<f(Mj)(5)
M i , n e w = M i + m r ∗ 0.55 ∗ s p a c e (6) M_{i,new}=M_{i}+m^{r}*0.55*space\tag6 Mi,new=Mi+mr∗0.55∗space(6)
2. 改进后的IOMA算法
2.1 透镜成像折射方向学习
透镜成像折射反向学习策略的思想来自于凸透镜成像的原理。通过基于当前坐标生成一个反向位置来扩展搜索范围,如图1所示。

在二维坐标中,x轴的搜索范围为(a, b), y轴表示一个凸透镜。假设物体A在x轴上的投影为x,高度为h,通过透镜成像,另一侧的图像为A*, A在x轴上的投影为x,高度为h*。通过以上分析,我们可以得到如下公式:
( a + b ) / 2 − x x ∗ − ( a + b ) / 2 = h h ∗ (7) \frac{(a+b)/2-x}{x^{*}-(a+b)/2 }=\frac{h}{h^{*}} \tag7 x∗−(a+b)/2(a+b)/2−x=h∗h(7)
对公式(7)进行转换,即可得到反向解x*的表达式为:
x ∗ = a + b 2 + a + b 2 k − x k (8) x^{*} =\frac{a+b}{2}+\frac{a+b}{2k}-\frac{x}{k} \tag8 x∗=2a+b+2ka+b−kx(8)
其中, k = h / h ∗ k=h/h^{*} k=h/h∗, a a a和 b b b可以视为某维度的上下限。本文中的 k k k是一个与迭代次数相关的动态自适应值。
3. 部分代码展示
close all
clear
clcSearchAgents_no=30; % Number of search agentsFunction_name='F4'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)Max_iteration=500; % Maximum numbef of iterations% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);[OMA_Best_score,OMA_Best_pos,OMA_cg_curve]=OMA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[IOMA_Best_score,IOMA_Best_pos,IOMA_cg_curve]=IOMA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);figure('Position',[500 500 660 290])
% Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])% Draw objective space
subplot(1,2,2);
semilogy(OMA_cg_curve,'Color','k','Linewidth',1.5)
hold on
semilogy(IOMA_cg_curve,'Color','r','Linewidth',1.5)
title('寻优过程')
xlabel('迭代次数');
ylabel('适应度值曲线');axis tight
grid on
box on
legend('OMA','IOMA')display(['The best solution obtained by OMA is : ', num2str(OMA_Best_pos)]);
display(['The best optimal value of the objective funciton found by OMA is : ', num2str(OMA_Best_score)]);
display(['The best solution obtained by IOMA is : ', num2str(IOMA_Best_pos)]);
display(['The best optimal value of the objective funciton found by IOMA is : ', num2str(IOMA_Best_score)]);
4. 仿真结果展示





5. 资源获取说明
可以获取完整代码资源。
相关文章:

【群智能算法改进】一种改进的光学显微镜算法 IOMA算法[1]【Matlab代码#60】
文章目录 【获取资源请见文章第5节:资源获取】1. 光学显微镜算法(OMA)1.1 物镜放大倍数1.2 目镜放大倍数 2. 改进后的IOMA算法2.1 透镜成像折射方向学习 3. 部分代码展示4. 仿真结果展示5. 资源获取说明 【获取资源请见文章第5节:…...
第三课-软件升级-Stable Diffusion教程
前言: 虽然第二课已经安装好了 SD,但你可能在其它地方课程中,会发现很多人用的和你的界面差距很大。这篇文章会讲一些容易忽略或者常常需要做的操作,不一定要完全照做,以后再回过头看看也可以。 1.控制类型 问题:为什么别人有“控制类型”部分,而我没有?如下红色方框…...

【C++】设计模式之——建造者
建造者模式概念模拟实现建造者模式代码实现 建造者模式 首先先大体了解一下,建造者模式是什么意思,它是怎么实现的? 首先,建造者模式是一种创建型设计模式再一个它是使用多个简单的对象一步一步的搭建出一个复杂的对象它可以将一个…...
)
【C++】基础语句(学习笔记)
一、分支 1、三种基本结构 顺序结构分支结构循环结构 2、if与switch对比 1)使用场景 switch只支持常量值固定相等的分支判断if可以判断区间范围用switch能做的,用if都能做 2)性能比较 分支少时,差别不是很大。分支多时&…...

大厂秋招真题【DP】米哈游20230924秋招T2-米小游与魔法少女-奇运
米哈游20230924秋招T2-米小游与魔法少女-奇运 题目描述与示例 题目描述 米小游都快保底了还没抽到希儿,好生气哦!只能打会活动再拿点水晶。 米小游和世界第一可爱的魔法少女 TeRiRi 正在打 BOSS,BOSS 的血量为h,当 BOSS 血量小…...
LVS+Keepalived 高可用集群负载均衡
一.keepalived介绍 1.1.Keepalived实现原理 由多台路由器组成一个热备组,通过共用的虚拟IP地址对外提供服务。 每个热备组内同时只有一台主路由器提供服务,其他路由器处于冗余状态。 若当前在线的路由器失效,则其他路由器会根据设置…...

Qt QList类和QLinkedList类 详解
一、QList 类 对于不同的数据类型,QList<T>采取不同的存储策略,存储策略如下: 如果T 是一个指针类型或指针大小的基本类型(该基本类型占有的字节数和指针类型占有的字节数相同),QList<T>将数值直接存储在它的数组当…...

Mac安装GYM遇到的一些坑
以下是遇到的一些问题 安装GitHub上说的直接 pip install gym成功了,但是运行实例报错没安装gym[classic_control],所以就全安装一下[all] 安装GitHub上说的直接 pip install gym成功了,但是运行实例报错没安装gym[classic_control]ÿ…...
【高级rabbitmq】
文章目录 1. 消息丢失问题1.1 发送者消息丢失1.2 MQ消息丢失1.3 消费者消息丢失1.3.1 消费失败重试机制 总结 2. 死信交换机2.1 TTL 3. 惰性队列3.1 总结: 4. MQ集群 消息队列在使用过程中,面临着很多实际问题需要思考: 1. 消息丢失问题 1.1…...
数百个下载能够传播 Rootkit 的恶意 NPM 软件包
供应链安全公司 ReversingLabs 警告称,最近观察到的一次恶意活动依靠拼写错误来诱骗用户下载恶意 NPM 软件包,该软件包会通过 rootkit 感染他们的系统。 该恶意软件包名为“node-hide-console-windows”,旨在模仿 NPM 存储库上合法的“node-…...

SpringBoot的error用全局异常去处理
记录一下使用SpringBoot2.0.5的error用全局异常去处理 在使用springboot时,当访问的http地址或者说是请求地址输错后,会返回一个页面,如下: 这是因为请求的地址不存在,默认会显示error页面 但我们实际需要一个接口&a…...
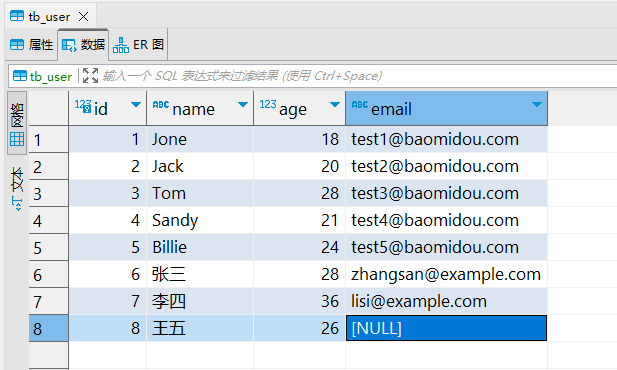
MyBatisPlus(十一)包含查询:in
说明 包含查询,对应SQL语句中的 in 语句,查询参数包含在入参列表之内的数据。 in Testvoid inNonEmptyList() {// 非空列表,作为参数List<Integer> ages Stream.of(18, 20, 22).collect(Collectors.toList());in(ages);}Testvoid in…...

Linux命令定位与查找:which、whereis和find的用法详解
文章目录 Linux命令的定位与查找1. 简介Linux路径环境变量命令行和Shell 2. which命令which命令的作用使用which命令定位可执行文件多个可执行文件的定位which命令的选项及其使用 3. whereis命令whereis命令的作用使用whereis命令查找二进制文件查找源代码文件whereis命令的选项…...

LeetCode 面试题 17.10. Find Majority Element LCCI【摩尔投票法】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

多校联测11 模板题
题目大意 给你四个整数 n , m , s e e d , w n,m,seed,w n,m,seed,w,其中 n , m n,m n,m为两个多项式 A ( x ) ∑ i 0 n a i x i A(x)\sum\limits_{i0}^na_ix^i A(x)i0∑naixi和 B ( x ) ∑ i 0 m b i x i B(x)\sum\limits_{i0}^mb_ix^i B(x)i0∑mbixi…...
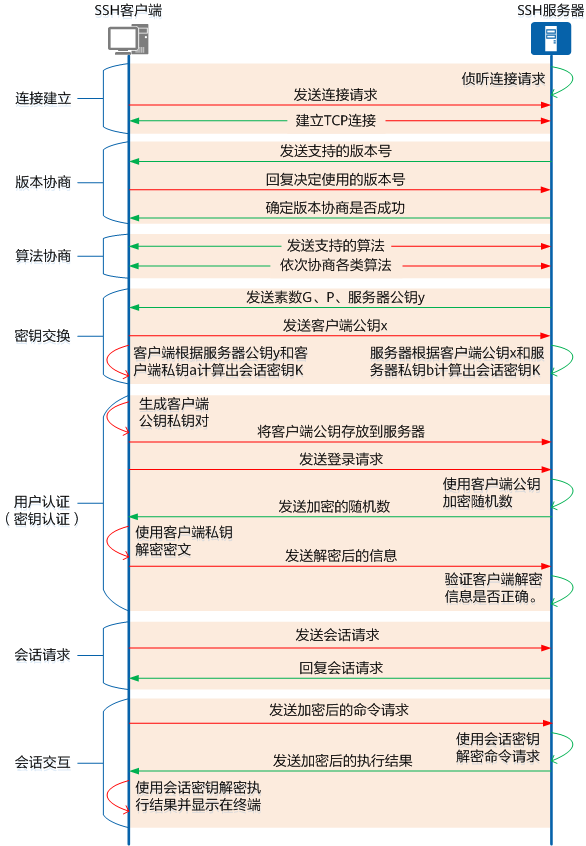
Linux SSH连接远程服务器(免密登录、scp和sftp传输文件)
1 SSH简介 SSH(Secure Shell,安全外壳)是一种网络安全协议,通过加密和认证机制实现安全的访问和文件传输等业务。传统远程登录和文件传输方式,例如Telnet、FTP,使用明文传输数据,存在很多的安全…...
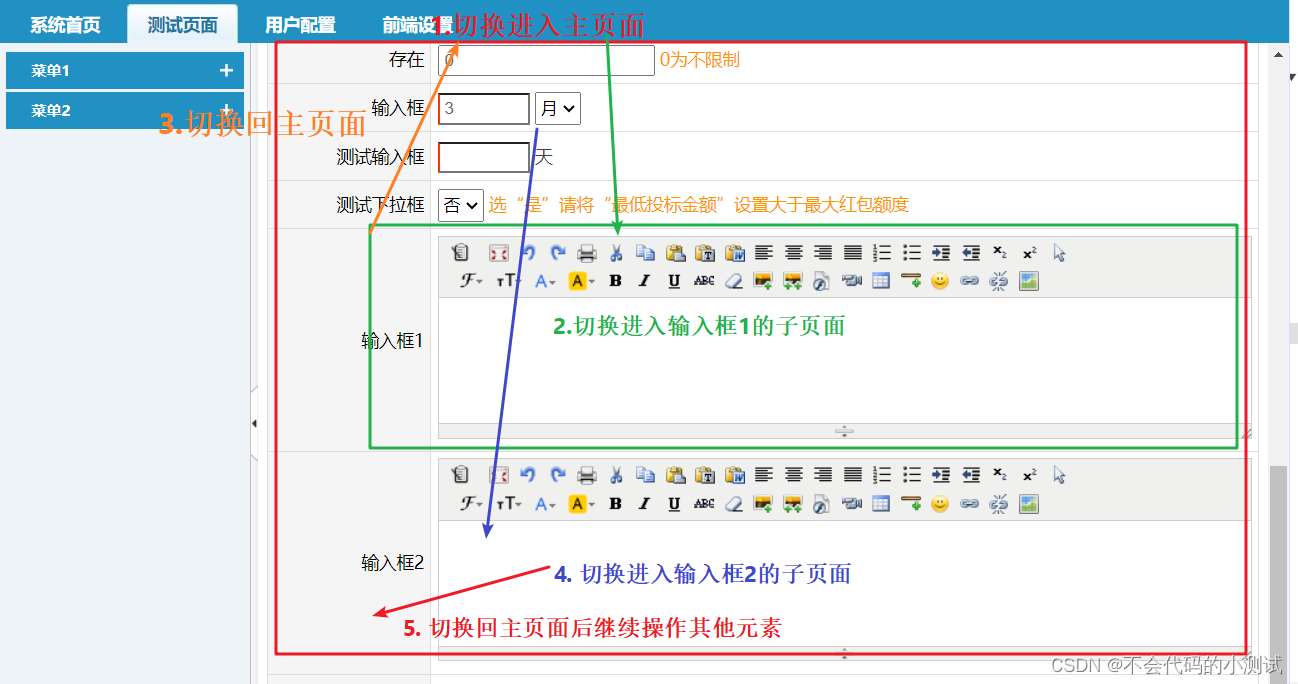
从0开始python学习-30.selenium frame子页面切换
目录 1. frame切换逻辑 2. 多层子页面情况进行切换 3. 多个子页面相互切换 1. frame切换逻辑 1.1. 子页面的类型一般分为两种 frame标签 iframe标签 1.2. 子页面里面的元素和主页面的元素是相互独立 子页面元素需要进去切换才能操作 如果已经进入子页面,那么…...
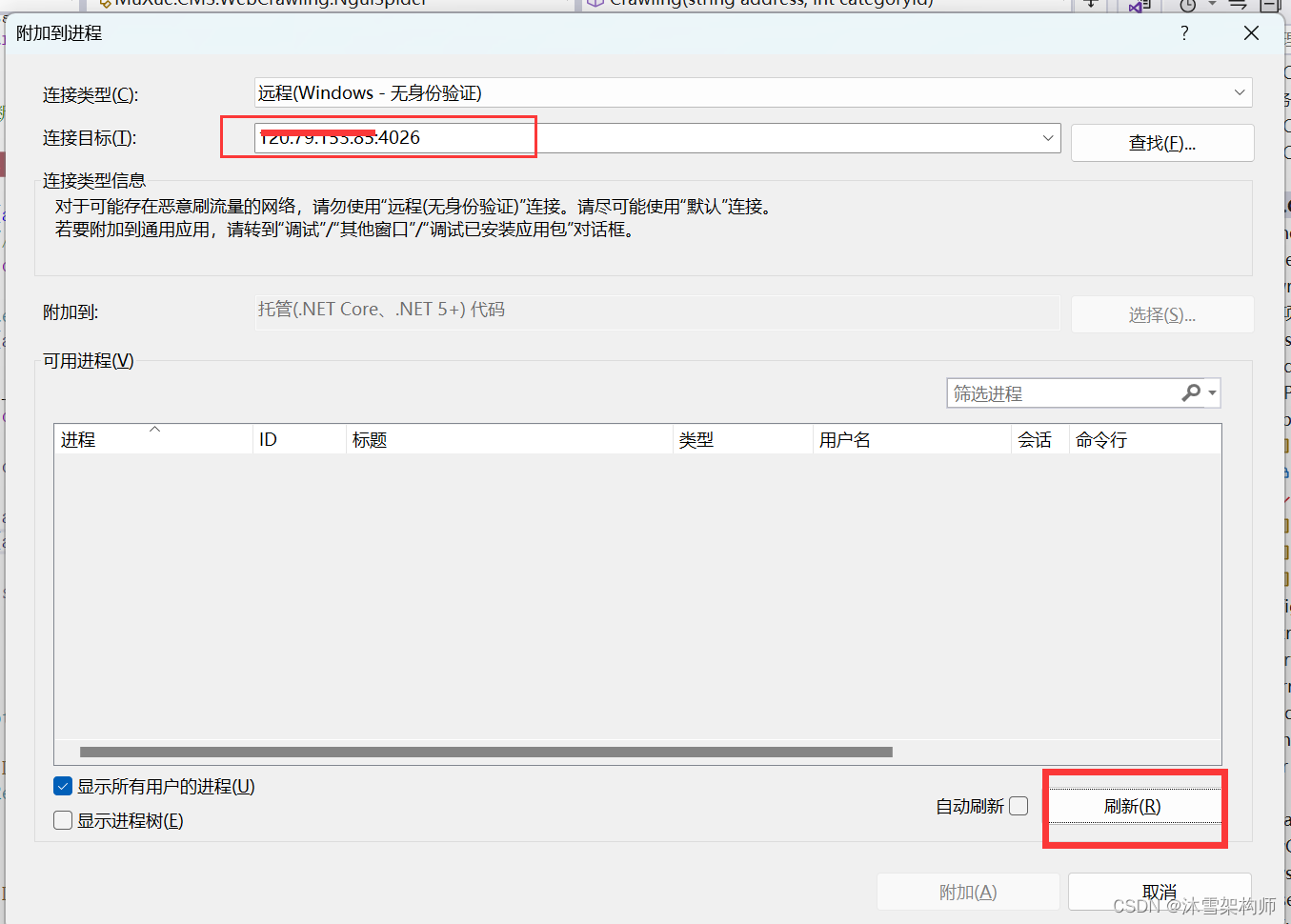
asp.net core 远程调试
大概说下过程: 1、站点发布使用Debug模式 2、拷贝到远程服务器,以及iis创建站点。 3、本地的VS2022的安装目录:C:\Program Files\Microsoft Visual Studio\2022\Professional\Common7\IDE下找Remote Debugger 你的服务器是64位就拷贝x64的目…...

Java spring boot 一次调用多个请求
Java Spring Boot是一种基于Java编程语言的开发框架,它提供了一种快速构建高效、可伸缩和易于维护的企业级应用程序的方式。在实际的应用开发中,我们常常需要调用多个独立的请求来完成某个业务功能。然而,传统的同步方式一次只能调用一个请求…...
)
DRM全解析 —— CRTC详解(4)
接前一篇文章:DRM全解析 —— CRTC详解(3) 本文继续对DRM中CRTC的核心结构struct drm_crtc的成员进行释义。 3. drm_crtc结构释义 (21)struct drm_object_properties properties /** properties: property tracking …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
