多校联测11 8ady
题目大意
有一个排列 a 1 , a 2 , … , a n a_1,a_2,\dots,a_n a1,a2,…,an,我们现在进行如下操作:
for(int i=1;i<=n-m+1;i++) sort(a+i,a+i+m);
设最后的结果为 b 1 , b 2 , ⋯ , b n b_1,b_2,\cdots,b_n b1,b2,⋯,bn,求满足条件的 a a a中字典序第 k k k小的 a a a。
1 ≤ n ≤ 1 0 6 , m ≤ n , 1 ≤ k ≤ 1 0 18 1\leq n\leq 10^6,m\leq n,1\leq k\leq 10^{18} 1≤n≤106,m≤n,1≤k≤1018, b i b_i bi是 1 1 1到 n n n的一个排列。
题解
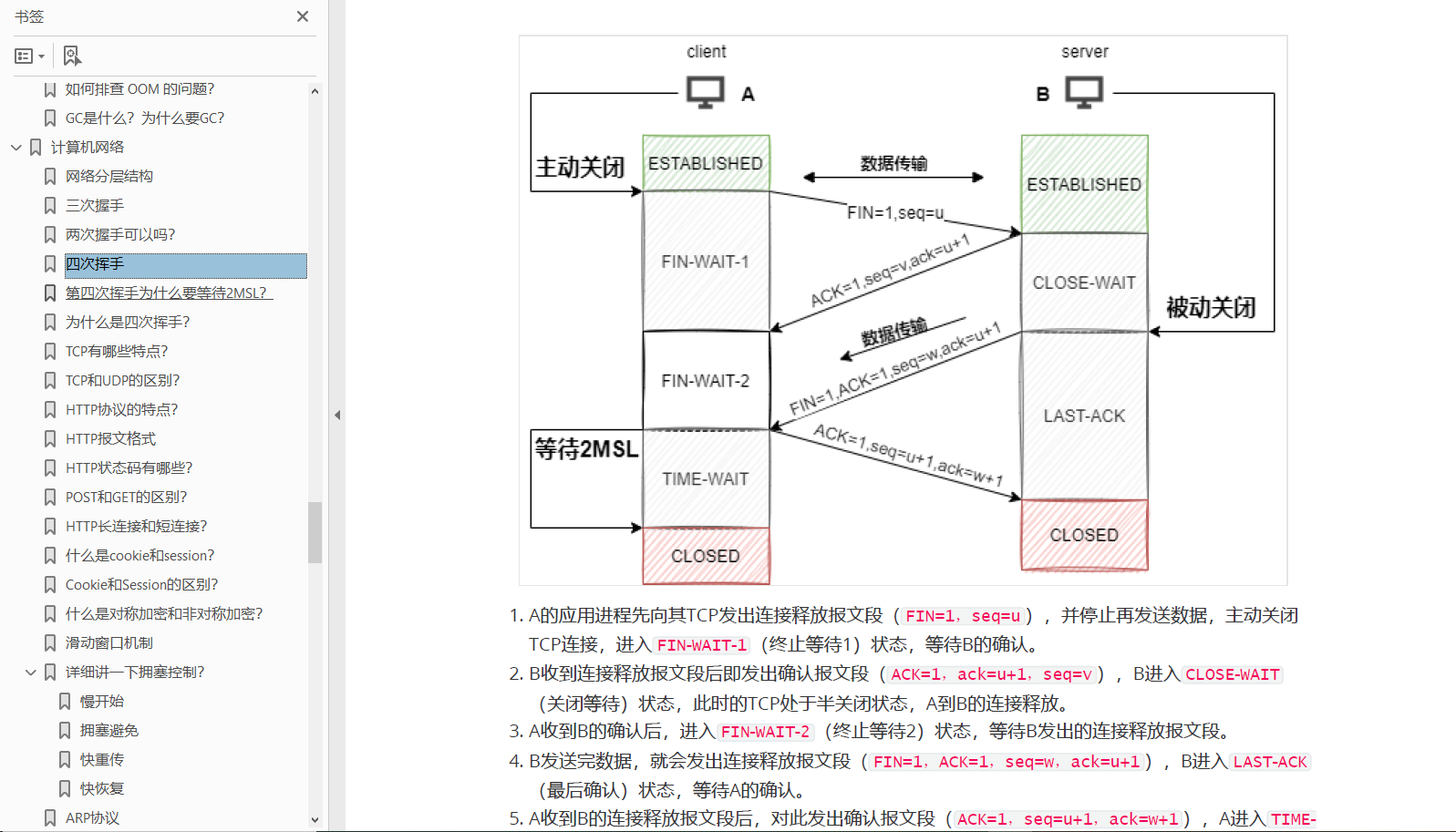
由题意可得 b i b_i bi是 a 1 , a 2 , … , a min ( i + m − 1 , n ) a_1,a_2,\dots,a_{\min(i+m-1,n)} a1,a2,…,amin(i+m−1,n)中,满足不在 b 1 , b 2 , … , b i − 1 b_1,b_2,\dots,b_{i-1} b1,b2,…,bi−1中的最小的数。
那么,当 b i − 1 > b i b_{i-1}>b_i bi−1>bi,就一定有 a i + m − 1 = b i a_{i+m-1}=b_i ai+m−1=bi。
把这些已经确定的 b i b_i bi去掉,剩下的问题等价于 n n n变小, m , k m,k m,k不变, b i = i b_i=i bi=i的子问题。
下面,我们假设 b i = i b_i=i bi=i。
考虑从小到大将每一个 i i i填入 a a a中,易得 i i i需要填在 [ 1 , min ( i + m − 1 , n ) ] [1,\min(i+m-1,n)] [1,min(i+m−1,n)]中任意没填过的位置,那么填 i i i的方案数为 min ( m , n − i + 1 ) \min(m,n-i+1) min(m,n−i+1)。
然而,因为方案数很大,而 k k k相对没那么大,所以 a a a有一个前缀都满足 a i = i a_i=i ai=i。
设 f i f_i fi表示满足上面条件的前缀为 n − i n-i n−i,也就是后面有最多 i i i个数不满足,那么
f i = f i − 1 × min ( m , i ) f_i=f_{i-1}\times \min(m,i) fi=fi−1×min(m,i)
当 m = 1 m=1 m=1时,显然只有一个答案。因为保证有解,这种情况下 k = 1 k=1 k=1。
当 m > 1 m>1 m>1时, f i ≥ 2 i − 1 f_i\geq 2^{i-1} fi≥2i−1,可得 f 62 ≥ k f_{62}\geq k f62≥k
那么,我们只需取最后 min ( n , 62 ) \min(n,62) min(n,62)个位置,后面用一个状压维护状态,再枚举每一位填什么即可。细节见代码。
时间复杂度为 O ( n + v 3 ) O(n+v^3) O(n+v3),其中 v = min ( n , 62 ) v=\min(n,62) v=min(n,62)。
code
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000005],b[1000005],c[1000005],num[1000005],z[1000005];
long long k;
long long gt(int t,int w,long long now){long long re=1;for(int i=1;i<=t;i++){if((now>>i-1)&1){if(re>k/(min(i+m-1,t)-w)+1) return k+1;re=re*(min(i+m-1,t)-w);if(re>k) return k+1;++w;}}return re;
}
void dd(int l,int t){long long now=(1ll<<t)-1;for(int i=1;i<=l-t;i++) c[i]=num[i];for(int i=t;i>=1;i--){for(int j=1;j<=t;j++){if((now>>j-1)&1){long long vt=gt(t,t-i+1,now^(1ll<<j-1));if(k>=vt) k-=vt;else{c[l-i+1]=num[l-t+j];now^=(1ll<<j-1);break;}}}}
}
int main()
{scanf("%d%d%lld",&n,&m,&k);--k;for(int i=1;i<=n;i++){scanf("%d",&b[i]);}int lst=b[1],cnt=0;for(int i=2;i<=n;i++){if(lst>b[i]){a[i+m-1]=b[i];z[b[i]]=1;}else lst=b[i];}for(int i=1;i<=n;i++){if(!z[i]) num[++cnt]=i;}dd(cnt,min(cnt,62));int now=1;for(int i=1;i<=n;i++){if(!a[i]){a[i]=c[now];++now;}printf("%d ",a[i]);}return 0;
}
相关文章:

多校联测11 8ady
题目大意 有一个排列 a 1 , a 2 , … , a n a_1,a_2,\dots,a_n a1,a2,…,an,我们现在进行如下操作: for(int i1;i<n-m1;i) sort(ai,aim);设最后的结果为 b 1 , b 2 , ⋯ , b n b_1,b_2,\cdots,b_n b1,b2,⋯,bn,求满足条件的…...
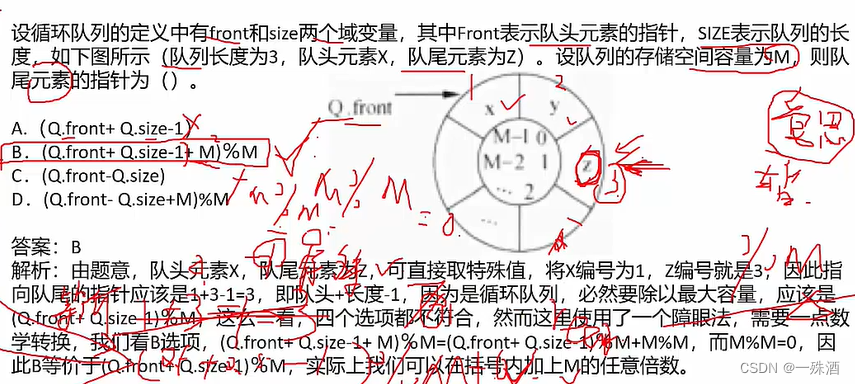
【软考】9.1 顺序表/链表/栈和队列
《线性结构》 顺序存储和链表存储 每个元素最多只有一个出度和一个入度,表现为一条线状链表存储结构:每个节点有两个域,即数据,指针域(指向下一个逻辑上相邻的节点) 时间复杂度:与其数量级成正…...

来 来 来 国家开放大学模拟题型 训练
试卷代号:2110 行政法与行政诉讼法 参考试题 一、单项选择题(每小题只有一项正确答案,请将正确答案的序号填在括号内。每小题2分,共20分) 1.下列案件中属于行政诉讼受案范围的是( )。 A.因人民政府对某工作人员的…...
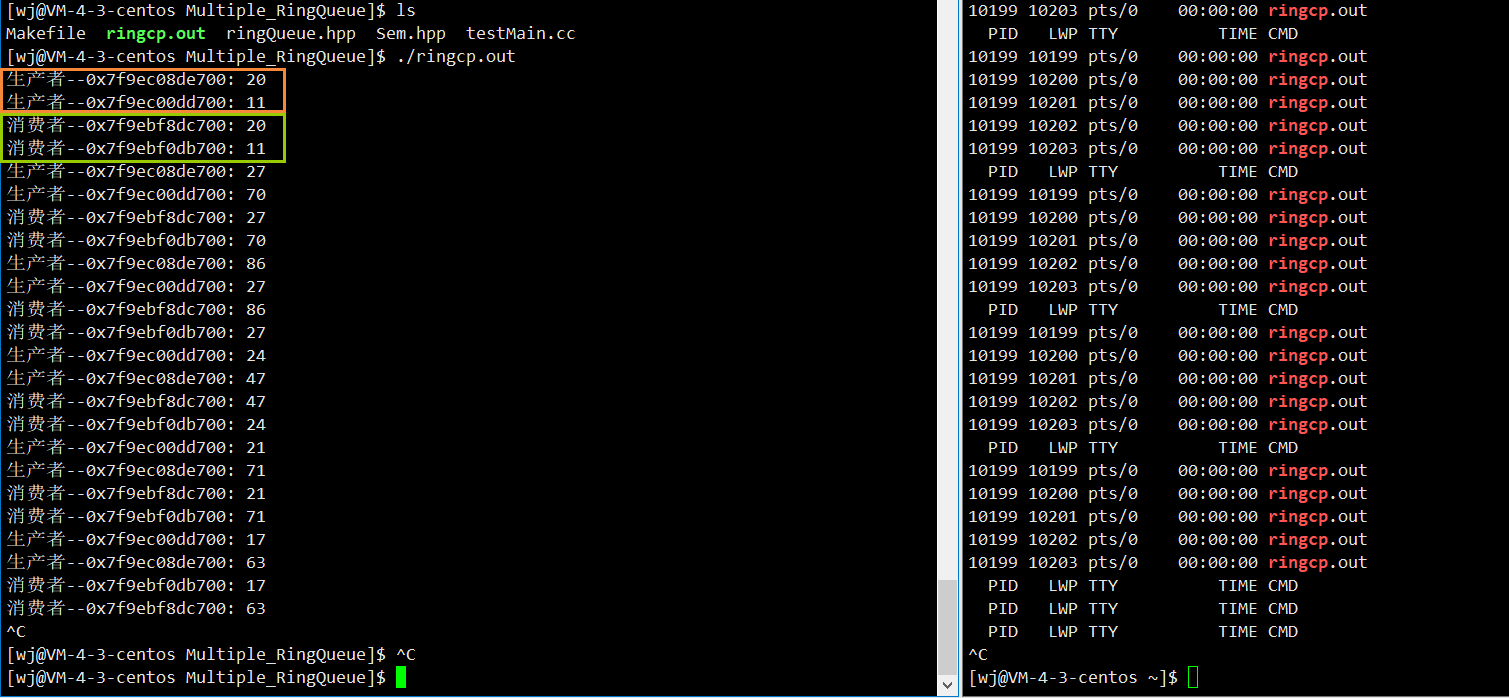
【ONE·Linux || 多线程(二)】
总言 多线程:生产者消费者模型与两种实现方式(条件变量、信号量)、线程池。 文章目录 总言4、生产者消费者模型4.1、基本概念4.2、基于BlockingQueue的生产者消费者模型(理解条件变量)4.2.1、单生产者单消费者模式&am…...

pandas.DataFrame.to_excel:在同一个sheet内追加数据
参考了这篇文章的方法 pandas to_excel:写入数据,在同一个sheet中追加数据,写入到多个sheet里,基本逻辑是: 通过数据框获取到该Excel表的行数 df_rows,然后将需要存储的数据,限制开始写入的行数,…...

基于卷积神经网络的图像识别技术研究与实践
基于卷积神经网络的图像识别技术研究与实践 卷积神经网络(CNN)是一种深度学习模型,它在图像识别领域取得了显著的成果。本文旨在探讨基于卷积神经网络的图像识别技术研究与实践。 一、卷积神经网络概述 卷积神经网络是一种深度学习模型&am…...

Linux防火墙之--SNAT和DNAT
1.SNAT是什么 SNAT又称源地址转换。源地址转换是内网地址向外访问时,发起访问的内网ip地址转换为指定的ip地址(可指定具体的服务以及相应的端口或端口范围),这可以使内网中使用保留ip地址的主机访问外部网络,即内网的多…...

Bean注入方式:@Autowired、@Resource的区别
Autowired 和 Resource 的区别是什么? Autowired 属于 Spring 内置的注解,默认的注入方式为 byType(根据类型进行匹配),也就是说会优先根据接口类型去匹配并注入 Bean (接口的实现类)。 这会有…...

软件设计原则 1小时系列 (C++版)
文章目录 前言基本概念 Design Principles⭐单一职责原则(SRP) Single Responsibility PrincipleCode ⭐里氏替换原则(LSP) Liskov Substitution PrincipleCode ⭐开闭原则(OCP) Open Closed PrincipleCode ⭐依赖倒置原则(DIP) Dependency Inversion PrincipleCode ⭐接口隔离…...
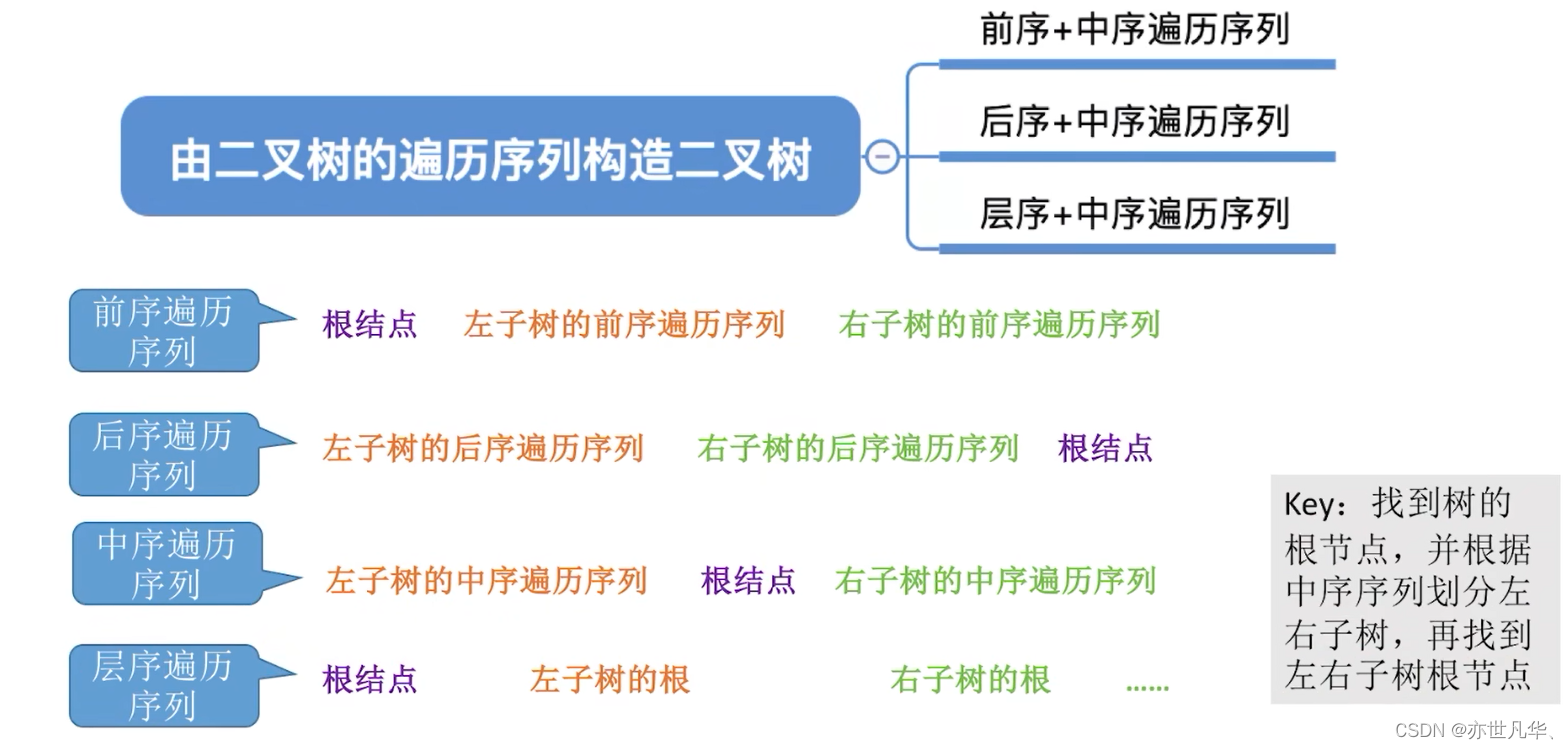
数据结构--》解锁数据结构中树与二叉树的奥秘(一)
数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。 无论你是初学者还是进阶者&…...
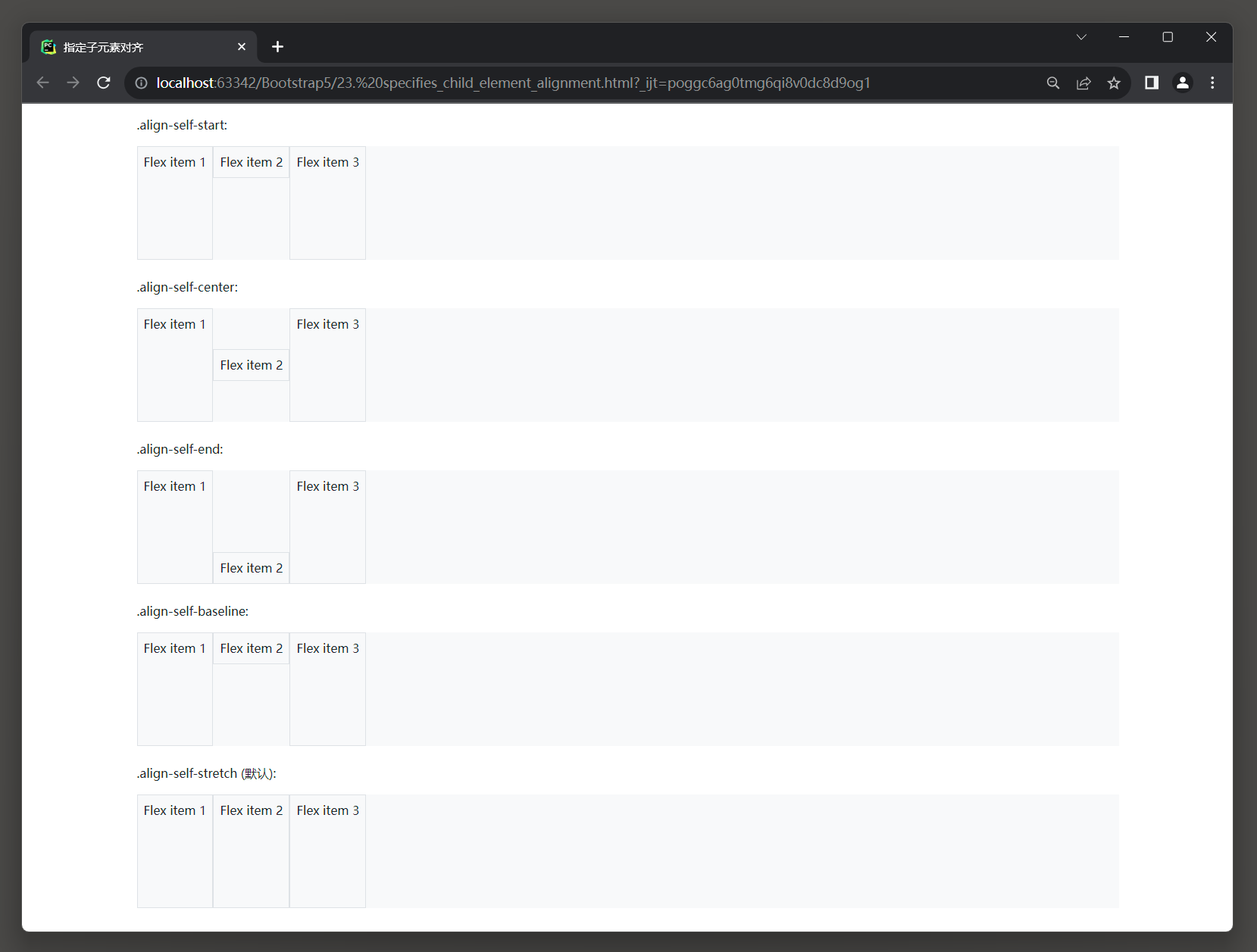
23.4 Bootstrap 框架5
1. 背景颜色 1.1 背景颜色样式 在Bootstrap 5中, 可以使用以下类来设置背景颜色: * 1. .bg-primary: 设置为主要的背景颜色(#007bff, 深蓝色). * 2. .bg-secondary: 设置为次要的背景颜色(#6c757d, 灰色). * 3. .bg-success: 设置为成功的背景颜色(#28a745, 绿色). * 4. …...
Spring源码解析——IOC属性填充
正文 doCreateBean() 主要用于完成 bean 的创建和初始化工作,我们可以将其分为四个过程: 最全面的Java面试网站 createBeanInstance() 实例化 beanpopulateBean() 属性填充循环依赖的处理initializeBean() 初始化 bean 第一个过程实例化 bean在前面一篇…...

寒露到了,冬天还会远吗?
寒露惊秋晚,朝看菊渐黄。 日复一日间,光影如梭,我们便很快将告别了秋高气爽,白日将变得幽晦, 天寒夜长,风气萧索,雾结烟愁。 还没好好体会秋高气爽,寒露就到了。 今天晚上9点多,我们…...

科普②| 大数据有什么用?大数据技术的应用领域有哪些?
1、提供个性服务很多人觉得大数据好像离我们很远,其实我们在日常所使用的智能设备,就需要大数据的帮助。比如说我们运动时候戴的运动手表或者是运动手环,就可以在我们平时运动的时候,帮助我们采集运动数据及热量消耗情况。进入睡眠…...

golang的切片使用总结二
如果没看golang切片的第一篇总结博客 golang的切片使用总结一-CSDN博客 ,请浏览之 举例9:make([]int, a, b)后访问下标a的元素 s : make([]int, 10, 12) v : s[10] fmt.Printf("v:%v", v) 打印结果: panic: runtime error: index …...
tailscale自建headscale和derp中继
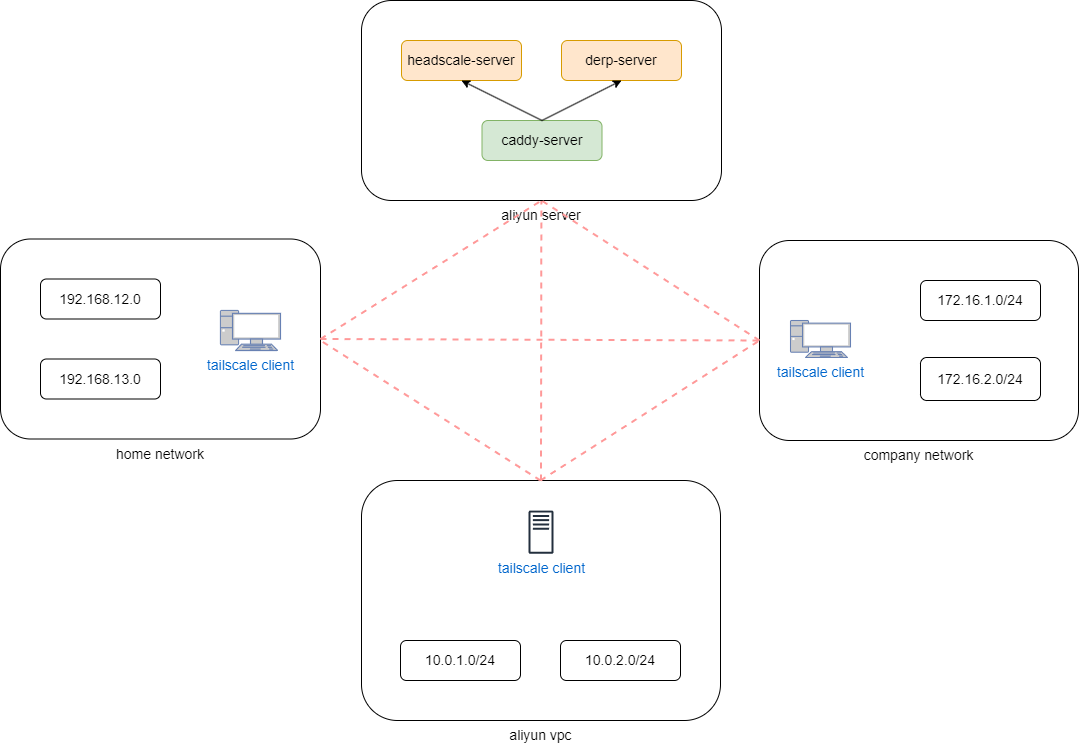
tailscale derp中继服务简介 tailscale是一个基于WireGuard的零配置软件,它可以轻松地在多台设备之间建立点对点加密连接。 derp服务器是tailscale网络的重要组成部分。它作为tailscale客户端之间的中继,帮助客户端找到并连接到其他客户端设备。 但Tailscale 官方…...
布隆过滤器的使用
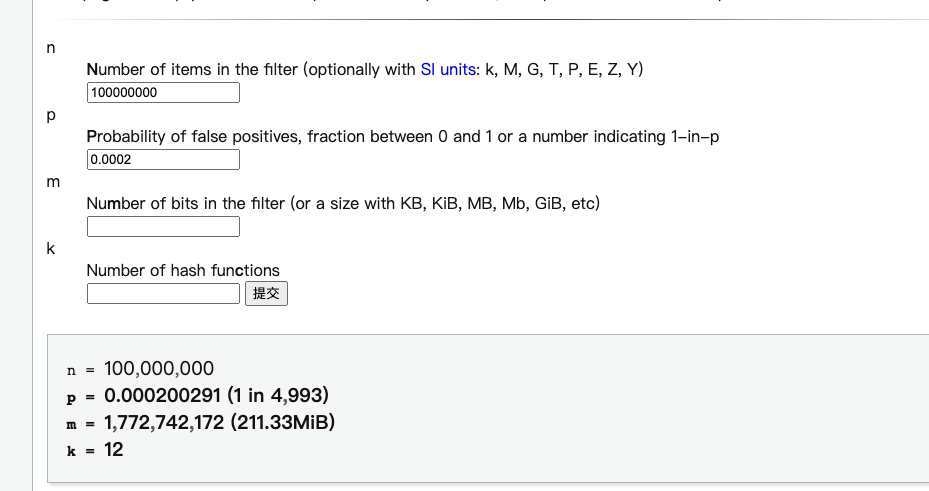
布隆过滤器简介 Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。 布隆过滤器的优势在于,利用很少的空…...

Web开发-单例模式
目录 单例模式介绍代码实现单例模式 单例模式介绍 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。单例模式通…...
MySQL:温备份和恢复-mysqldump (4)
介绍 温备:同样是在数据库运行的时候进行备份的,但对当前数据库的操作会产生影响。(只可以读操作,不可以写操作) 温备份的优点: 1.可在表空间或数据文件级备份,备份时间短。 2.备份时数据库依然…...
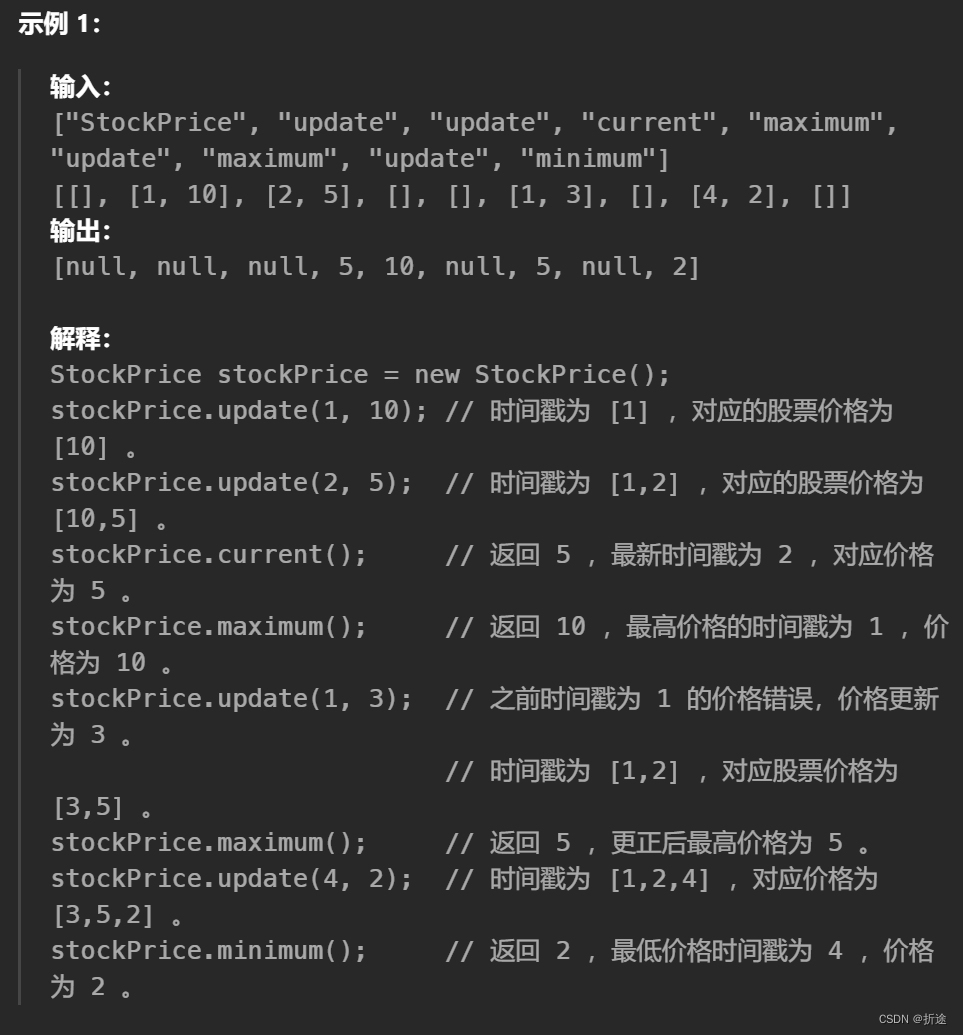
【力扣每日一题】2023.10.8 股票价格波动
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题是程序设计题,要我们实现一个类,一共是四个功能,第一个是给一个时间戳和价格,表示该…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
