贪心找性质+dp表示+矩阵表示+线段树维护:CF573D
比较套路的题目
首先肯定贪心一波,两个都排序后尽量相连。我一开始猜最多跨1,但其实最多跨2,考虑3个人的情况:

我们发现第3个人没了,所以可以出现跨2的情况
然后直接上dp,由 i − 1 , i − 2 , i − 3 i-1,i-2,i-3 i−1,i−2,i−3 转移过来。
然后这显然可以拿矩阵表示。
然后显然可以拿线段树维护。
后面三部分都是比较套路的。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//#define M
//#define mo
#define N 30010
int n, m, i, j, k, T;
int a[N], b[N], ia[N], ib[N], shu[N], pos[N], x, y, q, rt; int Not(int x, int y) { if(shu[ia[x]]!=ib[y]) return 1; return 0; }struct Martix {int c[3][3]; void mem() { memset(c, 0, sizeof(c)); }void init() { mem(); c[0][0]=c[1][1]=c[2][2]=1; }void min() { c[0][0]=c[0][1]=c[0][2]=c[1][0]=c[1][1]=c[1][2]=c[2][1]=c[2][2]=c[2][0]=-1e15; }Martix operator *(const Martix A) const { //max+Martix B; B.min(); for(int i=0; i<3; ++i) for(int j=0; j<3; ++j) for(int k=0; k<3; ++k) B.c[i][j]=max(B.c[i][j], c[i][k]+A.c[k][j]); return B; }void make(int x) {//生成在x位置的矩阵 min(); c[1][0]=c[2][1]=0; if(Not(x, x)) c[0][0]=a[x]*b[x];
// if(x==1) return printf("# 1 : \n"), (*this).print(), void(); if(x==1) return ; if(Not(x, x-1) && Not(x-1, x)) c[0][1]=a[x]*b[x-1]+a[x-1]*b[x];
// if(x==2) return printf("# 2: \n"), (*this).print(), void(); if(x==2) return ; if(Not(x, x-1) && Not(x-1, x-2) && Not(x-2, x)) c[0][2]=max(c[0][2], a[x]*b[x-1]+a[x-1]*b[x-2]+a[x-2]*b[x]); if(Not(x, x-2) && Not(x-1, x) && Not(x-2, x-1)) c[0][2]=max(c[0][2], a[x]*b[x-2]+a[x-1]*b[x]+a[x-2]*b[x-1]); if(Not(x, x-2) && Not(x-1, x-1) && Not(x-2, x)) c[0][2]=max(c[0][2], a[x]*b[x-2]+a[x-1]*b[x-1]+a[x-2]*b[x]);
// printf("# %lld : \n", x); (*this).print(); }int que() {
// printf("RT : ");
// (*this).print(); Martix B; B.min(); B.c[0][0]=0; B=(*this)*B; return B.c[0][0]; }void print() {
printf("---\n"); for(int i=0; i<3; ++i, printf("\n")) for(int j=0; j<3; ++j) printf("%lld ", c[i][j]); printf("\n"); }
};struct Segment_tree {int tot, ls[N<<2], rs[N<<2]; Martix s[N<<2]; void push_up(int k) { s[k]=s[rs[k]]*s[ls[k]]; } //注意乘法顺序 void build(int &k, int l, int r) {if(!k) k=++tot; if(l==r) return s[k].make(l), void(); int mid=(l+r)>>1; build(ls[k], l, mid); build(rs[k], mid+1, r); push_up(k); }void modify(int k, int l, int r, int x) {if(l==r) return s[k].make(x), void(); int mid=(l+r)>>1; if(x<=mid) modify(ls[k], l, mid, x); else modify(rs[k], mid+1, r, x); push_up(k);
// printf("[%lld %lld] : \n", l, r); s[k].print(); }
}Seg;signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// srand(time(NULL));
// T=read();
// while(T--) {
//
// }n=read(); q=read(); for(i=1; i<=n; ++i) a[i]=read(), ia[i]=i, shu[i]=i; //shu:第i个人马的编号 for(i=1; i<=n; ++i) b[i]=read(), ib[i]=i; sort(ia+1, ia+n+1, [] (int x, int y) { return a[x]>a[y]; }); sort(ib+1, ib+n+1, [] (int x, int y) { return b[x]>b[y]; }); sort(a+1, a+n+1); reverse(a+1, a+n+1); //按实力排好,则原顺序已经没必要了 sort(b+1, b+n+1); reverse(b+1, b+n+1);
// cout<<"ia : "; for(i=1; i<=n; ++i) printf("%lld ", ia[i]); puts("");
// cout<<"ib : "; for(i=1; i<=n; ++i) printf("%lld ", ib[i]); puts("");
// cout<<"a : "; for(i=1; i<=n; ++i) printf("%lld ", a[i]); puts("");
// cout<<"b : "; for(i=1; i<=n; ++i) printf("%lld ", b[i]); puts(""); //ia, ib排序后排名第i对应的原编号 for(i=1; i<=n; ++i) pos[ia[i]]=i; //某编号对应的排名
// cout<<"pos : "; for(i=1; i<=n; ++i) printf("%lld ", pos[i]); puts(""); Seg.build(rt, 1, n); while(q--) {x=read(); y=read(); swap(shu[x], shu[y]); //交换了马
// cout<<"shu : "; for(i=1; i<=n; ++i) printf("%lld ", shu[i]); puts(""); for(i=max(1ll, pos[x]-3); i<=min(n, pos[x]+3); ++i) Seg.modify(1, 1, n, i); for(i=max(1ll, pos[y]-3); i<=min(n, pos[y]+3); ++i) Seg.modify(1, 1, n, i); printf("%lld\n", Seg.s[1].que()); }return 0;
}相关文章:

贪心找性质+dp表示+矩阵表示+线段树维护:CF573D
比较套路的题目 首先肯定贪心一波,两个都排序后尽量相连。我一开始猜最多跨1,但其实最多跨2,考虑3个人的情况: 我们发现第3个人没了,所以可以出现跨2的情况 然后直接上dp,由 i − 1 , i − 2 , i − 3 i…...
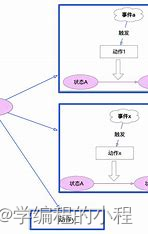
小谈设计模式(17)—状态模式
小谈设计模式(17)—状态模式 专栏介绍专栏地址专栏介绍 状态模式关键角色上下文(Context)抽象状态(State)具体状态(Concrete State) 核心思想Java程序实现首先,我们定义一个抽象状态类 State,其中包含一个处理请求的方法 handleRe…...

Arm64体系架构-MPIDR_EL1寄存器
背景 在Arm64多核处理器中, 各核间的关系可能不同. 比如1个16 core的cpu, 每4个core划分为1个cluster,共享L2 cache. 当我们需要从core 0将任务调度出来时,如果优先选择core 1~3, 那么性能明显时优于其他core的. 那么操作系统怎么知道core之间这样的拓扑信息呢? Arm提供了MPID…...

MySQL支持哪些存储引擎
mysql支持九大存储引擎: 1)MYISAM存储引擎(优点:可被转换为压缩、只读表来节省空间。) 它管理的表具有以下特征: 使用三个文件表示每个表 格式文件-存储表结构的定义(mytable.frm) 数据文件-存…...

ElementUI结合Vue完成主页的CUD(增删改)表单验证
目录 一、CUD ( 1 ) CU讲述 ( 2 ) 编写 1. CU 2. 删除 二、验证 前端整合代码 : 一、CUD 以下的代码基于我博客中的代码进行续写 : 使用ElementUI结合Vue导航菜单和后台数据分页查询 ( 1 ) CU讲述 在CRUD操作中,CU代表创建(Create)…...
Flutter开发笔记 —— 语音消息功能实现
前言 最近在开发一款即时通讯(IM)的聊天App,在实现语音消息功能模块后,写下该文章以做记录。 注:本文不提供相关图片资源以及IM聊天中具体实现代码,单论语音功能实现思路 需求分析 比起上来直接贴代码,我们先来逐步…...
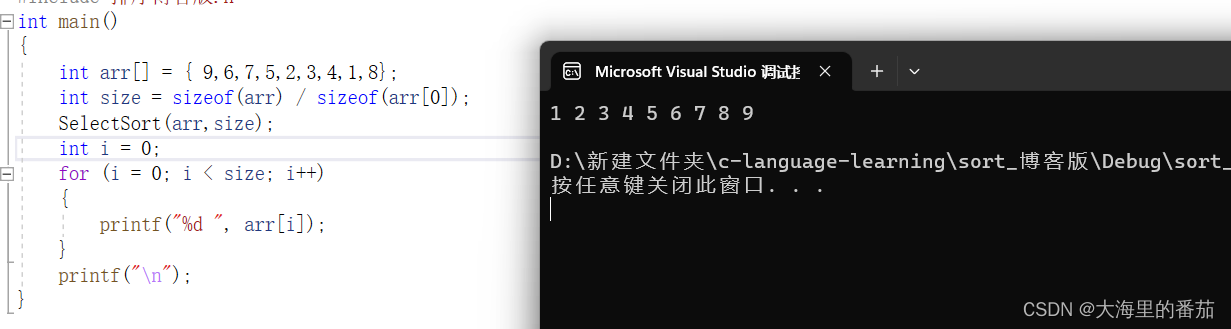
冒泡排序和选择排序
目录 一、冒泡排序 1.冒泡排序的原理 2.实现冒泡排序 1.交换函数 2.单躺排序 3.冒泡排序实现 4.测试 5.升级冒泡排序 6.升级版代码 7.升级版测试 二、选择排序 1.选择排序的原理 2.实现选择排序 1.单躺排序 2.选择排序实现 3.测试 4.修改 5.测试 一、冒泡排序…...
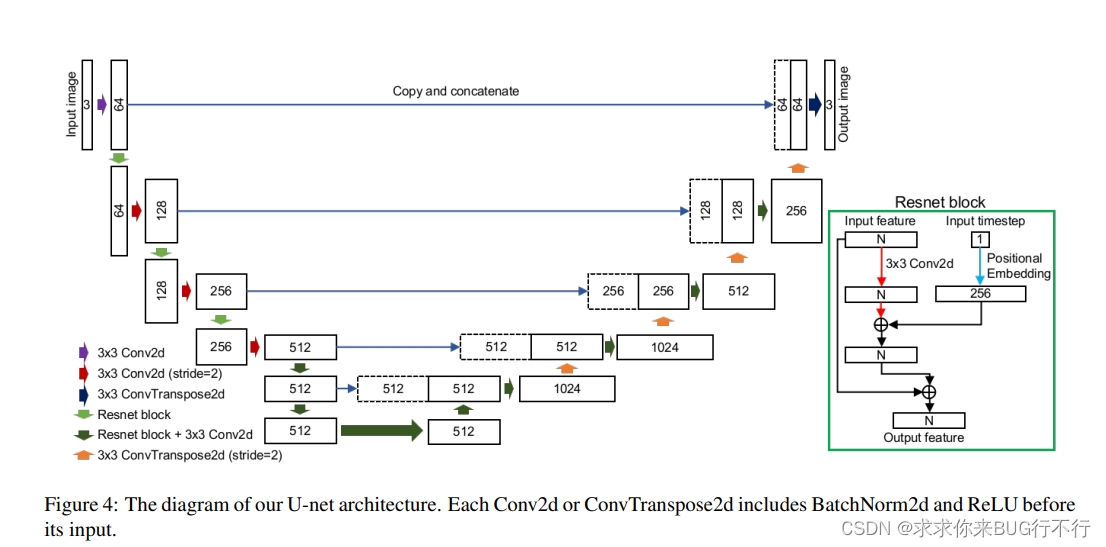
【深度学习】UNIT-DDPM核心讲解
文章目录 大致介绍:扩散损失:转换损失:循环一致性损失:推理过程:优缺点: 参考文章: https://blog.csdn.net/ssshyeong/article/details/127210086 这篇文章对整个文章 UNIT-DDPM: UNpaired Imag…...

Java 线程的优先级
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开兴好久好久😎 📚系列专栏:Java全栈,…...

金融数学方法:牛顿法
目录 1.牛顿法1.1 牛顿法介绍1.2 算法步骤 2. 具体算例3.总结 1.牛顿法 1.1 牛顿法介绍 牛顿法(Newton’s method),也被称为牛顿-拉夫森方法(Newton-Raphson method),是一种用于数值逼近根的迭代方法。它是…...

MongoTemplate | 多条件查询
MongoTemplate查询 Resource private MongoTemplate mongoTemplate;public <T> List<T> getDataList(String param1, Long param2, Class<T> clazz) {// 构建queryQuery query constructQuery(param1, param2);// 查询return mongoTemplate.find(query, cl…...

优秀程序员是怎么思考的?
首发日更公 Z 号:十二又十三 作为一名优秀的程序员,思考是我们工作中最重要的一部分。它不仅能够帮助我们解决问题,还能够提升我们的技术水平和职业发展。那么,优秀程序员是如何思考的呢?本文将为您介绍一个思考框架和…...

【juc】countdownlatch实现游戏进度
目录 一、截图示例二、代码示例 一、截图示例 二、代码示例 package com.learning.countdownlatch;import java.util.Arrays; import java.util.Random; import java.util.concurrent.CountDownLatch; import java.util.concurrent.ExecutorService; import java.util.concurr…...

Spring Webflux HttpHandler源码整理
HttpHandler的构造 自动启动配置类:HttpHandlerAutoConfigurationBean public HttpHandler httpHandler(ObjectProvider<WebFluxProperties> propsProvider) {HttpHandler httpHandler WebHttpHandlerBuilder.applicationContext(this.applicationContext).…...
Qt扩展-Advanced-Docking 简介及配置
Advanced-Docking 简介及配置 一、概述二、项目结构三、安装配置四、代码测试 一、概述 Advanced-Docking 是类似QDockWidget 功能的多窗口停靠功能的库。很像visual stdio 的 停靠功能,这个库对于停靠使用的比较完善。很多的软件都使用了这个框架。 项目源地址&a…...

Decorator
Decorator 动机 在某些情况下我们可能会“过度地使用继承来扩展对象的功能”, 由于继承为类型引入的静态特质,使得这种扩展方式缺乏灵活性; 并且随着子类的增多(扩展功能的增多),各种子类的组合ÿ…...
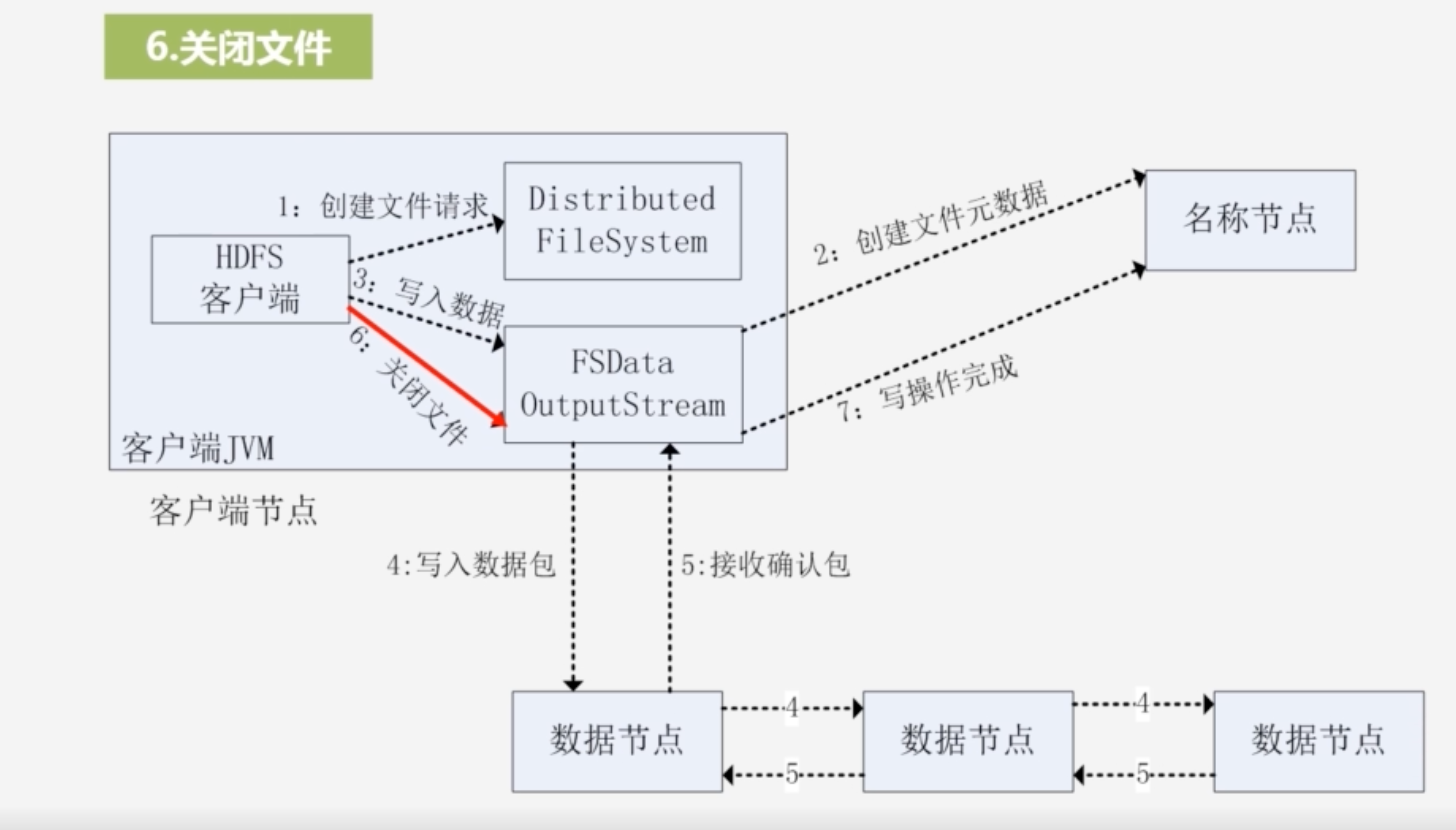
分布式文件系统HDFS(林子雨慕课课程)
文章目录 3. 分布式文件系统HDFS3.1 分布式文件系统HDFS简介3.2 HDFS相关概念3.3 HDFS的体系结构3.4 HDFS的存储原理3.5 HDFS数据读写3.5.1 HDFS的读数据过程3.5.2 HDFS的写数据过程 3.6 HDFS编程实战 3. 分布式文件系统HDFS 3.1 分布式文件系统HDFS简介 HDFS就是解决海量数据…...

CSS中:root伪类的使用
在CSS中,:root是一个伪类选择器,它选择的是文档树的根元素。在HTML文档中,这个根元素通常是<html>。:root伪类选择器常常被用于定义全局的CSS变量或者设置全局的CSS样式。 例如,你可以使用:root来定义一个全局的字体大小&a…...
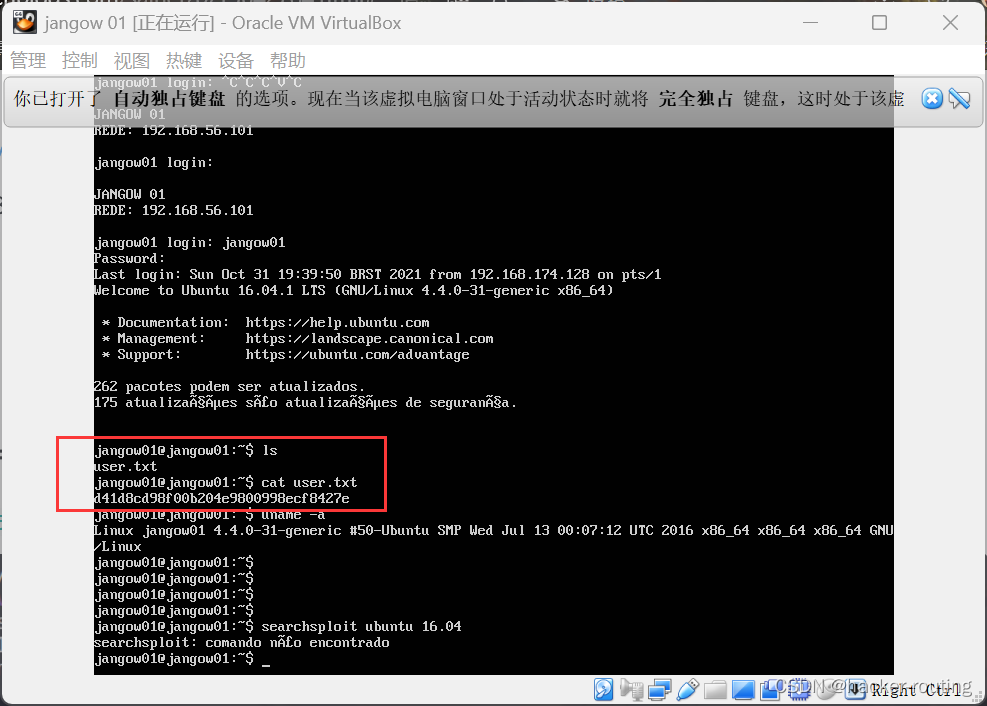
VulnHub JANGOW
提示(主机ip分配问题) 因为直接在VulnHub上下载的盒子,在VMware上打开,默认是不分配主机的 所以我们可以在VirtualBox上打开 一、信息收集 发现开放了21和80端口,查看一下80端口 80端口: 检查页面后发现…...

OpenMesh 获取网格面片各个顶点
文章目录 一、简介二、实现代码三、实现效果一、简介 OpenMesh中有很多循环器,这里便是其中一种面顶点循环器,以此来获得面片的各个顶点。 二、实现代码 #define _USE_MATH_DEFINES #include <iostream> #include <unordered_map>...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
