【算法】算法设计与分析 课程笔记 第三章 动态规划
1.1 动态规划简介
1.1.1 引例
动态规划算法和分治法类似,基本思想也是将待求解问题分解成若干个子问题,子问题可以以继续拆分,直到问题规模达到临界条件即可。多说无益,举个例子来解释一下:
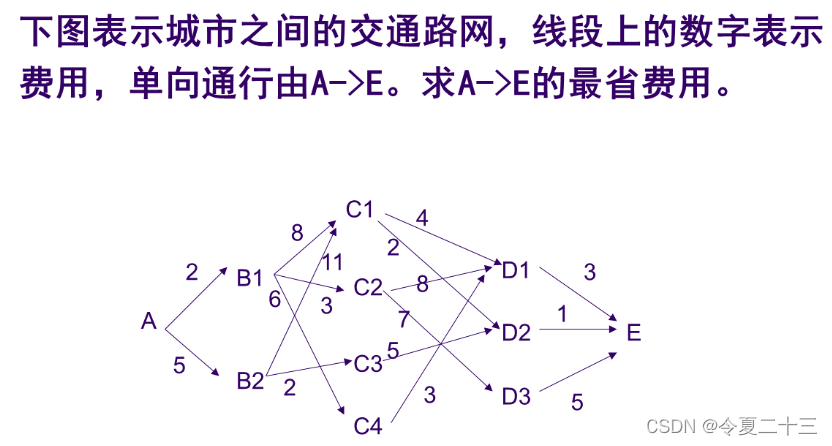
这其实是一个多阶段图求最短路的问题,路径大体上是 A→B→C→D→E,但是每到一个节点时就需要面临许多选择,所有选择中加起来最短的那一组就是要求的答案。
我们可以用动态规划的思想来分析这个问题,最开始从A出发,我们要选择一条最短的路,那么就可以把这个大问题先分成两个:从A到B和从B到E,这样就把大问题拆成两个小问题了,接下来,从A到B有两个选择,分别是B1和B2,它们和从B到E的路径相连,接下来就可以继续拆分,从B1到E和从B2到E又可以拆分成两个小问题,那就是从B到C和从C到E.......就这样一直拆下去,直到最后从D到E,这样再往回返回最短路径,直到得到整个问题的最短路径。
1.1.2 算法总体思想
从上面我们知道,动态规划算法也是不断地拆分问题,但是这里和之前的递归又有所不同,因为动态规划类的问题中,分解得到的子问题一般不会是相互独立的,也就是说有可能得到相同的子问题,所以在计算中,如果单单应用了递归,有些子问题就会被重复计算。
因此,适合使用动态规划来解决的问题一般都有下面两个性质:
1. 最优子结构性质
一个问题的最优解包含了其子问题的最优解。
2. 重叠子问题性质
在问题的求解过程中,很多子问题的解会被多次使用。
3.1 矩阵连乘问题
相关文章:

【算法】算法设计与分析 课程笔记 第三章 动态规划
1.1 动态规划简介 1.1.1 引例 动态规划算法和分治法类似,基本思想也是将待求解问题分解成若干个子问题,子问题可以以继续拆分,直到问题规模达到临界条件即可。多说无益,举个例子来解释一下: 这其实是一个多阶段图求最…...

贪心找性质+dp表示+矩阵表示+线段树维护:CF573D
比较套路的题目 首先肯定贪心一波,两个都排序后尽量相连。我一开始猜最多跨1,但其实最多跨2,考虑3个人的情况: 我们发现第3个人没了,所以可以出现跨2的情况 然后直接上dp,由 i − 1 , i − 2 , i − 3 i…...
小谈设计模式(17)—状态模式
小谈设计模式(17)—状态模式 专栏介绍专栏地址专栏介绍 状态模式关键角色上下文(Context)抽象状态(State)具体状态(Concrete State) 核心思想Java程序实现首先,我们定义一个抽象状态类 State,其中包含一个处理请求的方法 handleRe…...

Arm64体系架构-MPIDR_EL1寄存器
背景 在Arm64多核处理器中, 各核间的关系可能不同. 比如1个16 core的cpu, 每4个core划分为1个cluster,共享L2 cache. 当我们需要从core 0将任务调度出来时,如果优先选择core 1~3, 那么性能明显时优于其他core的. 那么操作系统怎么知道core之间这样的拓扑信息呢? Arm提供了MPID…...

MySQL支持哪些存储引擎
mysql支持九大存储引擎: 1)MYISAM存储引擎(优点:可被转换为压缩、只读表来节省空间。) 它管理的表具有以下特征: 使用三个文件表示每个表 格式文件-存储表结构的定义(mytable.frm) 数据文件-存…...

ElementUI结合Vue完成主页的CUD(增删改)表单验证
目录 一、CUD ( 1 ) CU讲述 ( 2 ) 编写 1. CU 2. 删除 二、验证 前端整合代码 : 一、CUD 以下的代码基于我博客中的代码进行续写 : 使用ElementUI结合Vue导航菜单和后台数据分页查询 ( 1 ) CU讲述 在CRUD操作中,CU代表创建(Create)…...
Flutter开发笔记 —— 语音消息功能实现
前言 最近在开发一款即时通讯(IM)的聊天App,在实现语音消息功能模块后,写下该文章以做记录。 注:本文不提供相关图片资源以及IM聊天中具体实现代码,单论语音功能实现思路 需求分析 比起上来直接贴代码,我们先来逐步…...
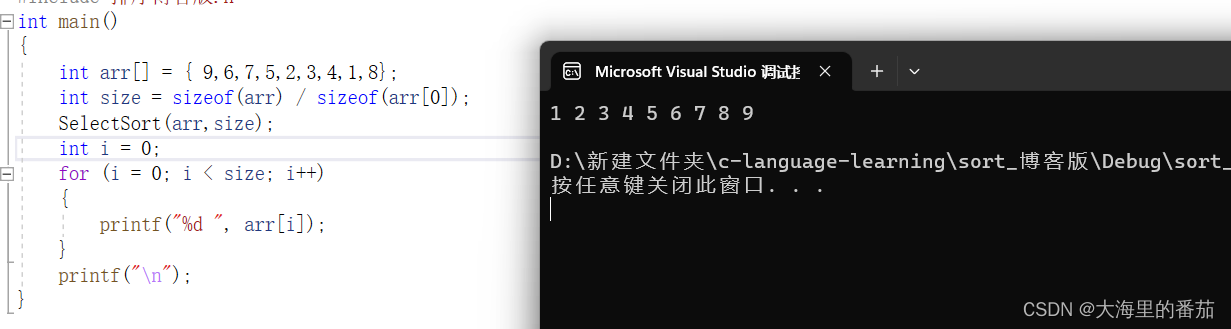
冒泡排序和选择排序
目录 一、冒泡排序 1.冒泡排序的原理 2.实现冒泡排序 1.交换函数 2.单躺排序 3.冒泡排序实现 4.测试 5.升级冒泡排序 6.升级版代码 7.升级版测试 二、选择排序 1.选择排序的原理 2.实现选择排序 1.单躺排序 2.选择排序实现 3.测试 4.修改 5.测试 一、冒泡排序…...
【深度学习】UNIT-DDPM核心讲解
文章目录 大致介绍:扩散损失:转换损失:循环一致性损失:推理过程:优缺点: 参考文章: https://blog.csdn.net/ssshyeong/article/details/127210086 这篇文章对整个文章 UNIT-DDPM: UNpaired Imag…...

Java 线程的优先级
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开兴好久好久😎 📚系列专栏:Java全栈,…...

金融数学方法:牛顿法
目录 1.牛顿法1.1 牛顿法介绍1.2 算法步骤 2. 具体算例3.总结 1.牛顿法 1.1 牛顿法介绍 牛顿法(Newton’s method),也被称为牛顿-拉夫森方法(Newton-Raphson method),是一种用于数值逼近根的迭代方法。它是…...

MongoTemplate | 多条件查询
MongoTemplate查询 Resource private MongoTemplate mongoTemplate;public <T> List<T> getDataList(String param1, Long param2, Class<T> clazz) {// 构建queryQuery query constructQuery(param1, param2);// 查询return mongoTemplate.find(query, cl…...

优秀程序员是怎么思考的?
首发日更公 Z 号:十二又十三 作为一名优秀的程序员,思考是我们工作中最重要的一部分。它不仅能够帮助我们解决问题,还能够提升我们的技术水平和职业发展。那么,优秀程序员是如何思考的呢?本文将为您介绍一个思考框架和…...

【juc】countdownlatch实现游戏进度
目录 一、截图示例二、代码示例 一、截图示例 二、代码示例 package com.learning.countdownlatch;import java.util.Arrays; import java.util.Random; import java.util.concurrent.CountDownLatch; import java.util.concurrent.ExecutorService; import java.util.concurr…...

Spring Webflux HttpHandler源码整理
HttpHandler的构造 自动启动配置类:HttpHandlerAutoConfigurationBean public HttpHandler httpHandler(ObjectProvider<WebFluxProperties> propsProvider) {HttpHandler httpHandler WebHttpHandlerBuilder.applicationContext(this.applicationContext).…...
Qt扩展-Advanced-Docking 简介及配置
Advanced-Docking 简介及配置 一、概述二、项目结构三、安装配置四、代码测试 一、概述 Advanced-Docking 是类似QDockWidget 功能的多窗口停靠功能的库。很像visual stdio 的 停靠功能,这个库对于停靠使用的比较完善。很多的软件都使用了这个框架。 项目源地址&a…...

Decorator
Decorator 动机 在某些情况下我们可能会“过度地使用继承来扩展对象的功能”, 由于继承为类型引入的静态特质,使得这种扩展方式缺乏灵活性; 并且随着子类的增多(扩展功能的增多),各种子类的组合ÿ…...
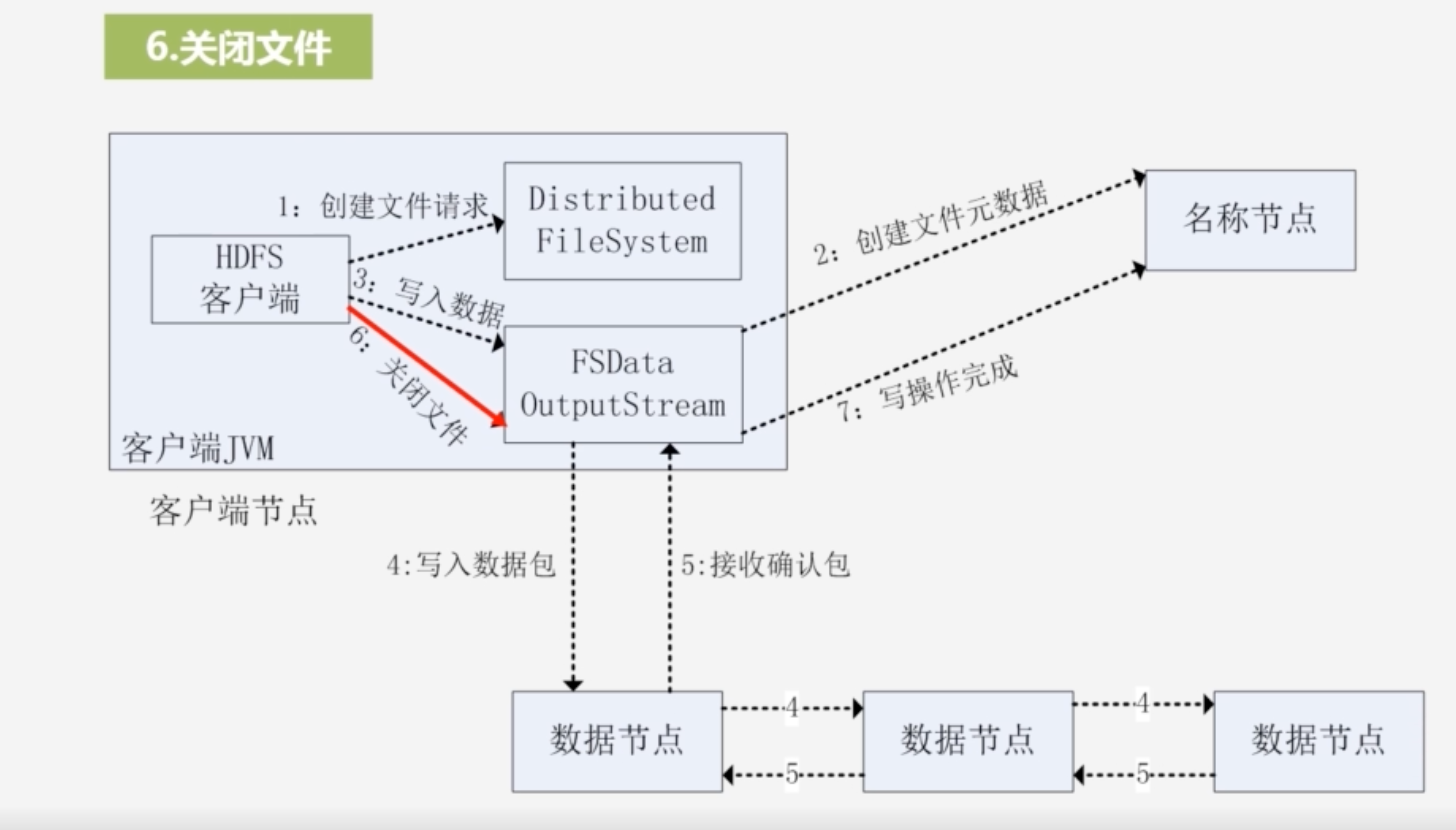
分布式文件系统HDFS(林子雨慕课课程)
文章目录 3. 分布式文件系统HDFS3.1 分布式文件系统HDFS简介3.2 HDFS相关概念3.3 HDFS的体系结构3.4 HDFS的存储原理3.5 HDFS数据读写3.5.1 HDFS的读数据过程3.5.2 HDFS的写数据过程 3.6 HDFS编程实战 3. 分布式文件系统HDFS 3.1 分布式文件系统HDFS简介 HDFS就是解决海量数据…...

CSS中:root伪类的使用
在CSS中,:root是一个伪类选择器,它选择的是文档树的根元素。在HTML文档中,这个根元素通常是<html>。:root伪类选择器常常被用于定义全局的CSS变量或者设置全局的CSS样式。 例如,你可以使用:root来定义一个全局的字体大小&a…...
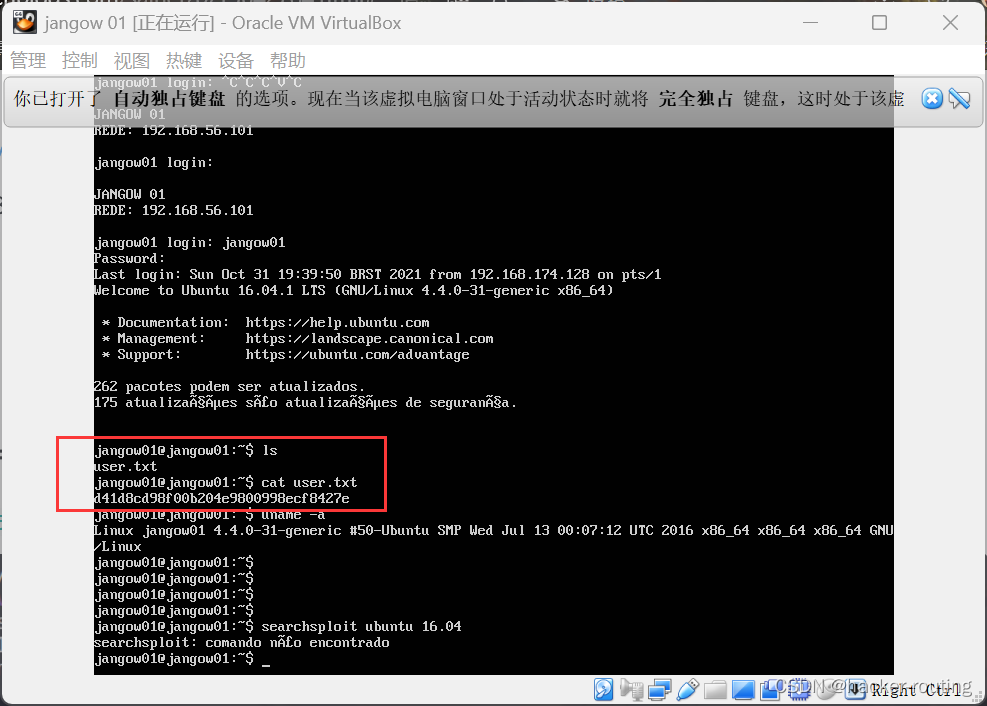
VulnHub JANGOW
提示(主机ip分配问题) 因为直接在VulnHub上下载的盒子,在VMware上打开,默认是不分配主机的 所以我们可以在VirtualBox上打开 一、信息收集 发现开放了21和80端口,查看一下80端口 80端口: 检查页面后发现…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
