整数保序的离散化(C/C++)
目录
1. 离散化的概念
1.1 离散化的运用思路
1.2 离散化的方法
1.2.1 排序
1.2.2 确定一个元素离散化后的结果
1.3 案例分析
1.3.1
1.3.2 区间和 (来源:Acwing)
1. 离散化的概念
离散化,把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。
例如:
原数据:1,999,100000,15;处理后:1,3,4,2;
原数据:{100,200},{20,50000},{1,400};
处理后:{3,4},{2,6},{1,5};
1.1 离散化的运用思路
以下离散化均指整数保序的离散化。
根据离散化的定义,我们能够发现需要如果数据需要做离散化的处理,那么该数据的值域跨度是非常大的,但是分布很稀疏。因为值域的跨度相当大,自身并不能作为数组的下标保存对应的属性。但是如果只需要这些数据的相对属性,那么就可以对数据进行离散化处理。
1.2 离散化的方法
这里只讲常用的方法:重复元素离散化的结果相同。
我们只需要确保两个事情不变:
首先:保证离散化之后的数据尽可能地小而且非负。
其次:离散后的数据要保持原本的大小关系,原本相等的也要保持相等,否则就是错误的离散。
因此,找出原数据在序列中的序位 (可以直接理解为排第几) 就是离散化的关键。
1.2.1 排序
离散化就是确定找出原数据在序列中排第几嘛,因此我们直接对其排序就好了,排完序便可直接根据该数据所在位置的下标确定其离散化的结果。但是显然单单排序是不够的,如果原数据中有重复元素,那么相同的数据就会有不同的离散化结果,这是不被允许的。因此,对排好序的数组我们还要进行去重的操作。
假设原数组为 array。
对于C++:排序用sort,去重用unique,删除末尾重复的元素用erase,即:
array.erase(unique(array.begin(), array.end()), array.end())

对于C语言:用 qsort 排序,用双指针算法去重就行。
1.2.2 确定一个元素离散化后的结果
比如:将数据:1 5 3 2 2 3,进行排序,去重,删除后,得到结果:1 2 3 5,比如我们想要知道 5 离散化后的结果是多少,该怎么做呢?答案就是二分查找哦。5 对应的下标就是 5 离散化的结果。这里就是标准的二分查找模板。
二分查找请参考:http://t.csdn.cn/CVAGj
int binary_search1(int* nums, int numsSize, int target)
{int l = 0, r = numsSize - 1;while (l < r){int mid = l + r >> 1;if (nums[mid] >= target){r = mid;}else{l = mid + 1;}}return l;
}1.3 案例分析
1.3.1
题目描述:
现有数列 A1,A2,A3 ··· ,An,数列中可能有重复元素。现在要求输出该数列的离散化数列,重复元素离散化后的数字相同。
输入:
第一行,一个整数 n (1 <= n <= 10 ^ 5)
第二行,n个整数整数,每个整数的取值为:[-10^9, 10^9]。
输出:
一行,包括 n 个整数。表示数列对应的离散化数列,重复元素离散化后的数字相同。
样例输入:
6
1 23424 242 65466 242 0
样例输出:
1 3 2 4 2 0
int binary_search1(vector<int>& nums, int target)
{int l = 0, r = nums.size() - 1;while (l < r){int mid = l + r >> 1;if (nums[mid] >= target){r = mid;}else{l = mid + 1;}}return l;
}int main()
{vector<int> array;vector<int> a;int n;cin >> n;int num;for (int i = 0; i < n; i++){scanf("%d", &num);array.push_back(num);a.push_back(num);}//排序sort(array.begin(), array.end());//去重和删除array.erase(unique(array.begin(), array.end()), array.end());for (int i = 0; i < a.size(); i++){int ret = binary_search1(array, a[i]);cout << ret << " ";}cout << endl;system("pause");return 0;
}
1.3.2 区间和 (来源:Acwing)
假定有一个无限长的数轴,数轴上每个坐标的数都是0.
现在我们首先进行 n 次操作,每次操作将某一位置 x 上的数加上 c 。
接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l, r] 之间所有数的和。
输入格式:
第一行包含两个整数 n 和 m。
接下来 n 行,包含两个整数 x 和 c。
再接下来 m 行,每行包含两个整数l 和 r。
输出格式:
共 m 行,每行输出一个询问中所求的区间内数字和。
数据范围:
-10 ^ 9 <= x <= 10 ^ 9 ,
1 <= n , m <= 10 ^ 5 ,
-10 ^ 9 <= l <= r <= 10 ^ 9 ,
-10000 <= c <= 10000
const int N = 300010;//这里用来存在c的位置加上x 和每一次询问的区间,当然也可以用结构体
typedef pair<int, int> PI;//在x的位置加上c不止一次,数组存
vector<PI> add;
//询问的区间不止一次,数组存
vector<PI> query;
//存所有添加的值c,需要离散化
vector<int>alls;
//保存离散化后的结果
int a[N];
//求区间和会用到前缀和的,创建一个前缀和数组
int s[N];int n, m;//这里离散化的值是从1开始的,为了对应求前缀和时也是从1开始
int binary_search1(int target)
{int l = 0, r = alls.size() - 1;while (l < r){int mid = l + r >> 1;if (alls[mid] >= target){r = mid;}else{l = mid + 1;}}return l + 1;
}int main()
{cin >> n >> m;for (int i = 0; i < n; i++){int x, c;cin >> x >> c;//记录每一次添加的位置和值add.push_back({ x,c });//加上c的位置x是需要离散化的alls.push_back(x);}//m次询问for (int i = 0; i < m; i++){int l, r;cin >> l >> r;//记录每一次询问query.push_back({ l,r });//输入的区间同样需要离散化alls.push_back(l);alls.push_back(r);}//排序,去重,删除sort(alls.begin(), alls.end());alls.erase(unique(alls.begin(), alls.end()), alls.end());for (pair<int, int> i : add){//将x位置加上c的x进行离散化int x = binary_search1(i.first);//a数组中的下标就代表离散化的值哈,值代表x的位置a[x] += i.second;}//前缀和处理for (int i = 1; i <= alls.size(); i++){s[i] = s[i - 1] + a[i];}//处理询问for (pair<int, int> i : query){int l = binary_search1(i.first);int r = binary_search1(i.second);cout << s[r] - s[l - 1] << endl;}return 0;
}
相关文章:

整数保序的离散化(C/C++)
目录 1. 离散化的概念 1.1 离散化的运用思路 1.2 离散化的方法 1.2.1 排序 1.2.2 确定一个元素离散化后的结果 1.3 案例分析 1.3.1 1.3.2 区间和 (来源:Acwing) 1. 离散化的概念 离散化,把无限空间中有限的个体映射到有限的…...

python--排序总结
1.快速排序 a.原理 快速排序的基本思想是在待排序的 n 个元素中任取一个元素(通常取第一个元素)作为基准,把该元素放人最终位置后,整个数据序列被基准分割成两个子序列,所有小于基准的元素放置在前子序列中࿰…...

进化的隐藏水印:深度学习提升版权保护的鲁棒性
一、前言 过去几年,以网络视频为代表的泛网络视听领域的崛起,是互联网经济飞速发展最为夺目的大事件之一。泛网络视听领域不仅是21世纪以来互联网领域的重要基础应用、大众文化生活的主要载体,而且在推动中国经济新旧动能转化方面也发挥了重…...
Jenkins配置项目教程
在上一篇[Jenkins的使用教程](https://blog.csdn.net/weixin_43787492/article/details/129028131?spm1001.2014.3001.5501)中我介绍了如何创建一个项目 Jenkins在创建项目中提供了很多功能供我们选择,这里我将对配置项目做一个较完整的介绍Jenkins配置项目0、所有…...

C++多继承,虚继承部分总结与示例
tags: C OOP 写在前面 写一下多继承, 虚继承的一些部分, 包括一些例子. 多继承 简介 多继承是指从多个直接基类中产生派生类的能力. 多继承的派生类继承了所有父类的属性, 所以会带来一些复杂的问题. 示例1: 多继承用法与调用顺序 #include <string> #include <…...
程序员35岁以后就没有出路了吗?听听京东10年测开的分析
国内的互联网行业发展较快,所以造成了技术研发类员工工作强度比较大,同时技术的快速更新又需要员工不断的学习新的技术。因此淘汰率也比较高,超过35岁的基层研发类员工,往往因为家庭原因、身体原因,比较难以跟得上工作…...
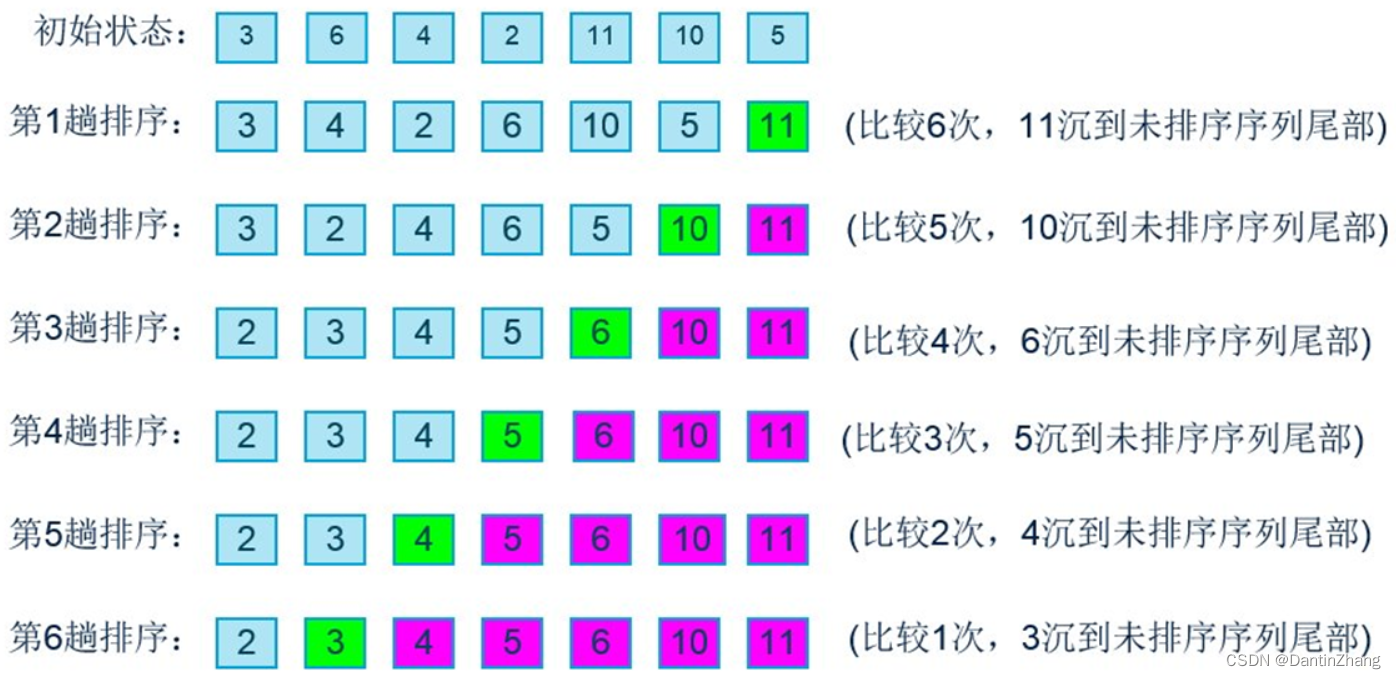
数据结构(六):冒泡排序、选择排序、插入排序、希尔排序、快速排序
数据结构(六)一、大O表示法二、冒泡排序三、选择排序一、大O表示法 在计算机中采用粗略的度量来描述计算机算法的效率,这种方法被称为“大O”表示法。 我们判断一个算法的效率,不能只凭着算法运行的速度,因为随着数据…...
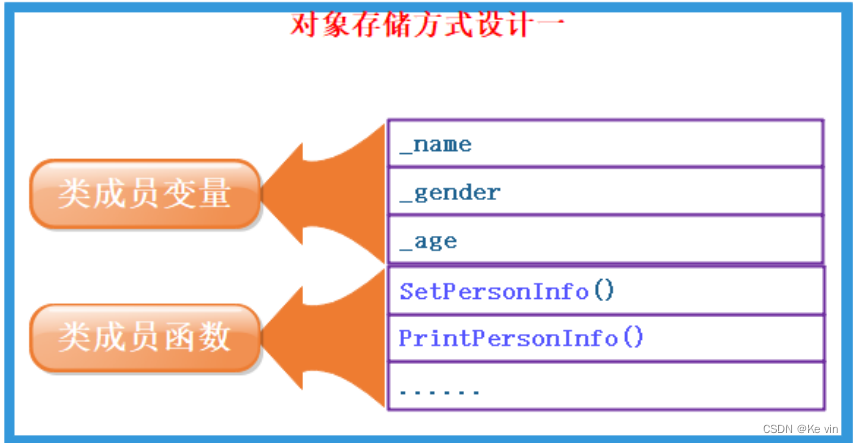
C++之类与对象(上)
目录 一、类的定义 二.类的访问限定及封装 1.访问限定 2.封装 三.类的作用域和实例化 2.类的实例化 四.类的对象大小的计算 1.类成员存储方式 2.结构体内存对齐规则 五.类成员函数的this指针 1.this指针的引出 2.this指针的特性 3.C语言和C实现Stack的对比 一、类的定义 class …...

Java岗面试题--Java并发 计算机网络(日积月累,每日三题)
目录1. 面试题一:在 Java 程序中怎么保证多线程的运行安全?1.1 追问一:Java 线程同步的几种方法?2. 面试题二:JMM3. 面试题三:计算机网络的各层协议及作用?1. 面试题一:在 Java 程序…...
三菱FX3U与威纶MT8071IP走RS422通讯
一、准备工作 1.需要工具: 电脑一台、PLC:三菱FX3U一个、触摸屏:威纶MT8071一个、 (三菱圆形编程口转USB)一根、触摸屏与电脑通讯线一根(T型口数据线)、PLC与触摸屏通讯线:电烙…...

给想考CISP的一点建议
如果你正在考虑参加CISP认证考试,以下是我对你的几点建议: 了解CISP考试: 在报名参加考试之前,要充分了解CISP认证考试的考试内容、考试形式、考试难度等相关信息,这有助于你制定更有效的备考计划。制定备考计划&…...
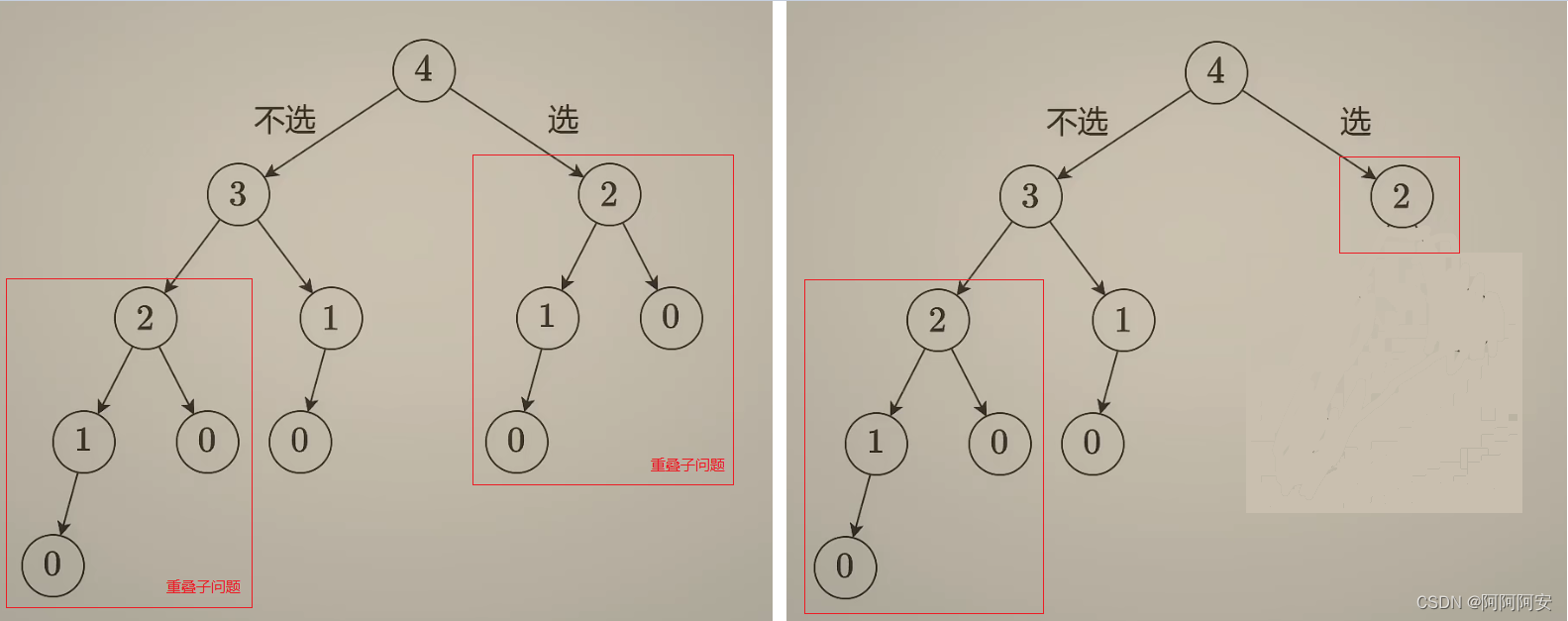
ACM 记忆化搜索
一.记忆化搜索概述 1.概念 搜索是一种简单有效但是效率又很低下的算法结构,其低效的原因主要在于存在很多重叠子问题。而记忆化搜索则是在搜索的基础上,利用数组来记录已经计算出来的重叠子问题状态,进行合理化的剪枝,从而降低时…...

spring框架常用注解简单说明
1、Configuration:标注在类上,相当于把当前类作为spring的xml配置文件中的; 2、Bean:标注在方法上,相当于spring配置文件中的; 3、Service:标注在类上,表明当前类是一个服务层的Be…...

2023-02-24 mysql/innodb-聚合-临时表避免OOM-使用磁盘文件-分析
摘要: mysql/innodb在执行聚合时, 当聚合的数据量太大时, 也就是临时表的大小超过tmp_table_size 限制时, 将进行写磁盘操作, 以避免OOM。 本文记录聚合数据写磁盘的操作。 参考: https://dev.mysql.com/doc/refman/5.7/en/server-system-variables.html#sysvar_tmp_table_…...
cracklib与libpwquality 评估密码的安全性
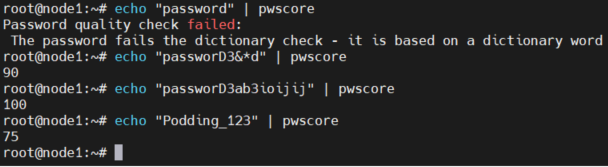
一、cracklib 检测密码强弱linux中采用pam pam_cracklib module来实现对密码强度的检测,可以通过配置让linux系统自动检测用户的密码是否为弱密码。yuminstall cracklib # centos apt-get install libcrack2 # ubuntu # 如果需要依赖此库做开发的话需要安装这个 y…...

【Java】保证并发安全的三大特性
一、并发编程三大特性的定义和由来 并发编程这三大特性就是为了在多个线程交替执行任务的过程中保证线程安全性。 二、为什么会出现线程不安全的现象呢? 接下来我们从这三个特性切入来介绍线程不安全的原因。 1.原子性: 一组操作要么全部执行&#…...
如何优雅的用golang封装配置项(Functional Options)
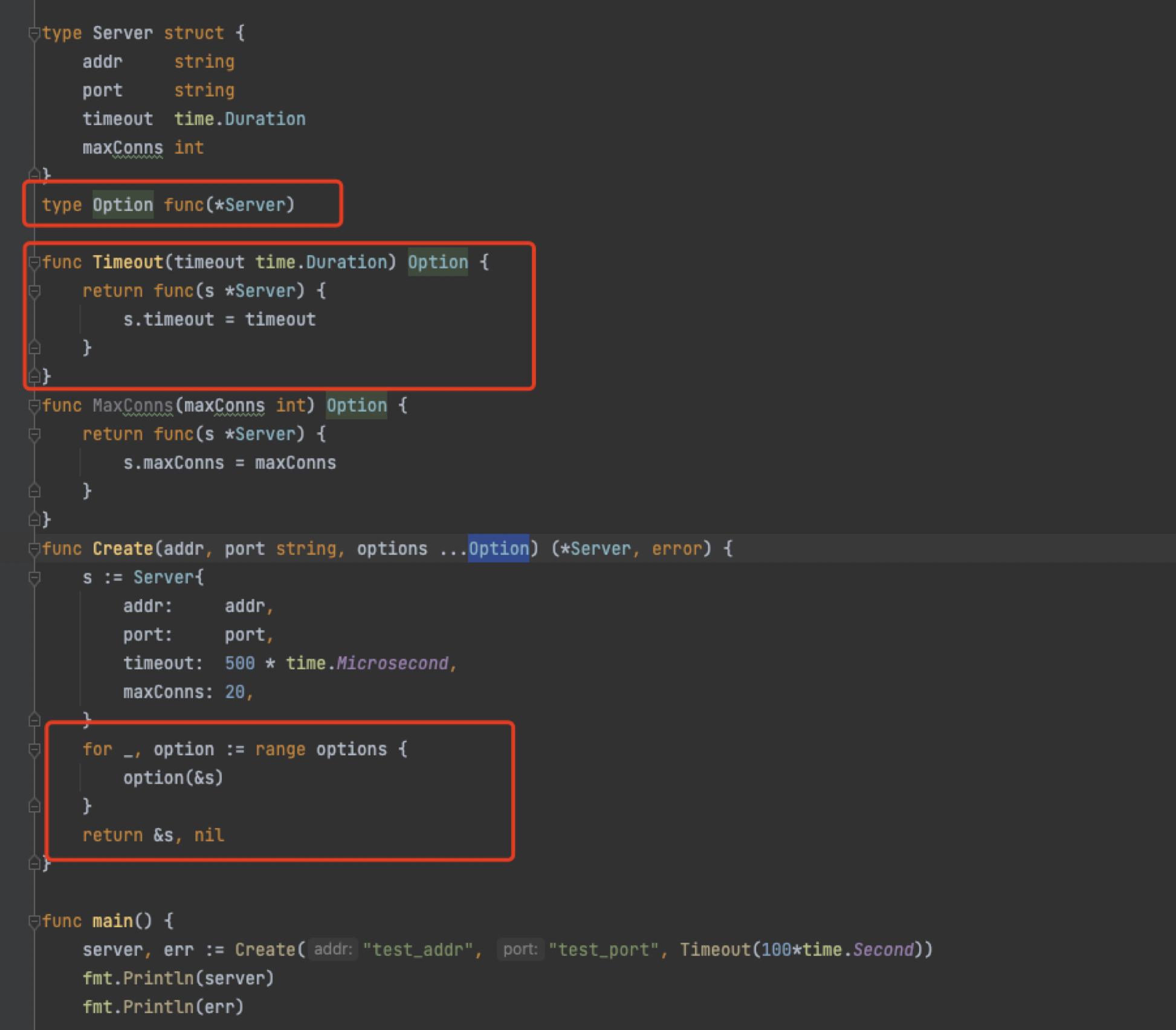
导读 最近要封装一个公共服务,涉及到配置项的地方总是找不到合理的方案,后来看了一下grpc在配置方面的封装,了解到原来是golang特有的Functional Options编程模式,今天分享给大家,希望你能用到,咱们直接来看…...

Springboot 使用thymeleaf 服务器无法加载resources中的静态资源异常处理
目录一、异常错误二、原因三、解决方法方法1. 将无法编译的静态资源放入可编译目录下方法2. 重新编译项目加载资源方法3. 修改pom.xml资源配置文件方法4. 不连接远程数据库启动,使用本地数据库一、异常错误 Springboot使用thymeleaf,并连接远程数据库启…...

服务端IOS订阅类型支付接入详细说明与注意事项
一、说明 由于本人在开发ios订阅类型支付接入的时候,遇到了很多坑,也查了不少资料,逐步完善了整个ios订阅支付服务端接入的功能,在这里写下总结和一些注意事项的记录,方便未来需要重新接入或者避免一些不必要的坑,这里…...
【剑指Offer】重建二叉树(递归+迭代)
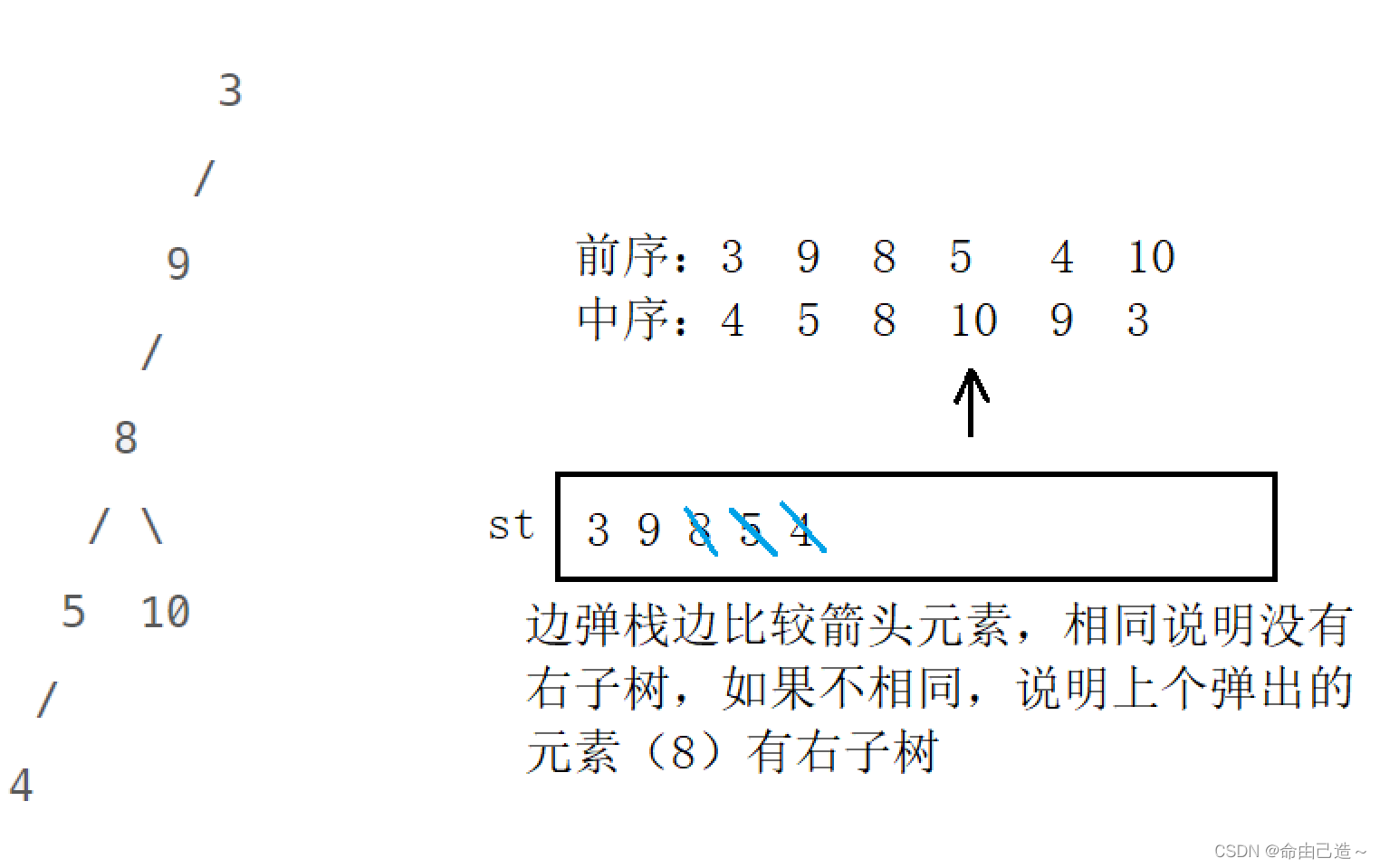
重建二叉树一、递归法二、迭代法题目链接 题目描述: 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 示例 1: Input: preorder [3,9,20,15,7], inorder [9,3,15,…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
