当前位置： 首页 > news >正文

常见排序算法Java版（待续）

news 文章来源：https://blog.csdn.net/qq_58616732/article/details/133720862 2025/4/8 20:24:07

  1. 冒泡排序O(n^2)

    public class Main {public static void main(String[] args) {Random random = new Random();int[] nums = new int[]{random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100)};for (int i = nums.length - 1; i >= 0; i--) {for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {int temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}}for (int num : nums) {System.out.print(num + " ");}}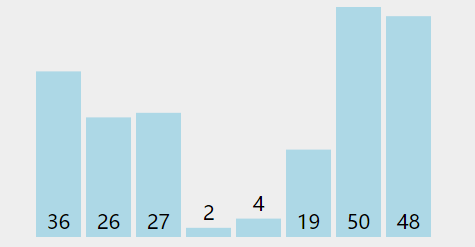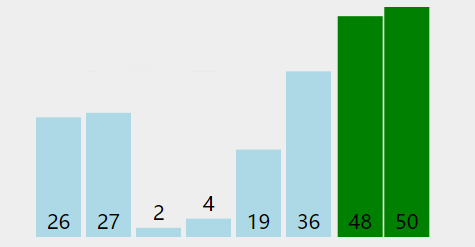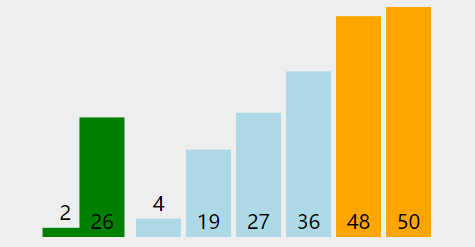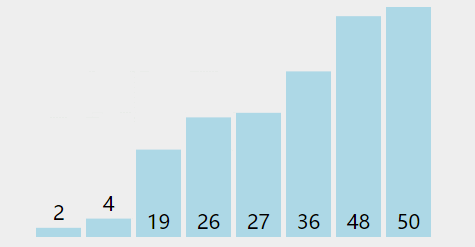
}

    冒泡排序动图演示

  2. 选择排序O(n^2),

    public class Main {public static void main(String[] args) {Random random = new Random();int[] nums = new int[]{random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100)};int index;for (int i = 0; i < nums.length; i++) {index = i;//每一轮记录最小值的索引for (int j = i + 1; j < nums.length; j++) {if (nums[j] < nums[index]) {index = j;}}if (index != i) {int temp = nums[i];nums[i] = nums[index];nums[index] = temp;}}for (int num : nums) {System.out.print(num + " ");}}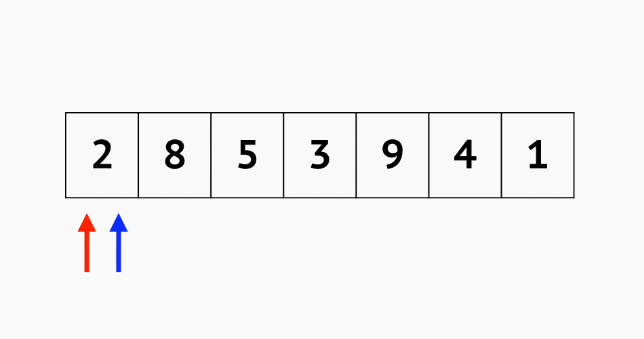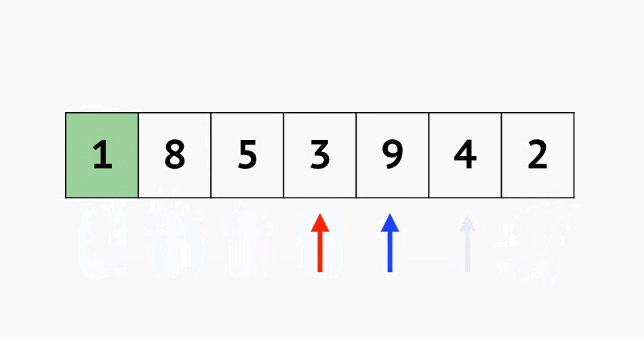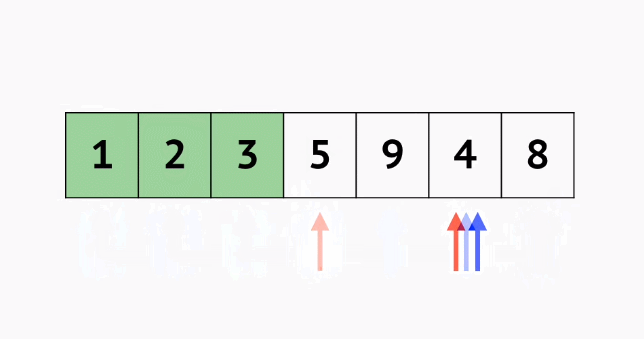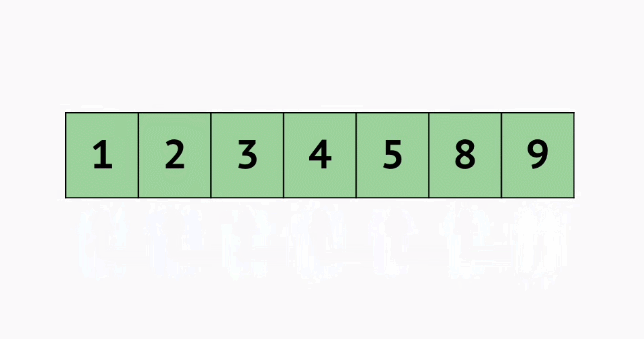
}

    排序算法——选择排序_选择排序语句-CSDN博客

  3. 插入排序O(n^2)

    public class Main {public static void main(String[] args) {Random random = new Random();int[] nums = new int[]{random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100)};int index;for (int i = 1; i < nums.length; i++) {int rec = nums[i];index = i;for (int j = i - 1; j >= 0; j--) {if (nums[j] > rec) {nums[index] = nums[j];index = j;} else {break;}}nums[index] = rec;}for (int num : nums) {System.out.print(num + " ");}}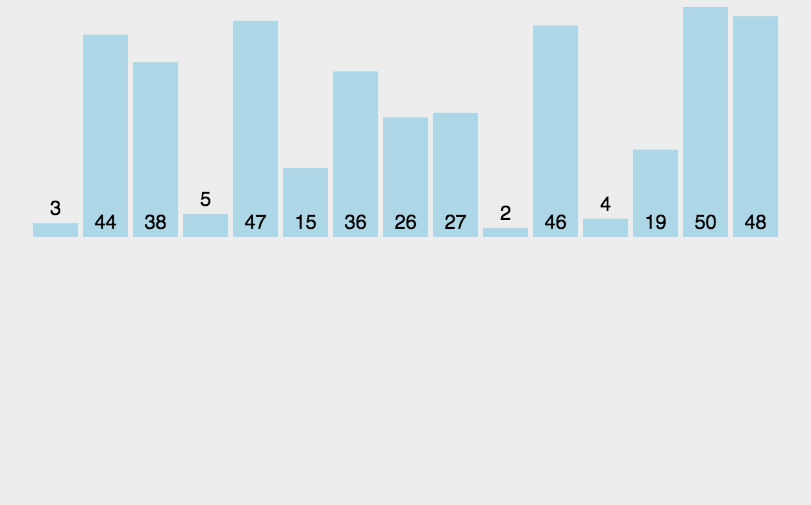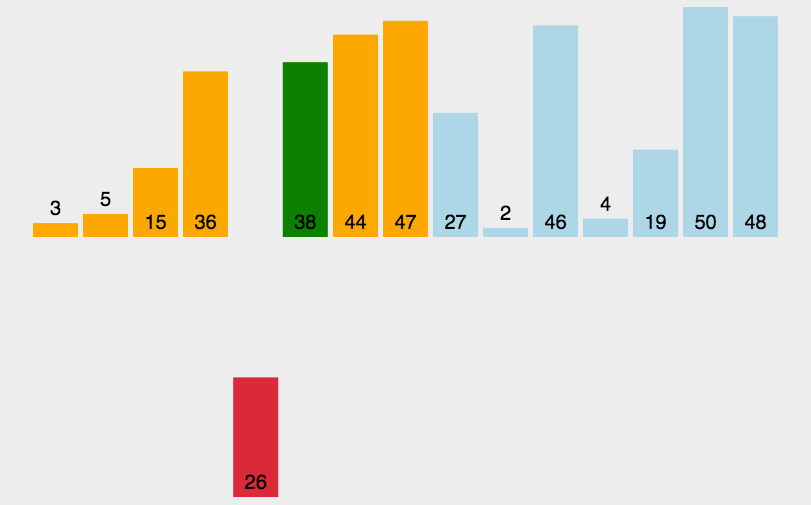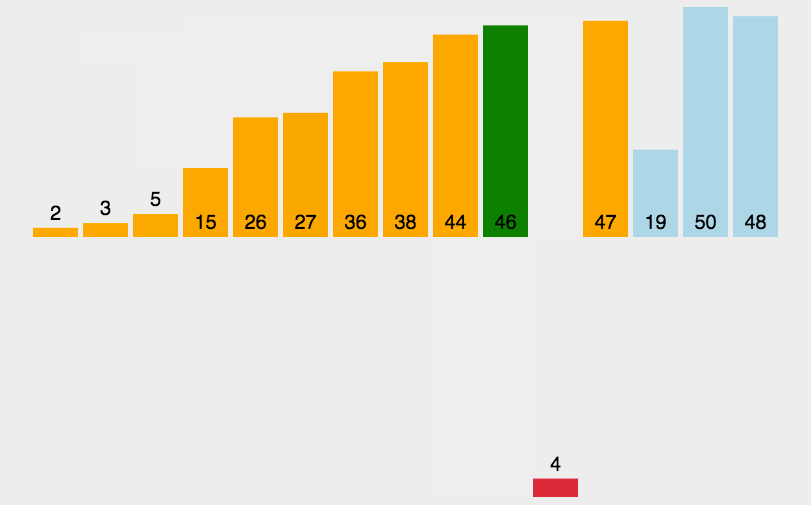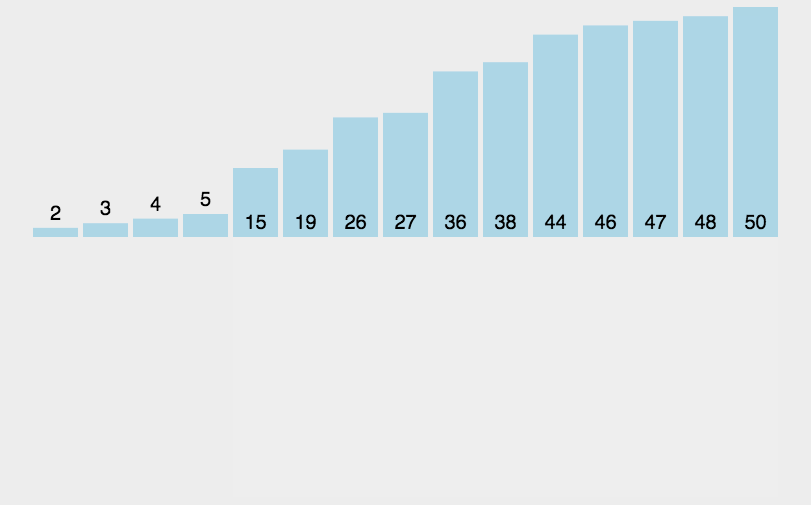
}

    img

相关文章：

常见排序算法Java版（待续）

冒泡排序O(n^2) public class Main {public static void main(String[] args) {Random random new Random();int[] nums new int[]{random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100), random.nextInt(100)};for (i…...

编程日记 2023/10/10 4:05:33

Jmeter 多实例压测

Apache JMeter 是一个开源的 Java 应用程序&#xff0c;用于性能测试和负载测试。它最初是为测试 Web 应用程序而创建的&#xff0c;但现在已广泛用于测试各种不同类型的应用程序&#xff0c;包括数据库、消息队列、FTP 服务器等。JMeter 提供了丰富的功能&#xff0c;使您能够…...

编程日记 2023/10/10 4:03:31

线程安全问题 --- 内存可见性问题

小王学习录 本月鸡汤:什么是内存可见性问题引起内存可见性问题的原因如何解决内存可见性问题volatile使用规范编外: 工作内存(工作存储区)由前面文章介绍可以知道, 引起线程安全问题有 五个原因, 分别是: 线程抢占式执行, 随即调度(根本原因); 多个线程对同一变量执行 修改操…...

编程日记 2023/10/10 4:02:30

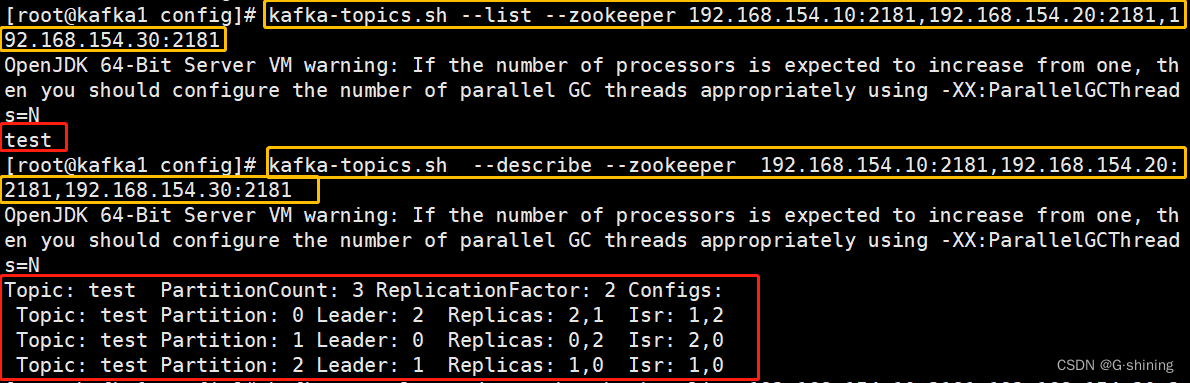
消息队列 Kafka

Kafka Kafka 是一个分布式的基于发布/订阅模式的消息队列&#xff08;MQ&#xff0c;Message Queue&#xff09;&#xff0c;主要应用于大数据实时处理领域 为什么使用消息队列MQ 在高并发环境下&#xff0c;同步请求来不及处理会发生堵塞&#xff0c;从而触发too many conne…...

编程日记 2023/10/10 4:01:29

抽象轻松的java-mybatis简单入门

第一步&#xff1a;用IDEA新建一个java包 第二步&#xff1a;在IDEA中添加数据库&#xff08;ps&#xff1a;自己百度&#xff09; 点击数据库 第二步&#xff0c;新建数据库 选择你使用的数据库 用户与密码根据自己的设置进行配置 为了更方便的查看数据库&#xff0c;可以像图…...

编程日记 2023/10/10 4:00:28

012-第二代硬件选型

第二代硬件选型 文章目录 第二代硬件选型项目介绍重新换平台缘由X86 && Arm 架构切换 ARM Linux 硬件选型系统确定Qt 版本确定总结一下 关键字&#xff1a; Qt、 Qml、 Arm、 X86、 linux 项目介绍 欢迎来到我们的 QML & C 项目&#xff01;这个项目结合了 QM…...

编程日记 2023/10/10 3:59:28

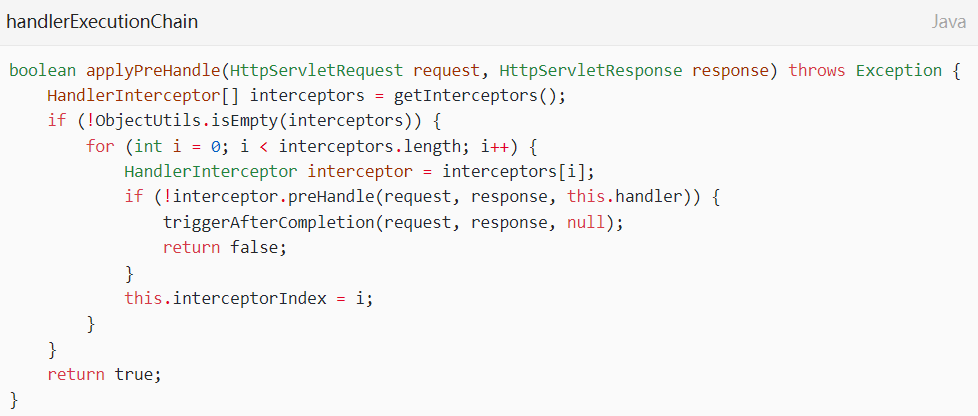
Spring中的设计模式

目录 工厂模式 组合模式 适配器模式 代理模式 单例模式 观察者模式 模板方法模式 责任链模式 Spring有着非常优雅的设计&#xff0c;很多地方都遵循SOLID原则&#xff0c;里面的设计模式更是数不胜数大概有以下几种&#xff1a; 工厂模式 所谓的工厂模式&#xff0c;核…...

编程日记 2023/10/10 3:58:27

软考 系统架构设计师系列知识点之软件质量属性（1）

这个十一注定是一个不能放松、保持“紧”的十一。由于报名了全国计算机技术与软件专业技术资格&#xff08;水平&#xff09;考试&#xff0c;11月4号就要考试&#xff0c;因此8天长假绝不能荒废&#xff0c;必须要好好利用起来。现在将各个核心知识点一一进行提炼并做记录。 所…...

编程日记 2023/10/10 3:57:26

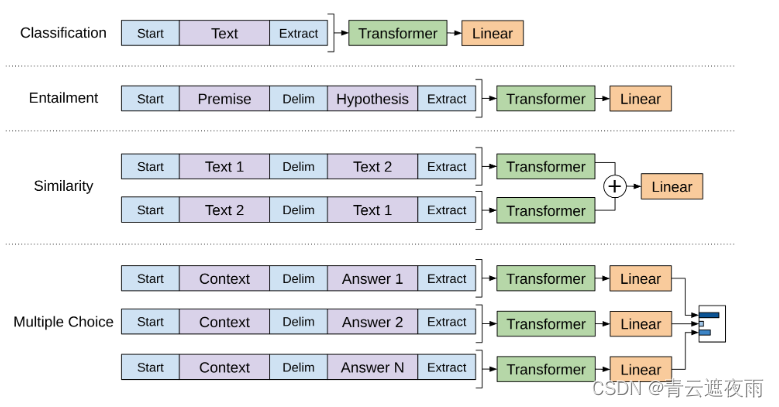
GPT系列论文解读：GPT-1

GPT系列 GPT&#xff08;Generative Pre-trained Transformer&#xff09;是一系列基于Transformer架构的预训练语言模型&#xff0c;由OpenAI开发。以下是GPT系列的主要模型&#xff1a; GPT&#xff1a;GPT-1是于2018年发布的第一个版本&#xff0c;它使用了12个Transformer…...

编程日记 2023/10/10 3:56:25

数学分析：含参变量的积分

同样很多收敛性的证明不是重点&#xff0c;但里面的知识还是需要适当掌握&#xff0c;知道中间的大致思考和解决路径即可。 本质还是极限的可交换性&#xff0c;求导可以换到积分里面去操作。 这里要注意变量的区别&#xff0c;首先积分的被积变量是x&#xff0c;但是函数的变量…...

编程日记 2023/10/10 3:55:24

关于一篇ElementUI之CUD+表单验证

目录 一.CUD增删改查简述 1.1.增删改功能实现 二.表单验证 前端所有代码&#xff1a; 好啦今天就分享到这了&#xff0c;希望能帮到你哦&#xff01;&#xff01;&#xff01; 以下的代码基于我博客中的代码进行续写 : 关于ElementUI之动态树数据表格分页实例 一.CUD增删改…...

编程日记 2023/10/10 3:54:23

VUE模板编译的实现原理

前言 在Vue.js 2.0中&#xff0c;模板编译是通过将模板转换为渲染函数来实现的。渲染函数是一个函数&#xff0c;它返回虚拟DOM节点&#xff0c;用于渲染实际的DOM。Vue.js的模板编译过程可以分为以下几个步骤&#xff1a; 将模板解析为抽象语法树&#xff08;AST&#xff09…...

编程日记 2023/10/10 3:53:22

基础算法之——【动态规划之路径问题】1

今天更新动态规划路径问题1&#xff0c;后续会继续更新其他有关动态规划的问题&#xff01;动态规划的路径问题&#xff0c;顾名思义&#xff0c;就是和路径相关的问题。当然&#xff0c;我们是从最简单的找路径开始&#xff01; 动态规划的使用方法&#xff1a; 1.确定状态并…...

编程日记 2023/10/10 3:52:21

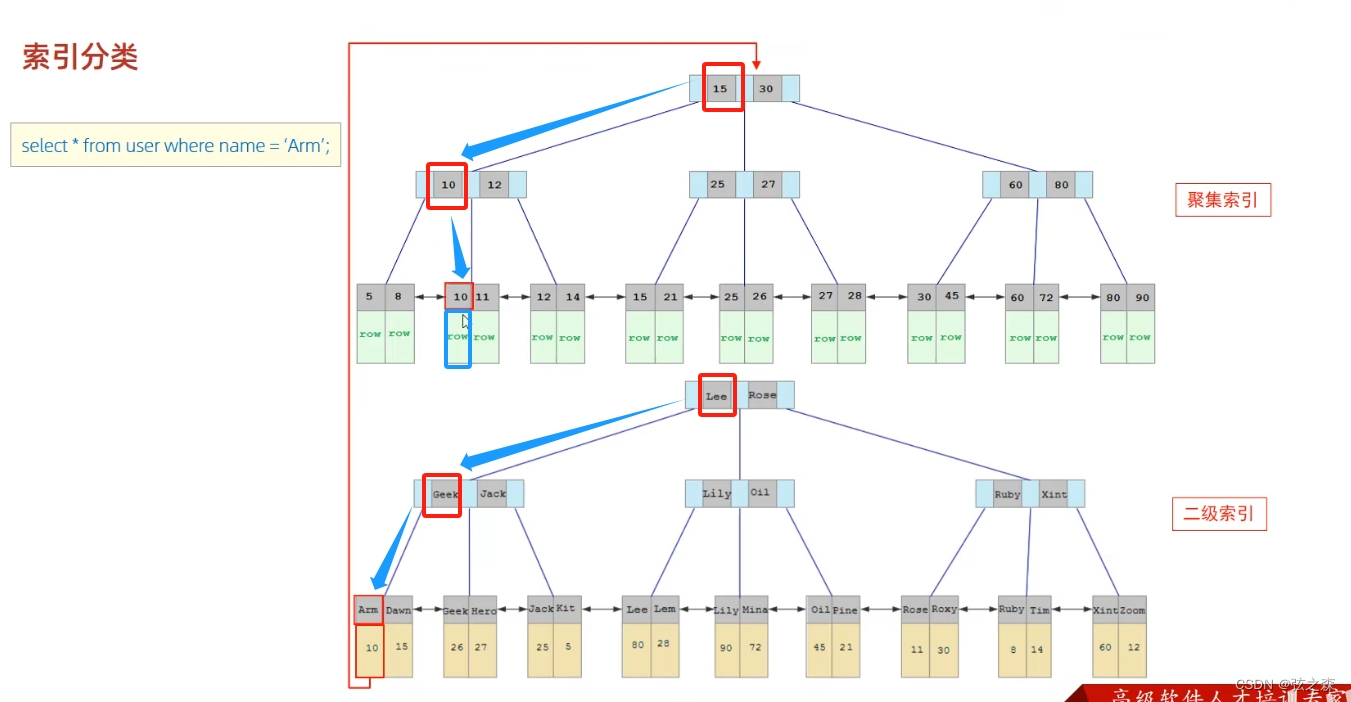
三十三、【进阶】索引的分类

1、索引的分类 &#xff08;1&#xff09;总分类 主键索引、唯一索引、常规索引、全文索引 &#xff08;2&#xff09;InnoDB存储引擎中的索引分类 2、 索引的选取规则(InnoDB存储引擎) 如果存在主键&#xff0c;主键索引就是聚集索引&#xff1b; 如果不存在主键&#xff…...

编程日记 2023/10/10 3:51:19

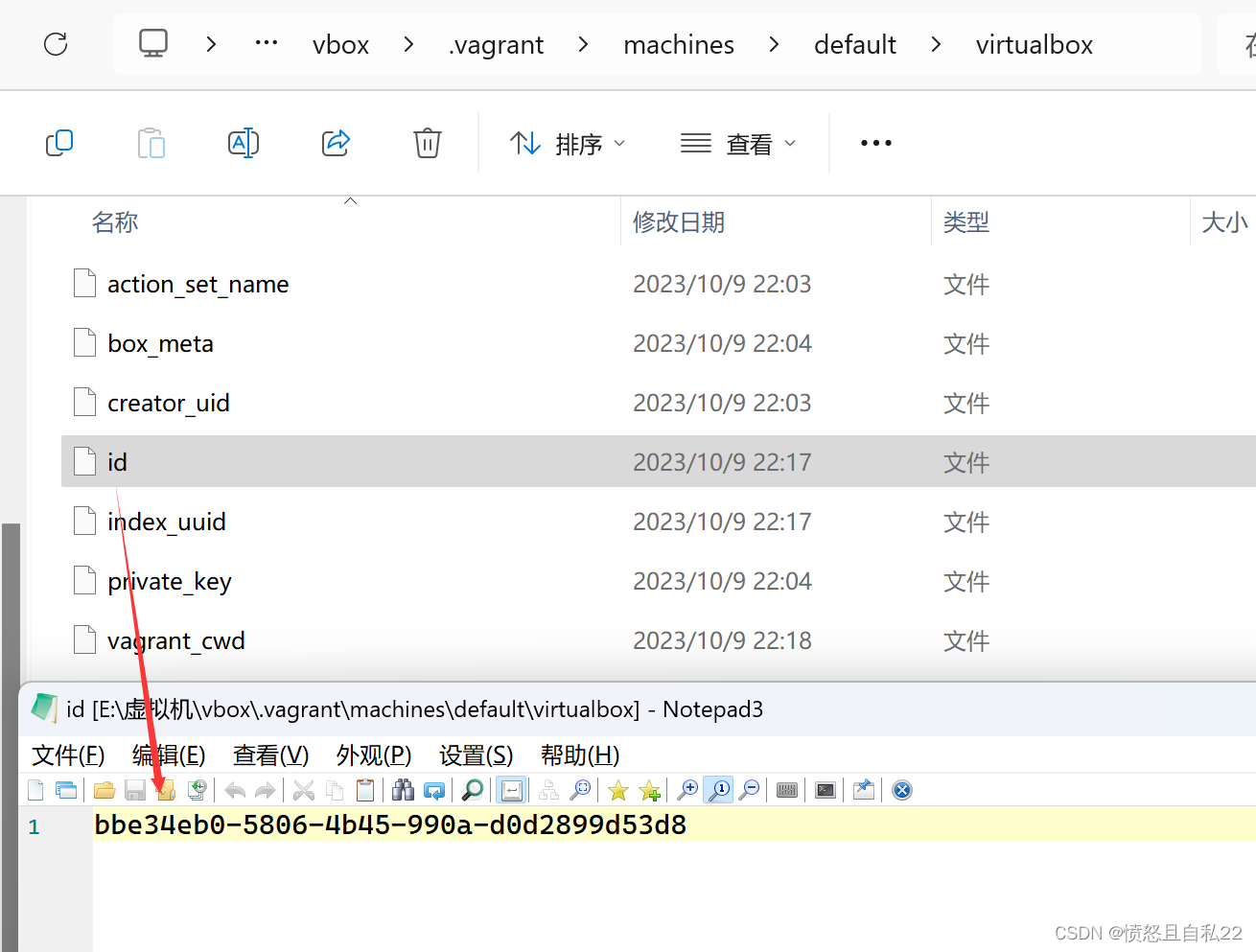
VBox启动失败、Genymotion启动失败、Vagrant迁移

VBox启动失败、Genymotion启动失败、Vagrant迁移 2023.10.9 最新版本vbox7.0.10、Genymotion3.5.0 Vbox启动失败 1、查看日志 Error -610 in supR3HardenedMainInitRuntime! (enmWhat4) Failed to locate ‘vcruntime140.dll’ 日志信息查看方法->找到虚拟机所在位置->…...

编程日记 2023/10/10 3:49:17

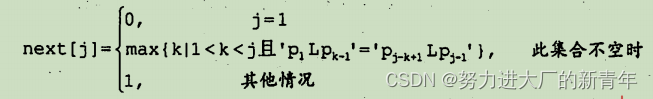
一篇短小精悍的文章让你彻底明白KMP算法中next数组的原理

以后保持每日一更&#xff0c;由于兴趣较多&#xff0c;更新内容不限于数据结构&#xff0c;计算机组成原理&#xff0c;数论&#xff0c;拓扑学......&#xff0c;所谓&#xff1a;深度围绕职业发展&#xff0c;广度围绕兴趣爱好。往下看今日内容 一.什么是KMP算法 KMP&#x…...

编程日记 2023/10/10 3:48:15

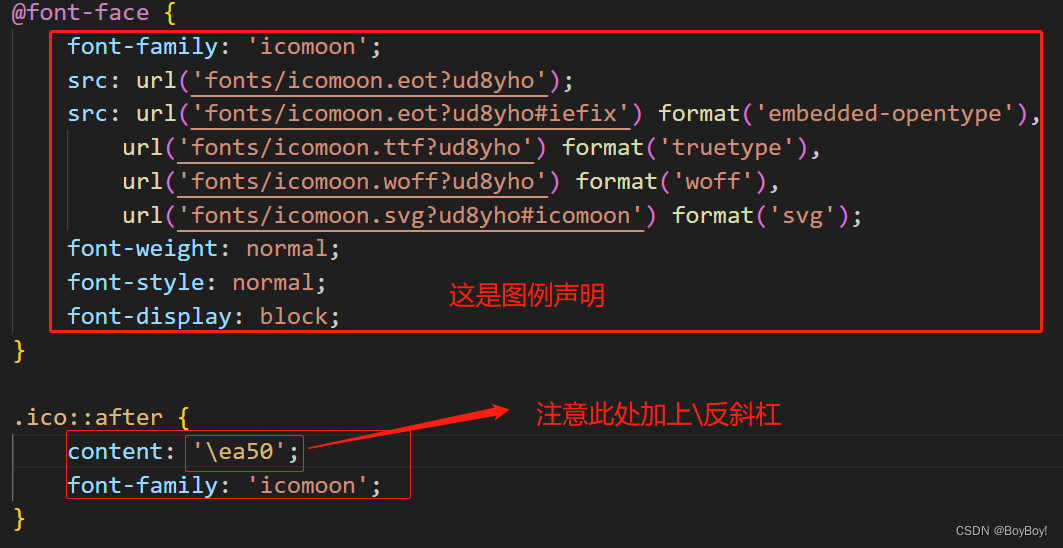
CSS盒子定位的扩张

定位的扩展 绝对定位&#xff08;固定定位&#xff09;会完全压住盒子 浮动元素不会压住下面标准流的文字&#xff0c;而绝对定位或固定位会压住下面标准流的所有内容 如果一个盒子既有向左又有向右&#xff0c;则执行左&#xff0c;同理执行上 显示隐藏 display: none&…...

编程日记 2023/10/10 3:46:13

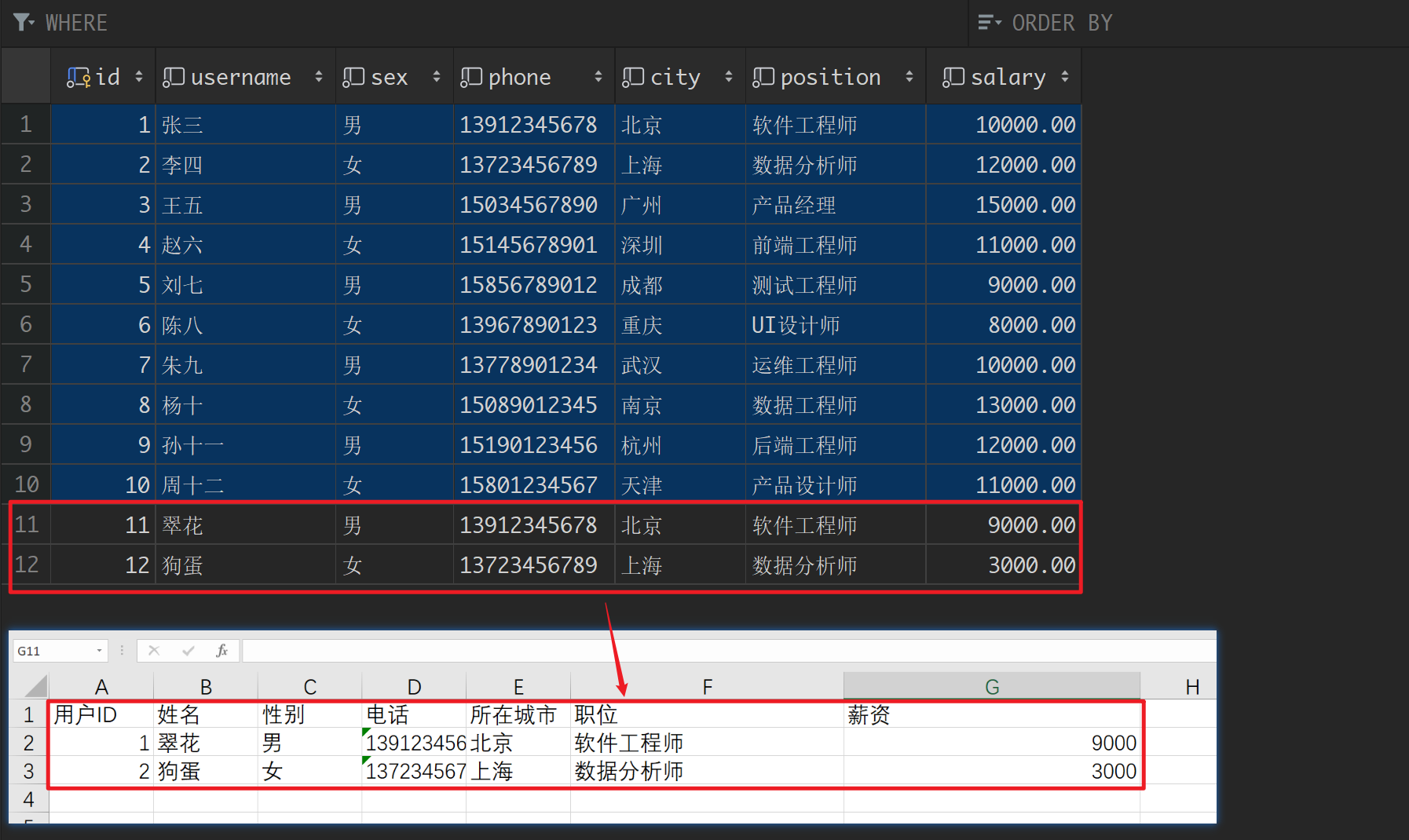
SpringBoot整合POI实现Excel文件读写操作

1.环境准备 1、导入sql脚本&#xff1a; create database if not exists springboot default charset utf8mb4;use springboot;create table if not exists user (id bigint(20) primary key auto_increment comment 主键id,username varchar(255) not null comment 用…...

编程日记 2023/10/10 3:45:13

从零开始的力扣刷题记录-第八十七天

力扣每日四题 129. 求根节点到叶节点数字之和-中等130. 被围绕的区域-中等437. 路径总和 III-中等376. 摆动序列-中等总结 129. 求根节点到叶节点数字之和-中等 题目描述&#xff1a; 给你一个二叉树的根节点 root &#xff0c;树中每个节点都存放有一个 0 到 9 之间的数字。 …...

编程日记 2023/10/10 3:44:12

【1】c++设计模式——＞UML类图的画法

UML介绍 UML:unified modeling language 统一建模语言 面向对象设计主要就是使用UML类图&#xff0c;类图用于描述系统中所包含的类以及他们之间的相互关系&#xff0c;帮助人们简化对系统的理解&#xff0c;他是系统分析和设计阶段的重要产物&#xff0c;也是系统编码和测试的…...

编程日记 2023/10/10 3:41:08

SAP UI5 指定 / 变更版本

SAP UI5 指定 / 变更版本 Currently, SAP Fiori tools support SAP Fiori elements and SAPUI5 freestyle projects with minimum SAPUI5 versions 1.65 or higher. In case there’s a need to test an existing projects with a lower SAPUI5 version, the following worka…...

编程日记 2023/10/10 3:40:07

SpringMVC中异常处理详解

单个控制器异常处理 // 添加ExceptionHandler&#xff0c;表示该方法是处理异常的方法&#xff0c;属性为处理的异常类ExceptionHandler({java.lang.NullPointerException.class,java.lang.ArithmeticException.class})public String exceptionHandle1(Exception ex, Model mo…...

编程日记 2023/10/10 3:39:07

PPT课件培训视频生成系统实现全自动化

前言 困扰全动自化的重要环节&#xff0c;AI语音合成功能&#xff0c;终于可以实现自动化流程&#xff0c;在此要感谢团队不懈的努力和韧性的精神&#xff01; 实现原理 请参照我的文章《Craneoffice云PPT课件培训视频生成系统》 基本流程 演示视频 PPT全自动 总结 过去实…...

编程日记 2023/10/10 3:38:05

Densenet---＞比残差力度更大 senet--＞本质抑制特征

...

编程日记 2023/10/10 3:37:04

基于腾讯云的OTA远程升级

一、OTA OTA即over the air,是一种远程固件升级技术&#xff0c;它允许在设备已经部署在现场运行时通过网络远程更新其固件或软件。OTA技术有许多优点&#xff0c;比如我们手机系统有个地方做了优化&#xff0c;使用OTA技术我们就不用召回每部手机&#xff0c;直接通过云端就可…...

编程日记 2023/10/10 3:36:02

如何在VS2022中进行调试bug，调试的快捷键，debug与release之间有什么区别

什么是bug 在学习编程的过程中&#xff0c;应该都听说过bug吧&#xff0c;那么bug这个词究竟是怎么来的呢&#xff1f; 其实Bug的本意是“虫子”或者“昆虫”&#xff0c;在1947年9月9日&#xff0c;格蕾丝赫柏&#xff0c;一位为美国海军工作的电脑专家&#xff0c;也是最早…...

编程日记 2023/10/10 3:35:01

初识jmeter及简单使用

目录 1、打开页面&#xff1a; 2、添加线程组&#xff1a; 3、线程组中设置参数&#xff1a; 4、添加请求 5、添加一个http请求后&#xff0c;设置请求内容 6、添加察看结果树 7、执行&#xff0c;查看结果 一般步骤是&#xff1a;在测试计划下面新建一个线程组&#xf…...

编程日记 2023/10/10 3:34:01

Spring 在多线程环境下如何确保事务一致性

问题在现 如何解决异步执行 多线程环境下如何确保事务一致性 事务王国回顾 事务实现方式回顾 编程式事务 利用编程式事务解决问题 问题分析完了&#xff0c;那么如何解决问题呢&#xff1f; 小结 问题在现 我先把问题抛出来&#xff0c;大家就明白本文目的在于解决什…...

编程日记 2023/10/10 3:32:59

[Machine Learning] Learning with Noisy Data

文章目录 Probabilistic Perspective of NoiseBias and VarianceRobustness among Surrogate Loss FunctionsNMF Probabilistic Perspective of Noise 假设数据来源于一个确定的函数&#xff0c;叠加了高斯噪声。我们有&#xff1a; y h ( x ) ϵ y h(x) \epsilon yh(x)ϵ…...

编程日记 2023/10/10 3:31:56

C++中有哪些常用的标准库？

C中有许多常用的标准库&#xff0c;这些库提供了丰富的功能和工具&#xff0c;方便开发人员进行各种任务。以下是一些常见的C标准库&#xff1a; iostream&#xff1a;用于输入和输出操作&#xff0c;包括cin、cout和cerr等类和函数。algorithm&#xff1a;提供了许多常用的算…...

编程日记 2023/10/10 3:29:53