Deep learning of free boundary and Stefan problems论文阅读复现
Deep learning of free boundary and Stefan problems论文阅读复现
- 摘要
- 1. 一维一相Stefan问题
- 1.1 Direct Stefan problem
- 1.2 Inverse Type I
- 1.3 Inverse Type II
- 2. 一维二相Stefan问题
- 2.1 Direct Stefan problem
- 2.2 Inverse Type I
- 2.3 Inverse Type II
- 3. 二维一相Stefan问题
- 参考
摘要
在这项工作中,作者提出了一个基于物理信息神经网络的多网络模型,来解决一类一般的正和逆自由边界问题,称为Stefan问题。具体地说,用两个深度神经网络来近似未知解以及任何移动边界。作者提供了三个案例研究(一维一相Stefan问题,一维二相Stefan问题,二维一相Stefan问题),每个案例分别研究了正问题和两个逆问题,相关代码可以在https://github.com/PredictiveIntelligenceLab/DeepStefan获得。
复现代码环境:
conda create -n tensorflow1x python=3.6
conda activate tensorflow1x
pip install tensorflow==1.15.5 -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install pandas -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install seaborn -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install scipy -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple
1. 一维一相Stefan问题

- Direct Stefan problem: 已知 u 0 , g ( t ) , s 0 , h 1 ( t ) , h 2 ( t ) u_0, g(t), s_0, h_1(t), h_2(t) u0,g(t),s0,h1(t),h2(t) ,求解 u ( x , t ) : Ω → R . u(x,t):\Omega \rightarrow \mathbb{R}. u(x,t):Ω→R.
- Inverse Type I: 希望找到满足方程(3.1),(3.2),(3.5),(3.6)的温度分布 u ( x , t ) u(x,t) u(x,t) ,也希望当移动边界 s ( t ) s(t) s(t)已知时重构 Dirichlet 和 Neumann 边界条件。
- Inverse Type II: 给出域 Ω \Omega Ω 中的一些温度测量值,试图找到满足方程 (3.1),(3.4),(3.5) 的温度解 u ( x , t ) u(x,t) u(x,t),并确定移动边界 s(t) 的未知位置。

1.1 Direct Stefan problem
方程 (3.1)-(3.6) 中已知变量由 (3.7)-(3.8) 表示,(3.9) 和 (3.10) 分别是该问题的精确解和移动边界的解。
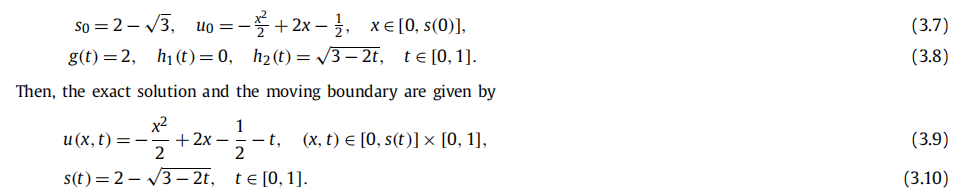
文章作者使用两个独立的神经网络近似潜在的 u ( x , t ) u(x,t) u(x,t) 和 s ( t ) s(t) s(t),训练40000epoch,一个epoch从初始条件 x = 0 , x=0, x=0, 边界条件 t = 0 , t=0, t=0, 和内部 Ω ∈ Ω ∗ = [ 0 , 1 ] × [ 0 , 1 ] \Omega \in \Omega^*=[0,1]\times[0,1] Ω∈Ω∗=[0,1]×[0,1] 中各随机选择一个batch_size(128)数据点进行训练,没有用到真解。由于 s ( t ) s(t) s(t) 在我们的问题设置中是未知的,所以我们不能简单地在 ( 0 , s ( t ) × ( 0 , t ) (0,s(t)\times(0,t) (0,s(t)×(0,t) 中进行采样点。处理这一技术问题的一种方法是对整个计算域 Ω ∗ \Omega^* Ω∗ 中的配置点进行采样,这是先验已知的,但然后通过将预测解 u θ ( x , t ) u_{\theta}(x,t) uθ(x,t) 限制在域 ( 0 , s β ( t ) × ( 0 , t ) (0,s_{\beta}(t)\times(0,t) (0,sβ(t)×(0,t) 来关注物理解。损失函数如下:
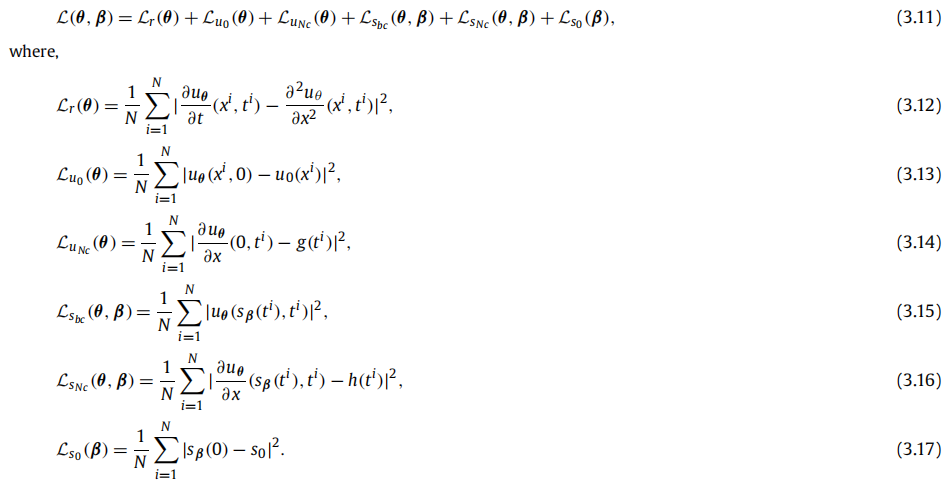
论文中实验结果:
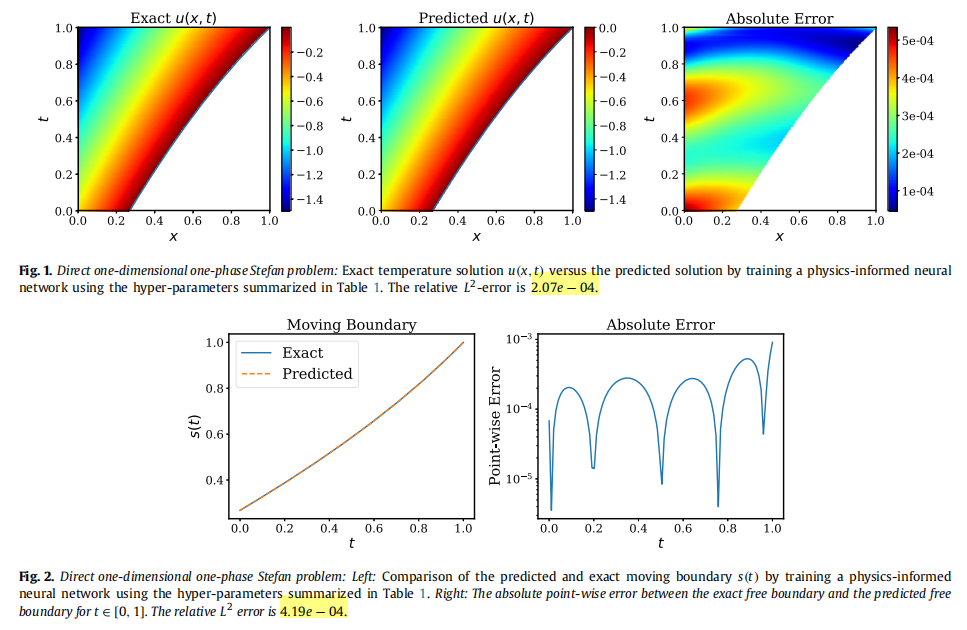
复现的实验结果:

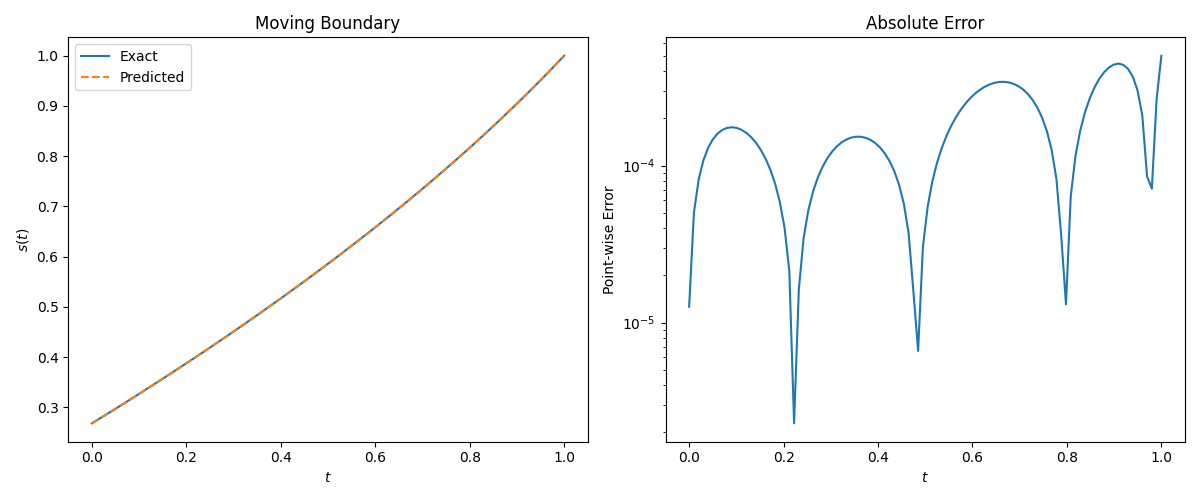
The u(x,t) relative L 2 L_2 L2-error is 4.64e-04.
The s(t) relative L 2 L_2 L2-error is 3.32e-04.
1.2 Inverse Type I
这种类型的逆问题也叫移动边界设计问题,这里的目标是找到满足方程 (3.1)-(3.6) 的解,并在给定自由边界 s ( t ) s(t) s(t) 信息的情况下恢复狄利克雷和诺伊曼边界条件 ( 3.18 ) (3.18) (3.18) 。

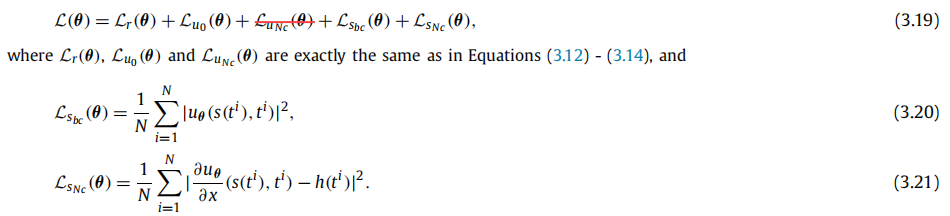
论文中实验结果:

复现实验结果:
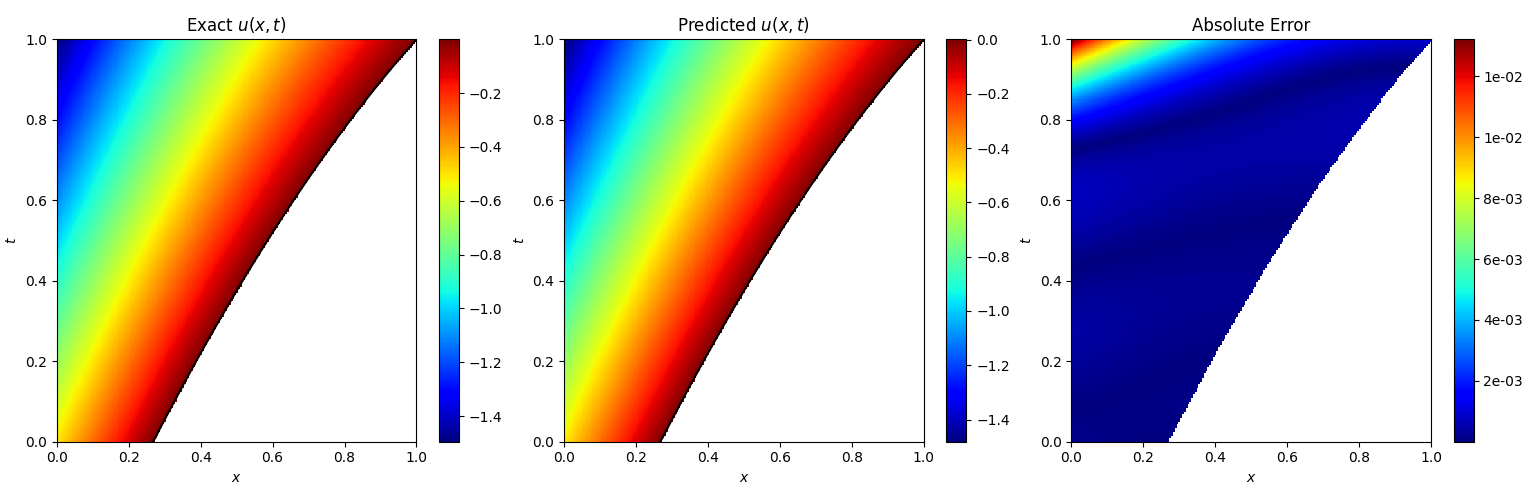
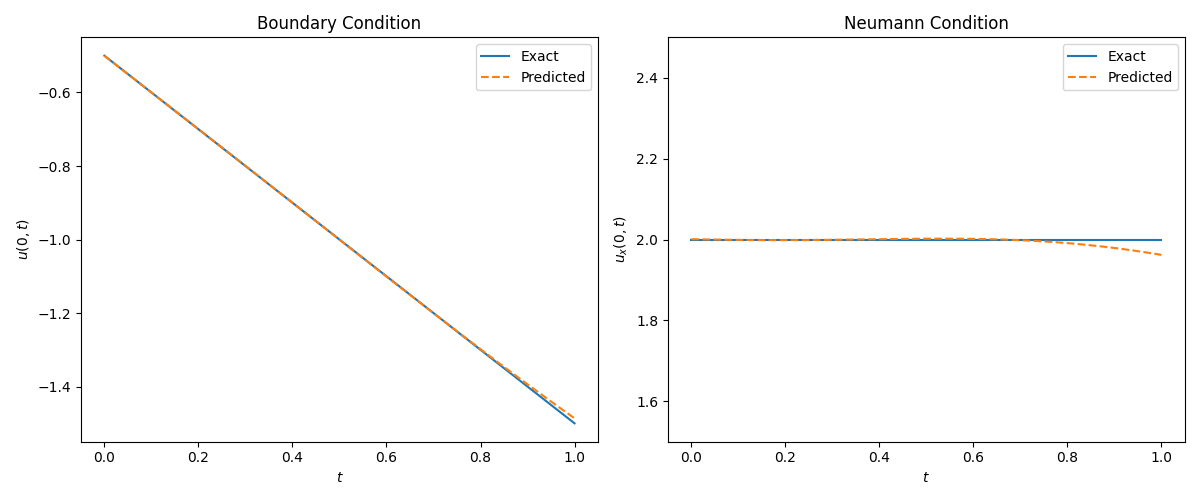
The u(x,t) relative L 2 L_2 L2-error is 2.48e-03.
The u θ u_{\theta} uθ(0,t) relative L 2 L_2 L2-error is 3.32e-03.
The ∂ u θ ∂ x \frac{\partial u_{\theta}}{\partial x} ∂x∂uθ(0,t) relative L 2 L_2 L2-error is 5.39e-03.
1.3 Inverse Type II
给定少量测试点 { u ( x d a t a j , t d a t a j ) } j = 1 M \{u(x_{data}^j, t_{data}^j)\}_{j=1}^M {u(xdataj,tdataj)}j=1M,我们想得到在域 Ω \Omega Ω 上符合热方程(3.1)的 u ( x , t ) u(x,t) u(x,t),以及未知边界符合(3.4)-(3.6)的 s ( t ) s(t) s(t),这样不需要任何初始或边界条件,这是接近许多现实的应用,这样的信息可能难以获得。为了解决这个问题,依然用两个神经网络 u θ ( x , t ) , s β ( t ) u_{\theta}(x,t),s_{\beta}(t) uθ(x,t),sβ(t) 近似 u ( x , t ) , s ( t ) u(x,t),s(t) u(x,t),s(t)。损失函数如下所示:
论文中实验结果:
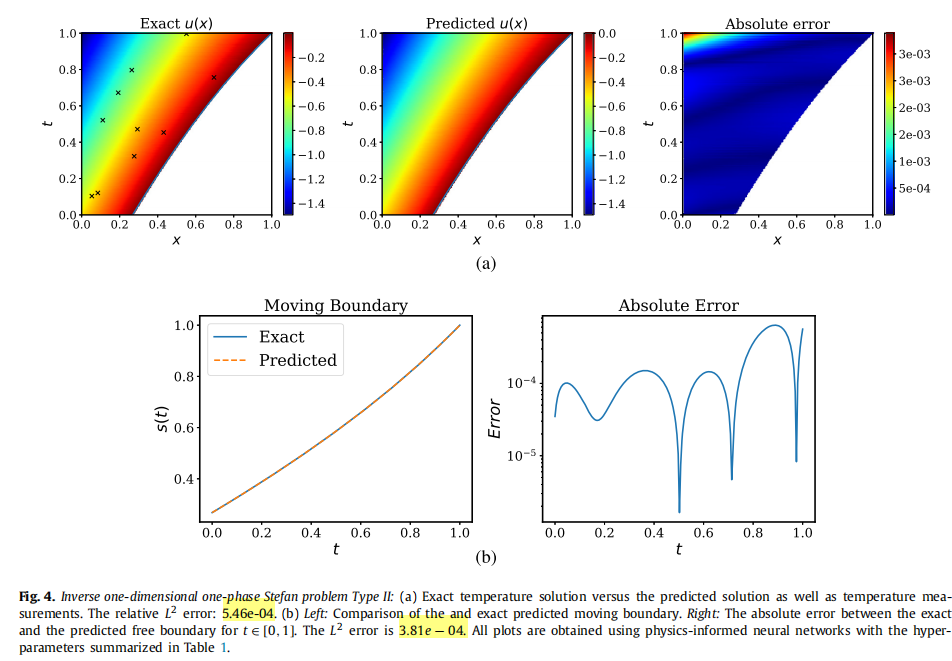
复现实验结果:
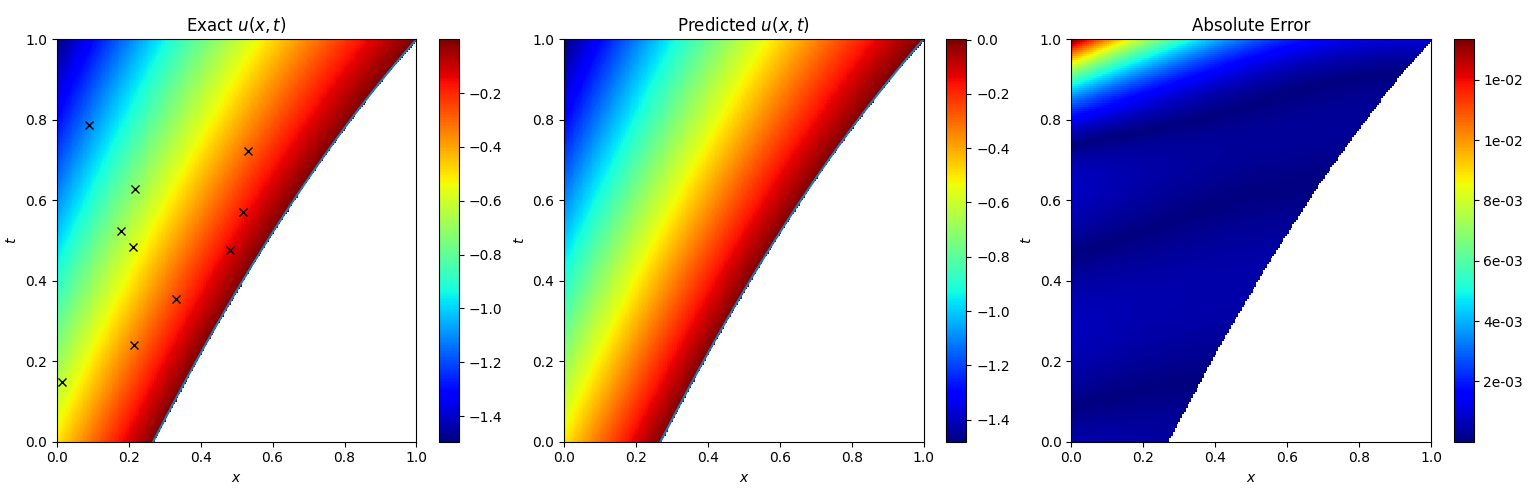
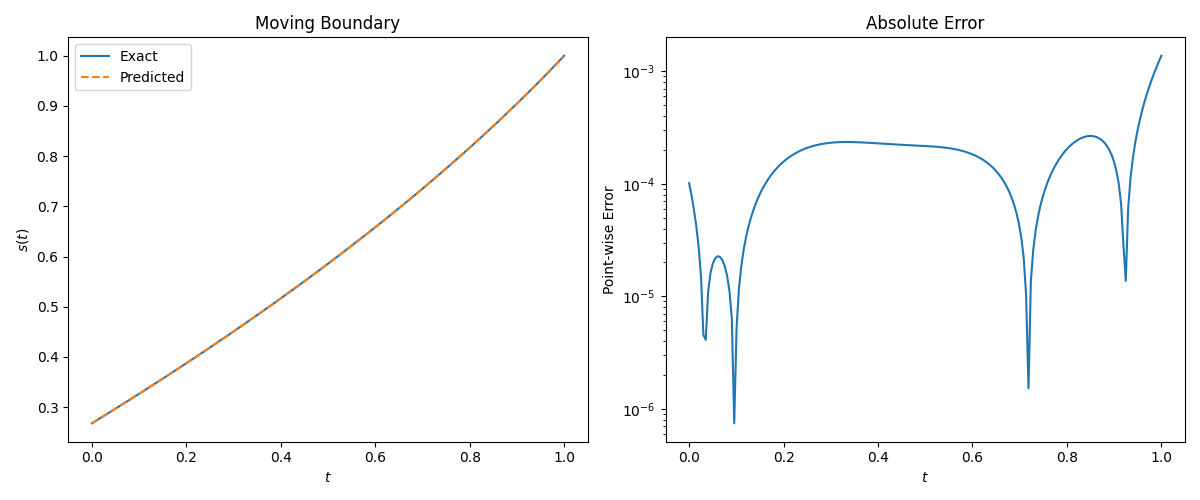
The u(x,t) relative L 2 L_2 L2-error is 2.83e-03.
The s(t) relative L 2 L_2 L2-error is 4.11e-04.
2. 一维二相Stefan问题
2.1 Direct Stefan problem
复现实验结果:
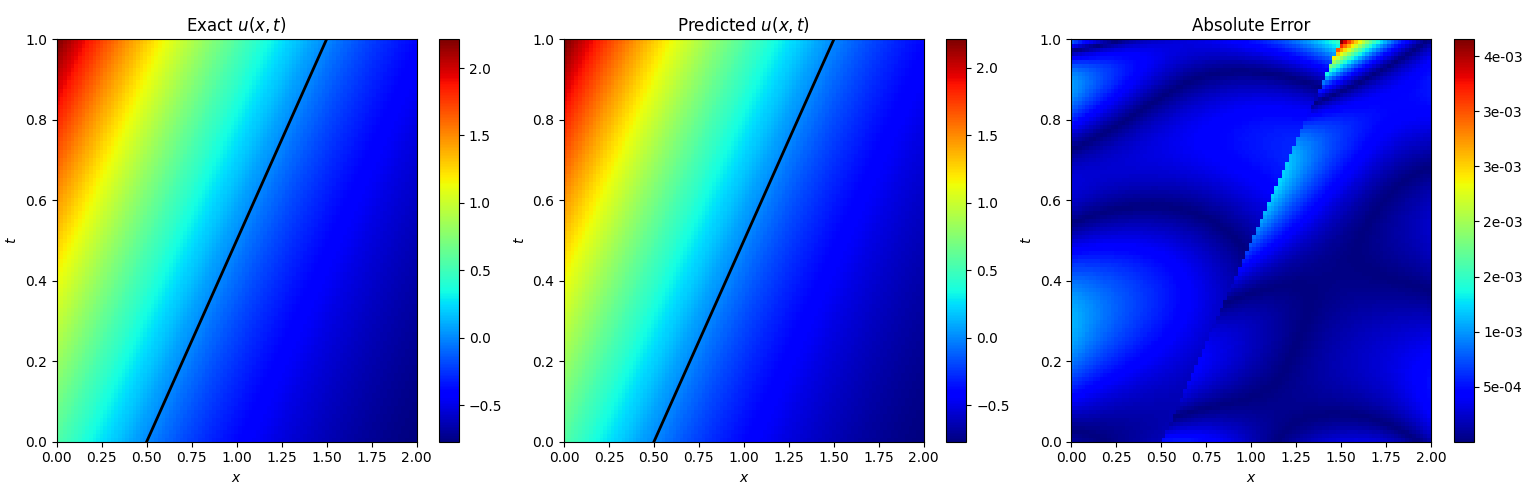
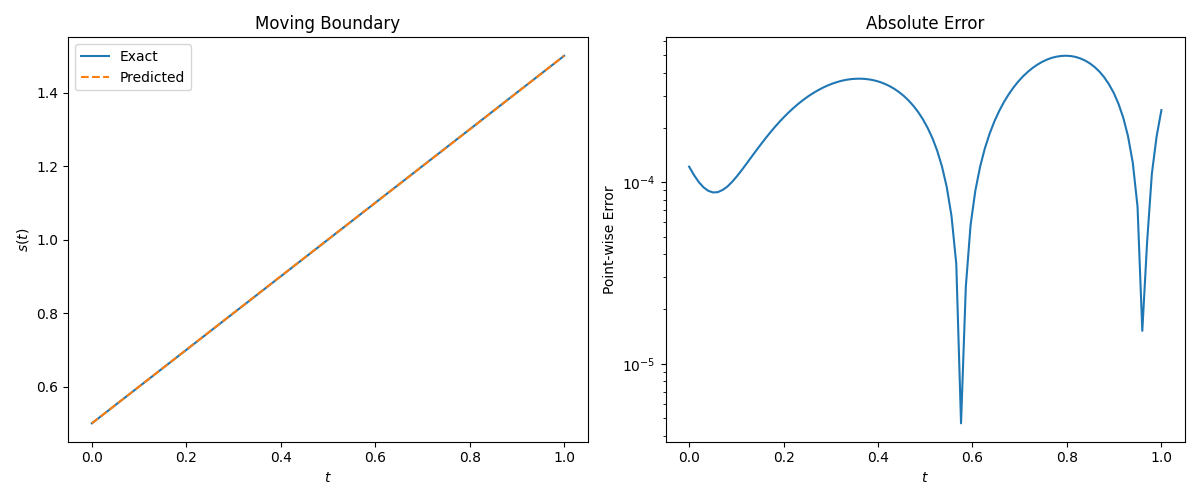
The u(x,t) relative L 2 L_2 L2-error is 6.35e-04.
The s(t) relative L 2 L_2 L2-error is 2.78e-04.
2.2 Inverse Type I
复现实验结果:
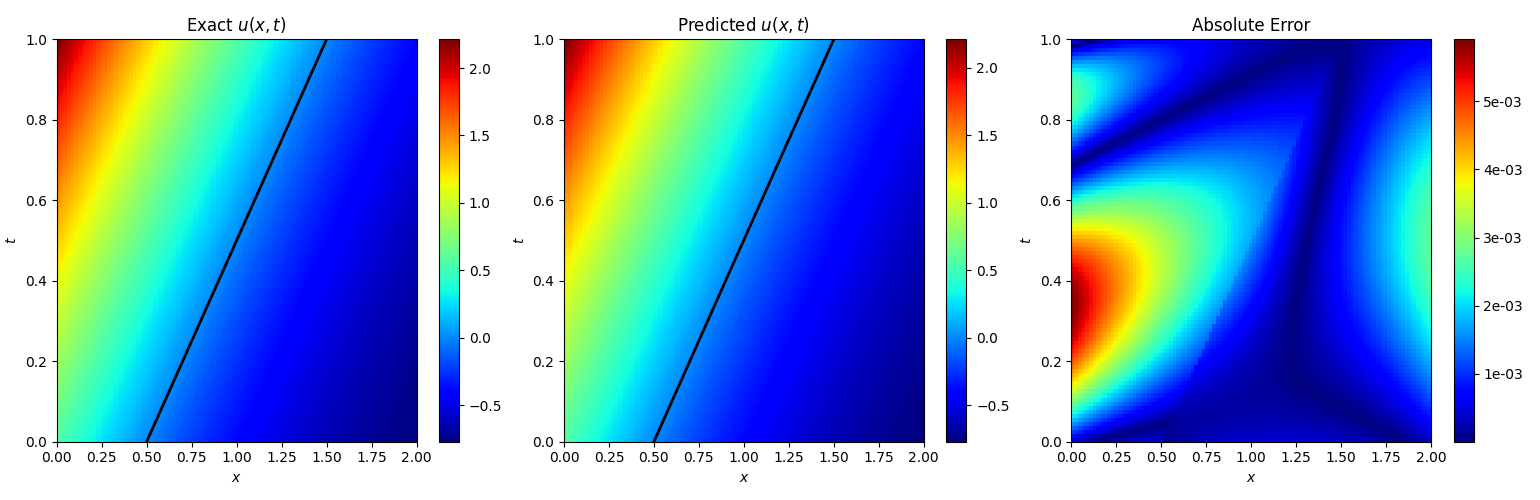
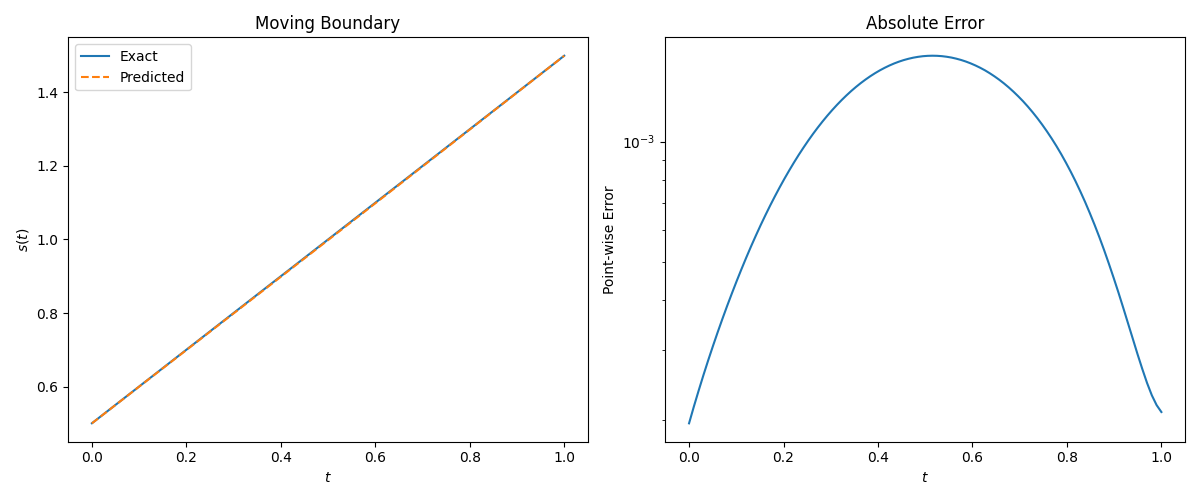
The u(x,t) relative L 2 L_2 L2-error is 2.71e-03.
The s(t) relative L 2 L_2 L2-error is 1.06e-03.
2.3 Inverse Type II
复现实验结果:
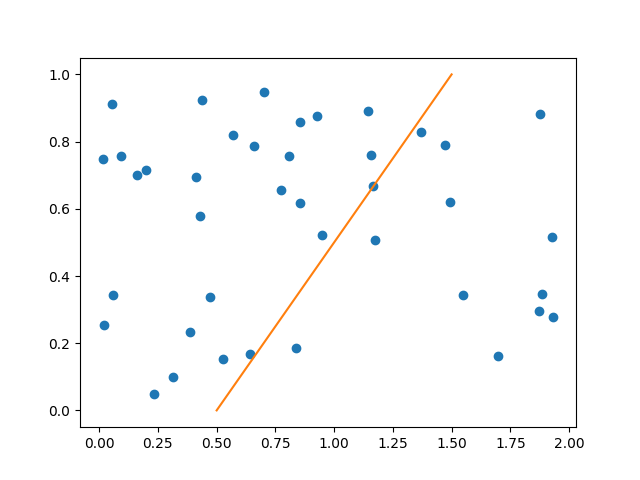
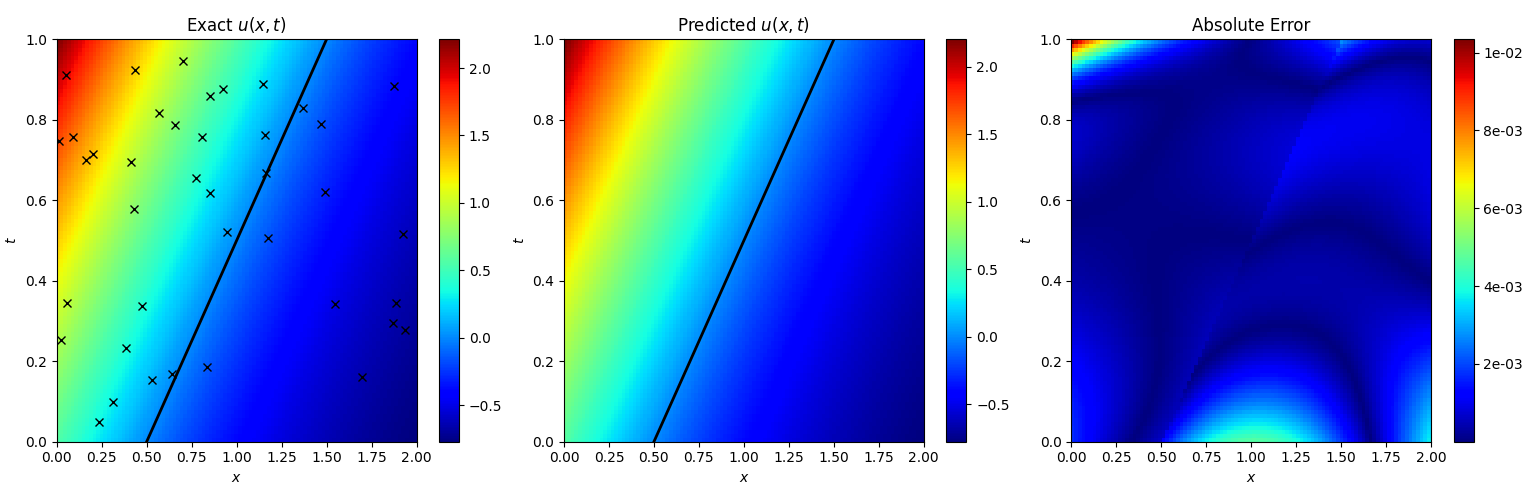
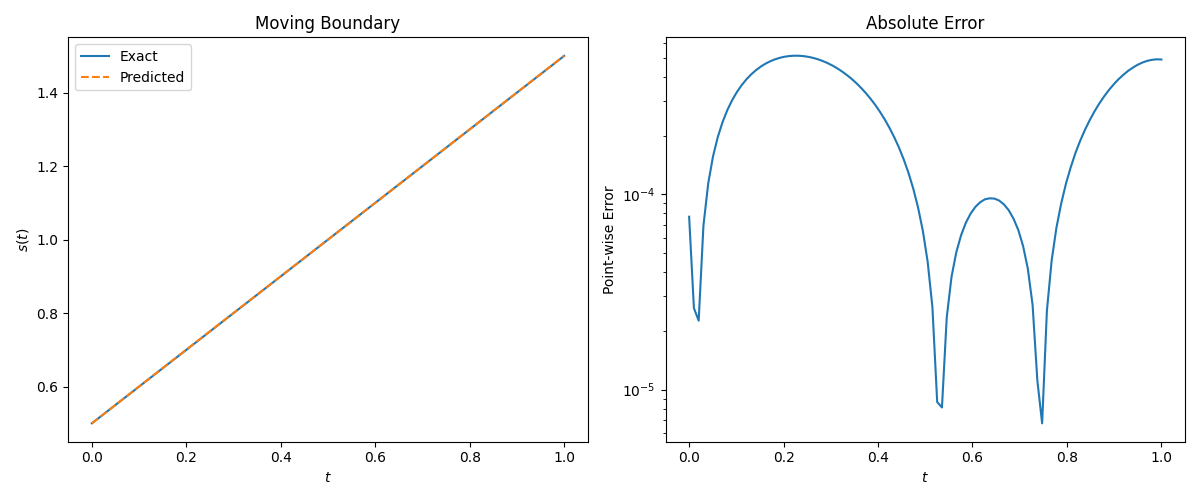
The u(x,t) relative L 2 L_2 L2-error is 1.71e-03.
The s(t) relative L 2 L_2 L2-error is 2.94e-04.
3. 二维一相Stefan问题
略
参考
[1] Deep learning of free boundary and Stefan problems
[2] https://github.com/PredictiveIntelligenceLab/DeepStefan
相关文章:

Deep learning of free boundary and Stefan problems论文阅读复现
Deep learning of free boundary and Stefan problems论文阅读复现 摘要1. 一维一相Stefan问题1.1 Direct Stefan problem1.2 Inverse Type I1.3 Inverse Type II 2. 一维二相Stefan问题2.1 Direct Stefan problem2.2 Inverse Type I2.3 Inverse Type II 3. 二维一相Stefan问题…...
LeetCode 1277. 统计全为 1 的正方形子矩阵【动态规划】1613
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

测试部门来了个00后卷王之王,老油条感叹真干不过,但是...
都说00后躺平了,但是有一说一,该卷的还是卷。 这不,前段时间我们公司来了个00后,工作都没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了…...

360 G800行车记录仪,不使用降压线如何开机,8芯插头的定义。
G800记录仪的插头是这样的,图中标出了线的颜色。其中红色为常电V,黑色为GND负极,黄色为ACC受车是否启动控制。 这个记录仪原装的电源线没有降压功能,所以这里的V是12V。 记录仪内部有电源板,负责将12V降压为5V。 如果…...
vue2踩坑之项目:Swiper轮播图使用
首先安装swiper插件 npm i swiper5 安装出现错误:npm ERR npm ERR! code ERESOLVE npm ERR! ERESOLVE could not resolve npm ERR! npm ERR! While resolving: vue/eslint-config-standard6.1.0 npm ERR! Found: eslint-plugin-vue8.7.1 npm ERR! node_modules/esl…...

python经典百题之分桃子
题目:海滩上有一堆桃子,五只猴子来分。第一只猴子把这堆桃子平均分为五份,多了一个,这只 猴子把多的一个扔入海中,拿走了一份。第二只猴子把剩下的桃子又平均分成五份,又多了 一个,它同样把多的一个扔入海中…...
vscode ssh linux C++ 程序调试
vscode调试c++程序相比vs2022要复杂很多,vs2022可以"一键运行调试",vscode则需要自己配置。 vscode调试程序时,会在当前工作目录产生.vscode 目录, 该目录有两个重要文件launch.json和tasks.json, 下面介绍两种调试方法: 手动调试和自动调试。 手动调试 不管…...

VUE和Angular有哪些区别?
Vue.js和Angular是两个流行的前端JavaScript框架,它们有一些明显的区别,包括以下几个方面: 1、语言和工具链的选择: Vue.js使用HTML、JavaScript和CSS来创建组件,使得它更容易学习,因为它使用了常见的Web…...
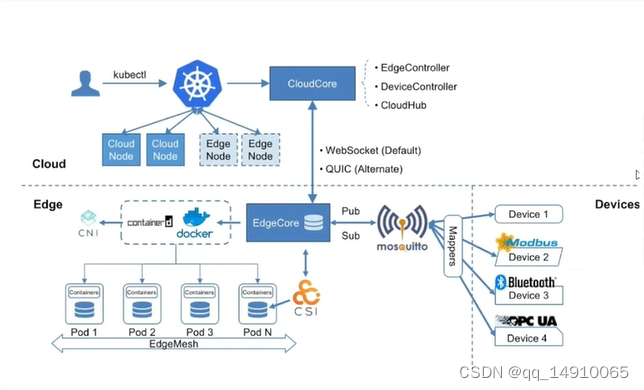
云原生边缘计算KubeEdge安装配置(二)
1. K8S集群部署,可以参考如下博客 请安装k8s集群,centos安装k8s集群 请安装k8s集群,ubuntu安装k8s集群 请安装kubeedge cloudcore centos安装K8S 2.安装kubEedge 2.1 编辑kube-proxy使用ipvs代理 kubectl edit configmaps kube-proxy -…...

SQL多表设计--一对多(外键)
-- 完成部门和员工的-- 选择当前db03 这个数据库use db03;-- 查看当前选中的数据库select database();-- 创建员工表create table tb_emp (id int unsigned primary key auto_increment comment ID,username varchar(20) not null unique comment 用户名,password varchar(32)…...
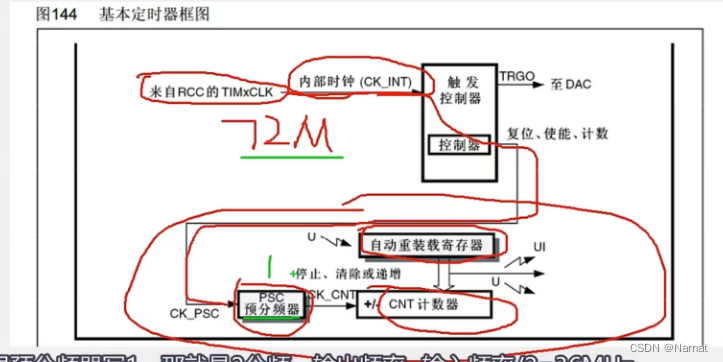
Stm32_标准库_9_TIM
频率(HZ)是频率的基本单位1HZ是1s的倒数 STM32F103C8T6一般情况给定时器的内部时钟都是72MHz(系统主频率) TIM基本构成 计数器、预分频器、自动化重装 // 都是16位其中计数器、自动化重装,都是16位换算成10进制范围为[0, 655536] 时间 1 /…...

283. 移动零
283. 移动零 原题 /** 左指针左边均为非零数; 右指针左边直到左指针处均为零。*/ class Solution {public void moveZeroes(int[] nums) {int left 0;int right 0;while(right<nums.length){if(nums[right]!0){swap(nums,left,right);left;}right;}}public v…...

用 HTTP 提交数据,基本就这 5 种方式
网页开发中,向服务端提交数据是一个基本功能,工作中会大量用 xhr/fetch 的 api 或者 axios 这种封装了一层的库来做。 可能大家都写过很多 http/https 相关的代码,但是又没有梳理下它们有哪几种呢? 其实通过 http/https 向服务端…...
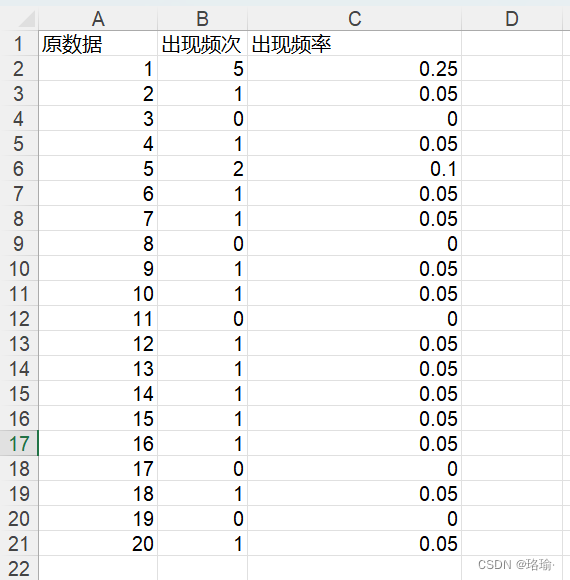
基于matlab统计Excel文件一列数据中每个数字出现的频次和频率
一、需求描述 如上表所示,在excel文件中,有一列数,统计出该列数中,每个数出现的次数和频率。最后,将统计结果输出到新的excel文件中。 二、程序讲解 第一步:选择excel文件; [Filename, Pathn…...
近期分享学习心得3
1、全屏组件封装 先看之前大屏端的监控部分全屏代码 整块全屏代码 常规流是下面这种 //进入全屏 function full(ele) {//if (ele.requestFullscreen) {// ele.requestFullscreen();//} else if (ele.mozRequestFullScreen) {// ele.mozRequestFullScreen();//} el…...
前端uniapp如何修改下拉框uni-data-select下面的uni-icons插件自带的图片【修改uniapp自带源码图片/图标】
目录 未改前图片未改前源码未改前通过top和bottom 和修改后图片转在线base64大功告成最后 未改前图片 未改前源码 然后注释掉插件带的代码,下面要的 未改前通过top和bottom 和修改后 找到uni-icons源码插件里面样式 图片转在线base64 地址 https://the-x.cn/b…...

【计算机基础】Git系列3:常用操作
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
有哪些值得推荐的Java 练手项目?
大家好,我是 jonssonyan 我是一名 Java 后端程序员,偶尔也会写一写前端,主要的技术栈是 JavaSpringBootMySQLRedisVue.js,基于我学过的技术认真的对每个分享的项目进行鉴别,今天就和大家分享我曾经用来学习的开源项目…...
节点)
【Godot】时间线(技能)节点
4.1 游戏中一般都会有各种各样的技能,或者其他需要按一定的时间顺序去执行的功能。 这里我写出了一个时间线节点,就像是在播放动画一样,按一定的阶段去执行某些功能 # # Timeline # # - author: zhangxuetu # - datetime: 2023-09-24 23…...

每日练习-9
目录 1、井字棋 2、密码强度等级 3、二维数组中的查找 4.调整数组奇数偶数 5.旋转数组中的最小元素 6、替换空格 1、井字棋 解析:井字棋有四种情况表示当前玩家获胜,行全为1, 列全为1,主对角全为1, 副对角全为1。遍历…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
