机器人中的数值优化(二十一)—— 伴随灵敏度分析、线性方程组求解器的分类和特点、优化软件
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
三十三、伴随灵敏度分析
伴随灵敏度分析可以避免冗余信息的计算,在下面的例子中,我们想要求解Ax=b1、Ax=b2 … Ax=bm等一系列方程组,第一种求解思路是将A矩阵进行LU分解, A = L U A=LU A=LU,求逆后可得到 A − 1 = U − 1 L − 1 A^{-1}=U^{-1}L^{-1} A−1=U−1L−1,然后依次将b1~bm代入下式即可得到这一系列方程组的解
x i = U − 1 L − 1 b i x_i=U^{-1}L^{-1}b_i xi=U−1L−1bi

但如果我们事先知道需要使用那些数据,那么我们能不能仅把需要使用的变量求出来?比如我们的目标是求每个xi的平均值ai,比如所有x1的平均值a1,那么我们是不是不需要求出每个xi的具体值,而仅仅需要他们的平均值ai。
a i = c T x i = c T A − 1 b i = b i T A − T c a_{i}=c^{T}x_{i}=c^{T}A^{-1}b_{i}=b_{i}^{T}A^{-T}c ai=cTxi=cTA−1bi=biTA−Tc
之前需要先算 A − 1 b i A^{-1}b_{i} A−1bi 部分,再算 c T A − 1 b i c^TA^{-1}b_i cTA−1bi,现在可以先算 A − T c A^{-T}c A−Tc,再算 b i T A − T c b_i^TA^{-T}c biTA−Tc,我们不需要对每个bi求一个线性方程组了,仅需要求一个方程组 q ≡ A − T c q\equiv A^{-T}c q≡A−Tc,求出 q q q之后,再与bi做一个点积即可, a i = b i T q a_i=b_i^Tq ai=biTq

伴随灵敏度分析的思想是在计算矩阵相乘的时候考虑那个先乘,那个后乘。线性方程组有一个伴随线性方程组,伴随灵敏度分析允许优化一小部分设计参数,而不是全部参数。
假设x是一个线性方程组的解,它的维度很大,它是一个完备的参数,从x可以获得所有我们想要的信息,但我们不能直接处理这么大维度的优化,我们需要设一组设计参数 p = ( p 1 , p 2 , . . . , p M ) \mathbf{p}=(p_{1},p_{2},...,p_{M}) p=(p1,p2,...,pM),我们要算的是一些目标函数 g ( p , x ) g(\mathbf{p},\mathbf{x}) g(p,x)关于参数 p 1 , p 2 , … , p M p_{1},p_{2},\ldots,p_{M} p1,p2,…,pM的梯度
d g d p j = ∂ g ∂ p j + ∑ i = 1 N ∂ g ∂ x i ∂ x i ∂ p j d g d p = g p + g x x p \begin{aligned}\frac{dg}{dp_j}&=\frac{\partial g}{\partial p_j}+\sum_{i=1}^N\frac{\partial g}{\partial x_i}\frac{\partial x_i}{\partial p_j}\\\\\frac{dg}{d\mathbf{p}}&=g_\mathbf{p}+g_\mathbf{x}\mathbf{x_p}\end{aligned} dpjdgdpdg=∂pj∂g+i=1∑N∂xi∂g∂pj∂xi=gp+gxxp

一般认为 ∂ g ∂ p j 和 ∂ g ∂ x i \frac{\partial g}{\partial p_j}和\frac{\partial g}{\partial x_i} ∂pj∂g和∂xi∂g是容易获得的, ∂ x i ∂ p j \frac{\partial x_{i}}{\partial p_{j}} ∂pj∂xi是不知道的
A p j x + A x p j = b p j ⇒ x p j = A − 1 [ b p j − A p j x ] A_{p_j}\mathbf{x}+A\mathbf{x}_{p_j}=b_{p_j}\quad\Rightarrow\quad\mathbf{x}_{p_j}=A^{-1}[b_{p_j}-A_{p_j}\mathbf{x}] Apjx+Axpj=bpj⇒xpj=A−1[bpj−Apjx]


我们使用矩阵相乘交换顺序的思想,把解m次 N 2 N^2 N2复杂度的方程组,转换为解一次就可以了

应用示例一:

应用示例二:
当路径上选取的优化点变密集后,安全性会更好,那么我们能不能,不选取那么多的优化点,而同样使其有较好的安全性

对于任意阶样条,我们可以解耦线段的数目和约束的数目。所有的路径点和持续时间都是我们轨迹的设计参数(决策变量)。样条系数是由路点确定的线性方程组的解。
A ( T ) c ( p , T ) = b ( p ) \mathbf{A(T)c(p,T)=b(p)} A(T)c(p,T)=b(p)
A和b构成了样条系数的线性方程组。这很自然地符合伴随敏感性分析的模型。

三十四、线性方程组求解器的分类和特点

线性方程组求解器可分为两大类或三小类,两大类即直接求解和迭代求解,直接求解可以得到Ax=b的精确解,迭代求解随着迭代次数的增多,所得到的近似解与精确解的误差也逐渐减小。三小类是因为有的求解器会利用矩阵的稀疏结构,而有的求解器不利用,因此,直接法又分为稠密法和稀疏直接法。
(1)稠密法
具有简单数据结构,不需要索引数据结构等特殊的数据结构,采用矩阵的直接表示,主要是O(N3)分解算法
(2)稀疏直接法
当矩阵中有很多0元素时,我们可以仅储存非0元素的位置和具体的值,使其占较少的内存。
因子分解成本取决于问题结构(1D低成本;2D可接受成本;3D高成本;不容易给出一般规则,NP难以排序以获得最佳稀疏性)
(3)迭代法
迭代求取近似解,仅需要知道 y = A x ( m a y b e y = A T x ) y=Ax\mathrm{~(maybe~}y=A^Tx) y=Ax (maybe y=ATx),良好的收敛性取决于预条件。

–
当我们求解Ax=b时,如果是稠密的矩阵,尽可能的根据矩阵的对称性、半正定性、带状结构等特点,以此来挑选不同的稠密求解器,比如使用LAPACK/ScaLAPACK库,或者Eigen库

若,我们知道矩阵的非零元素比零元素少很多,可以选用稀疏直接法中的求解器,看看能不能提前把矩阵预分解

如果问题比较大,如 1 0 5 10^5 105,此时采用稠密法会有问题,可以用CG方法处理正定对称矩阵,还有一系列迭代法可以处理对称不定或非对称的矩阵。

因式分解有很多种方法,比如
L U , L L T / L L H , L D L T / L D L H , Q R , L Q , Q R Z , generalized QR and RQ \begin{aligned}LU,LL^T /LL^H,LDL^T/LDL^H,QR,LQ,QRZ,\end{aligned}\text{generalized QR and RQ} LU,LLT/LLH,LDLT/LDLH,QR,LQ,QRZ,generalized QR and RQ
除了因式分解,还有对称/Hermitian和非对称特征值、奇异值分解、广义特征值与奇异值分解

LU分解其实就是高斯消元法,把一个矩阵进行高斯消元,进行一些行变换
A = P L U A=PLU A=PLU

稀疏LU分解法不仅需要做行变换,还需要做列变换。

Cholesky分解:

稀疏Cholesky分解:

LDL分解:

稀疏矩阵:


稀疏矩阵分解:

稀疏排序会对虚实化的稀疏性产生巨大的影响:

选择产生最小二乘分解的排序的一般问题是困难的,但是,几个简单的启发式方法是非常有效的。例如嵌套排序方法,可以起作用。


迭代法:

三十五、优化软件
1、swMATH
里面包含优化、线性代数、大规模矩阵运算等丰富的资源
链接:https://zbmath.org/software/

2、gamsworld
gamsworld收录了很多的工具,在这里可以找到锥规划等性能测评的手段
链接:https://gamsworld.org/
链接:https://github.com/GAMS-dev/gamsworld

3、DECISION TREE FOR OPTIMIZATION SOFTWARE
可以根据优化问题的结构,查找某个问题有哪些现有的方案
链接:http://plato.asu.edu/guide.html

4、Mathematical Software
里面包含优化、非线性求解器等丰富的资源
链接:https://arnold-neumaier.at/software.html

5、neos solvers
neos solvers是比较有名的求解器
链接:https://neos-server.org/neos/solvers/index.html

6、netlib
里面几乎包含所有的线性求解办法
链接:https://netlib.org/

7、GAMS
里面包含一些数学库,不仅仅是优化
链接:https://gams.nist.gov/

8、HSL Software
专门的线性方程组求解器,包含很多源代码
链接:https://www.hsl.rl.ac.uk/catalogue/

9、autodiff
收集了一些求微分的方法的网站
链接:https://www.autodiff.org/

10、Local Optimization Software
链接:https://arnold-neumaier.at/glopt/software_l.html

11、Global Optimization Software
链接:https://arnold-neumaier.at/glopt/software_g.html

参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化
相关文章:

机器人中的数值优化(二十一)—— 伴随灵敏度分析、线性方程组求解器的分类和特点、优化软件
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

BACnet /IP转MQTT网关
在工业自动化和楼宇自动化领域中,Modbus、MQTT和BACnet/IP是三种常用的通信协议。Modbus是一种串行通信协议,常用于连接工业电子设备;MQTT是一种基于发布/订阅模式的轻量级通信协议,适用于远程监测和控制系统;BACnet/I…...
Web API 基础 (Web Workers API)
Web Workers API 1、指南 1.1 使用Web Workers Web Workers是一种让Web内容在后台线程中运行脚本的简单方法。工作线程可以在不干扰用户界面的情况下执行任务。此外,它们还可以使用XMLHttpRequest(尽管responseXML和channel属性总是为空)或fetch(没有此类限制)执…...

如何看待程序员不写注释?
程序员对代码注释可以说是又爱又恨又双标……你是怎么看待程序员不写注释这一事件的呢? 对于程序员来说,注释是一种非常重要的实践,可以帮助他们自己和其他人更好地理解和维护代码。以下是一些关于注释的观点: 维护代码的重要性&a…...

2.6 方法
思维导图: 2.6.1 什么是方法 ### 2.6.1 什么是方法 **定义**: - 方法就是一段可以重复调用的代码,使得程序的可读性、可维护性都得以提高。 **示例**: - 假设有一个游戏中需要反复发射炮弹。而发射炮弹的代码有100行。为了避免在程序中多次写下这100…...
【排序算法】插入排序
文章目录 一:基本概念1.1 介绍1.2 原理1.3 插入排序法思想 二:代码实现2.1 源码2.2 执行结果2.3 测试八万条数据 三:算法分析3.1 时间复杂度3.2 空间复杂度3.3 稳定性 一:基本概念 1.1 介绍 插入式排序属于内部排序法࿰…...

Gnuradio+AM解调
1. https://wiki.gnuradio.org/index.php/PLL_Carrier_Tracking 2. https://wiki.gnuradio.org/index.php?titleComplex_to_Mag#Example_Flowgraph...

解决java.io.IOException: Broken pipe的报错
问题说明: 订单服务,查询预售但是出现Broken pipe; 测试版是正常的,正式版报错 解决方案 1、延长客户端超时时间 // 查询预售单列表 export function listPreOrder(query) {return request({url: /order/presale/list,method:…...

微信小程序--》从模块小程序项目案例23.10.09
配置导航栏 导航栏是小程序的门户,用户进来第一眼看到的便是导航栏,其起着对当前小程序主题的概括。而我们 新建的小程序 时,第一步变开始配置导航栏。如下: 配置tabBar 因为配置tabBar需要借助字体图标,我这里平常喜…...

爱尔眼科角膜塑形镜验配超百万,全力做好“角塑镜把关人”
你知道吗?过去的2022年,我国儿童青少年总体近视率为53.6%,其中6岁儿童为14.5%,小学生为36%,初中生为71.6%,高中生为81%①。儿童青少年眼健康问题俨然成为全社会关心的热点与痛点,牵动着每一个人的神经。 好…...

机器学习DAYX:线性回归与逻辑回归
线性回归 多重线性回归 逻辑回归...

【网络安全】网络安全的最后一道防线——“密码”
网络安全的最后一道防线——“密码” 前言超星学习通泄露1.7亿条信息事件武汉市地震监测中心遭境外网络攻击事件 一、密码起源1、 古代密码2、近代密码3、现代密码4、量子密码 二、商密专栏推荐三、如何利用密码保护账号安全?1、账号安全的三大危险?&…...
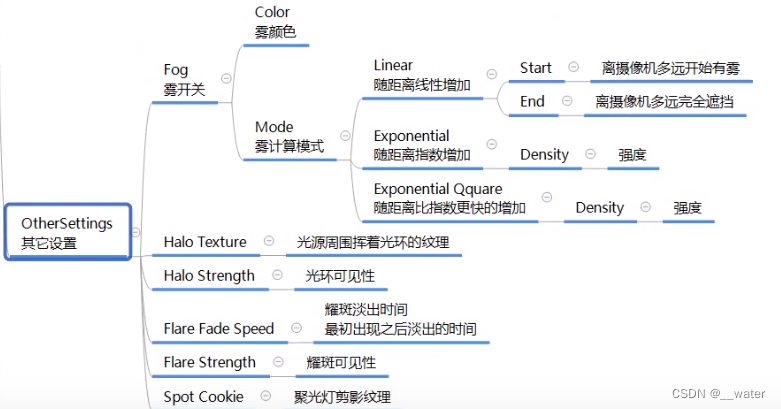
unity操作_光源组件 c#
准备工作 添加资源导入后先不管,现在主要学习自带Directional Light 我们首先创建一个平面Plane 然后重置一下位置 然后创建一个Cube 也重置一下位置然后修改y0.5刚好在这个平面上 ctrl d复制一个Cube 修改位置和旋转角度 给物体一个颜色 接下来创建一个点光源 我们…...

2023年全球市场氮化铝外延片总体规模、主要生产商、主要地区、产品和应用细分研究报告
按收入计,2022年全球氮化铝外延片收入大约9百万美元,预计2029年达到25百万美元,2023至2029期间,年复合增长率CAGR为 16.1%。同时2022年全球氮化铝外延片销量大约 ,预计2029年将达到 。2022年中国市场规模大约为 百万美…...

C++特性:继承,封装,多态
继承 封装 类把⾃⼰的数据和⽅法只让可信的类或者对象操作,对不可信的进⾏隐藏,如:将公共的数据或⽅法使⽤public修饰,⽽不希望被访问的数据或⽅法采⽤private修饰 多态 即向不同对象发送同⼀消息,不同的对象在接收…...

交通物流模型 | 基于双向时空自适应Transformer的城市交通流预测
城市交通流预测是智能交通系统的基石。现有方法侧重于时空依赖建模,而忽略了交通预测问题的两个内在特性。首先,不同预测任务的复杂性在不同的空间(如郊区与市中心)和时间(如高峰时段与非高峰时段)上分布不均匀。其次,对过去交通状况的回忆有利于对未来交通状况的预测。基于…...

【香橙派-OpenCV-Torch-dlib】TF损坏变成RAW格式解决方案及python环境配置
前言 本文将介绍在香橙派(Orange Pi)开发板上进行软件配置和环境搭建的详细步骤,以便运行Python应用程序。这涵盖了以下主要内容: 获取所需软件:提供了香橙派操作系统和balenaEtcher工具的下载链接,以确保…...

HDMI协议介绍(五)--Audio
基础知识 I2S(inter-IC sound bus)飞利浦公司制定的标准,既规定了硬件接口规范,也规定了数字音频数据格式。 硬件接口规范 I2S接口有3个主要信号: 时钟信号 Serial Clock 串行时钟SCK,也叫位时钟(BCLK)&…...
Centos7中安装Jenkins教程
1.必须先配置jdk环境,安装jdk参考 Linux配置jdk 2.先卸载Jenkins # rpm卸载 rpm -e jenkins # 检查是否卸载成功 rpm -ql jenkins # 彻底删除残留文件 find / -iname jenkins | xargs -n 1000 rm -rf 3.安装Jenkins 在 /usr/ 目录下创建 jenkins文件夹 mkdir -p je…...

十一、WSGI与Web框架
目录 一、什么是WSGI1.1 WSGI接口的组成部分1.2 关于environ 二、简易的web框架实现2.1 文件结构2.2 在web/my_web.py定义动态响应内容2.3 在html/index.html中定义静态页面内容2.4 在web_server.py中实现web服务器框架2.5 测试 三、让简易的web框架动态请求支持多页面3.1 修改…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
