【排序算法】插入排序
文章目录
- 一:基本概念
- 1.1 介绍
- 1.2 原理
- 1.3 插入排序法思想
- 二:代码实现
- 2.1 源码
- 2.2 执行结果
- 2.3 测试八万条数据
- 三:算法分析
- 3.1 时间复杂度
- 3.2 空间复杂度
- 3.3 稳定性
一:基本概念
1.1 介绍
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
1.2 原理
一般也被称为 直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排席方法,它的基本思想是
将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增 1 的有序表。在其实现过程使用双层循环,外层循环对除
了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
1.3 插入排序法思想
插入排序(InsertionSorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
- 将待排序序列分为两部分,一部分有序一部分无序。
- 我们把第一个元素看作有序序列,从第二个元素到最后为无序序列。
- 将无序序列中每一个元素依次插入到有序序列的合适位置–从小到大(从大到小)。

二:代码实现
2.1 源码
/*** 插入排序** @author ikun*/
public class InsertSort {public static void main(String[] args) {int[] array = new int[5];for (int i = 0; i < array.length; i++) {//Math.random() * 80000生成0到100的随机数array[i] = (int) (Math.random() * 80);}System.out.println("排序前:" + Arrays.toString(array));insertSort(array);}/*** 插入排序** @param array 需要排序的数组*/public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {//使用逐步推倒的方式来讲解,便于理解//第一轮 {101, 34, 119, 1} -> { 34,101,119,1}//定义待插入的数据//第一轮的话,待插入的数就是array[1]int insertVal = array[i];//定义待插入数据的下标,即array[1]的前一个下标//int insertIndex = 1 - 1;int insertIndex = i - 1;//给insertVal找到一个插入的位置//说明//1.insertIndex >= 0是保证再给insertIndex找插入位置时,不会数组下标越界//2.insertVal < array[insertIndex]说明待插入的数,还没找到插入的位置//3.此时需要将array[insertIndex],也就是101后移while (insertIndex >= 0 && insertVal < array[insertIndex]) {//将array[insertIndex]后移array[insertIndex + 1] = array[insertIndex];//因为要和前面每一个数据进行比较,所以要将要插入的位置减一,挨个比较insertIndex--;}//当退出while循环时,说明插入的位置找到,则insertIndex + 1array[insertIndex + 1] = insertVal;System.out.println("第" + i + "轮插入后:" + Arrays.toString(array));}}}
2.2 执行结果
2.3 测试八万条数据
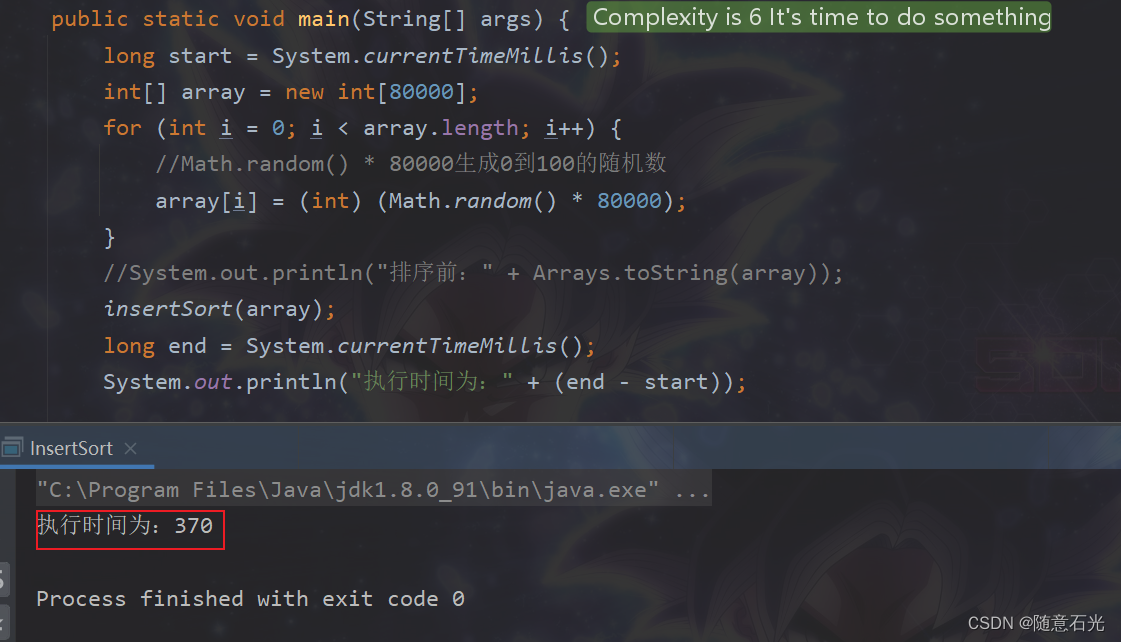
可以看出执行的时间只有370ms,是低于冒泡排序和选择排序的
三:算法分析
3.1 时间复杂度
O(n2)
3.2 空间复杂度
O(1)
3.3 稳定性
稳定的排序算法,其稳定性在于相同值的元素进行插入排序完成后相对位置不发生改变。
相关文章:

【排序算法】插入排序
文章目录 一:基本概念1.1 介绍1.2 原理1.3 插入排序法思想 二:代码实现2.1 源码2.2 执行结果2.3 测试八万条数据 三:算法分析3.1 时间复杂度3.2 空间复杂度3.3 稳定性 一:基本概念 1.1 介绍 插入式排序属于内部排序法࿰…...

Gnuradio+AM解调
1. https://wiki.gnuradio.org/index.php/PLL_Carrier_Tracking 2. https://wiki.gnuradio.org/index.php?titleComplex_to_Mag#Example_Flowgraph...

解决java.io.IOException: Broken pipe的报错
问题说明: 订单服务,查询预售但是出现Broken pipe; 测试版是正常的,正式版报错 解决方案 1、延长客户端超时时间 // 查询预售单列表 export function listPreOrder(query) {return request({url: /order/presale/list,method:…...

微信小程序--》从模块小程序项目案例23.10.09
配置导航栏 导航栏是小程序的门户,用户进来第一眼看到的便是导航栏,其起着对当前小程序主题的概括。而我们 新建的小程序 时,第一步变开始配置导航栏。如下: 配置tabBar 因为配置tabBar需要借助字体图标,我这里平常喜…...

爱尔眼科角膜塑形镜验配超百万,全力做好“角塑镜把关人”
你知道吗?过去的2022年,我国儿童青少年总体近视率为53.6%,其中6岁儿童为14.5%,小学生为36%,初中生为71.6%,高中生为81%①。儿童青少年眼健康问题俨然成为全社会关心的热点与痛点,牵动着每一个人的神经。 好…...

机器学习DAYX:线性回归与逻辑回归
线性回归 多重线性回归 逻辑回归...

【网络安全】网络安全的最后一道防线——“密码”
网络安全的最后一道防线——“密码” 前言超星学习通泄露1.7亿条信息事件武汉市地震监测中心遭境外网络攻击事件 一、密码起源1、 古代密码2、近代密码3、现代密码4、量子密码 二、商密专栏推荐三、如何利用密码保护账号安全?1、账号安全的三大危险?&…...
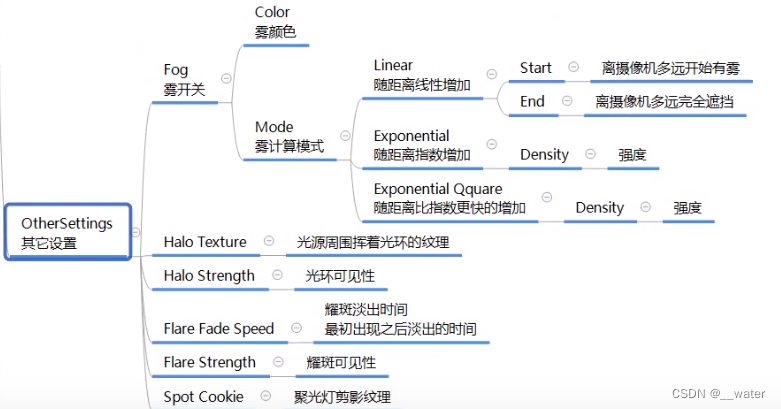
unity操作_光源组件 c#
准备工作 添加资源导入后先不管,现在主要学习自带Directional Light 我们首先创建一个平面Plane 然后重置一下位置 然后创建一个Cube 也重置一下位置然后修改y0.5刚好在这个平面上 ctrl d复制一个Cube 修改位置和旋转角度 给物体一个颜色 接下来创建一个点光源 我们…...

2023年全球市场氮化铝外延片总体规模、主要生产商、主要地区、产品和应用细分研究报告
按收入计,2022年全球氮化铝外延片收入大约9百万美元,预计2029年达到25百万美元,2023至2029期间,年复合增长率CAGR为 16.1%。同时2022年全球氮化铝外延片销量大约 ,预计2029年将达到 。2022年中国市场规模大约为 百万美…...

C++特性:继承,封装,多态
继承 封装 类把⾃⼰的数据和⽅法只让可信的类或者对象操作,对不可信的进⾏隐藏,如:将公共的数据或⽅法使⽤public修饰,⽽不希望被访问的数据或⽅法采⽤private修饰 多态 即向不同对象发送同⼀消息,不同的对象在接收…...

交通物流模型 | 基于双向时空自适应Transformer的城市交通流预测
城市交通流预测是智能交通系统的基石。现有方法侧重于时空依赖建模,而忽略了交通预测问题的两个内在特性。首先,不同预测任务的复杂性在不同的空间(如郊区与市中心)和时间(如高峰时段与非高峰时段)上分布不均匀。其次,对过去交通状况的回忆有利于对未来交通状况的预测。基于…...

【香橙派-OpenCV-Torch-dlib】TF损坏变成RAW格式解决方案及python环境配置
前言 本文将介绍在香橙派(Orange Pi)开发板上进行软件配置和环境搭建的详细步骤,以便运行Python应用程序。这涵盖了以下主要内容: 获取所需软件:提供了香橙派操作系统和balenaEtcher工具的下载链接,以确保…...

HDMI协议介绍(五)--Audio
基础知识 I2S(inter-IC sound bus)飞利浦公司制定的标准,既规定了硬件接口规范,也规定了数字音频数据格式。 硬件接口规范 I2S接口有3个主要信号: 时钟信号 Serial Clock 串行时钟SCK,也叫位时钟(BCLK)&…...
Centos7中安装Jenkins教程
1.必须先配置jdk环境,安装jdk参考 Linux配置jdk 2.先卸载Jenkins # rpm卸载 rpm -e jenkins # 检查是否卸载成功 rpm -ql jenkins # 彻底删除残留文件 find / -iname jenkins | xargs -n 1000 rm -rf 3.安装Jenkins 在 /usr/ 目录下创建 jenkins文件夹 mkdir -p je…...

十一、WSGI与Web框架
目录 一、什么是WSGI1.1 WSGI接口的组成部分1.2 关于environ 二、简易的web框架实现2.1 文件结构2.2 在web/my_web.py定义动态响应内容2.3 在html/index.html中定义静态页面内容2.4 在web_server.py中实现web服务器框架2.5 测试 三、让简易的web框架动态请求支持多页面3.1 修改…...

[idekCTF 2022]Paywall - LFI+伪协议+filter_chain
[idekCTF 2022]Paywall 一、解题流程(一)、分析(二)、解题 二、思考总结 一、解题流程 (一)、分析 点击source可以看到源码,其中关键部分:if (isset($_GET[p])) {$article_content…...
Python 自动化Web测试
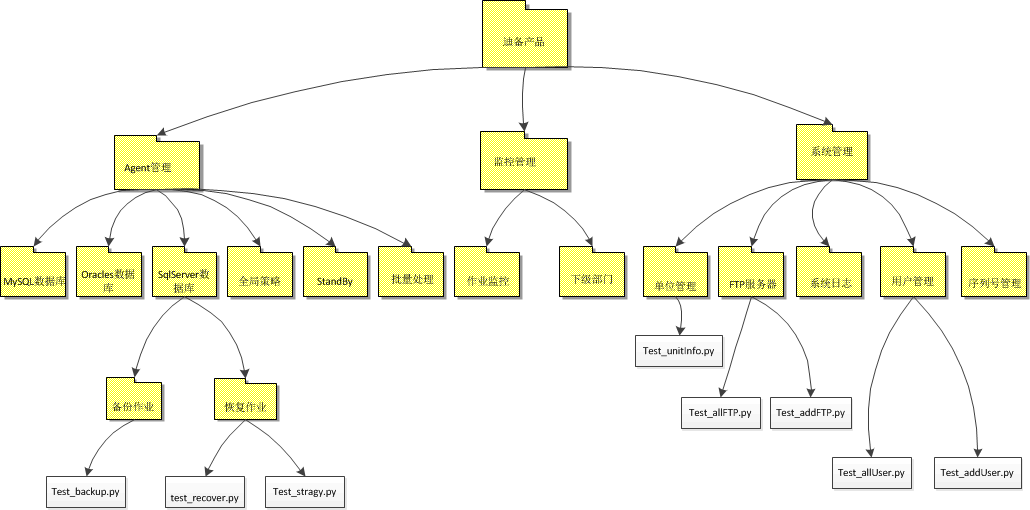
限于作者水平有限,以下内容可能是管窥之见,希望大家高抬贵手,且让我斗胆抛砖引玉。 公司产品迪备主要是通过网页操作来进行数据库的备份与恢复,监控与管理,因此在测试的过程中,可以用python测试脚本来模拟…...
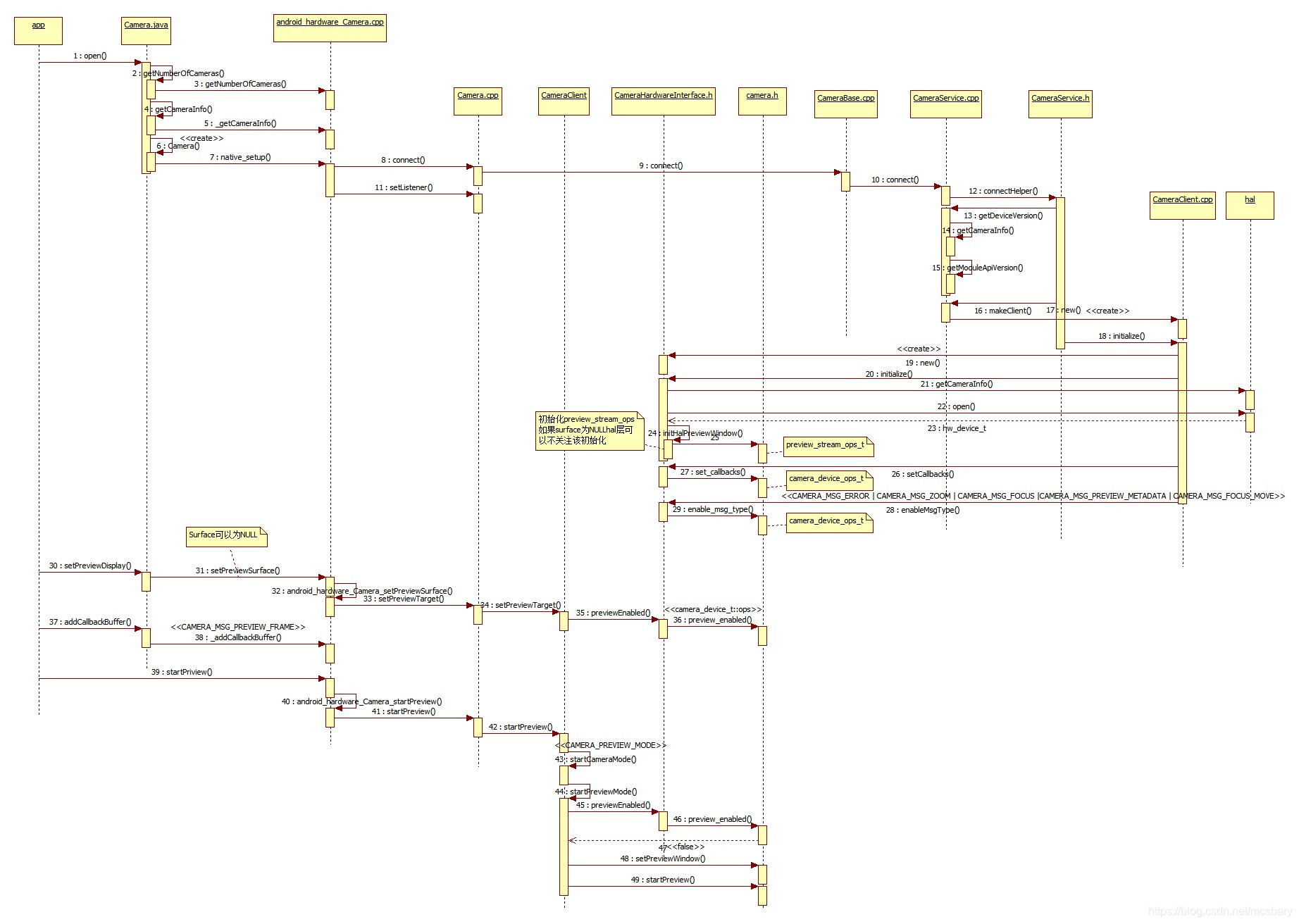
MM-Camera架构-Preview 流程分析
目录 文章目录 1 log开的好,问题都能搞2 lib3 preview3.1 打开视频流3.1.1 cpp\_module\_start\_session3.1.2 cpp\_thread\_create3.1.3 cpp\_thread\_funcsundp-3.1 cpp\_hardware\_open\_subdev(ctrl->cpphw)sundp-3.2 cpp\_hardware\_process\_command(ctrl-…...

科普文章|一文了解平行链及其优势
平行链是一种可以连接到更大规模的区块链网络(波卡)的独立区块链。不同于传统区块链(如比特币和以太坊)是孤立的并且无法在本地相互通信,平行链与其他平行链并行运行,并且相互可以无缝通信。平行链还使用波…...
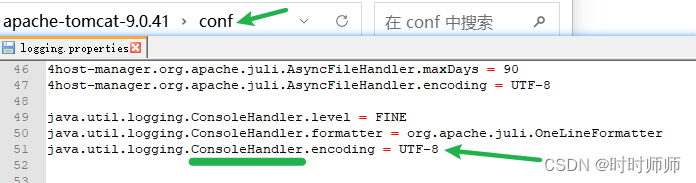
Tomcat 9.0.41在IDEA中乱码问题(IntelliJ IDEA 2022.1.3版本)
1. 乱码的产生是由于编码和解码的编码表不一致引起的。 2. 排查乱码原因 2.1 在idea中启动Tomcat时控制台乱码排查 Tomcat输出日志乱码: 首先查看IDEA控制台,检查发现默认编码是GBK。 再查看Tomcat日志(conf文件下logging.properties)的默…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
