Java数据结构之Deque(双端队列)
一、Queue和Deque异同介绍
我们知道,Queue是队列,只能一头进,另一头出。
如果把条件放松一下,允许两头都进,两头都出,这种队列叫双端队列(Double Ended Queue),学名Deque。
Java集合提供了接口Deque来实现一个双端队列,它的功能是:
既可以添加到队尾,也可以添加到队首;
既可以从队首获取,又可以从队尾获取。
首先我们比较下Queue和Deque出队和入队的方法:
| Queue | Deque | |
| 添加元素到队尾 | add(E e) / offer(E e) | addLast(E e) / offerLast(E e) |
| 取队首元素并删除 | E remove() / E poll() | E removeFirst() / E pollFirst() |
| 取队首元素但不删除 | E element() / E peek() | E getFirst() / E peekFirst() |
| 添加元素到队首 | 无 | addFirst(E e) / offerFirst(E e) |
| 取队尾元素并删除 | 无 | E removeLast() / E pollLast() |
| 取队尾元素但不删除 | 无 | E getLast() / E peekLast() |
注:这里解释先为什么Queue或者Deque都有两种方法,它们有什么区别?
1、add()和offer()区别:
add()和offer()都是向队列中添加一个元素。一些队列有大小限制,因此如果想在一个满的队列中加入一个新项,调用 add() 方法就会抛出一个 unchecked 异常,而调用 offer() 方法会返回 false。因此就可以在程序中进行有效的判断!
2、poll()和remove()区别:
remove() 和 poll() 方法都是从队列中删除第一个元素。如果队列元素为空,调用remove() 的行为与 Collection 接口的版本相似会抛出异常,但是新的 poll() 方法在用空集合调用时只是返回 null。因此新的方法更适合容易出现异常条件的情况。
3、element() 和 peek()区别:
element() 和 peek() 用于在队列的头部查询元素。与 remove() 方法类似,在队列为空时, element() 抛出一个异常,而 peek() 返回 null。
上面介绍的是Queue的两中方法,Deque也是相同的就不介绍了。
二、Deque作为队列和堆栈的介绍
我们知道Queue的数据结构是一个队列,即:FIFO(先进先出)。从队尾添加元素,从对头删除元素。Deque也有等效的方法作为一个FIFO队列,具体方法如下:
Queue 方法 | 等效 Deque 方法 |
|---|---|
| add(e) | addLast(e) |
| offer(e) | offerLast(e) |
| remove() | removeFirst() |
| poll() | pollFirst() |
| element() | getFirst() |
| peek() | peekFirst() |
Deque(双端队列)也可以用作LIFO(后进先出)堆栈(也就是栈),应优先使用此接口而不是遗留 Stack类。在将双端队列用作堆栈时,元素被推入双端队列的开头并从双端队列开头弹出。堆栈方法完全等效于Deque 方法,如下表所示:
| 堆栈方法 | 等效 Deque 方法 |
|---|---|
| push(e) | addFirst(e) |
| pop() | removeFirst() |
| peek() | peekFirst() |
总结:
1、Queue只能从队尾插入,从对头删除。
2、Deque对头队尾都可以进行插入和删除。
3、Deque根据不同的插入和删除方法可以实现队列和堆栈(也就是栈)这两种数据结构。
相关文章:
)
Java数据结构之Deque(双端队列)
一、Queue和Deque异同介绍 我们知道,Queue是队列,只能一头进,另一头出。 如果把条件放松一下,允许两头都进,两头都出,这种队列叫双端队列(Double Ended Queue),学名Deq…...

flink以增量+全量的方式更新广播状态
背景 flink在实现本地内存和db同步配置表信息时,想要做到类似于增量(保证实时性) 全量(保证和DB数据一致)的效果,那么我们如何通过flink的广播状态外部定时器定时全量同步的方式来实现呢? 实现增量全量的效果 package wikiedits.schedule…...

Java:org.apache.commons.io包的工具类:IOUtils、FileUtils、FilenameUtils
文档 https://commons.apache.org/proper/commons-io/https://central.sonatype.com/artifact/commons-io/commons-io/2.14.0/jar 工具类 IOUtils io工具类FileUtils 文件操作工具类FilenameUtils 文件名工具类 依赖 <dependency><groupId>commons-io</gro…...
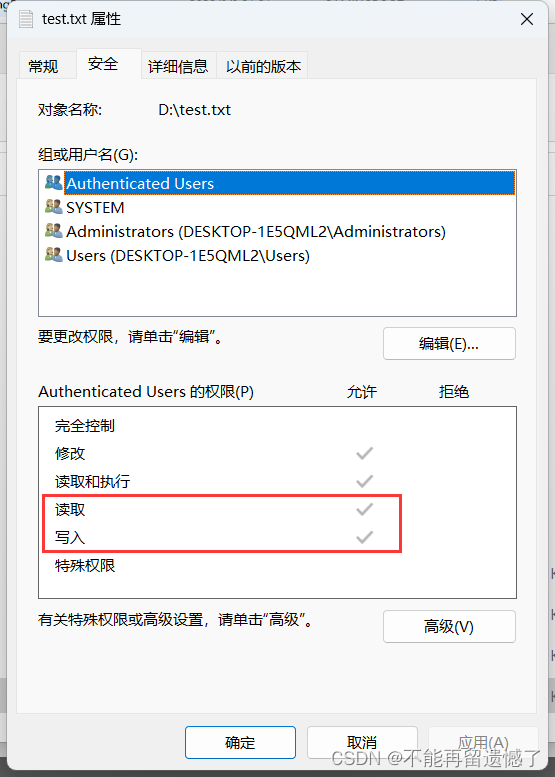
【JavaEE】文件操作
文章目录 前言什么是文件树型结构组织和目录文件路径文件类型文件权限Java中的文件操作File 类的常见属性File 类常见构造方法File 类常用方法 前言 文件是我们日常生活中使用非常广泛的,我们使用任何一个程序都离不开文件操作,这个文件不仅仅指平时可以…...
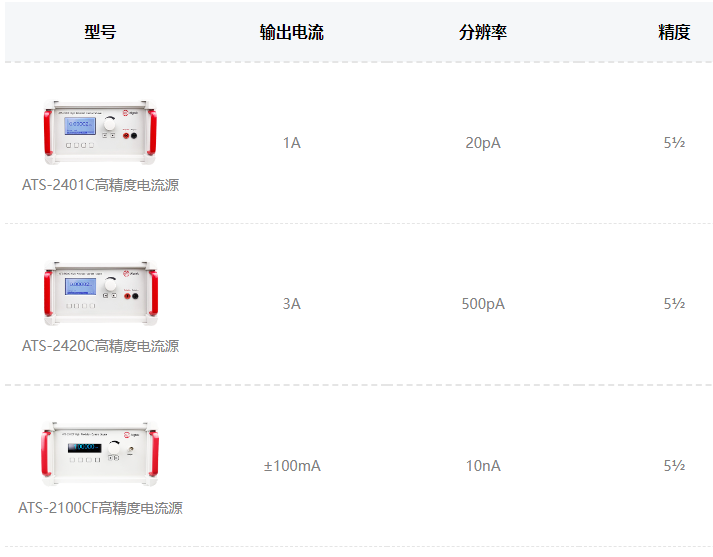
高精度电流源的应用领域有哪些
高精度电流源是一种能够提供稳定、准确、可控的电流输出的仪器设备,广泛应用于多个领域。以下是一些高精度电流源的应用领域。 科学研究:在物理学、化学、材料科学等领域中,需要进行精确的电流实验和测试。高精度电流源可以提供稳定的电流输出…...

多线程 - 线程池
线程池 相关的背景知识 线程池存在的意义: 使用进程来实现并发编程,效率太低了,任务太重了,为了提高效率,此时就引入了线程,线程也叫做“轻量级进程”,创建线程比创建进程更高效;销毁线程比销毁进程更高效;调度线程比调度进程更高效…此时,使用多线程就可以在很多时候代替进程…...

vue3 setup中defineEmits与defineProps的使用案例
目录 一、defineEmits的使用 二、 defineProps的使用 总结 一、defineEmits的使用 使用说明 1、在子组件中调用defineEmits并定义要发射给父组件的方法 const emits defineEmits([foldChange]) 2、使用defineEmits会返回一个方法,使用一个变量emits(变量名随意…...
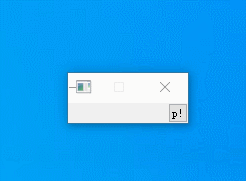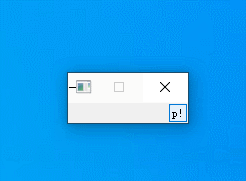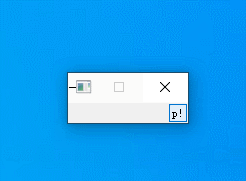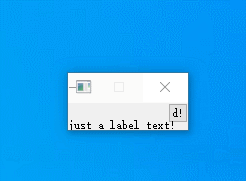
Vs - Qt - 下拉窗口示例
下列代码定义了一个窗口,窗口采用竖直布局:一个按钮及一个label。按下按钮时候,窗口扩张,显示label控件。再次按下按钮时,窗口收缩,隐藏label控件。 详细代码如下: #include <QApplication&g…...

深圳自贸区的形成与发展
深圳自贸区的形成与发展源于中国政府推出的自贸试验区政策。自贸试验区是指在特定区域内,允许实行特殊的行政管理措施和贸易政策,以促进贸易自由化、投资便利化和经济转型升级。 深圳自贸区成立于2015年4月以来,主要着眼于优化区域布局、提高…...

机器人中的数值优化(二十一)—— 伴随灵敏度分析、线性方程组求解器的分类和特点、优化软件
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

BACnet /IP转MQTT网关
在工业自动化和楼宇自动化领域中,Modbus、MQTT和BACnet/IP是三种常用的通信协议。Modbus是一种串行通信协议,常用于连接工业电子设备;MQTT是一种基于发布/订阅模式的轻量级通信协议,适用于远程监测和控制系统;BACnet/I…...
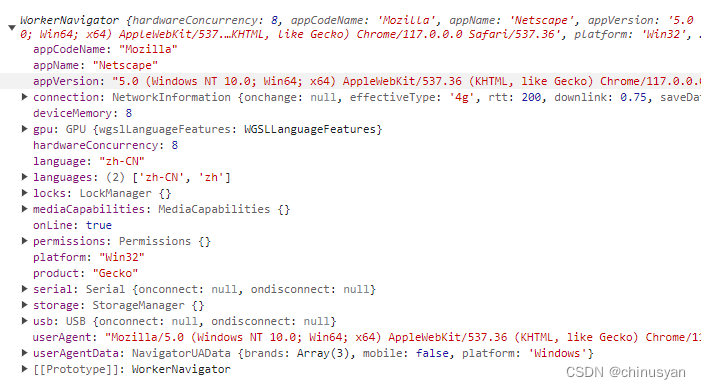
Web API 基础 (Web Workers API)
Web Workers API 1、指南 1.1 使用Web Workers Web Workers是一种让Web内容在后台线程中运行脚本的简单方法。工作线程可以在不干扰用户界面的情况下执行任务。此外,它们还可以使用XMLHttpRequest(尽管responseXML和channel属性总是为空)或fetch(没有此类限制)执…...

如何看待程序员不写注释?
程序员对代码注释可以说是又爱又恨又双标……你是怎么看待程序员不写注释这一事件的呢? 对于程序员来说,注释是一种非常重要的实践,可以帮助他们自己和其他人更好地理解和维护代码。以下是一些关于注释的观点: 维护代码的重要性&a…...

2.6 方法
思维导图: 2.6.1 什么是方法 ### 2.6.1 什么是方法 **定义**: - 方法就是一段可以重复调用的代码,使得程序的可读性、可维护性都得以提高。 **示例**: - 假设有一个游戏中需要反复发射炮弹。而发射炮弹的代码有100行。为了避免在程序中多次写下这100…...
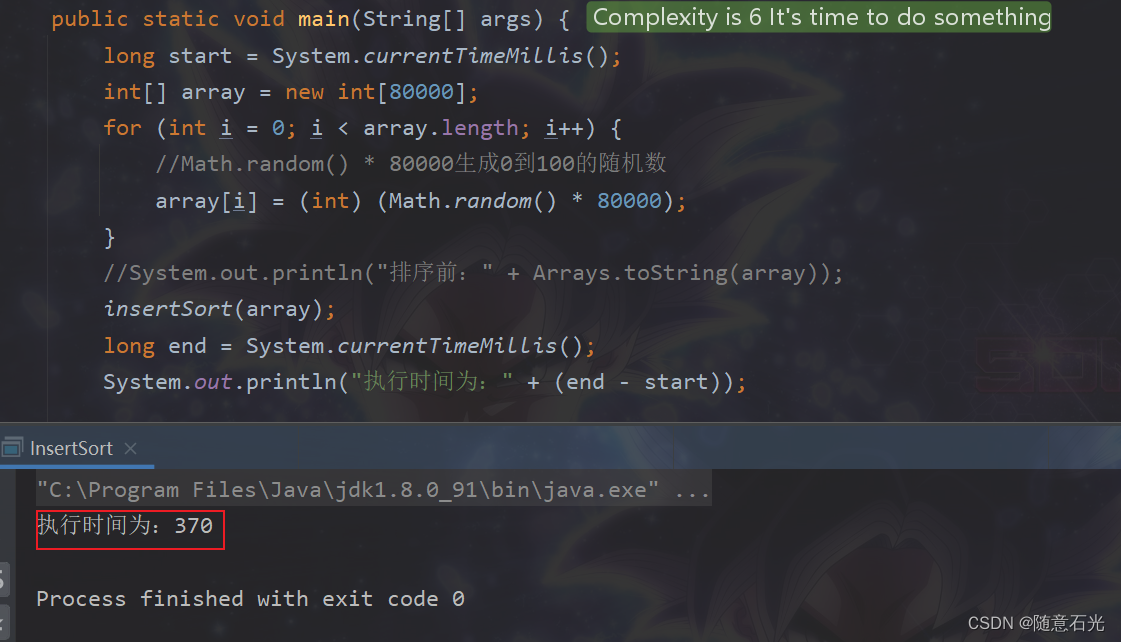
【排序算法】插入排序
文章目录 一:基本概念1.1 介绍1.2 原理1.3 插入排序法思想 二:代码实现2.1 源码2.2 执行结果2.3 测试八万条数据 三:算法分析3.1 时间复杂度3.2 空间复杂度3.3 稳定性 一:基本概念 1.1 介绍 插入式排序属于内部排序法࿰…...

Gnuradio+AM解调
1. https://wiki.gnuradio.org/index.php/PLL_Carrier_Tracking 2. https://wiki.gnuradio.org/index.php?titleComplex_to_Mag#Example_Flowgraph...

解决java.io.IOException: Broken pipe的报错
问题说明: 订单服务,查询预售但是出现Broken pipe; 测试版是正常的,正式版报错 解决方案 1、延长客户端超时时间 // 查询预售单列表 export function listPreOrder(query) {return request({url: /order/presale/list,method:…...

微信小程序--》从模块小程序项目案例23.10.09
配置导航栏 导航栏是小程序的门户,用户进来第一眼看到的便是导航栏,其起着对当前小程序主题的概括。而我们 新建的小程序 时,第一步变开始配置导航栏。如下: 配置tabBar 因为配置tabBar需要借助字体图标,我这里平常喜…...

爱尔眼科角膜塑形镜验配超百万,全力做好“角塑镜把关人”
你知道吗?过去的2022年,我国儿童青少年总体近视率为53.6%,其中6岁儿童为14.5%,小学生为36%,初中生为71.6%,高中生为81%①。儿童青少年眼健康问题俨然成为全社会关心的热点与痛点,牵动着每一个人的神经。 好…...

机器学习DAYX:线性回归与逻辑回归
线性回归 多重线性回归 逻辑回归...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
