深度学习笔记之优化算法(六)RMSprop算法的简单认识
深度学习笔记之优化算法——RMSProp算法的简单认识
- 引言
- 回顾:AdaGrad算法
- AdaGrad算法与动量法的优化方式区别
- AdaGrad算法的缺陷
- RMProp算法
- 关于AdaGrad问题的优化方式
- RMSProp的算法过程描述
- RMSProp示例代码
引言
上一节对 AdaGrad \text{AdaGrad} AdaGrad算法进行了简单认识,本节将介绍 RMSProp \text{RMSProp} RMSProp方法。
回顾:AdaGrad算法
AdaGrad算法与动量法的优化方式区别
与动量法、 Nesterov \text{Nesterov} Nesterov动量法在迭代过程中对梯度方向进行优化不同, AdaGrad \text{AdaGrad} AdaGrad算法在迭代过程中对梯度大小(学习率)进行优化,两者优化的思路本质上存在区别。其迭代过程对比表示如下:
关于动量法在计算当前迭代步骤的梯度m t m_t mt时,使用了m t − 1 , ∇ θ ; t − 1 J ( θ t − 1 ) m_{t-1},\nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) mt−1,∇θ;t−1J(θt−1)加权和(向量加法)的方式来优化m t m_t mt的方向;当方向固定后,在判断沿着 m t m_t mt方向前进的步长时,仅使用了固定的学习率η \eta η作为前进步长。而AdaGrad \text{AdaGrad} AdaGrad算法对当前时刻的梯度信息G t \mathcal G_t Gt并没有执行任何方向上的优化;在判断步长时使用η R t + ϵ ⇒ η \begin{aligned}\frac{\eta}{\sqrt{\mathcal R_t} + \epsilon} \Rightarrow \eta\end{aligned} Rt+ϵη⇒η执行更新操作,其本质上是向量与标量之间的乘法操作。
Momentum : { m t = β ⋅ m t − 1 + ( 1 − β ) ⋅ ∇ θ ; t − 1 J ( θ t − 1 ) θ t = θ t − 1 − η ⋅ m t AdaGrad : { G t = ∇ θ ; t − 1 J ( θ t − 1 ) R t = R t − 1 + G t ⊙ G t θ t = θ t − 1 − η R t + ϵ ⊙ G t \begin{aligned} & \text{Momentum : } \begin{cases} m_t = \beta \cdot m_{t-1} + (1 - \beta) \cdot \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \theta_t = \theta_{t-1} - \eta \cdot m_t \end{cases} \\ & \text{AdaGrad : } \quad \begin{cases} \mathcal G_t = \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \mathcal R_t = \mathcal R_{t-1} + \mathcal G_t \odot \mathcal G_t \\ \begin{aligned} \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\mathcal R_t} + \epsilon} \odot \mathcal G_t \end{aligned} \end{cases} \end{aligned} Momentum : {mt=β⋅mt−1+(1−β)⋅∇θ;t−1J(θt−1)θt=θt−1−η⋅mtAdaGrad : ⎩ ⎨ ⎧Gt=∇θ;t−1J(θt−1)Rt=Rt−1+Gt⊙Gtθt=θt−1−Rt+ϵη⊙Gt
AdaGrad算法的缺陷
引入上一节使用 AdaGrad \text{AdaGrad} AdaGrad算法对目标函数 f ( x ) = x T Q x ; x = ( x 1 , x 2 ) T ; Q = ( 0.5 0 0 20 ) f(x) = x^T \mathcal Q x;x = (x_1,x_2)^T;\mathcal Q = \begin{pmatrix}0.5 \quad 0 \\ 0 \quad 20\end{pmatrix} f(x)=xTQx;x=(x1,x2)T;Q=(0.50020)的迭代过程:
我们能够观察到:虽然该算法在梯度较小的、平缓的倾斜方向能够稳定的前进,但是同样也会观察到:在迭代算法的中后段,算法消耗了相当多的迭代步骤,原因也很明显:此时的学习率 η \eta η太小了,并且还会无限的小下去。
上述示例中的目标函数是一个强凸函数,它存在全局最优解;因此迭代的最终结果也只会趋近最优解;但如果目标函数是一个复杂函数呢 ? ? ?就像这样:
画的不太好,凑合着看~

观察上图,黄色点描述的是使用 AdaGrad \text{AdaGrad} AdaGrad算法,权重在不同迭代步骤下的更新位置;如果该目标函数是一个简单的凸函数,它可能最终会收敛至某一点,例如红色点;但如果该函数比较复杂,在本段迭代过程之后,梯度又重新增加(图中最左侧黄点位置)那么此时的收敛速度又是什么样的呢 ? ? ?
上一节提到过: AdaGrade \text{AdaGrade} AdaGrade的学习率只会减小,不会增加,即便后续的梯度又重新增大,但它的学习率不会增加,只会更加缓慢地继续更新。
对应《深度学习(花书)》P188 8.5.1中的原文:从训练开始时累积梯度平方会导致有效学习率过早地、过量地减小。
之所以 AdaGrad \text{AdaGrad} AdaGrad算法的学习率只减不增,究其原因还是:在累积平方梯度的过程中,平方梯度 G t ⊙ G t \mathcal G_t \odot \mathcal G_t Gt⊙Gt被完整地保存在累积梯度变量 R \mathcal R R中。这种现象在 Nesterov \text{Nesterov} Nesterov动量法中也提到过:在迭代步骤较深时,初始迭代步骤的历史平方梯度对当前步骤没有参考价值。
RMProp算法
关于AdaGrad问题的优化方式
针对上述问题,同样可以按照动量法的思路:通过指数加权移动平均法适当地丢弃遥远过去的历史平方梯度。优化后的公式表示如下:
视频中的描述(文章下方链接) 33:14 \text{33:14} 33:14与《深度学习(花书)》中的公式关于 ϵ \epsilon ϵ的位置存在稍许不同,对比如下:
AdaGrad : { G t = ∇ θ ; t − 1 J ( θ t − 1 ) R t = R t − 1 + G t ⊙ G t θ t = θ t − 1 − η R t + ϵ ⊙ G t Video(RMProp) : { G t = ∇ θ ; t − 1 J ( θ t − 1 ) R t = β ⋅ R t − 1 + ( 1 − β ) ⋅ G t ⊙ G t θ t = θ t − 1 − η R t + ϵ ⊙ G t DeepLearning(RMProp) : { G t = ∇ θ ; t − 1 J ( θ t − 1 ) R t = β ⋅ R t − 1 + ( 1 − β ) ⋅ G t ⊙ G t θ t = θ t − 1 − η R t + ϵ ⊙ G t \begin{aligned} \text{AdaGrad : } & \begin{cases} \mathcal G_t = \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \mathcal R_t = \mathcal R_{t-1} + \mathcal G_t \odot \mathcal G_t \\ \begin{aligned} \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\mathcal R_t} + \epsilon} \odot \mathcal G_t \end{aligned} \end{cases} \\ \text{Video(RMProp) : } & \begin{cases} \mathcal G_t = \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \mathcal R_t = \beta \cdot \mathcal R_{t-1} + (1 - \beta) \cdot \mathcal G_t \odot \mathcal G_t \\ \begin{aligned} \theta_t = \theta_{t - 1} - \frac{\eta}{\sqrt{\mathcal R_t} + \epsilon} \odot \mathcal G_t \end{aligned} \end{cases} \\ \text{DeepLearning(RMProp) : } & \begin{cases} \mathcal G_t = \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \mathcal R_t = \beta \cdot \mathcal R_{t-1} + (1 - \beta) \cdot \mathcal G_t \odot \mathcal G_t \\ \begin{aligned} \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\mathcal R_t + \epsilon}} \odot \mathcal G_t \end{aligned} \end{cases} \end{aligned} AdaGrad : Video(RMProp) : DeepLearning(RMProp) : ⎩ ⎨ ⎧Gt=∇θ;t−1J(θt−1)Rt=Rt−1+Gt⊙Gtθt=θt−1−Rt+ϵη⊙Gt⎩ ⎨ ⎧Gt=∇θ;t−1J(θt−1)Rt=β⋅Rt−1+(1−β)⋅Gt⊙Gtθt=θt−1−Rt+ϵη⊙Gt⎩ ⎨ ⎧Gt=∇θ;t−1J(θt−1)Rt=β⋅Rt−1+(1−β)⋅Gt⊙Gtθt=θt−1−Rt+ϵη⊙Gt
这种操作旨在:当执行迭代步骤时,只有之前的若干次迭代步骤对当前步骤产生影响。
RMSProp的算法过程描述
基于 RMSProp \text{RMSProp} RMSProp的算法步骤表示如下:
初始化操作:
- 学习率 η \eta η; 衰减因子 β \beta β;
- 初始化参数 θ \theta θ;梯度累积信息 R = 0 \mathcal R = 0 R=0;超参数 ϵ = 1 0 − 7 \epsilon = 10^{-7} ϵ=10−7
算法过程:
- While \text{While} While没有达到停止准则 do \text{do} do
- 从训练集 D \mathcal D D中采集出包含 k k k个样本的小批量: { ( x ( i ) , y ( i ) ) } i = 1 k \{(x^{(i)},y^{(i)})\}_{i=1}^k {(x(i),y(i))}i=1k;
- 计算当前步骤参数 θ \theta θ的梯度信息 G \mathcal G G:
G ⇐ 1 k ∑ i = 1 k ∇ θ L [ f ( x ( i ) ; θ ) , y ( i ) ] \mathcal G \Leftarrow \frac{1}{k} \sum_{i=1}^k \nabla_{\theta} \mathcal L[f(x^{(i)};\theta),y^{(i)}] G⇐k1i=1∑k∇θL[f(x(i);θ),y(i)] - 使用 R \mathcal R R通过指数加权移动平均法对梯度内积 G ⊙ G \mathcal G \odot \mathcal G G⊙G进行累积:
R ⇐ β ⋅ R + ( 1 − β ) ⋅ G ⊙ G \mathcal R \Leftarrow \beta \cdot \mathcal R + (1 - \beta) \cdot \mathcal G \odot \mathcal G R⇐β⋅R+(1−β)⋅G⊙G - 计算参数 θ \theta θ更新信息 Δ θ \Delta \theta Δθ:
这里暂时使用《深度学习(花书)》中的描述。
Δ θ = − η R t + ϵ ⋅ G \Delta \theta = - \frac{\eta}{\sqrt{\mathcal R_t + \epsilon}} \cdot \mathcal G Δθ=−Rt+ϵη⋅G - 应用更新:
θ ⇐ θ + Δ θ \theta \Leftarrow \theta + \Delta \theta θ⇐θ+Δθ - End While \text{End While} End While
RMSProp示例代码
将 RMSProp \text{RMSProp} RMSProp算法与 AdaGrad \text{AdaGrad} AdaGrad算法进行对比,对应代码表示如下:
import numpy as np
import math
import matplotlib.pyplot as plt
from tqdm import tqdmdef f(x, y):return 0.5 * (x ** 2) + 20 * (y ** 2)def ConTourFunction(x, Contour):return math.sqrt(0.05 * (Contour - (0.5 * (x ** 2))))def Derfx(x):return xdef Derfy(y):return 40 * ydef DrawBackGround(ax,Idx):ContourList = [0.2, 1.0, 4.0, 8.0, 16.0, 32.0]LimitParameter = 0.0001for Contour in ContourList:# 设置范围时,需要满足x的定义域描述。x = np.linspace(-1 * math.sqrt(2 * Contour) + LimitParameter, math.sqrt(2 * Contour) - LimitParameter, 200)y1 = [ConTourFunction(i, Contour) for i in x]y2 = [-1 * j for j in y1]ax[Idx].plot(x, y1, '--', c="tab:blue")ax[Idx].plot(x, y2, '--', c="tab:blue")def Process(mode):assert mode in ["AdaGrad","RMSProp"]Start = (8.0, 1.0)LocList = list()LocList.append(Start)Eta = 0.2Beta = 0.8Epsilon = 0.0000001R = 0.0Delta = 0.1while True:DerStart = (Derfx(Start[0]), Derfy(Start[1]))InnerProduct = (DerStart[0] ** 2) + (DerStart[1] ** 2)if mode == "AdaGrad":R += InnerProductelse:DecayR = R * BetaR = DecayR + ((1.0 - Beta) * InnerProduct)UpdateEta = -1 * (Eta / (Epsilon + math.sqrt(R)))UpdateMessage = (UpdateEta * DerStart[0], UpdateEta * DerStart[1])Next = (Start[0] + UpdateMessage[0], Start[1] + UpdateMessage[1])DerNext = (Derfx(Next[0]), Derfy(Next[1]))# 这里终止条件使用梯度向量的模接近于Delta,一个很小的正值;if math.sqrt((DerNext[0] ** 2) + (DerNext[1] ** 2)) < Delta:breakelse:LocList.append(Next)Start = Nextreturn LocListdef DrawPicture():AdaGradLocList = Process(mode="AdaGrad")RMSPropLocList = Process(mode="RMSProp")fig, ax = plt.subplots(2, 1, figsize=(8, 6))AdaGradplotList = list()ax[0].set_title("AdaGrad")DrawBackGround(ax,Idx=0)for (x, y) in tqdm(AdaGradLocList):AdaGradplotList.append((x, y))ax[0].scatter(x, y, s=30, facecolor="none", edgecolors="tab:orange", marker='o')if len(AdaGradplotList) < 2:continueelse:ax[0].plot([AdaGradplotList[0][0], AdaGradplotList[1][0]], [AdaGradplotList[0][1], AdaGradplotList[1][1]], c="tab:orange")AdaGradplotList.pop(0)RMSPropplotList = list()ax[1].set_title("RMSProp")DrawBackGround(ax, Idx=1)for (x, y) in tqdm(RMSPropLocList):RMSPropplotList.append((x, y))ax[1].scatter(x, y, s=30, facecolor="none", edgecolors="tab:red", marker='o')if len(RMSPropplotList) < 2:continueelse:ax[1].plot([RMSPropplotList[0][0], RMSPropplotList[1][0]], [RMSPropplotList[0][1], RMSPropplotList[1][1]], c="tab:red")RMSPropplotList.pop(0)plt.show()if __name__ == '__main__':DrawPicture()
对应图像结果表示如下:

对比图像可以看出:关于 RMSProp \text{RMSProp} RMSProp的迭代步骤明显少于 AdaGrad \text{AdaGrad} AdaGrad。
回头再次观察 RMSProp \text{RMSProp} RMSProp迭代公式,可以发现:虽然 RMSprop \text{RMSprop} RMSprop算法对 AdaGrad \text{AdaGrad} AdaGrad进行了改进,但其本质上依然是对梯度的大小(学习率)进行优化。下一节我们将对 RMSProp \text{RMSProp} RMSProp进行延伸——从梯度方向、梯度大小(学习率)两个角度同时对梯度进行优化。
即使用 Nesterov \text{Nesterov} Nesterov动量的 RMSProp \text{RMSProp} RMSProp算法。
Reference \text{Reference} Reference
“随机梯度下降、牛顿法、动量法、Nesterov、AdaGrad、RMSprop、Adam”,打包理解对梯度下降的优化
《深度学习(花书)》 P188 8.5.2 RMSProp \text{P188 8.5.2 RMSProp} P188 8.5.2 RMSProp
相关文章:

深度学习笔记之优化算法(六)RMSprop算法的简单认识
深度学习笔记之优化算法——RMSProp算法的简单认识 引言回顾:AdaGrad算法AdaGrad算法与动量法的优化方式区别AdaGrad算法的缺陷 RMProp算法关于AdaGrad问题的优化方式RMSProp的算法过程描述 RMSProp示例代码 引言 上一节对 AdaGrad \text{AdaGrad} AdaGrad算法进行…...

10架构管理之公司整体技术架构
一句话导读 公司的整体技术架构一般是公司的架构组、架构管理部、技术委员会等部门负责,需要对公司整体的技术架构进行把控和管理,确保信息系统的稳定性和可靠性,避免因技术架构不合理而导致的系统崩溃和数据丢失等问题,为公司的业…...

联邦学习综述
《Advances and Open Problems in Federated Learning》 选题:Published 10 December 2019-Computer Science-Found. Trends Mach. Learn. 联邦学习定义 联邦学习是一种机器学习设置,其中多个客户端在中央服务器或服务提供商的协调下协作解决机器学习…...

几行cmd命令,轻松将java文件打包成jar文件
1. 在任意目录下建立一个.java文件 2. 在当前目录下使用cmd命令: javac filename编译 如果报错则使用此命令javac -encoding UTF-8 filename 3.此时已成功生成.class文件 4. 可以手动添加MANIFEST.MF文件 Manifest-Version: 1.0 Main-Class: fileName 5.直接一…...

BuyVM 卢森堡 VPS 测评
description: 发布于 2023-07-05 BuyVM 卢森堡 VPS 测评 产品链接:https://my.frantech.ca/cart.php?gid39 1G口不限流量,续约3个月后升级为10G口突发。抗DMCA版权投诉。抗一般投诉。 大陆连通性还可以,延迟略高,不绕美。 CP…...
JavaScript 编写一个 数值转换函数 万以后简化 例如1000000 展示为 100万 万以下原来数值返回
很多时候 我们看一些系统 能够比较只能的展示过大的数值 例如 到万了 他就能展示出 多少 多少万 看着很奇妙 但实现确实非常的基础 我们只需要一个这样的函数 //数值转换函数 convertNumberToString(num) {//如果传入的数值 不是数字 且也无法转为数字 直接扔0回去if (!parse…...
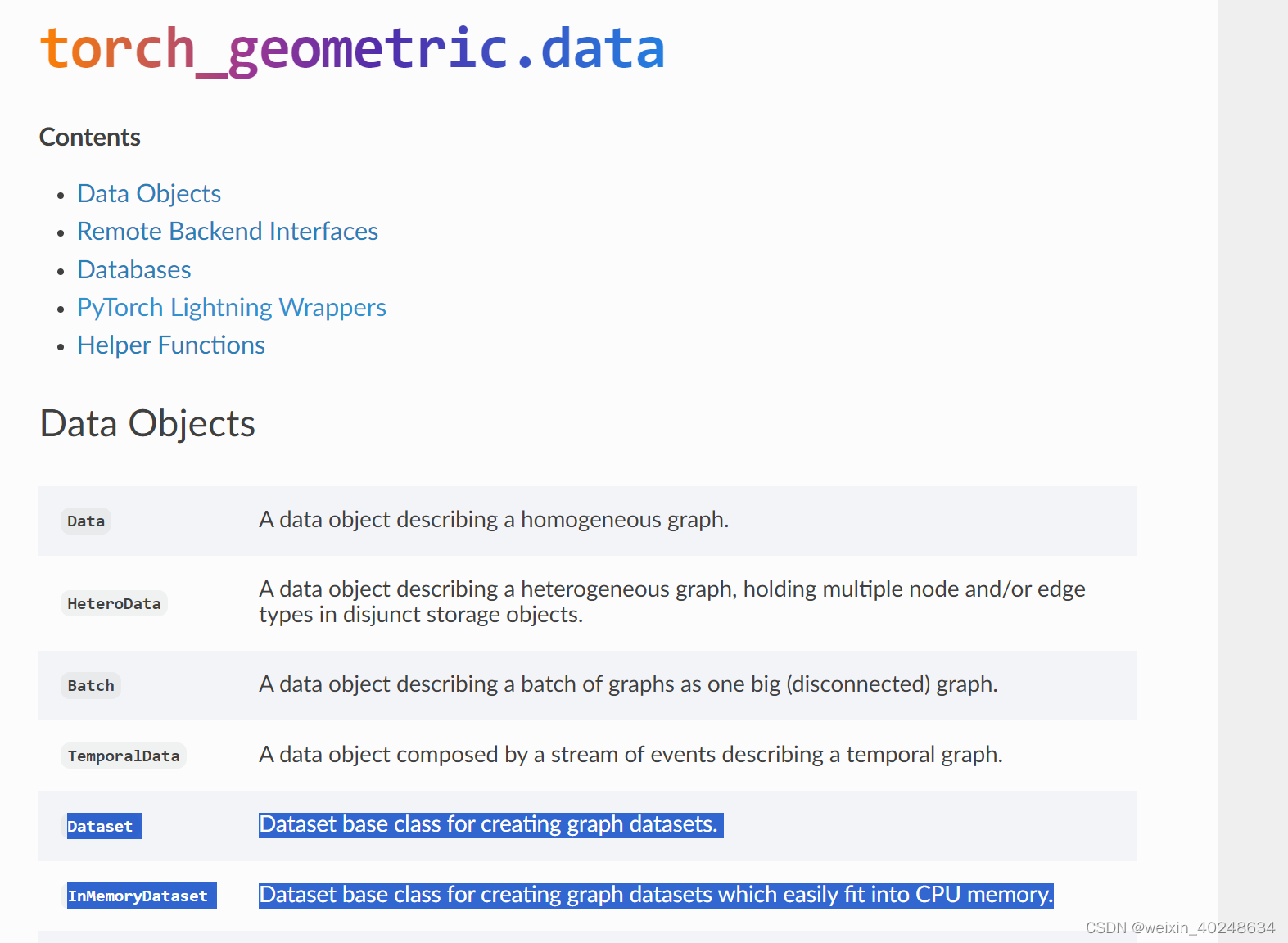
PyG两个data Datsaset v.s. InMemoryDataset
可以看到InMemoryDataset 对CPU更加友好 https://pytorch-geometric.readthedocs.io/en/latest/modules/data.html#pytorch-lightning-wrappers...

ArcGIS Engine:视图菜单的创建和鹰眼图的实现
目录 01 创建项目 1.1 通过ArcGIS-ExtendingArcObjects创建窗体应用 1.2 通过C#-Windows窗体应用创建窗体应用 1.2.1 创建基础项目 1.2.2 搭建界面 02 创建视图菜单 03 鹰眼图的实现 3.1 OnMapReplaced事件的触发 3.2 OnExtentUpdated事件的触发 04 稍作演示 01 创建项目…...
POI 和 EasyExcel 操作 Excel
一、概述 目前操作 Excel 比较流行的就是 Apache POI 和阿里巴巴的 easyExcel。 1.1 POI 简介 Apache POI 是用 Java 编写的免费开源的跨平台的 Java API,Apache POI 提供 API 给 Java 程序对 Microsoft Office 格式文档读和写的常用功能。POI 为 “Poor Obfuscati…...

pytorch算力与有效性分析
pytorch Windows中安装深度学习环境参考文档机器环境说明3080机器 Windows11qt_env 满足遥感CS软件分割、目标检测、变化检测的需要gtrs 主要是为了满足遥感监测管理平台(BS)系统使用的,无深度学习环境内容swin_env 与 qt_env 基本一致od 用于…...

Sublime text启用vim模式
官方教程:https://www.sublimetext.com/docs/vintage.html vintage的github:https://github.com/sublimehq/Vintage...
)
爬虫进阶-反爬破解6(Nodejs+Puppeteer实现登陆官网+实现滑动验证码全自动识别)
一、NodejsPuppeteer实现登陆官网 1.环境说明 Nodejs——直接从官网下载最新版本,并安装 使用npm安装puppeteer:npm install puppeteer npm install xxx -registry https://registry.npm.taobao.org Chromium会自动下载,前提是网络通畅 2.实践操作…...
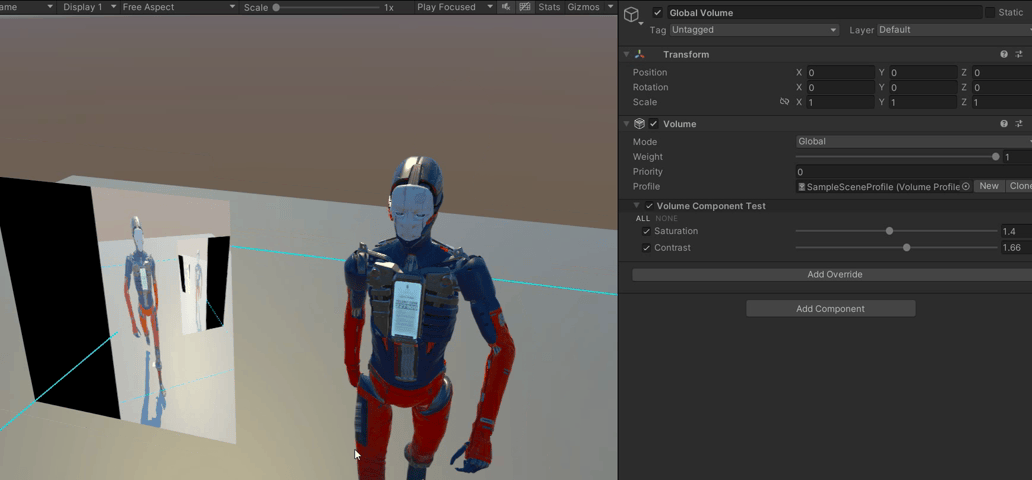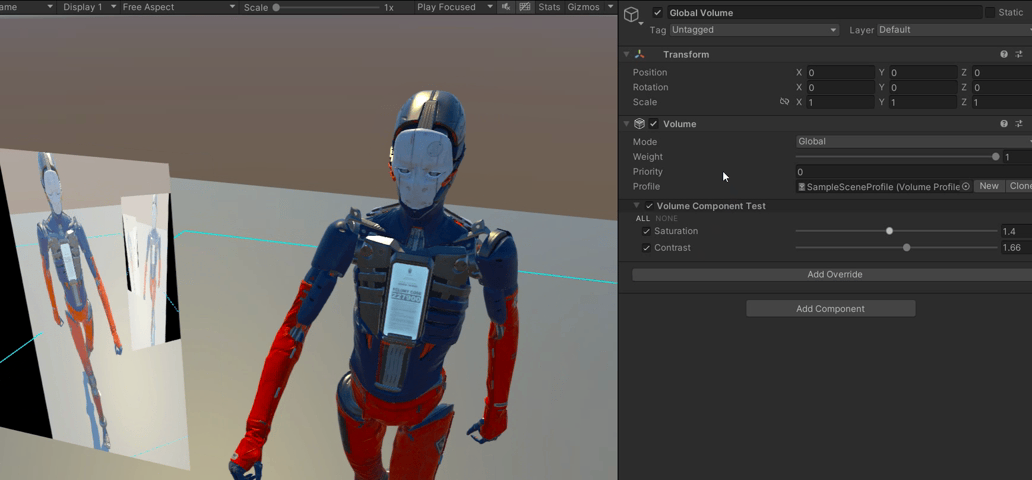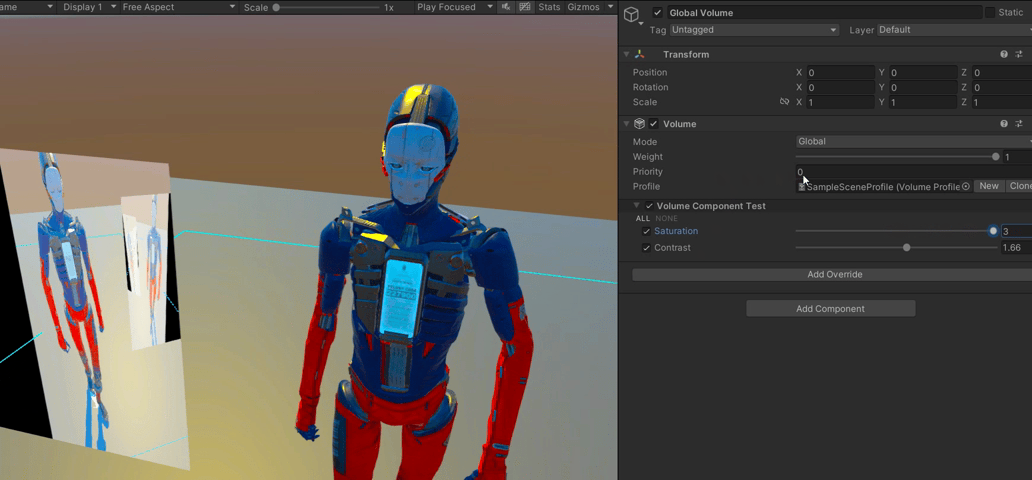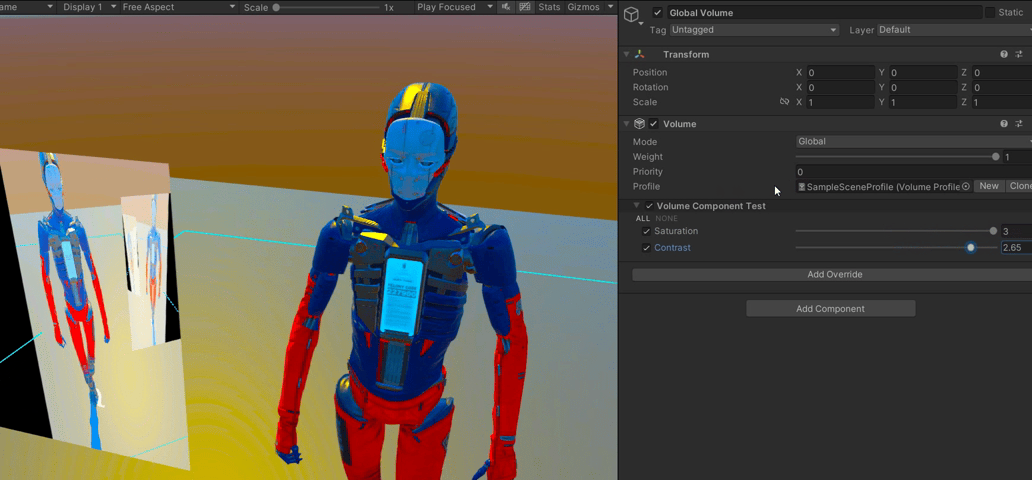
【Unity】RenderFeature笔记
【Unity】RenderFeature笔记 RenderFeature是在urp中添加的额外渲染pass,并可以将这个pass插入到渲染列队中的任意位置。内置渲染管线中Graphics 的功能需要在RenderFeature里实现,常见的如DrawMesh和Blit 可以实现的效果包括但不限于 后处理,可以编写…...
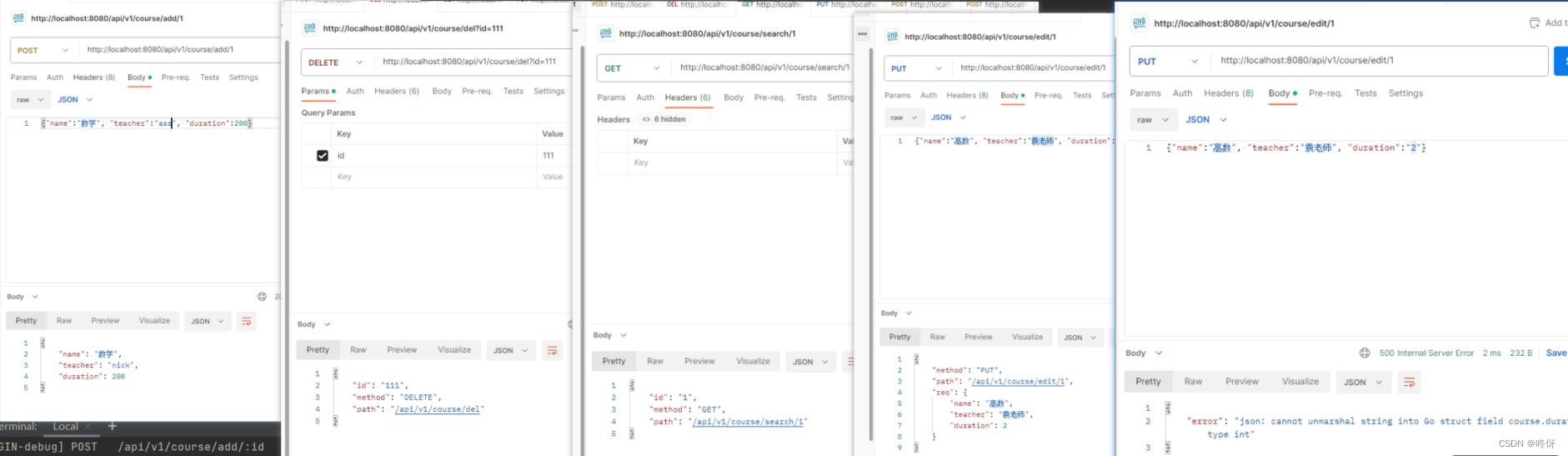
golang gin——controller 模型绑定与参数校验
controller 模型绑定与参数校验 gin框架提供了多种方法可以将请求体的内容绑定到对应struct上,并且提供了一些预置的参数校验 绑定方法 根据数据源和类型的不同,gin提供了不同的绑定方法 Bind, shouldBind: 从form表单中去绑定对象BindJSON, shouldB…...

办公技巧:Excel日常高频使用技巧
目录 1. 快速求和?用 “Alt ” 2. 快速选定不连续的单元格 3. 改变数字格式 4. 一键展现所有公式 “CTRL ” 5. 双击实现快速应用函数 6. 快速增加或删除一列 7. 快速调整列宽 8. 双击格式刷 9. 在不同的工作表之间快速切换 10. 用F4锁定单元格 1. 快速求…...
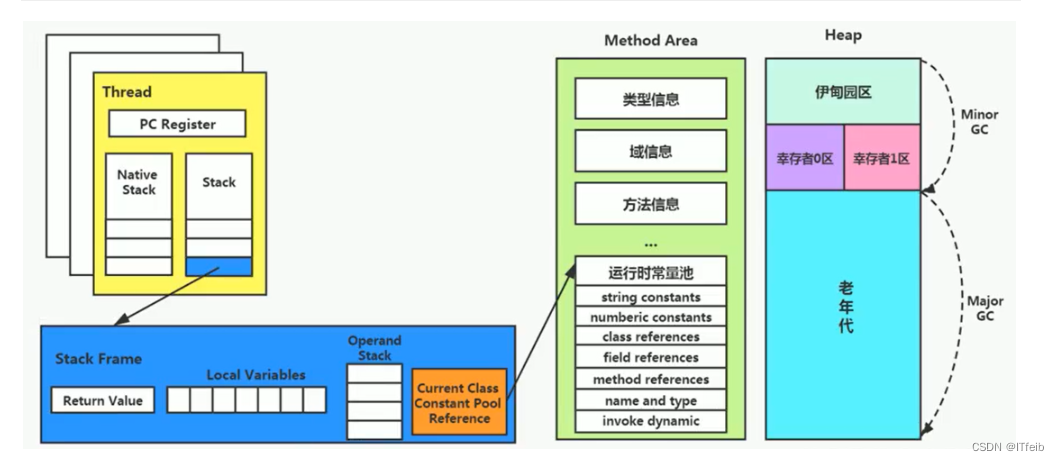
【jvm--方法区】
文章目录 1. 栈、堆、方法区的交互关系2. 方法区的内部结构3. 运行时常量池4. 方法区的演进细节5. 方法区的垃圾回收 1. 栈、堆、方法区的交互关系 方法区的基本理解: 方法区(Method Area)与 Java 堆一样,是各个线程共享的内存区…...

智慧楼宇3D数据可视化大屏交互展示实现了楼宇能源的高效、智能、精细化管控
智慧园区是指将物联网、大数据、人工智能等技术应用于传统建筑和基础设施,以实现对园区的全面监控、管理和服务的一种建筑形态。通过将园区内设备、设施和系统联网,实现数据的传输、共享和响应,提高园区的管理效率和运营效益,为居…...
算法题:摆动序列(贪心算法解决序列问题)
这道题是一道贪心算法题,如果前两个数是递增,则后面要递减,如果不符合则往后遍历,直到找到符合的。(完整题目附在了最后) 代码如下: class Solution(object):def wiggleMaxLength(self, nums):…...

接口自动化测试yaml+requests+allure技术,你学会了吗?
前言 接口自动化测试是在软件开发过程中常用的一种测试方式,通过对接口进行自动化测试,可以提高测试效率、降低测试成本。在接口自动化测试中,yaml、requests和allure三种技术经常被使用。 一、什么是接口自动化测试 接口自动化测试是指通…...

android 获取局域网其他设备ip
Android 通过读取本地Arp表获取当前局域网内其他设备信息_手机查看arp-CSDN博客...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
