式子表达ds类——多用位置/值域表示未知数+区间覆盖转区间加:CF407E
https://www.luogu.com.cn/problem/CF407E
多用位置/值域表示未知数
推出的式子中 n n n 表示长度,应该直接换成 r − l + 1 r-l+1 r−l+1
区间覆盖转区间加
推出的式子有 m x , m n mx,mn mx,mn,朴素思路是用单调队列+区间覆盖维护
那样就不能很方便地维护差
但既然都单调队列了,为什么不直接转区间加呢?
#include<bits/stdc++.h>
using namespace std;
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
#define N 200010
struct Node{int l, r, x; } t;
int n, m, i, j, k, T, d;
stack<Node>q1, q2;
int a[N], lst[N], mn, mx, l, r, rt;
map<int, int>mp; void sol1() {for(i=1; i<=n; ++i) {a[i]=read(); if(i>1 && a[i]!=a[i-1]) j=0; ++j; if(j>mx) mx=j, l=i-mx+1, r=i; }printf("%d %d", l, r);
}struct Segment_tree {int tot, ls[N<<2], rs[N<<2], mn[N<<2], tag[N<<2]; void push_up(int k) {mn[k]=min(mn[ls[k]], mn[rs[k]]); }void jia(int k, int z) {tag[k]+=z; mn[k]+=z; }void push_down(int k) {jia(ls[k], tag[k]); jia(rs[k], tag[k]); tag[k]=0; }void build(int &k, int l, int r) {if(!k) k=++tot; if(l==r) return mn[k]=-d*l, void(); int mid=(l+r)>>1; build(ls[k], l, mid); build(rs[k], mid+1, r); push_up(k); }void add(int k, int l, int r, int x, int y, int z) {if(l>=x && r<=y) return jia(k, z), void(); int mid=(l+r)>>1; push_down(k); if(x<=mid) add(ls[k], l, mid, x, y, z); if(y>=mid+1) add(rs[k], mid+1, r, x, y, z); push_up(k); }int que(int k, int l, int r, int x, int y, int z) {if(l>=x && r<=y && mn[k]>z) return -1; if(l==r) return mn[k]<=z ? l : -1; int mid=(l+r)>>1, flg=-1; push_down(k); if(y>=mid+1) flg=que(rs[k], mid+1, r, x, y, z); if(flg!=-1) return flg; return que(ls[k], l, mid, x, y, z); }
}Seg;signed main()
{n=read(); m=read(); d=read(); if(d==0) return sol1(), 0; for(i=1; i<=n; ++i) {a[i]=read(); lst[i]=n; if(mp[a[i]]) lst[mp[a[i]]]=i-1; mp[a[i]]=i; }for(i=2; i<=n; ++i) if(abs(a[i]-a[i-1])%d) lst[i-1]=i-1; for(i=n-1; i>=1; --i) lst[i]=min(lst[i], lst[i+1]); Seg.build(rt, 1, n); for(i=n, j=0; i>=1; --i) {l=r=i; while(!q1.empty() && a[i]>=q1.top().x) {t=q1.top(); q1.pop(); r=t.r; Seg.add(1, 1, n, t.l, t.r, -t.x); }q1.push({l, r, a[i]}); Seg.add(1, 1, n, l, r, a[i]); l=r=i; while(!q2.empty() && a[i]<=q2.top().x) {t=q2.top(); q2.pop(); r=t.r; Seg.add(1, 1, n, t.l, t.r, t.x); }q2.push({l, r, a[i]}); Seg.add(1, 1, n, l, r, -a[i]); k=Seg.que(1, 1, n, i, lst[i], d*m-d*i); if(k-i+1>=mx) mx=k-i+1, j=i; }printf("%d %d", j, j+mx-1); return 0;
}相关文章:

式子表达ds类——多用位置/值域表示未知数+区间覆盖转区间加:CF407E
https://www.luogu.com.cn/problem/CF407E 多用位置/值域表示未知数 推出的式子中 n n n 表示长度,应该直接换成 r − l 1 r-l1 r−l1 区间覆盖转区间加 推出的式子有 m x , m n mx,mn mx,mn,朴素思路是用单调队列区间覆盖维护 那样就不能很方便…...
)
Python 实现秒表功能(比较好玩的题目)
以下实例使用 time 模块来实现秒表功能: import time print(按下回车开始计时,按下ctrlc停止计时) while True:input("")starttimetime.time()print(开始)try:while True:print(计时:,round(time.time()-starttime,0),秒)time.sle…...

DALL-E 3调参教程;百度新出的AI写小说神器;通义听悟看播客也太爽了;系列博文带你理解生成式AI | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🔥 2023年诺贝尔奖全部揭晓,一文看完6类奖项花落谁家 https://www.nobelprize.org/prizes 随着最后一项「经济学奖」的揭秘&a…...

设计模式-享元模式
概念 共享内存(主要考虑内存,而非效率)相同的数据,共享使用(JS中未找到经典应用场景) 演示 <!-- 无限下拉列表,将事件代理到高层节点上 --> <!-- 如果都绑定到<a>标签&#x…...

中秋时节赏明月,五子棋戏月饼趣 — Flutter中秋限定版五子棋
前言 当中秋时节来临,我们都期待着与亲人朋友共度这个美好的节日。这个时候,除了传统的赏月和品尝美味的月饼,我还有一个特别的建议——尝试一款有趣的Flutter五子棋游戏!这款五子棋游戏以中秋为主题,游戏的棋子也可爱…...
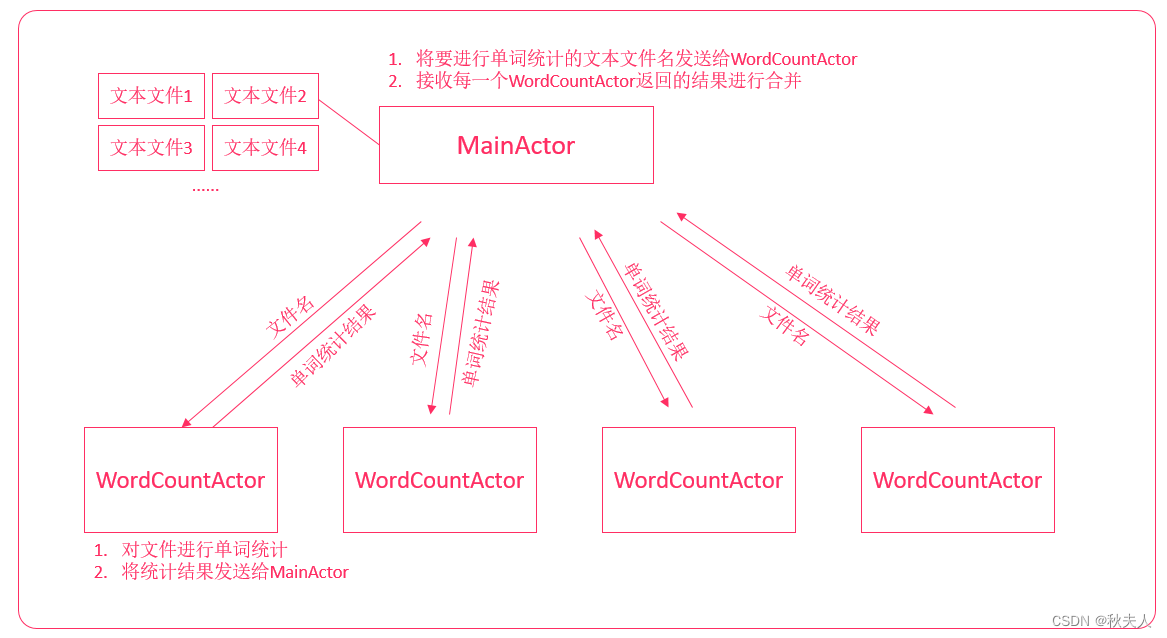
Scala第十九章节
Scala第十九章节 scala总目录 文档资料下载 章节目标 了解Actor的相关概述掌握Actor发送和接收消息掌握WordCount案例 1. Actor介绍 Scala中的Actor并发编程模型可以用来开发比Java线程效率更高的并发程序。我们学习Scala Actor的目的主要是为后续学习Akka做准备。 1.1 Ja…...

kafka与hbase的区别
Kafka 和 HBase 是两个不同的分布式数据存储系统,它们可以在大数据应用中发挥不同的作用。 Kafka 是一个高吞吐量的分布式发布订阅消息系统,主要用于处理实时数据流。它具有以下特点: 高性能:Kafka 能够以非常高的吞吐量和低延迟…...

出栈序列的合法性
给定一个最大容量为 M 的堆栈,将 N 个数字按 1, 2, 3, ..., N 的顺序入栈,允许按任何顺序出栈,则哪些数字序列是不可能得到的?例如给定 M5、N7,则我们有可能得到{ 1, 2, 3, 4, 5, 6, 7 },但不可能得到{ 3, …...
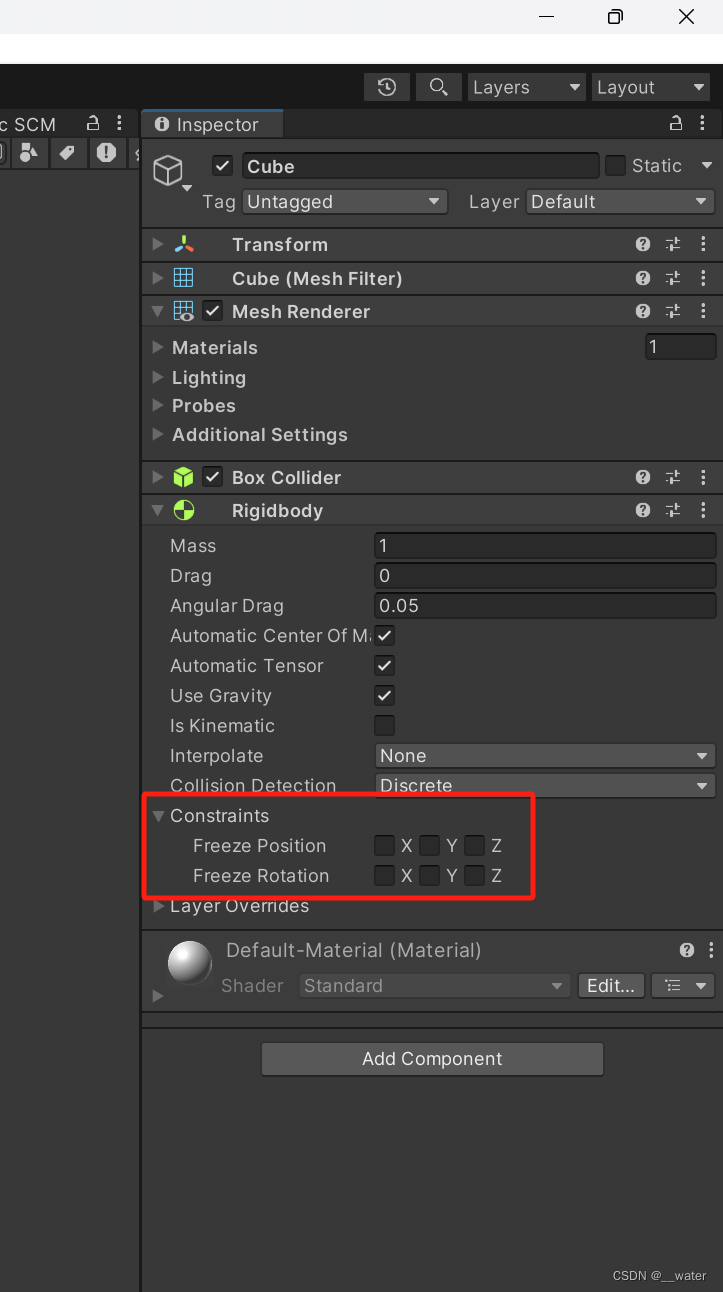
unity操作_刚体 c#
刚体Rigidbody 首先在场景中创建一个Plane 位置重置一下 再创建一个Cube 充值 y0.5 我们可以看出创建的Cube 和 Plane都自带碰撞器 Plane用的是网格碰撞器 我们可以通过网格世界看到不同的网格碰撞器 发生碰撞(条件): 两个物体都有碰撞器 …...
介绍(Python示例))
网络编程中套接字(socket)介绍(Python示例)
网络编程中套接字(socket)介绍(Python示例) 网络编程就是同一计算机的进程间或者不同的联网计算机之间的通信(交换数据)。 那么,这两台计算机之间用什么传输数据呢?首先你肯定先需要…...

d3dcompiler_43.dll是什么文件?缺失d3dcompiler_43.dll文件修复与解决方法
今天我要和大家分享的是关于d3dcompiler_43.dll丢失的解决方法。我相信很多网友在使用电脑时都遇到过这个问题,那么接下来就让我们一起来探讨一下如何解决这个问题吧! 首先,让我们来了解一下d3dcompiler_43.dll文件的总体介绍。d3dcompiler_…...

YOLOv7改进:SPD-Conv,低分辨率图像和小物体涨点明显,涨点神器!!!
💡💡💡本文属于原创独家改进:SPD-Conv,优势:处理低分辨率图像和小物体等更困难的任务时性能更优 SPD-Conv | 亲测在多个数据集实现暴力涨点,尤其是小物体检测你值得拥有,强烈推荐,独家首发; 收录: YOLOv7高阶自研专栏介绍: http://t.csdnimg.cn/tYI0c ✨…...
连接mysql数据库)
iris(golang)连接mysql数据库
连接mysql数据库 安装依赖 go get github.com/go-sql-driver/mysqlfunc LinkMySQL(){DB,_ : sql.Open("mysql","root:123456tcp(127.0.0.1:3306)/webgo_accout")//设置数据库最大连接数DB.SetConnMaxLifetime(100)//设置上数据库最大闲置连接数DB.SetMaxId…...
笔记)
C现代方法(第1、2章)笔记
文章目录 C现代方法笔记(chapter1&2)序言0.1 C标准0.2 现代方法 第1章 C语言概述1.1 C语言的历史1.1.1 起源1.1.2 标准化1.1.3 基于C的语言 1.2 C语言的优缺点1.2.1 C语言的优点1.2.2 C语言的缺点1.2.3 高效地使用C语言 第2章 C语言基本概念2.1 编写…...

练[CISCN2019 华东南赛区]Double Secret
[CISCN2019 华东南赛区]Double Secret 文章目录 [CISCN2019 华东南赛区]Double Secret掌握知识解题思路关键paylaod 掌握知识 flask框架报错源码泄露,使用脚本进行RC4加解,ssti使用内置函数进行模板注入 解题思路 打开网站链接,页面就一…...

『Linux - gcc / g++』c程序翻译过程
文章目录 前言预处理 -E编译 -S汇编 -c链接动静态链接 前言 在计算机中的每一个程序是由代码变化而来的,但是事实上来说,用 c/C 写出的代码是不能被计算机识别的,其中必须经过一系列的过程才能使这个代码能成功的被计算机识别; …...

苹果遭遇安全危机,应用商店曝出不良APP,或影响iPhone的销售
据澎湃新闻报道指苹果的App Store被曝出不良APP位居下载榜前列,这对于向来强调APP严格审核的苹果来说是巨大的打击,更影响向来被认为信息安全遥遥领先的名声,对当下正热销的iPhone15或造成打击。 据了解被曝的软件以“学习XX字母”为命名&…...
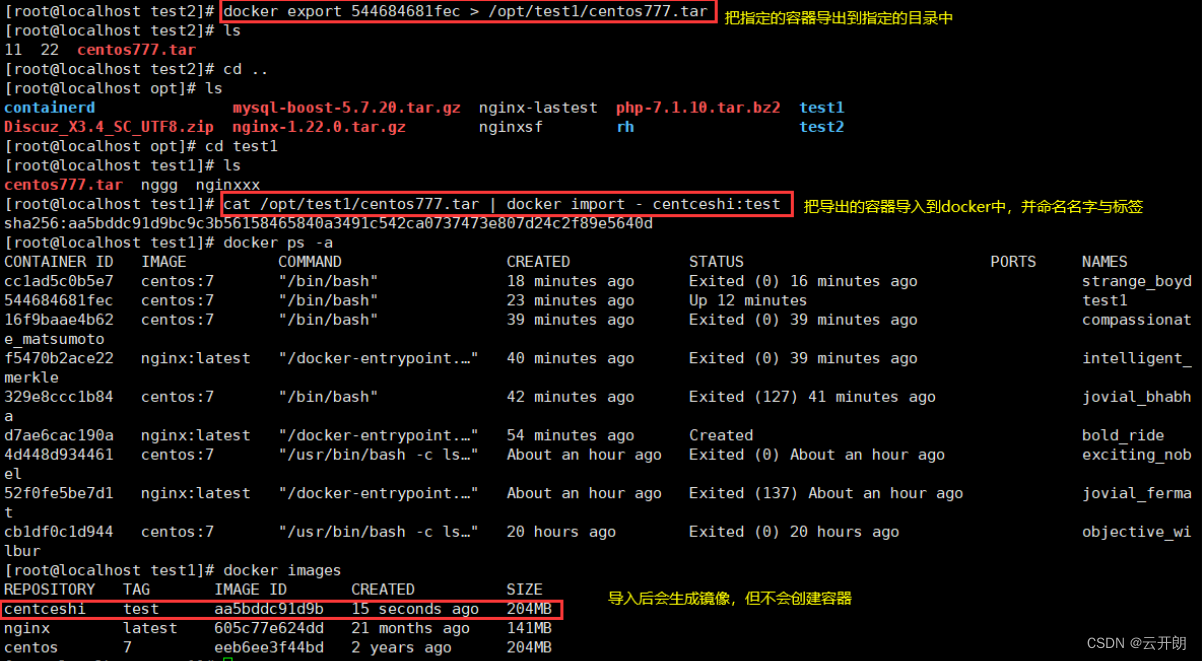
docker 基本操作
一、docker 概述 Docker是一个开源的应用容器引擎,基于go语言开发并遵循了apache2.0协议开源。 Docker是在Linux容器里运行应用的开源工具,是一种轻量级的“虚拟机”。 Docker 的容器技术可以在一台主机上轻松为任何应用创建一个轻量级的、可移植的、自…...

ARM:使用汇编完成三个灯流水亮灭
1.汇编源代码 .text .global _start _start: 设置GPIOF寄存器的时钟使能LDR R0,0X50000A28LDR R1,[R0]ORR R1,R1,#(0x1<<5)STR R1,[R0]设置GPIOE寄存器的时钟使能LDR R0,0X50000A28LDR R1,[R0] 从r0为起始地址的4字节数据取出放在R1ORR R1,R1,#(0x1<<4) 第4位设…...
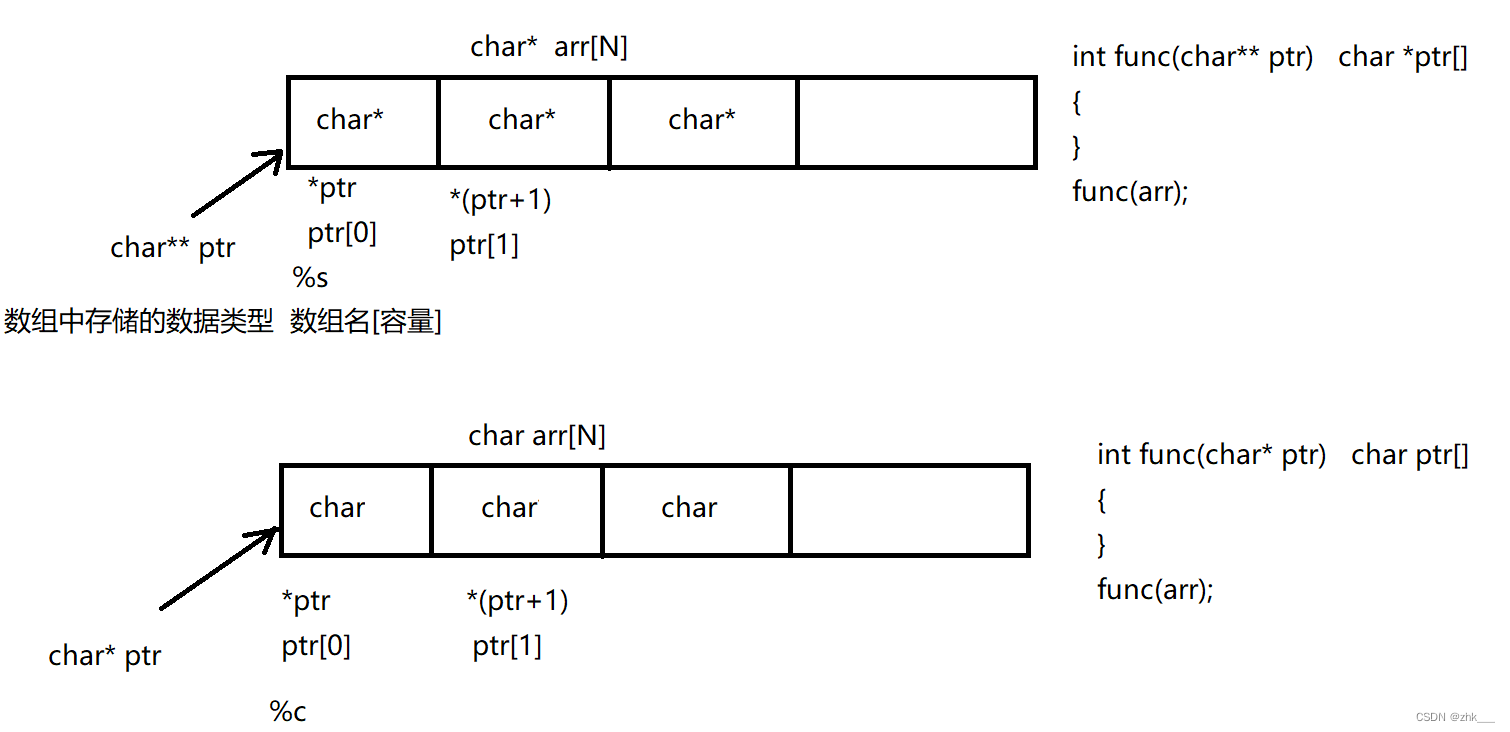
嵌入式养成计划-33--数据库-sqlite3
七十一、 数据库 71.1 数据库基本概念 数据(Data) 能够输入计算机并能被计算机程序识别和处理的信息集合数据库 (Database)数据库是在数据库管理系统管理和控制之下,存放在存储介质上的数据集合 常用的数据库 大型数…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
