算法练习11——买卖股票的最佳时机 II
LeetCode 122 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
问题转换 + 贪心
只要明天比今天价格高就在今天买入明天卖出,吃掉所有收益一定能达成题意要求的收益
class Solution:def maxProfit(self, prices: List[int]) -> int:res = 0if len(prices) == 1:return resfor i in range(1, len(prices)):tmp = prices[i] - prices[i - 1]res += (tmp if tmp > 0 else 0)return res
动态规划
下面网友写的题解十分精彩,从状态转移方程可以看出计算i只需i-1,可以进行滚动优化
作者:liweiwei1419
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/solutions/38498/tan-xin-suan-fa-by-liweiwei1419-2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
第 1 步:定义状态
状态 dp[i][j] 定义如下:
dp[i][j] 表示到下标为 i 的这一天,持股状态为 j 时,我们手上拥有的最大现金数。
注意:限定持股状态为 j 是为了方便推导状态转移方程,这样的做法满足 无后效性。
其中:
第一维 i 表示下标为 i 的那一天( 具有前缀性质,即考虑了之前天数的交易 );
第二维 j 表示下标为 i 的那一天是持有股票,还是持有现金。这里 0 表示持有现金(cash),1 表示持有股票(stock)。
第 2 步:思考状态转移方程
状态从持有现金(cash)开始,到最后一天我们关心的状态依然是持有现金(cash);
每一天状态可以转移,也可以不动。状态转移用下图表示:

(状态转移方程写在代码中)
说明:
由于不限制交易次数,除了最后一天,每一天的状态可能不变化,也可能转移;
写代码的时候,可以不用对最后一天单独处理,输出最后一天,状态为 0 的时候的值即可。
第 3 步:确定初始值
起始的时候:
如果什么都不做,dp[0][0] = 0;
如果持有股票,当前拥有的现金数是当天股价的相反数,即 dp[0][1] = -prices[i];
第 4 步:确定输出值
终止的时候,上面也分析了,输出 dp[len - 1][0],因为一定有 dp[len - 1][0] > dp[len - 1][1]。
public class Solution {public int maxProfit(int[] prices) {int len = prices.length;if (len < 2) {return 0;}// 0:持有现金// 1:持有股票// 状态转移:0 → 1 → 0 → 1 → 0 → 1 → 0int[][] dp = new int[len][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < len; i++) {// 这两行调换顺序也是可以的dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);}return dp[len - 1][0];}
}
复杂度分析:
时间复杂度:O(N),这里 N 表示股价数组的长度;
空间复杂度:O(N),虽然是二维数组,但是第二维是常数,与问题规模无关。
相关文章:

算法练习11——买卖股票的最佳时机 II
LeetCode 122 买卖股票的最佳时机 II 给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。 在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。 返回…...

linux——多线程,线程控制
目录 一.POSIX线程库 二.线程创建 1.创建线程接口 2.查看线程 3.多线程的健壮性问题 4.线程函数参数传递 5.线程id和地址空间 三.线程终止 1.pthread_exit 2.pthread_cancel 四.线程等待 五.线程分离 一.POSIX线程库 站在内核的角度,OS只有轻量级进程…...
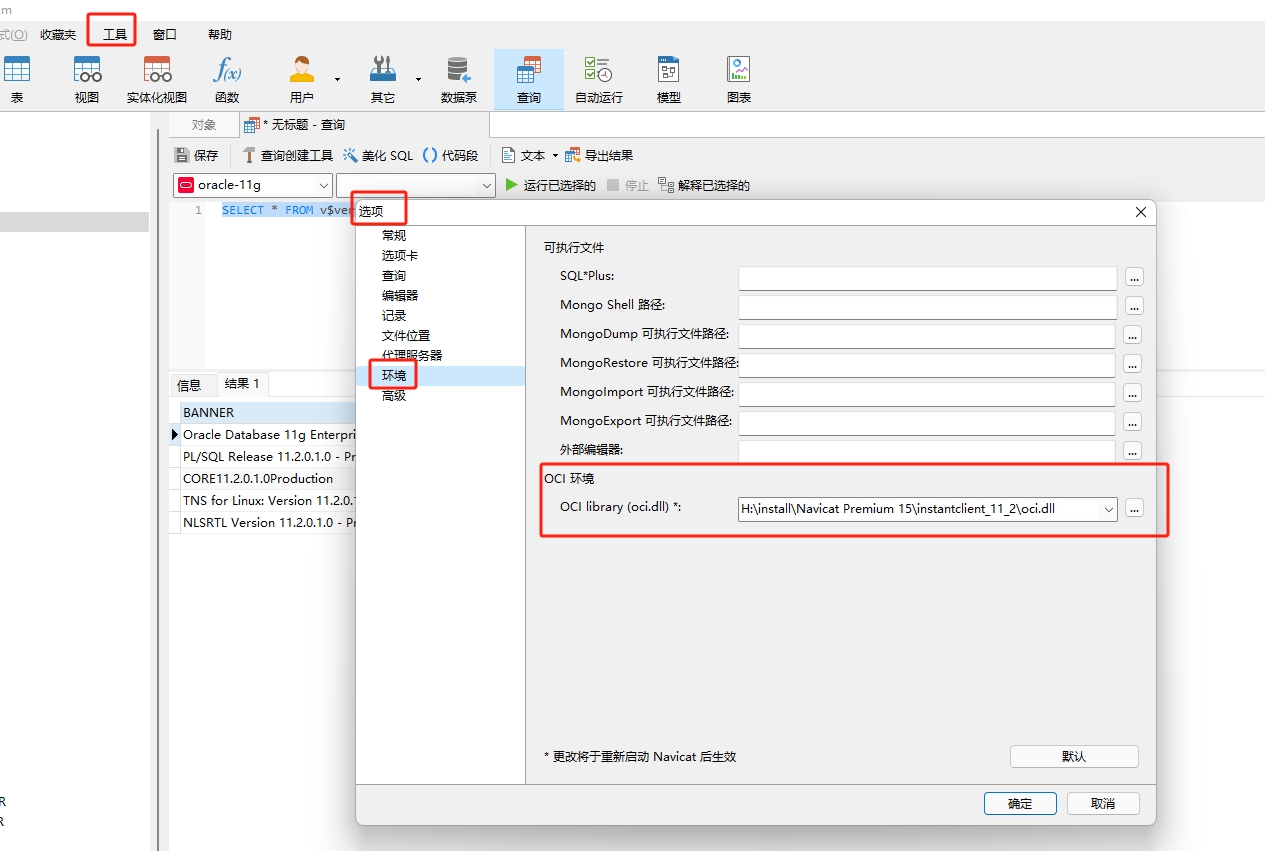
Oracle 简介与 Docker Compose部署
最近,我翻阅了在之前公司工作时的笔记,偶然发现了一些有关数据库的记录。当初,我们的项目一开始采用的是 Oracle 数据库,但随着项目需求的变化,我们不得不转向使用 SQL Server。值得一提的是,公司之前采用的…...

mp4音视频分离技术
文章目录 问题描述一、分离MP3二、分离无声音的MP4三、结果 问题描述 MP4视频想拆分成一个MP3音频和一个无声音的MP4文件 一、分离MP3 ffmpeg -i C:\Users\Administrator\Desktop\一个文件夹\我在财神殿里长跪不起_完整版MV.mp4 -vn C:\Users\Administrator\Desktop\一个文件…...

JVM 参数
JVM 参数类型大致分为以下几类: 标准参数(-):保证在所有的 JVM 实现都支持的参数非标准参数(-X):通用的,特定于 HotSpot 虚拟机的参数,这些参数不保证在所有 JVM 实现中…...

黑马点评-07缓存击穿问题(热点key失效)及解决方案,互斥锁和设置逻辑过期时间
缓存击穿问题(热点key失效) 缓存击穿问题也叫热点Key问题,就是一个被高并发访问并且重建缓存业务较复杂的key突然失效了,此时无数的请求访问会在瞬间打到数据库,带来巨大的冲击 一件秒杀中的商品的key突然失效了,由于大家都在疯狂抢购那么这个瞬间就会有无数的请求…...

信息系统项目管理师第四版学习笔记——项目进度管理
项目进度管理过程 项目进度管理过程包括:规划进度管理、定义活动、排列活动顺序、估算活动持续时间、制订进度计划、控制进度。 规划进度管理 规划进度管理是为规划、编制、管理、执行和控制项目进度而制定政策、程序和文档的过程。本过程的主要作用是为如何在…...

指挥棒:C++ 与运算符
文章目录 参考描述算术运算符除法运算取模运算复合赋值运算符自增运算符自减运算符 比较运算符逻辑运算符概念短路为什么需要短路机制? 参考 项目描述微软C 语言文档搜索引擎Bing、GoogleAI 大模型文心一言、通义千问、讯飞星火认知大模型、ChatGPTC Primer Plus &…...
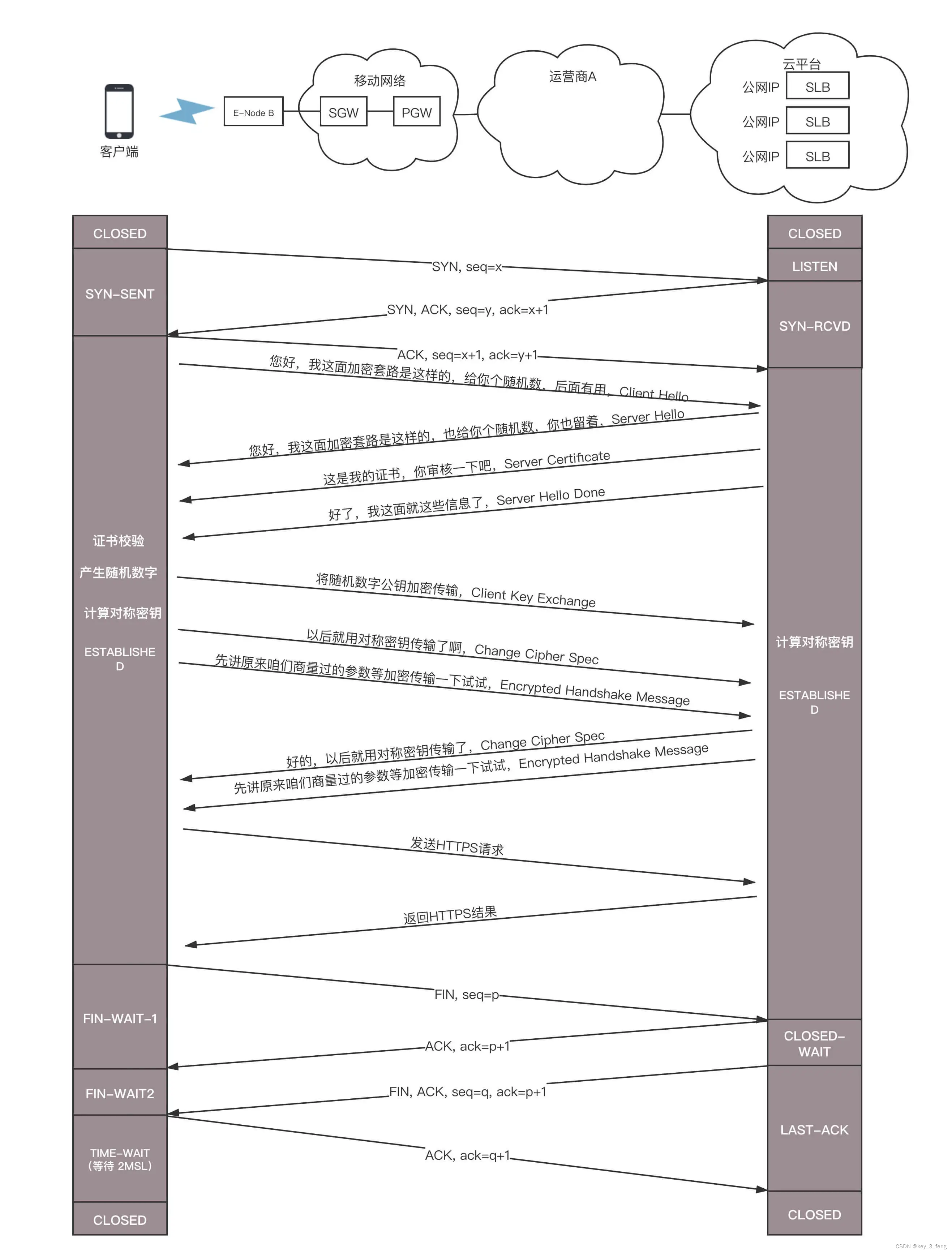
HTTPS建立连接的过程
HTTPS 协议是基于 TCP 协议的,因而要先建立 TCP 的连接。在这个例子中,TCP 的连接是在手机上的 App 和负载均衡器 SLB 之间的。 尽管中间要经过很多的路由器和交换机,但是 TCP 的连接是端到端的。TCP 这一层和更上层的 HTTPS 无法看到中间的包…...

Python接口自动化搭建过程,含request请求封装!
开篇碎碎念 接口测试自动化好处 显而易见的好处就是解放双手😀。 可以在短时间内自动执行大量的测试用例通过参数化和数据驱动的方式进行测试数据的变化,提高测试覆盖范围快速反馈测试执行结果和报告支持持续集成和持续交付的流程 使用Requestspytes…...
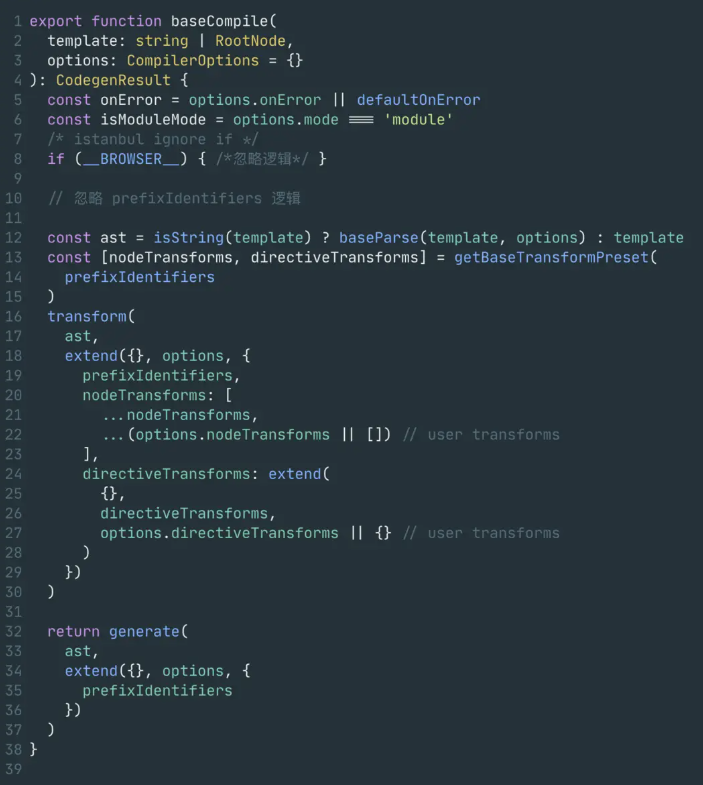
Vue3 编译原理
文章目录 一、编译流程1. 解读入口文件 packgages/vue/index.ts2. compile函数的运行流程 二、AST 解析器1. ast 的生成2. 创建ast的根节点3. 解析子节点 parseChildren(关键)4. 解析模版元素 Element模版元素解析-举例分析 一、编译流程 1. 解读入口文…...

spring boot整合Minio
MinIO 安装MinIo # 先创建minio 文件存放的位置 mkdir -p /opt/docker/minio/data# 启动并指定端口 docker run \-p 9000:9000 \-p 5001:5001 \--name minio \-v /opt/docker/minio/data:/data \-e "MINIO_ROOT_USERminioadmin" \-e "MINIO_ROOT_PASSWORDmini…...
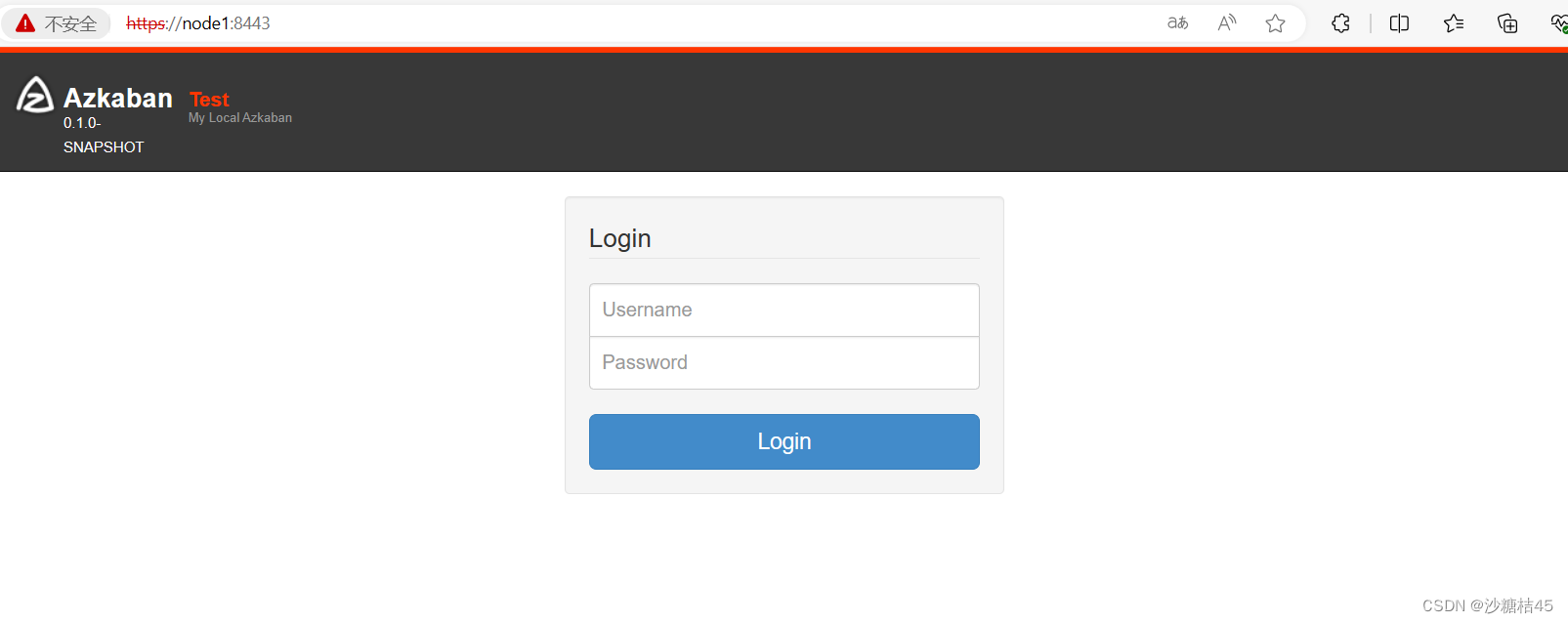
Hadoop----Azkaban的使用与一些报错问题的解决
1.因为官方只放出源码,并没有放出其tar包,所以需要我们自己编译,通过查阅资料我们可以使用gradlew对其进行编译,还是比较简单,然后将里面需要用到的服务文件夹进行拷贝,完善其文件夹结构,通常会…...
「新房家装经验」客厅电视高度标准尺寸及客厅电视机买多大尺寸合适?
客厅电视悬挂高度标准尺寸是多少? 客厅电视悬挂高度通常在90~120厘米之间,电视挂墙高度也可以根据个人的喜好和实际情况来调整,但通常不宜过高,以坐在沙发上观看时眼睛能够平视到电视中心点或者中心稍微往下一点的位置为适宜。 客…...

ArduPilot开源飞控之AP_Baro_DroneCAN
ArduPilot开源飞控之AP_Baro_DroneCAN 1. 源由2. back-end抽象类3. 方法实现3.1 probe3.2 update3.3 subscribe_msgs3.4 handle_pressure/handle_temperature3.5 CAN port 4. 参考资料 1. 源由 鉴于ArduPilot开源飞控之AP_Baro中涉及Sensor Driver有以下总线类型: …...
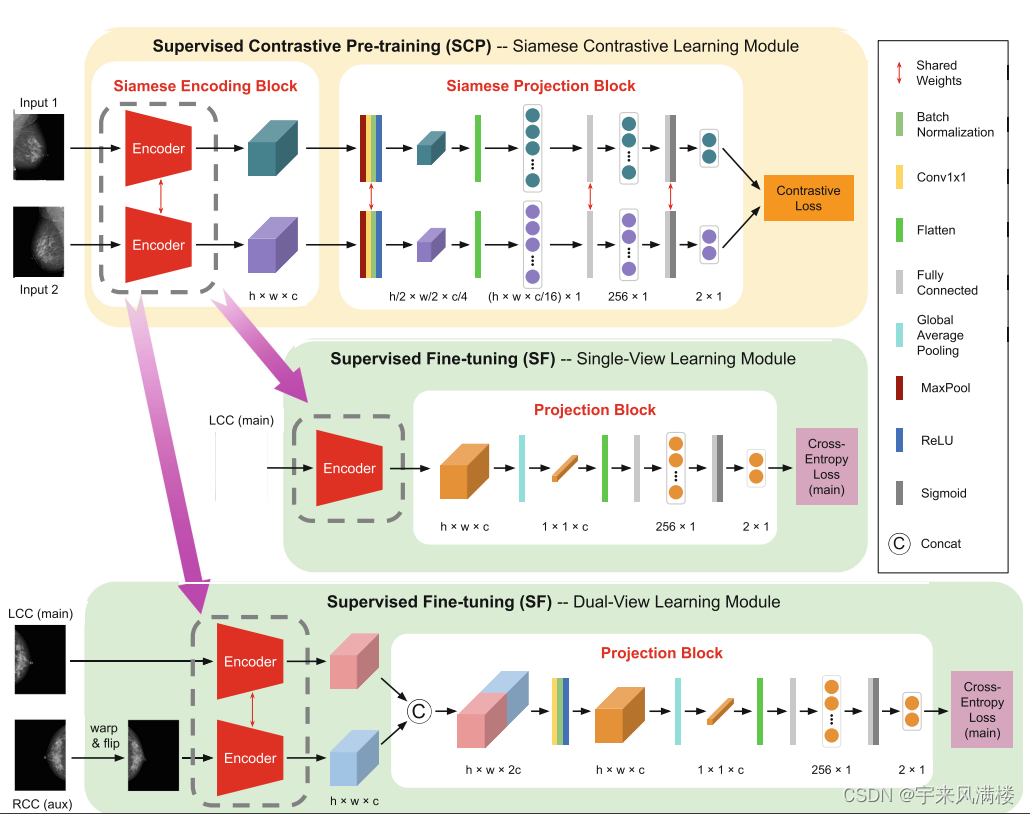
Supervised Contrastive Pre-training for Mammographic Triage Screening Model
方法 品红色箭头表示将生成的孪生编码器分别迁移到单视角学习模块和双视角学习模块...

JVM技术文档--JVM优化思路以及问题定位--JVM可调整参数汇总
阿丹: 一个优秀的程序员,是因为在线上的排查以及遇到的线上、生产事故较多所以定位问题以及解决问题会比普通程序员快很多,所以一个优秀的程序员要逐渐形成自己的方法论,来完善和解决问题。 我们是如何发现问题的呢? …...

Oracle10g数据库迁移方案
试验了很多次Oracle数据库迁移才成功,贴出来给大家参考一下,我看到有的地方写迁移之后还需要重新建立temp表空间,这个还没有研究。另外说一点的是两个数据库的版本一定要一致,之前失败过一次,就是因为两个数据库的版本…...

备忘录模式:对象状态的保存与恢复
欢迎来到设计模式系列的第十八篇文章,本篇将介绍备忘录模式。备忘录模式是一种行为型设计模式,它允许在不破坏封装性的前提下捕获一个对象的内部状态,并在之后恢复该状态。这种模式通常用于需要提供撤销操作的情况。 什么是备忘录模式&#…...

C# InvokeRequired线程安全
C# InvokeRequired线程安全 为了保证新家的线程可能要对主界面的控件元素的属性发生一些改变,此时防止此操作对于主线程的影响,就提出了 InvokeRequired方法,保证主线程的安全,同时新加的线程也可以改变主页面中元素的值。 定义…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
