C# InvokeRequired线程安全
C# InvokeRequired线程安全
为了保证新家的线程可能要对主界面的控件元素的属性发生一些改变,此时防止此操作对于主线程的影响,就提出了 InvokeRequired方法,保证主线程的安全,同时新加的线程也可以改变主页面中元素的值。
定义一个方法来使用:
public static void InvokeIfRequired<T>(this T control, Action<T> action) where T : ISynchronizeInvoke
{if (control.InvokeRequired){control.BeginInvoke(new Action(() => action(control)), null);}else{action(control);}
}
使用方法:
this.TextBox1.InvokeIfRequired(rsb =>{rsb.Text = str1; });
其中的TextBox1就是我们所使用的其中一个控件,通过新增的线程对他操作;
如果有更好的办法,欢迎同道中人可以相互交流
相关文章:

C# InvokeRequired线程安全
C# InvokeRequired线程安全 为了保证新家的线程可能要对主界面的控件元素的属性发生一些改变,此时防止此操作对于主线程的影响,就提出了 InvokeRequired方法,保证主线程的安全,同时新加的线程也可以改变主页面中元素的值。 定义…...
pdf怎么转成jpg图片格式
pdf怎么转成jpg图片格式?对于大家平时在工作或者生活中的图片使用习惯,经常需要将各种格式的文件转换成易于浏览和使用的JPG格式图片以便保存。如今,因为pdf文件具有更强的稳定性和设备兼容性,PDF文件在平时的电脑使用过程中可以说…...
React +ts + babel+webpack
babel babel/preset-typescript 专门处理ts "babel/cli": "^7.17.6", "babel/core": "^7.17.8", "babel/preset-env": "^7.16.11", "babel/preset-react": "^7.16.7", "babel/preset…...
红队专题-REVERSE二进制逆向反编译
红队专题 招募六边形战士队员IDA pro安装python2加入环境变量py2安装pip安装IDA 7.0 proIDAPython: importing "site" failed. 招募六边形战士队员 一起学习 代码审计、安全开发、web攻防、逆向等。。。 私信联系 IDA pro 安装python2 python-2.7.3.msi 加入环…...

Spring技术原理之Bean生命周期原理解析
Spring技术原理之Bean生命周期原理解析 Spring作为Java领域中的优秀框架,其核心功能之一是依赖注入和生命周期管理。其中,Bean的生命周期管理是Spring框架中一个重要的概念。在本篇文章中,我们将深入探讨Spring技术原理中的Bean生命周期原理…...
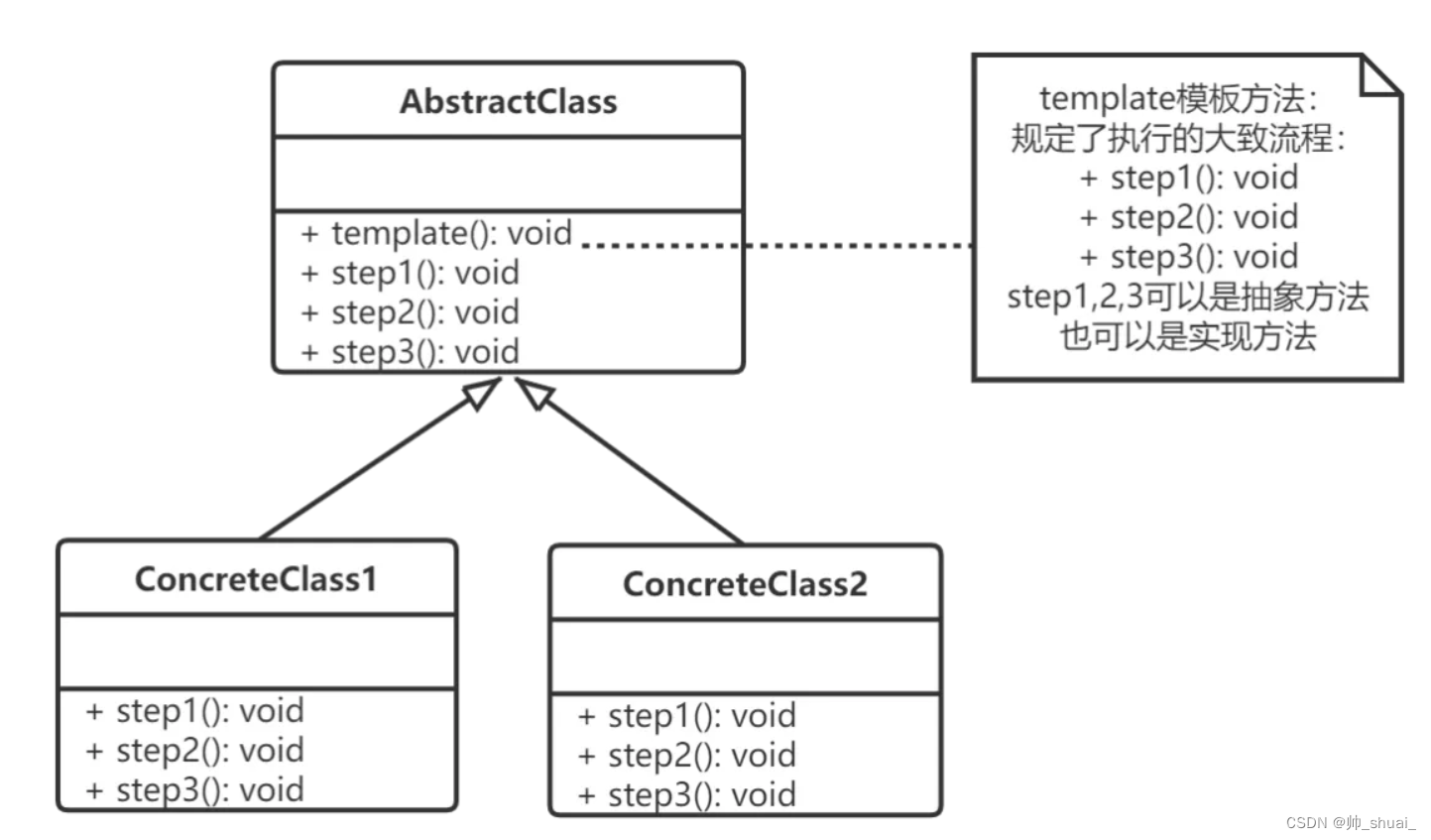
Unity实现设计模式——模板方法模式
Unity实现设计模式——模板方法模式 模板模式(Template Pattern), 指在一个抽象类公开定义了执行它的方法的模板。它的子类可以按需要重写方法实现,但调用将以抽象类中定义的方式进行。 简单说, 模板方法模式定义一个操作中的算法的骨架&…...
)
C++实现高性能内存池(二)
文章目录 一、设计内存池二、实现MemoryPool::construct() 实现MemoryPool::deallocate() 实现MemoryPool::~MemoryPool() 实现MemoryPool::allocate() 实现三、与 std::vector 的性能对比一、设计内存池 在上节中,我们在模板链表栈中使用了默认构造器来管理栈操作中的元素内…...

沪深300期权一个点多少钱?
经中国证监会批准,深圳证券交易所于2019年12月23日上市嘉实沪深300ETF期权合约品种。该产品是以沪深300为标的物的嘉实沪深300ETF交易型指数基金为标的衍生的标准化合约,下文介绍沪深300期权一个点多少钱?本文来自:期权酱 一、沪深300期权涨…...
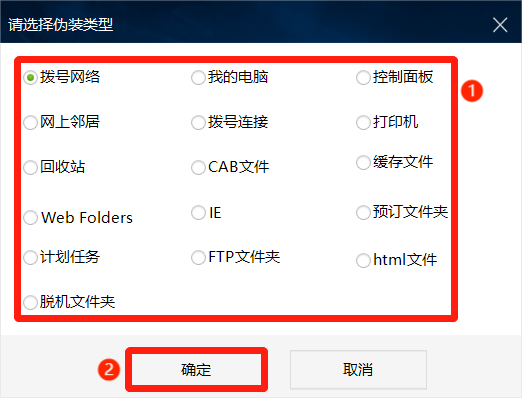
怎么防止重要文件夹丢失?文件夹安全如何保护?
我们在使用电脑的过程中,会将重要数据放在文件夹中,那么,我们该怎么防止重要文件夹丢失呢?下面我们就一起来了解一下。 EFS加密 EFS加密可以对于NTFS卷上的文件夹进行加密,加密后的文件夹将只允许加密时登录系统的用户…...

用于物体识别和跟踪的下游任务自监督学习-1-引言
一:引言: 图像和视频理解是计算机视觉应用中的基本问题,旨在使机器能够像人类一样解释和理解视觉数据。这些问题涉及识别图像和视频中的对象、人物、动作、事件和场景。如图1.1-(a)所示的图像识别任务包括对象检测[1]…...

式子表达ds类——多用位置/值域表示未知数+区间覆盖转区间加:CF407E
https://www.luogu.com.cn/problem/CF407E 多用位置/值域表示未知数 推出的式子中 n n n 表示长度,应该直接换成 r − l 1 r-l1 r−l1 区间覆盖转区间加 推出的式子有 m x , m n mx,mn mx,mn,朴素思路是用单调队列区间覆盖维护 那样就不能很方便…...
)
Python 实现秒表功能(比较好玩的题目)
以下实例使用 time 模块来实现秒表功能: import time print(按下回车开始计时,按下ctrlc停止计时) while True:input("")starttimetime.time()print(开始)try:while True:print(计时:,round(time.time()-starttime,0),秒)time.sle…...

DALL-E 3调参教程;百度新出的AI写小说神器;通义听悟看播客也太爽了;系列博文带你理解生成式AI | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🔥 2023年诺贝尔奖全部揭晓,一文看完6类奖项花落谁家 https://www.nobelprize.org/prizes 随着最后一项「经济学奖」的揭秘&a…...

设计模式-享元模式
概念 共享内存(主要考虑内存,而非效率)相同的数据,共享使用(JS中未找到经典应用场景) 演示 <!-- 无限下拉列表,将事件代理到高层节点上 --> <!-- 如果都绑定到<a>标签&#x…...

中秋时节赏明月,五子棋戏月饼趣 — Flutter中秋限定版五子棋
前言 当中秋时节来临,我们都期待着与亲人朋友共度这个美好的节日。这个时候,除了传统的赏月和品尝美味的月饼,我还有一个特别的建议——尝试一款有趣的Flutter五子棋游戏!这款五子棋游戏以中秋为主题,游戏的棋子也可爱…...
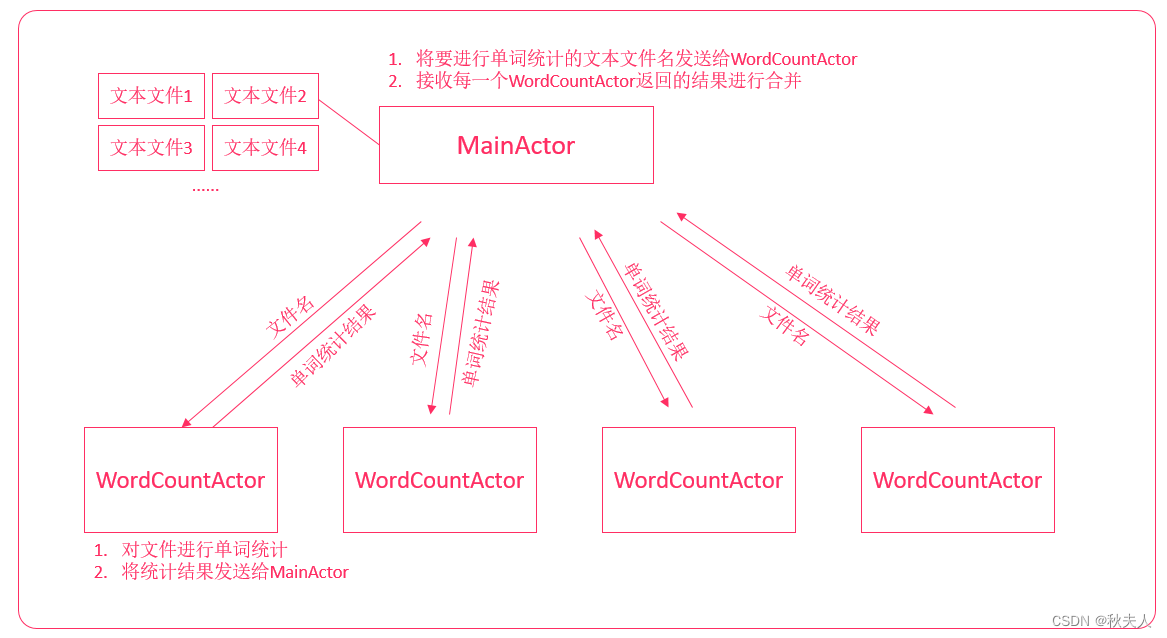
Scala第十九章节
Scala第十九章节 scala总目录 文档资料下载 章节目标 了解Actor的相关概述掌握Actor发送和接收消息掌握WordCount案例 1. Actor介绍 Scala中的Actor并发编程模型可以用来开发比Java线程效率更高的并发程序。我们学习Scala Actor的目的主要是为后续学习Akka做准备。 1.1 Ja…...

kafka与hbase的区别
Kafka 和 HBase 是两个不同的分布式数据存储系统,它们可以在大数据应用中发挥不同的作用。 Kafka 是一个高吞吐量的分布式发布订阅消息系统,主要用于处理实时数据流。它具有以下特点: 高性能:Kafka 能够以非常高的吞吐量和低延迟…...

出栈序列的合法性
给定一个最大容量为 M 的堆栈,将 N 个数字按 1, 2, 3, ..., N 的顺序入栈,允许按任何顺序出栈,则哪些数字序列是不可能得到的?例如给定 M5、N7,则我们有可能得到{ 1, 2, 3, 4, 5, 6, 7 },但不可能得到{ 3, …...
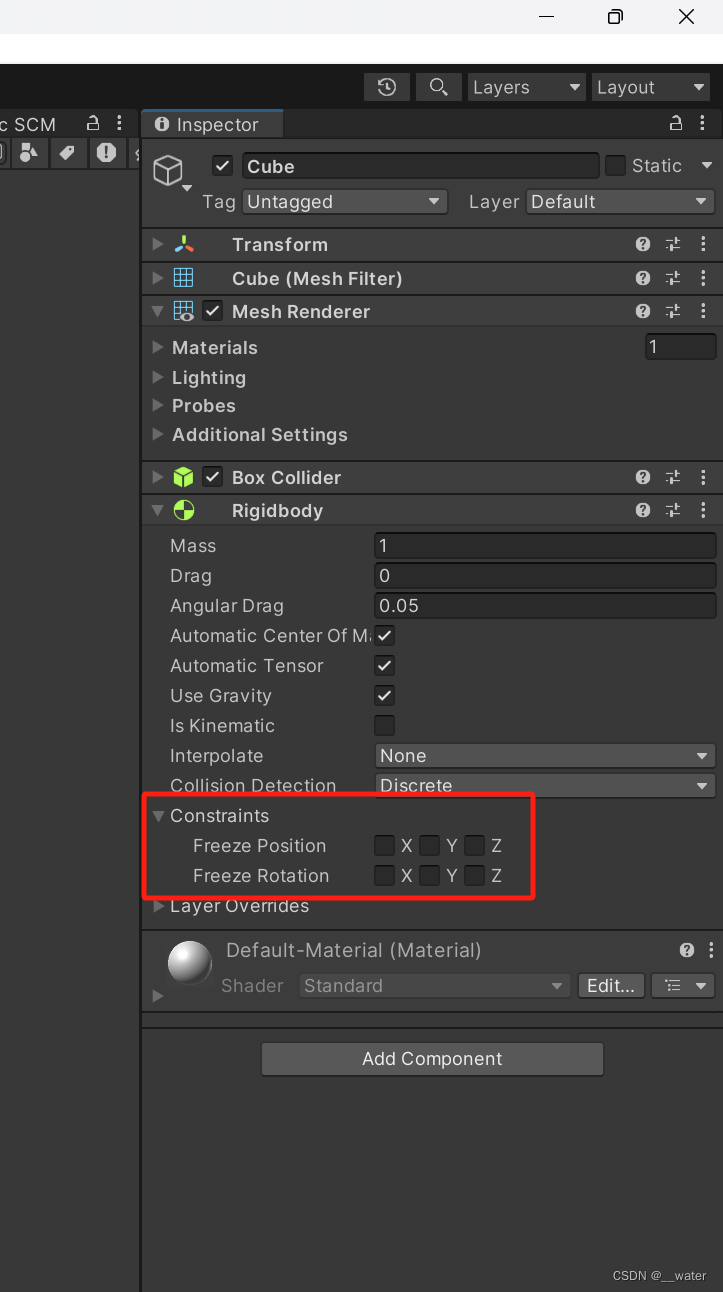
unity操作_刚体 c#
刚体Rigidbody 首先在场景中创建一个Plane 位置重置一下 再创建一个Cube 充值 y0.5 我们可以看出创建的Cube 和 Plane都自带碰撞器 Plane用的是网格碰撞器 我们可以通过网格世界看到不同的网格碰撞器 发生碰撞(条件): 两个物体都有碰撞器 …...
介绍(Python示例))
网络编程中套接字(socket)介绍(Python示例)
网络编程中套接字(socket)介绍(Python示例) 网络编程就是同一计算机的进程间或者不同的联网计算机之间的通信(交换数据)。 那么,这两台计算机之间用什么传输数据呢?首先你肯定先需要…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
