实现一个简单的线性回归和多项式回归(2)
对于多项式回归,可以同样使用前面线性回归中定义的LinearRegression算子、训练函数train、均方误差函数mean_squared_error,生成数据集create_toy_data,这里就不多做赘述咯~
拟合的函数为
def sin(x):y = torch.sin(2 * math.pi * x)return y
1.数据集的建立
func = sin
interval = (0,1)
train_num = 15
test_num = 10
noise = 0.5
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise = noise)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise = noise)X_underlying = torch.linspace(interval[0], interval[1], 100)
y_underlying = sin(X_underlying)# 绘制图像
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
#plt.scatter(X_test, y_test, facecolor="none", edgecolor="r", s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.legend(fontsize='x-large')
plt.savefig('ml-vis2.pdf')
plt.show()生成结果:
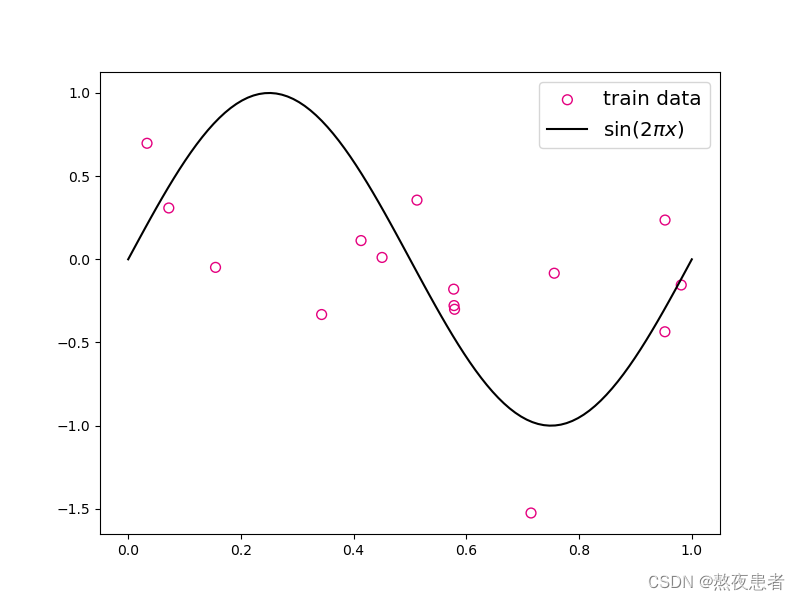
2.模型构建
# 多项式转换
def polynomial_basis_function(x, degree=2):"""输入:- x: tensor, 输入的数据,shape=[N,1]- degree: int, 多项式的阶数example Input: [[2], [3], [4]], degree=2example Output: [[2^1, 2^2], [3^1, 3^2], [4^1, 4^2]]注意:本案例中,在degree>=1时不生成全为1的一列数据;degree为0时生成形状与输入相同,全1的Tensor输出:- x_result: tensor"""if degree == 0:return torch.ones(x.size(), dtype=torch.float32)x_tmp = xx_result = x_tmpfor i in range(2, degree + 1):x_tmp = torch.multiply(x_tmp, x) # 逐元素相乘x_result = torch.concat((x_result, x_tmp), dim=-1)return x_result
我的理解多项式回归的模型的建立更像是将原来的一个x变成x x^2 x^3 ... x^degree这个过程
3.模型训练
plt.rcParams['figure.figsize'] = (12.0, 8.0)for i, degree in enumerate([0, 1, 3, 8]): # []中为多项式的阶数model = Linear(degree)X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), degree)X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), degree)model = optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1])) # 拟合得到参数y_underlying_pred = model(X_underlying_transformed).squeeze()print(model.params)# 绘制图像plt.subplot(2, 2, i + 1)plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")plt.plot(X_underlying, y_underlying_pred, c='#f19ec2', label="predicted function")plt.ylim(-2, 1.5)plt.annotate("M={}".format(degree), xy=(0.95, -1.4))# plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.legend(loc='lower left', fontsize='x-large')
plt.savefig('ml-vis3.pdf')
plt.show()
训练结果:
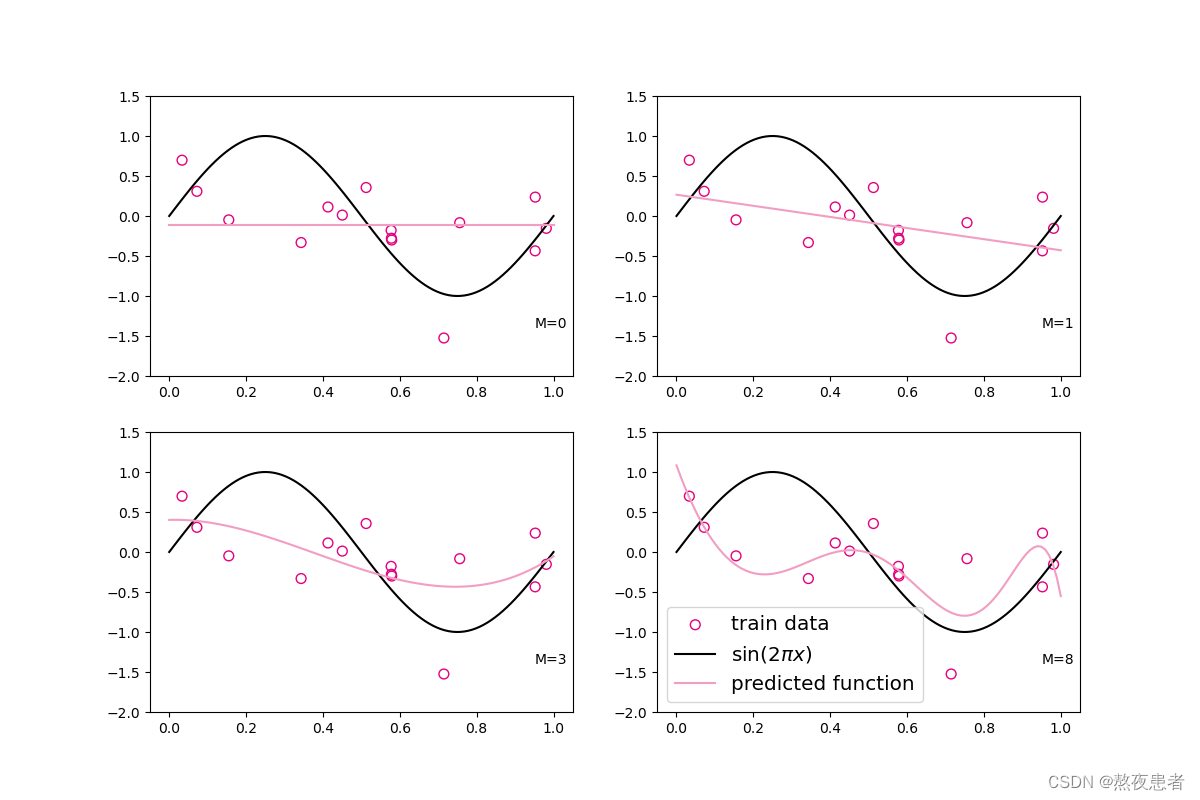
观察可视化结果,红色的曲线表示不同阶多项式分布拟合数据的结果:
* 当 或
时,拟合曲线较简单,模型欠拟合;
* 当 时,拟合曲线较复杂,模型过拟合;
* 当 时,模型拟合最为合理。
4.模型评估
下面通过均方误差来衡量训练误差、测试误差以及在没有噪音的加入下sin函数值与多项式回归值之间的误差,更加真实地反映拟合结果。多项式分布阶数从0到8进行遍历。
# 训练误差和测试误差
training_errors = []
test_errors = []
distribution_errors = []# 遍历多项式阶数
for i in range(9):model = Linear(i)X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), i)X_test_transformed = polynomial_basis_function(X_test.reshape([-1, 1]), i)X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), i)optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))y_train_pred = model(X_train_transformed).squeeze()y_test_pred = model(X_test_transformed).squeeze()y_underlying_pred = model(X_underlying_transformed).squeeze()train_mse = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()training_errors.append(train_mse)test_mse = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()test_errors.append(test_mse)# distribution_mse = mean_squared_error(y_true=y_underlying, y_pred=y_underlying_pred).item()# distribution_errors.append(distribution_mse)print("train errors: \n", training_errors)
print("test errors: \n", test_errors)
# print ("distribution errors: \n", distribution_errors)# 绘制图片
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.plot(training_errors, '-.', mfc="none", mec='#e4007f', ms=10, c='#e4007f', label="Training")
plt.plot(test_errors, '--', mfc="none", mec='#f19ec2', ms=10, c='#f19ec2', label="Test")
# plt.plot(distribution_errors, '-', mfc="none", mec="#3D3D3F", ms=10, c="#3D3D3F", label="Distribution")
plt.legend(fontsize='x-large')
plt.xlabel("degree")
plt.ylabel("MSE")
plt.savefig('ml-mse-error.pdf')
plt.show()可视化结果如下:
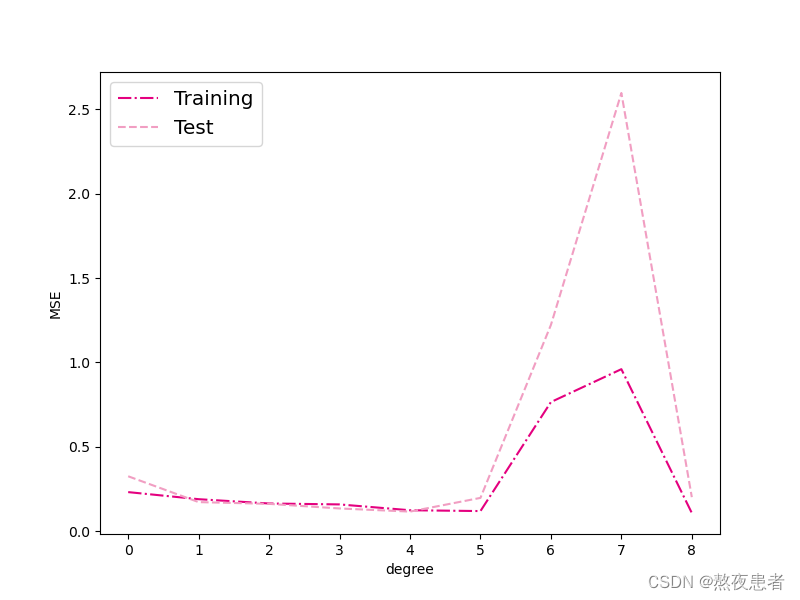
由可视化结果可得:
- 当阶数较低的时候,模型的表示能力有限,训练误差和测试误差都很高,代表模型欠拟合;
- 当阶数较高的时候,模型表示能力强,但将训练数据中的噪声也作为特征进行学习,一般情况下训练误差继续降低而测试误差显著升高,代表模型过拟合。
对于模型过拟合的情况,可以引入正则化方法,通过向误差函数中添加一个惩罚项来避免系数倾向于较大的取值。
degree = 8 # 多项式阶数
reg_lambda = 0.0001 # 正则化系数X_train_transformed = polynomial_basis_function(X_train.reshape([-1,1]), degree)
X_test_transformed = polynomial_basis_function(X_test.reshape([-1,1]), degree)
X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1,1]), degree)model = Linear(degree) optimizer_lsm(model,X_train_transformed,y_train.reshape([-1,1]))y_test_pred=model(X_test_transformed).squeeze()
y_underlying_pred=model(X_underlying_transformed).squeeze()model_reg = Linear(degree) optimizer_lsm(model_reg,X_train_transformed,y_train.reshape([-1,1]),reg_lambda=reg_lambda)y_test_pred_reg=model_reg(X_test_transformed).squeeze()
y_underlying_pred_reg=model_reg(X_underlying_transformed).squeeze()mse = mean_squared_error(y_true = y_test, y_pred = y_test_pred).item()
print("mse:",mse)
mes_reg = mean_squared_error(y_true = y_test, y_pred = y_test_pred_reg).item()
print("mse_with_l2_reg:",mes_reg)# 绘制图像
plt.scatter(X_train, y_train, facecolor="none", edgecolor="#e4007f", s=50, label="train data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.plot(X_underlying, y_underlying_pred, c='#e4007f', linestyle="--", label="$deg. = 8$")
plt.plot(X_underlying, y_underlying_pred_reg, c='#f19ec2', linestyle="-.", label="$deg. = 8, \ell_2 reg$")
plt.ylim(-1.5, 1.5)
plt.annotate("lambda={}".format(reg_lambda), xy=(0.82, -1.4))
plt.legend(fontsize='large')
plt.savefig('ml-vis4.pdf')
plt.show()可视化结果为:
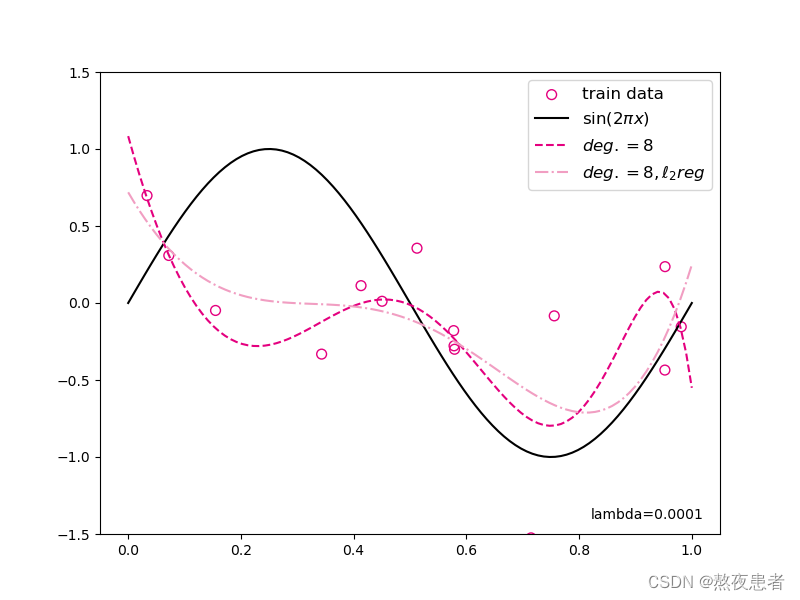
多项式回归的难点就是是否真正理解了线性回归中的算子,均方误差等函数的目的和用法,其他的就是简单的函数调用问题啦~不懂的话还是建议多看看线性函数,先把线性函数的看明白最好~
相关文章:

实现一个简单的线性回归和多项式回归(2)
对于多项式回归,可以同样使用前面线性回归中定义的LinearRegression算子、训练函数train、均方误差函数mean_squared_error,生成数据集create_toy_data,这里就不多做赘述咯~ 拟合的函数为 def sin(x):y torch.sin(2 * math.pi * x)return y1.数据集的建…...

云原生Kubernetes:K8S集群kubectl命令汇总
目录 一、理论 1.概念 2. kubectl 帮助方法 3.kubectl 子命令使用分类 4.使用kubectl 命令的必要环境 5.kubectl 详细命令 一、理论 1.概念 kubectl是一个命令行工具,通过跟 K8S 集群的 API Server 通信,来执行集群的管理工作。 kubectl命令是操…...

Java使用模板导出word、pdf
使用deepoove根据模板导出word文档,包括文本、表格、图表、图片,使用WordConvertPdf可将word文档转换为pdf导出 模板样例: 导出结果: 一、引入相关依赖 <!-- 工具类--><dependency><groupId>cn.hutool&…...

速通Redis基础(二):掌握Redis的哈希类型和命令
目录 Redis 哈希类型简介 Redis 哈希命令 HSET HGET HEXISTS HDEL HKEYS HVALS HGETALL HMGET HLEN HSETNX 编辑 HINCRBY HINCRBYFLOAT Redis的哈希类型命令小结 Redis 是一种高性能的键值存储数据库,支持多种数据类型,其中之…...

WebDAV之π-Disk派盘 + 书藏家
书藏家是一款书籍收藏的软件,对于喜欢阅读书籍的用户来说非常友好,记录你所阅读的书籍内容,对你所阅读的书籍内容进行全方位的管理,并且支持多种录入的方式,不管是实体书籍还是网络书籍都能够进行更为有效的管理;内置WebDAV 模块,更加便利的整理自己的文件资源;书藏家的…...

香港Web3.0生态现状
目前香港Web3.0生态正在快速发展。香港政府和金融机构正在积极推动Web3.0生态的建设,以推动数字经济和智慧城市的发展。香港政府已经发布了有关虚拟资产发展的政策宣言,鼓励和监管并重,加大力度推动虚拟资产产业向前发展。同时,香…...
)
LLMs之BELLE:源码解读(sft_train.py文件)
LLMs之BELLE:源码解读(sft_train.py文件) 目录 源码解读(sft_train.py文件) # 1、解析命令行参数,包括模型参数、数据参数和训练参数。...
【UE5 Cesium】17-Cesium for Unreal 建立飞行跟踪器(2)
目录 效果 步骤 一、飞机沿航线飞行 二、通过切换相机实现在不同角度观察飞机飞行 效果 步骤 一、飞机沿航线飞行 先去模型网站下载一个波音737飞机模型 然后将下载好的模型导入到UE项目中,导入时需要勾选“合并网格体”(导入前最好在建模软件中将…...
【ElasticSearch】基于 Java 客户端 RestClient 实现对 ElasticSearch 索引库、文档的增删改查操作,以及文档的批量导入
文章目录 前言一、对 Java RestClient 的认识1.1 什么是 RestClient1.2 RestClient 核心类:RestHighLevelClient 二、使用 Java RestClient 操作索引库2.1 根据数据库表编写创建 ES 索引的 DSL 语句2.2 初始化 Java RestClient2.2.1 在 Spring Boot 项目中引入 Rest…...

【Node.js】stream 流模块
流是一种抽象的数据结构。从键盘输入到应用程序就是标准输入流(stdin)。应用程序把字符一个一个输出到显示器上叫做:标准输出流(stdout)。 流的特点是数据是有序的,而且必须依次读取,或者依次写…...
【LeetCode】——链式二叉树经典OJ题详解
主页点击直达:个人主页 我的小仓库:代码仓库 C语言偷着笑:C语言专栏 数据结构挨打小记:初阶数据结构专栏 Linux被操作记:Linux专栏 LeetCode刷题掉发记:LeetCode刷题 算法头疼记:算法专栏…...

代码注释对于程序员重要吗?
程序员对代码注释可以说是又爱又恨又双标……你是怎么看待程序员不写注释这一事件的呢? 代码注释的重要性 代码注释是指在程序代码中添加的解释性说明,用于描述代码的功能、目的、使用方法等。代码注释对于程序的重要性主要体现在以下几个方面&#x…...

OpenHamony开发笔记一:在HarmonyOS虚拟机上运行openharmony工程
在HarmonyOS的虚拟机上要运行openharmony的工程时需要修改的地方有 1.修改build-profile.json5,将runtimeOS改为HarmonyOS "targets": [{"name": "default","runtimeOS": "HarmonyOS"}, 2.修改工程引用的SDK&a…...
)
C++程序员入门需要怎么学?(InsCode AI 创作助手)
文章目录 (一)学习C概念(二)C主要应用场景和相关产品(三)学习C流程1. 学习C语法和基本示例:2. 深入学习面向对象编程(OOP):3. 使用C标准库:4. 解决…...
)
Intel 高性能库之IPP信号处理简介及下载(版本5.1,含32位和64位及注册)
IPP是什么 IPP:Intel Integrated Performance Primitives 英特尔集成性能基元(英特尔IPP)是一款多核就绪的扩展函数库,其中包含众多针对多媒体、数据处理和通信应用高度优化的软件函数。它包括: 视频编码:用于 DV25/50/100、MPEG-2、MPEG-4、H.263 和 MPEG-4 Part 10 …...
【C++】运算符重载案例 - 字符串类 ② ( 重载 等号 = 运算符 | 重载 数组下标 [] 操作符 | 完整代码示例 )
文章目录 一、重载 等号 运算符1、等号 运算符 与 拷贝构造函数2、重载 等号 运算符 - 右操作数为 String 对象3、不同的右操作数对应的 重载运算符函数 二、重载 下标 [] 运算符三、完整代码示例1、String.h 类头文件2、String.cpp 类实现3、Test.cpp 测试类4、执行结果 一…...

Vue脚手架开发流程
一、项目运行时会先执行 public / index.html 文件 <!DOCTYPE html> <html lang""><head><meta charset"utf-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport&quo…...

从零开始学习线性回归:理论、实践与PyTorch实现
文章目录 🥦介绍🥦基本知识🥦代码实现🥦完整代码🥦总结 🥦介绍 线性回归是统计学和机器学习中最简单而强大的算法之一,用于建模和预测连续性数值输出与输入特征之间的关系。本博客将深入探讨线性…...

[LeetCode]链式二叉树相关题目(c语言实现)
文章目录 LeetCode965. 单值二叉树LeetCode100. 相同的树LeetCode101. 对称二叉树LeetCode144. 二叉树的前序遍历LeetCode94. 二叉树的中序遍历LeetCode145. 二叉树的后序遍历LeetCode572. 另一棵树的子树 LeetCode965. 单值二叉树 题目 Oj链接 思路 一棵树的所有值都是一个…...
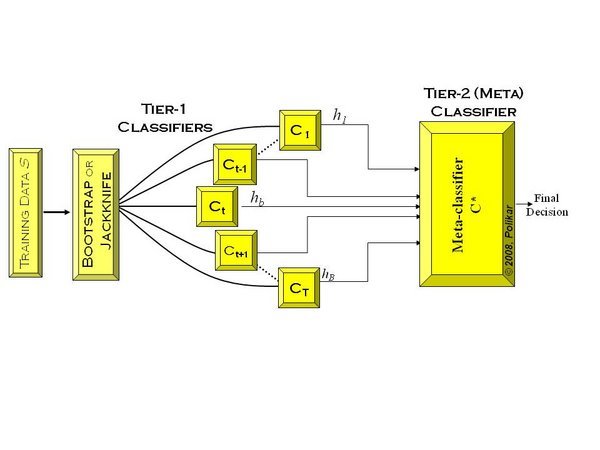
集成学习
集成学习(Ensemble Learning) - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/27689464集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型,集成学习潜在的思想是即便某一个弱分类器得到了错误的预测,其他的弱分类器…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
