Redis-持久化机制
持久化机制介绍
- RDB
- AOF
- RDB和AOF对比
RDB
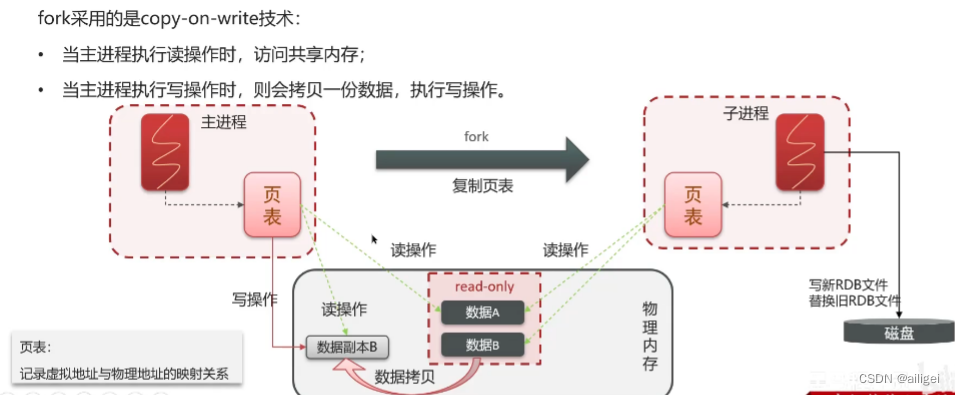
rdb的话是利用了写时复制技术，他是看时间间隔内key值的变化量，就比如20秒内如果有5个key改变过的话他就会创建一个fork子进程（bgsave），通过这个子进程，将数据快照进入一个临时文件，完成之后再将临时文件去覆盖dump.rdb文件
主要流程如下：
AOF
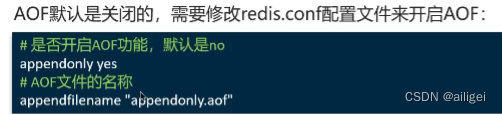
AOF:Redis 默认不开启。它的出现是为了弥补RDB的不足（数据的不一致性），所以它采用日志的形式来记录每个写操作，并追加到文件中（秒级）
AOF的命令记录的频率也可以通过redis.conf文件来配置，一般我们是采用everysec
因为是记录命令，AOF文件会比RDB文件大很多，而且AOF会记录对同一个key的多次写操作，但是实际上只有最后一次才有意义。
我们可以通过bgrewriteaof命令，让AOF文件执行重写功能，这样他就可以只记录最后一次，减少命令的行数
当然，其实redis中也会在触发阈值的时候自动去重写AOF文件，阈值也可以在redis.conf中配置，
RDB和AOF对比
RDB和AOF各自有各自的优点，如果我们需要对数据的安全性要求高的话，在实际开发中会结合两者来一起使用
相关文章：
Redis-持久化机制
持久化机制介绍 RDBAOFRDB和AOF对比 RDB rdb的话是利用了写时复制技术，他是看时间间隔内key值的变化量，就比如20秒内如果有5个key改变过的话他就会创建一个fork子进程（bgsave），通过这个子进程，将数据快照进…...
【LeetCode热题100】--155.最小栈
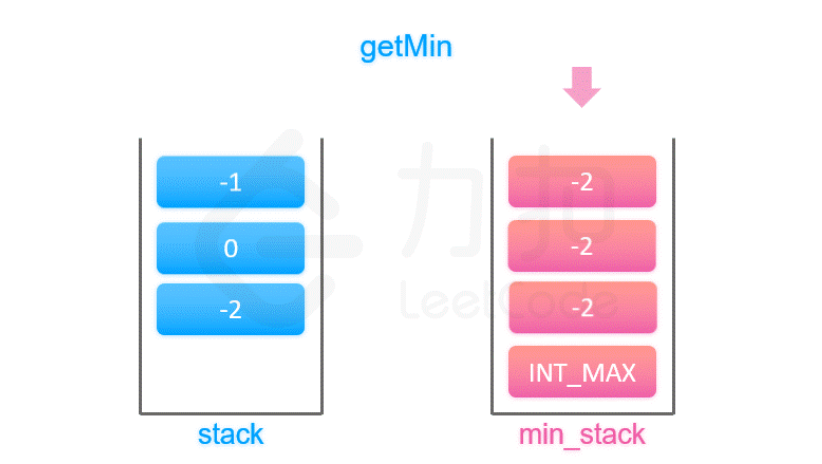
155.最小栈 设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元…...
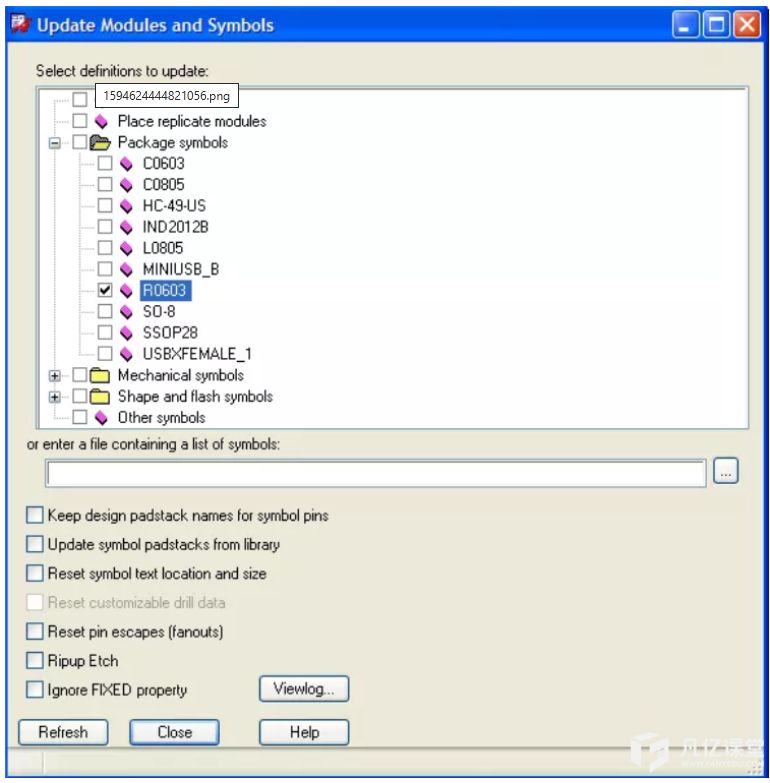
Allegro 17.2如何直接更新元件封装？
想必很多从事电子设计的小伙伴，都有这样的经历：有些时候原理图和PCB设计是由不同的工程师负责，然后偶尔需要在没有原理图的情况下直接对PCB作品进行操作，如更新元件封装等操作，这种环节不仅费时费力，效率贼…...
高效数据管理：Java助力实现Excel数据验证
摘要：本文由葡萄城技术团队原创并首发。转载请注明出处：葡萄城官网，葡萄城为开发者提供专业的开发工具、解决方案和服务，赋能开发者。 前言 在Java中，开发者可以使用一些开源的库（如Apache POI）…...
Easysearch Chart 0.2.0都有哪些变化
Easysearch Chart 包更新了，让我们来看看都有哪些变化： Docker 镜像升级 Service 名称调整，支持 NodePort 模式部署 现在让我们用 NodePort 模式部署一下： # helm search repo infinilabs NAME CHART VERSION …...
RV1126-RV1109-进入uboot的按键和名字显示-HOSTNAME
今天添加一个小功能,就是uboot是按CTRLC进入的 今日我做了一个定制,让按L或者l让也进入uboot指令模式,并且修改主板名字显示 默认是CTRLC:键码值是0x03(ASCII对照表) 于是代码中跟踪: //rv1126_rv1109/u-boot/common/console.c int ctrlc(void) { #ifndef CONFIG_SANDBOXif (…...
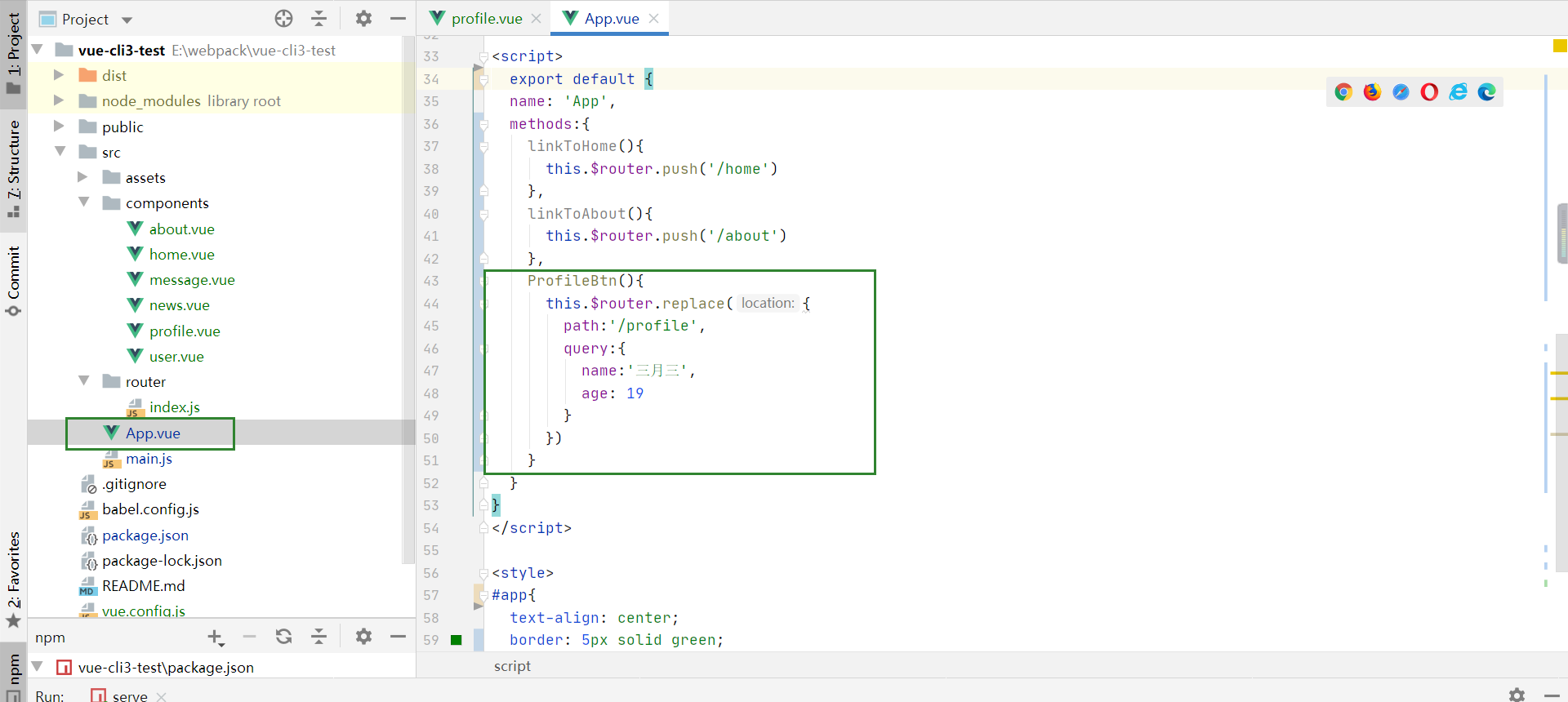
学习vue-router
可参见: vue-router 详解_vue router_七月J的博客-CSDN博客 https://www.cnblogs.com/chen-ao666/p/17144552.html vue-router的使用 使用vue-router的步骤: 创建路由组件 配置路由映射: 组件和路径映射关系 使用路由: 通过和 <router-link>: 该标签是一个vue-router中…...
Python爬虫提高排名
在如今竞争激烈的互联网时代，网站的SEO优化变得尤为重要。而Python爬虫作为一种强大的工具，可以帮助网站主们提升搜索排名，吸引更多的流量和用户。本文将为您揭秘如何利用Python爬虫来改善您的SEO优化，并帮助您提升搜索排名。无论…...
SQL获取正数第N个或倒数第N个数据
这里我们使用Order By与Limit的组合： Order By：可以将某个序列值按照从大到小或从小到大排序Limit：如果类似Limit 5表示前5个，Limit 3,5表示从第4个位置（以0为开始）开始往后取5个 通过这样的组合就可以实…...
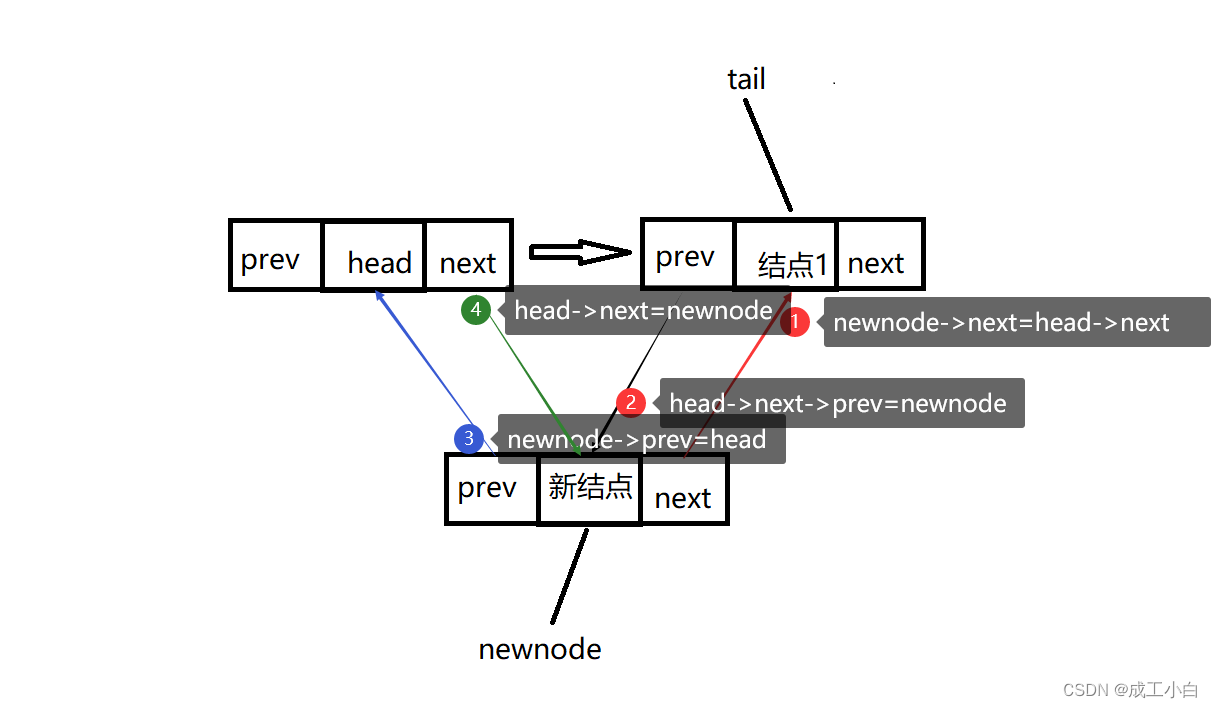
链表（2）——带头双向循环链表
🍁一、链表的分类 🌕1.单向或者双向 🌕2.带头或者不带头（有无哨兵） 🌕3.循环或者不循环 🌕4.无头单向非循环链表（常用） 🌕5.带头双向循环链表（常用…...
C语言 函数指针
函数指针是C语言中的一种特殊类型，它允许你像操作变量一样操作函数。函数指针的主要用途是存储并后续调用一组函数。 在C语言中，函数指针的定义通常如下所示： 返回类型 (*指针变量名)(参数类型) 例如，如果你有一个返回整数并接受…...
F. Vasilije Loves Number Theory
Problem - F - Codeforces 思路：分析一下题意，对于第一种操作来说，每次乘以x，那么nn*x，然后问是否存在一个a使得gcd(n,a)1并且n*a的约数个数等于n，有最大公约数等于1我们能够知道其实这两个数是互质的&…...
electron打包后主进程下载文件崩溃
electronvue3写了一个小项目，实现了一个文件下载功能 存在的问题 打包后，应用下载文件崩溃代码 // 渲染进程window.electron.ipcRenderer.invoke(save-file, {path: r.filePath,fileurl: previewUrl,}).then(response > {console.log(response ----…...
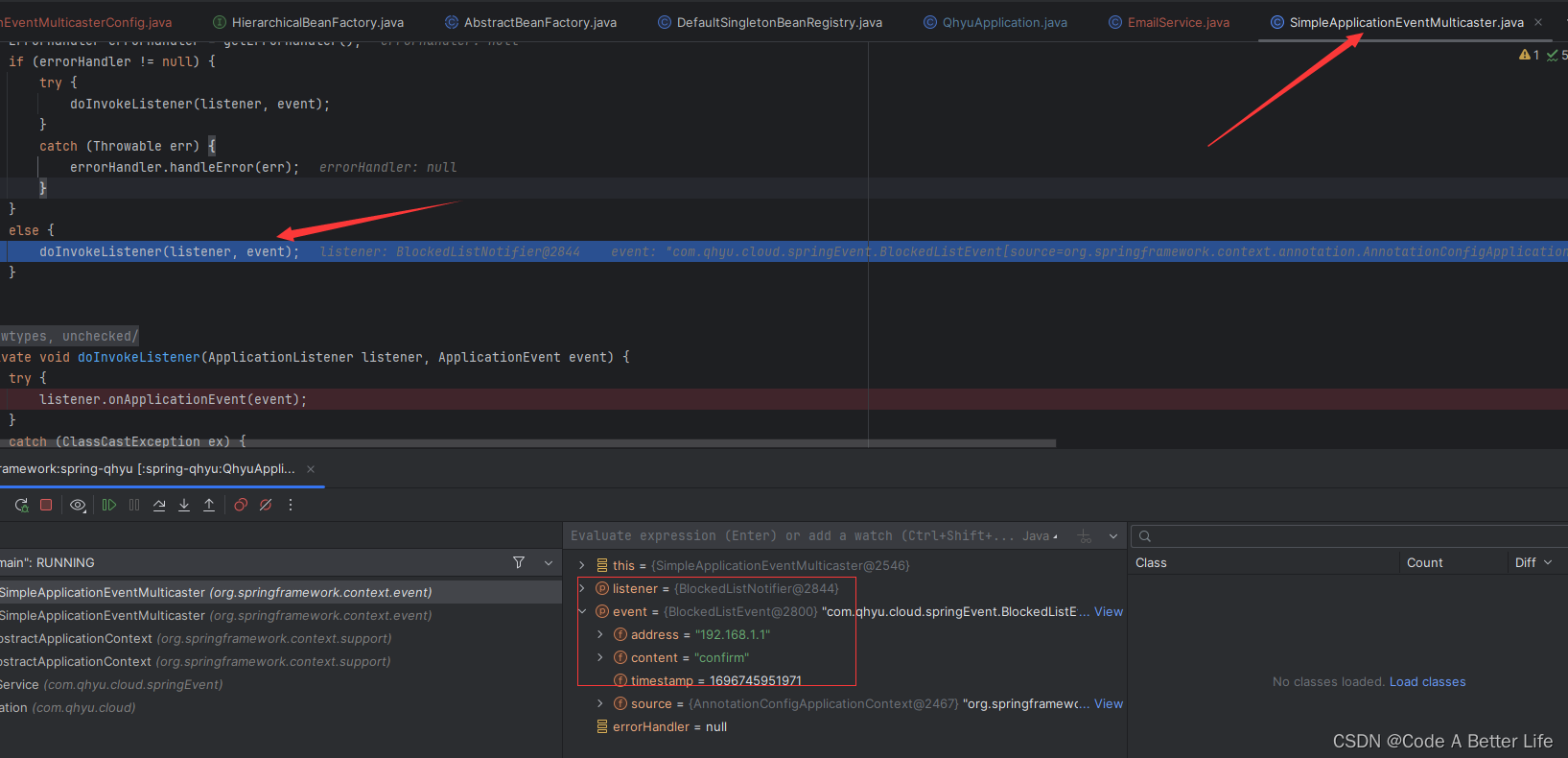
Spring实例化源码解析之Custom Events下集(九)
上集从官网的角度讲解了基本的使用和源码的内容，没有深入的进行分析，本章将从源码的角度分析ApplicationEvent、ApplicationListener、ApplicationEventMulticaster这三者之间的关系。 initApplicationEventMulticaster 上一章后续部分给出了源码的含义…...
python numpy库关键函数说明
python numpy库函数说明 np.argwhere()np.dtype()np.shape()np.zeros() np.argwhere() 输入参数是一个基本的逻辑表达式，输出检索结果的索引值。 >>> x np.arange(6).reshape(2,3) >>> x array([[0, 1, 2],[3, 4, 5]]) >>> np.argwhe…...
【Linux C】Linux如何执行一个程序（程序存储空间、系统调用、内核调用）
文章目录 一、程序存储空间1.1 C语言程序存储空间1.2 用户空间和内核空间1.3 用户模式和内核模式 二、内核调用-系统调用-C语言库函数2.1 系统调用和内核调用2.2 C语言库函数 三、Linux如何执行一个程序 一、程序存储空间 本节说的空间主要是指内存空间，即程序如何分…...
IP协议总结
一、定义。 IP全称为Internet Protocol，是TCP/IP协议族中的一员，负责实现数据在网络上的传输。它是一种无连接、不可靠的数据报协议。 IP协议常用于Internet网络和局域网中，它通过将数据包进行分组并进行逐跳转发来实现数据在网络中的传输。…...
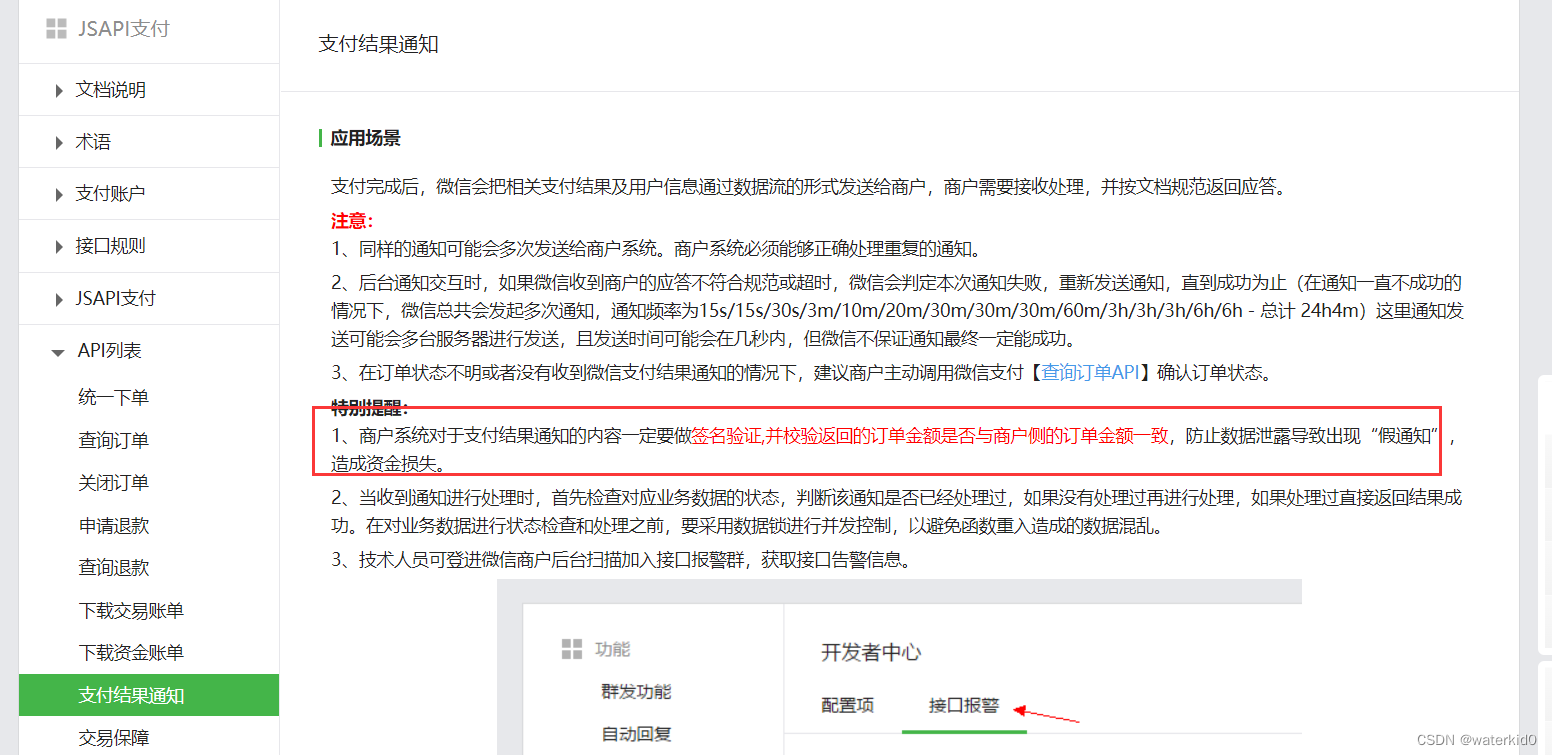
微信支付v2
文档： https://pay.weixin.qq.com/wiki/doc/api/index.html 微信小程序：https://pay.weixin.qq.com/wiki/doc/api/jsapi.php?chapter11_1 需要一个微信认证后的小程序，，还需要一个，在微信商户平台，&…...
tcpdump(二)命令行参数讲解(一)
一 tcpdump实战详解 1、我们做抓包,一般都需要指定条件,保证对系统的CPU、内存、磁盘资源不会产生过大的响应备注： 遇到过tcpdump持续抓包导致系统挂了2、条件：1) tcpdump的 基础命令选项参数2) 真正的 过滤条件 抓包工具tcpdump用法说明 ① 参数学…...
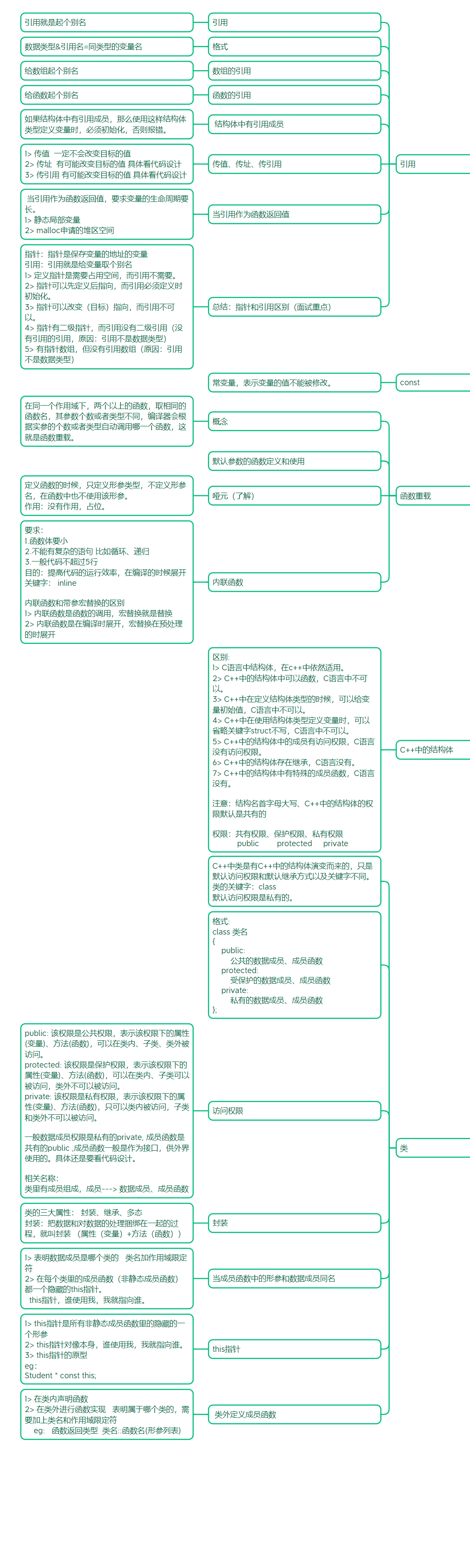
10_8C++
X-Mind #include <iostream>using namespace std; class Rect { private:int width;int heigjt; public:void init(int w,int h){width w;heigjt h;}void set_w(int w){width w;}void set_h(int h){heigjt h;}void show(){cout << "矩形的周长" <…...
conda相比python好处
Conda 作为 Python 的环境和包管理工具，相比原生 Python 生态（如 pip 虚拟环境）有许多独特优势，尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处： 一、一站式环境管理：…...
iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘
美国西海岸的夏天，再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至，这不仅是开发者的盛宴，更是全球数亿苹果用户翘首以盼的科技春晚。今年，苹果依旧为我们带来了全家桶式的系统更新，包括 iOS 26、iPadOS 26…...
IGP（Interior Gateway Protocol，内部网关协议）
IGP（Interior Gateway Protocol，内部网关协议） 是一种用于在一个自治系统（AS）内部传递路由信息的路由协议，主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目（父项目）主要用于依赖管理 一些需要注意的点： 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件，否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
SpringTask-03.入门案例
一.入门案例 启动类： package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系，以下是深入解析： 门铃FIFO溢出的本质 在RapidIO系统中，门铃消息FIFO是硬件控制器内部的缓冲区，用于临时存储接收到的门铃消息（Doorbell Message）。…...
MySQL账号权限管理指南：安全创建账户与精细授权技巧
在MySQL数据库管理中，合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号？ 最小权限原则…...
[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机，点进去 点进去 查看URL，有 ?fileflag.php说明存在文件包含，原理是php://filter 协议 当它与包含函数结合时，php://filter流会被当作php文件执行。 用php://filter加编码，能让PHP把文件内容…...
pgsql：还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题： pgsql数据库通过备份数据库文件进行还原时，如果表中有自增序列，还原后可能会出现重复的序列，此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”，…...