【数据结构】算法的时间复杂度
🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

目录
一.算法时间复杂度定义
二.大O阶渐近表示法
🎏大O阶渐近表示法的定义
🎏推导大O阶方法
三.常见的时间复杂度
📌常数阶
📌线性阶
📌对数阶
📌平方阶
📌调用函数的时间复杂度
📌常见的时间复杂度及其耗时排序
四.最坏情况与平均情况
结语
一.算法时间复杂度定义
上一小节我们讲到,比较两个算法的优劣最重要的比较方式就是拿算法的时间复杂度来做比较.这节我们就来系统的学习一下算法的时间复杂度:
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间.
一个算法所花费的时间与其中语句的总执行次数T(n)成正比例,算法中的基本操作的执行次数,为算法的时间复杂度.
二.大O阶渐近表示法
🎏大O阶渐近表示法的定义
一般情况下,算法中基本操作重复执行的次数T(n)是问题规模n的某个函数f(n),
算法的时间量度记作
T(n)=O(f(n))
它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称做算法的渐近时间复杂度,简称时间复杂度.
这样用大写O( )来体现算法时间复杂度的记法,我们称之为大O记法.
大O符号(Big O notation):是用于描述函数渐近行为的数学符号.
一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法.
🎏推导大O阶方法
1.用常数1取代运行时间中的所有加法常数.
2.在修改后的运行次数函数中,只保留最高阶项.
3.如果最高阶项存在且不是1,则去除与这个项目相乘的常数.
经过上面这三步简单的操作后,得到的结果就是大O阶.
三.常见的时间复杂度
📌常数阶
我们首先来看顺序结构的时间复杂度.
如下算法,我们将一起分析上篇文章提到过的高斯算法为什么时间复杂度不是O(4),而是O(1).
int sum=0; /*执行一次*/
int n; /*执行一次*/
sum=(1+n)*n/2; /*执行一次*/
printf("%d",sum); /*执行一次*/显而易见,这个算法的运行次数函数是f(n)=4.
根据我们推导大O阶的方法,第一步就是把常数项4改为1.在保留最高项时发现,它根本没有最高阶项,所以这个算法的时间复杂度为O(1).
接下来,我们试想一下,如果这个算法当中的语句"sum=(1+n)*n/2"有10句,即:
int sum = 0; /*执行第1次*/int n ; /*执行第1次*/sum = (1 + n) * n / 2; /*执行第1次*/sum = (1 + n) * n / 2; /*执行第2次*/sum = (1 + n) * n / 2; /*执行第3次*/sum = (1 + n) * n / 2; /*执行第4次*/sum = (1 + n) * n / 2; /*执行第5次*/sum = (1 + n) * n / 2; /*执行第6次*/sum = (1 + n) * n / 2; /*执行第7次*/sum = (1 + n) * n / 2; /*执行第8次*/sum = (1 + n) * n / 2; /*执行第9次*/sum = (1 + n) * n / 2; /*执行第10次*/printf("%d", sum); /*执行第1次*/事实上,无论n为多少,上面的两段代码就是3次和13次执行的差异.
这种与问题的大小无关(n的多少),执行时间恒定的算法,我们称之为具有O(1)的时间复杂度,又叫常数阶.
注意:不管这个常数是多少,我们都记作O(1),而不是O(4),O(13)等其他任何数字,这是初学者常常犯的错误.
另外,对于分支结构而言(如:if...else...,switch...case)等,无论是真还是假,执行的次数都是恒定的,不会随着n的变大而发生变化.
所以单纯的分支结构(不包含在循环结构中),其时间复杂度也是O(1).
📌线性阶
线性阶的循环结构会复杂很多.要确定某个算法的阶次,我们常常需要确定某个特定语句或某个语句集运行的次数.因此,我们要分析算法的复杂度,关键就是要分析循环结构的运行情况.
如下面这段代码,它的总执行次数为2n+2次,按照推导大O阶方法,去掉最高项系数,去掉非最高项的项,我们得到该代码的时间复杂度为O(n).
要注意的是,对线性阶来讲,它最高项前的系数即便是999999999,我们在推导大O阶时也要将它去掉,只要它的系数是一个常数,那它的大O阶就是O(n).
int i = 0; /*执行一次*/int n ; /*执行一次*/for (i = 0; i < 2 * n; i++){/*时间复杂度为O(1)的程序步骤序列*/ /*执行2*n次*/}📌对数阶
再来看下面这段代码:
int count = 1; /*执行一次*/int n ; /*执行一次*/while (count < n){count = count * 2; /*执行"logn"次*/}由于每次count乘以2之后,就距离n更近了一分.count与多少个2相乘后大于n就会退出循环.
设循环内基本操作的循环次数为x,可得2^x=n,即.
因此这个循环的时间复杂度为O(logn).
(tips:在数据结构中,时间复杂度如果为,因为在计算机上不好表示这个函数,因此常常为了方便会简写为:logn.但这种简写仅限于以2为底的对数,其他的对数都不能用这种简写.)
📌平方阶
下面的例子是一个我们熟悉的二维数组:
int arr[10][10] = { 0 }; /*执行一次*/int i = 0; /*执行一次*/int j = 0; /*执行一次*/int n ; /*执行一次*/for (i = 0; i < n; i++){for (j = 0; j < n; j++){arr[i][j] = i + j; /*执行n*n次*/}}这段代码的总执行次数为n^2+4次,按照大O阶推导方法,去掉常数项,得到这段代码的时间复杂度为O(n^2).
这个例子中,如果外循环的循环次数改为了m,时间复杂度就变成O(m*n):
int arr[10][10] = { 0 }; /*执行一次*/int i = 0; /*执行一次*/int j = 0; /*执行一次*/int n ; /*执行一次*/int m ; /*执行一次*/for (i = 0; i < m; i++){for (j = 0; j < n; j++){arr[i][j] = i + j; /*执行m*n次*/}}所以我们可得,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数.
再来看看下面这个循环嵌套的时间复杂度:
int arr[10][10] = { 0 }; /*执行一次*/int i = 0; /*执行一次*/int j = 0; /*执行一次*/int n = 10; /*执行一次*/for (i = 0; i < n; i++){for (j = i; j < n; j++){arr[i][j] = i + j; /*执行?次*/}}这个程序循环执行的总次数可能不太好看出来,不过我们可以列个表计算一下:
| i的值 | 内循环执行的次数 |
|---|---|
| i=0 | n |
| i=1 | n-1 |
| i=2 | n-2 |
| ... | ... |
| i=n-2 | 2 |
| i=n-1 | 1 |
将i从0到n-1的每个内循环执行的次数加起来可得总的执行次数为:n+(n-1)+(n-2)+...+2+1=n*(n+1)/2=n^2/2+n/2.
根据大O阶推导方法可得,这段代码的时间复杂度为O(n^2).
📌调用函数的时间复杂度
再看下面这个例子:
int i = 0; /*执行一次*/int j = 0; /*执行一次*/int n; /*执行一次*/for (i = 0; i < n; i++){function(i); /*执行n次*/}上面这段代码中的for循环调用一个函数function:
void function(int count)
{printf("%d",count); /*执行一次*/
}因为function函数的时间复杂度是O(1).所以整体的时间复杂度为O(1)*O(n)=O(n).
而假如function是这样的:
void function(int count)
{int j;for (j = 0; j < n;j++){/*时间复杂度为O(1)的程序步骤序列*/}
}很明显,这种情况下,function函数的时间复杂度是O(n).
所以整体的时间复杂度为O(n)*O(n)=O(n^2).
最后再看一个相对复杂的语句:
n++; /*执行一次*/
function(n); /*执行n次*/
int i; /*执行一次*/
int j; /*执行一次*/
for (i = 0; i < n:i++) /*执行n^2次*/
{function(i);
}
for (i = 0; i < n; i++) /* 执行n(n+1)/2次 */
{for (j = i; j < n; j++){/*时间复杂度为O(1)的程序步骤序列*/}
}
function和上面一样:
void function(int count)
{int j;for (j = 0; j < n;j++){/*时间复杂度为O(1)的程序步骤序列*/}
}可得,这个程序的执行次数T(n)=1+n+1+1+n^2+(n^2)/2+n/2=,根据推导大O阶的方法去掉系数和非最高阶项,最终这段代码的时间复杂度仍然是O(n^2).
📌常见的时间复杂度及其耗时排序
| 执行次数函数 | 阶 | 非正式术语 |
|---|---|---|
| 14 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n^2+2n+1 | O(n^2) | 平方阶 |
| O(logn) | 对数阶 | |
| O(nlogn) | nlogn阶 | |
| 6n^3+2n^2+3n+4 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
常用的时间复杂度所耗费的时间从小到大依次是:
四.最坏情况与平均情况
我们先来分析一个我们熟悉的程序哈,冒泡排序程序:
void bubbleSort(int arr[], int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){// 交换arr[j]和arr[j+1]int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}int main()
{int arr[] = { 64, 34, 25, 12, 22, 11, 90 };int n = sizeof(arr) / sizeof(arr[0]);bubbleSort(arr, n);printf("排序后的数组:\n");for (int i = 0; i < n; i++){printf("%d ", arr[i]);}return 0;
}冒泡排序逻辑图示如下:

我们假设我们要排序的数组是{9,8,7,6,5,4,3,2,1,0},而我们的目标是将它们排成升序,即{0,1,2,3,4,5,6,7,8,9}.
计算一下这种情况下程序的运行次数(因为交换元素的三步操作的时间复杂度是O(1),所以我们将它们视为执行1次):9+8+7+6+5+4+3+2+1=45次.
由此易得出,当数组元素个数为n时,冒泡排序的执行次数函数T(n)=n*(n+1)/2.
你有没有发现一个问题,如果冒泡排序的待排序数组是{9,8,7,6,5,4,3,2,1,0},而我们的目标排序数组是{0,1,2,3,4,5,6,7,8,9},那简直是太"倒霉了",就像你为了参加公司组团夏天去夏威夷旅游买了好多短袖,短裤,墨镜,泳衣等装备,而最后公司却决定冬天去哈尔滨旅游一样.其实这种情况就是程序运行时间的最坏情况.
相应的,程序运行时间也会有最好情况,最好情况就是,冒泡排序的待排序数组是{9,8,7,6,5,4,3,2,1,0},而我们的目标数组也是{9,8,7,6,5,4,3,2,1,0},那程序运行的次数就是0次,这就是程序运行时间的最好情况.
但现实生活中,我们大部分遇到的数据都没有这么极端,根据正态分布原则,反而是只需要排最坏次数一半的次数出现的可能性大一些.我们将这种情况称为平均时间复杂度.
平均时间是所有情况中最有意义的,因为他是期望的运行时间.
对算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法称为平均时间复杂度.
另一种方法是计算最坏情况下的时间复杂度,这种方法称为最坏时间复杂度.
知道了这两种方法之后,我们还需要做一件事,就是要考虑在实际运用中到底选择这两个哪个复杂度作为衡量算法好坏的时间复杂度.
其实,在应用中,除非特殊指定,我们提到的运行时间都是最坏情况的运行时间.
因为最坏情况运行时间是一种保证,那就是运行时间将不会再坏了.
不好理解的话,我举个例子:
假如你和女朋友约好今天下午在图书馆约会,你估计自己大概1-3点之间能到达约会的目的地,这时候你的女朋友问你约会时间定在几点,你会和她说1点还是2点还是3点?
如果定在一点,那你有2/3的概率会迟到,如果定在2点,那你还是有1/3的概率会迟到,一旦迟到,就将给女孩子留下很不好的印象.
所以我们最好还是将时间定在3点,因为这是一种保证,就是再迟,也不会比三点还迟了.

对算法运行时间的估量也是这个道理,再加上在很多情况下,各种输入数据集出现的概率难以确定,算法的平均时间复杂度也就难以计算.
因此在实际中一般情况我们关注的是算法的最坏运行情况.
结语
当我们搞清楚什么是算法的时间复杂度后,在数据结构算法篇,我们还将一起学习算法的空间复杂度及算法效率的度量方法相关的知识.希望这些内容能对大家有所帮助,一起学习,一起进步!
相关文章推荐
【数据结构】什么是数据结构?
【数据结构】什么是算法?【数据结构】算法效率的度量方法
【数据结构】算法的空间复杂度
【C语言】冒泡排序
......

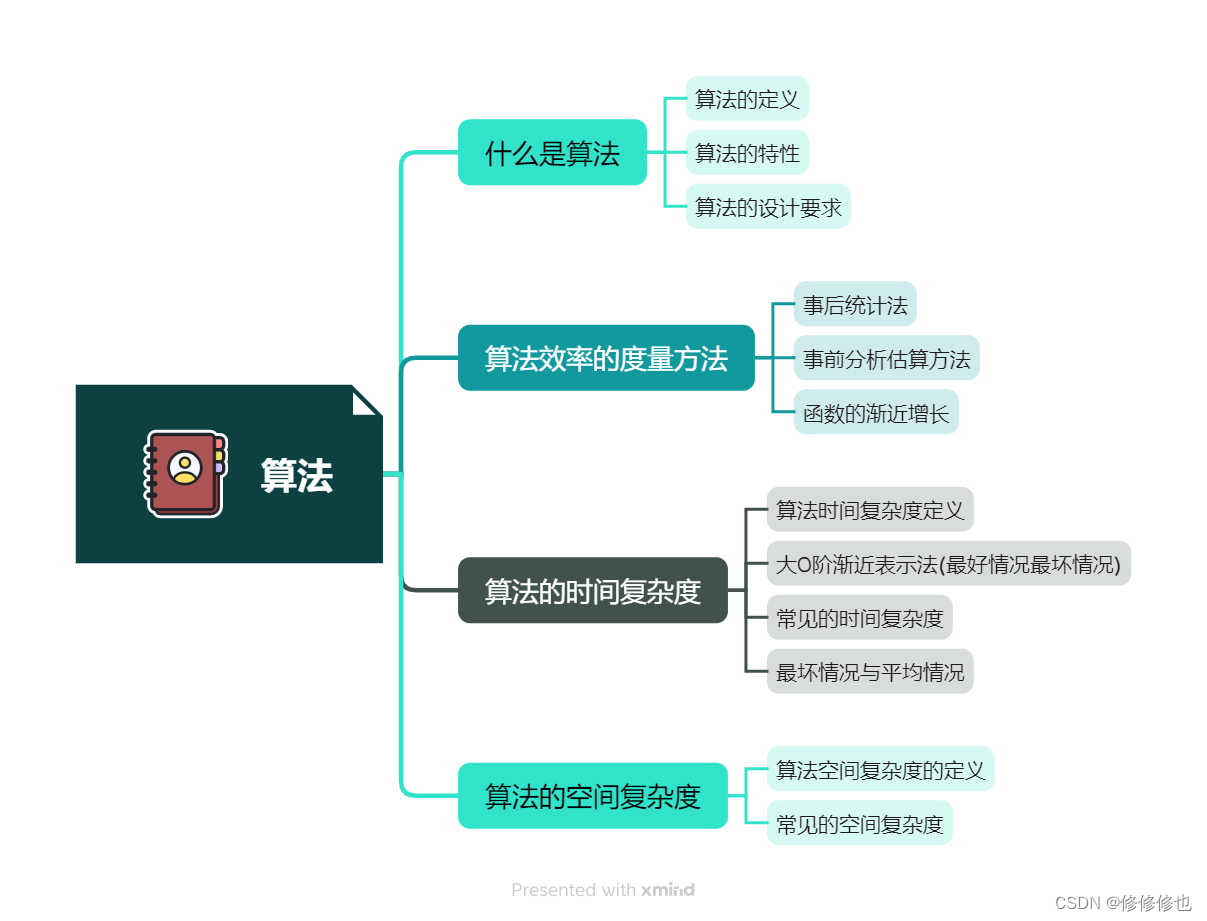
数据结构算法篇思维导图:
相关文章:

【数据结构】算法的时间复杂度
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 一.算法时间复杂度定义 二.大O阶渐近表示法 🎏大O阶渐近表示法的定义 🎏推导大O阶方法 三.常见的时间复杂度 📌常数阶 &#x…...

Qt作业五
1、思维导图 https://www.zhixi.com/view/9e899ee0 2、作业 #include <iostream>using namespace std;class Animal { private:string name; public:Animal(){}Animal(string n):name(n){}virtual void perform()0; };class Lion:public Animal { public:void perform…...

【面试】pc寄存器题
目录 1.使用pc寄存器存储字节码指令地址有什么作用?(为什么使用pc寄存器记录当前线程的执行地址?)2.pc寄存器为什么被设定为线程私有的? 1.使用pc寄存器存储字节码指令地址有什么作用?(为什么使…...
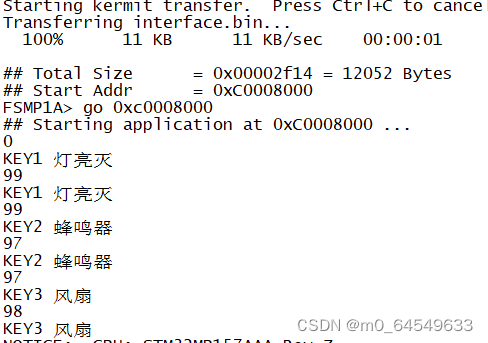
ARM按键中断实验
设置按键中断,按键1按下,LED亮,再按一次,灭 按键2按下,蜂鸣器响。再按一次,不响 按键3按下,风扇转,再按一次,风扇停 src/do_irq.c #include "key_it.h" ex…...

C#的值类型和引用类型
不得不说c#的类型系统设计有点意思,不同的编程语言对于类型的设计各有取舍。 值类型: 当我们将一个int类型的值赋值到另一个int类型的值时,它实际上是创建了一个完全不同的副本。换句话说,如果你改变了其中某一个的值࿰…...

YOLOv7改进:极简的神经网络模型 VanillaNet---VanillaBlock助力检测,实现暴力涨点 | 华为诺亚2023
💡💡💡本文属于原创独家改进:极简模块VanillaBlock,以极简主义的设计为理念,网络中仅仅包含最简单的卷积计算,去掉了残差和注意力模块,二次创新引入到YOLOv7中取得了不俗的效果。 极简模块VanillaBlock | 亲测在多个数据集实现涨点; 收录: YOLOv7高阶自研专…...

对验证码的识别爆破
声明:该系列文章首发于公众号:Y1X1n安全,转载请注明出处!本公众号所分享内容仅用于每一个爱好者之间的技术讨论及教育目的,所有渗透及工具的使用都需获取授权,禁止用于违法途径,否则需自行承担&…...
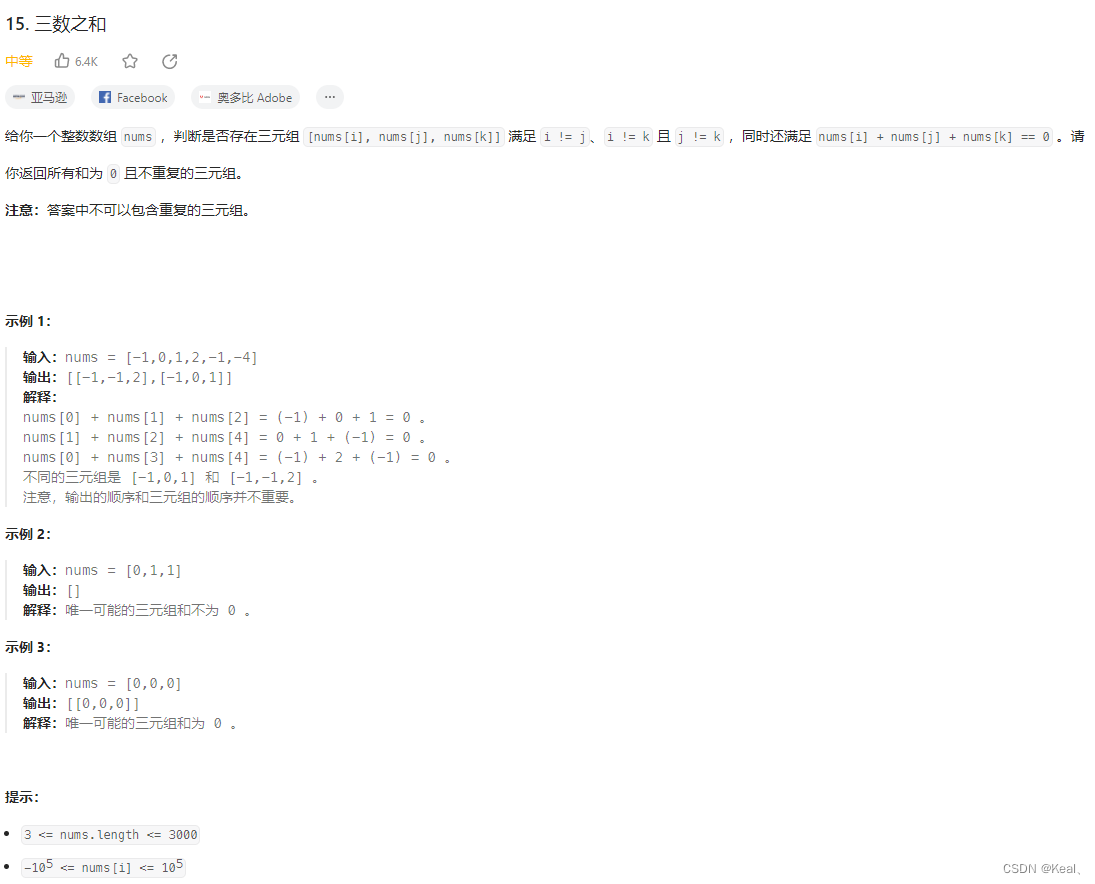
LeetCode【15】三数之和
题目: 解析: 参考:https://zhuanlan.zhihu.com/p/111715985 代码: public static List<List<Integer>> threeSum(int[] nums) {// 先排序Arrays.sort(nums);List<List<Integer>> result new ArrayLis…...

Gossip协议是什么
Gossip协议是什么 Gossip protocol 也叫 Epidemic Protocol (流行病协议), 是基于流行病传播方式的节点或者进程之间信息交换的协议, 也被叫做流言算法, 八卦算法、疫情传播算法等等. 说到 Gossip 协议, 就不得不提著名的六度分隔理论. 简单地说, 你和任何一个陌生人之间所间…...
)
【java学习】this关键字(27)
文章目录 1. this是什么?2. this的作用 1. this是什么? 在 java 中,this关键字比较难理解,它的作用和其词义很接近。 ①它在方法内部使用,即这个方法所属对象的引用; ②它在构造器内部使用,表示…...

27、元组
区分: 数组:纯粹 一个[]中的数据类型都是一致的 元组:不纯粹 一个[]中可能有不同类型的数据项 意义 当赋值或访问一个已知索引的元素时,可以得到正确的类型 let miao: [string, number] [cat, 18]; miao[0] cat miao[1] 18…...
--数据处理)
1km分辨率逐月降雨量和最高温度数据集(1901-2022)--数据处理
1km分辨率逐月降雨量和最高温度数据集(1901-2022)的下载可以参考我的另外一篇博客: 这里的温度和降雨数据集都是NC格式的,需要将其处理为tif格式,我采用的处理软件是MATLAB。 本篇博客以处理温度数据为例,…...

docker入门加实战—docker常见命令
docker入门加实战—docker常见命令 在介绍命令之前,先用一副图形象的展示一下docker的命令: 常见命令 docker的常见命令和文档地址如下表: 命令说明文档地址docker pull拉取镜像docker pulldocker push推送镜像到DockerRegistrydocker pus…...

【C/C++】使用 g++ 编译器编译 C++ 程序的完全指南
本文介绍了 g 编译器的使用方法和常见参数解释,帮助您编译和构建 C 程序。 引言 在 C 程序开发中,选择一个合适的编译器是至关重要的。g 是 GNU 编译器集合(GCC)中的 C 编译器,提供了丰富的功能和选项,帮…...

ARM中断实验
设置按键中断,按键1按下,LED亮,再按一次,灭 按键2按下,蜂鸣器响。再按一次,不响 按键3按下,风扇转,再按一次,风扇停 main.c #include "uart1.h" #include …...
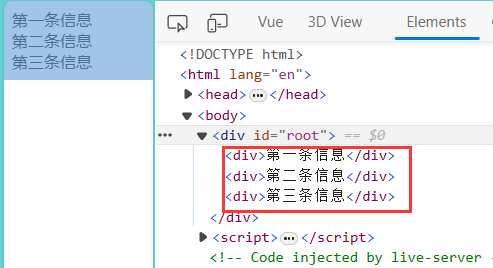
Vue条件渲染
一、使用v-show条件渲染 语法格式: v-show"表达式" // true 或 false 当表达式的值为true的时候就显示,表达式值为false的时候隐藏。 下面是使用v-show实现的一个点击按钮切换显示和隐藏的小案例 : 值得注意的是,使…...

k8s中如何使用gpu、gpu资源讲解、nvidia gpu驱动安装
前言 环境:centos7.9、k8s 1.22.17、docker-ce-20.10.9 gpu资源也是服务器中常见的一种资源,gpu即显卡,一般用在人工智能、图文识别、大模型等领域,其中nvidia gpu是nvidia公司生产的nvidia类型的显卡,amd gpu则是adm…...
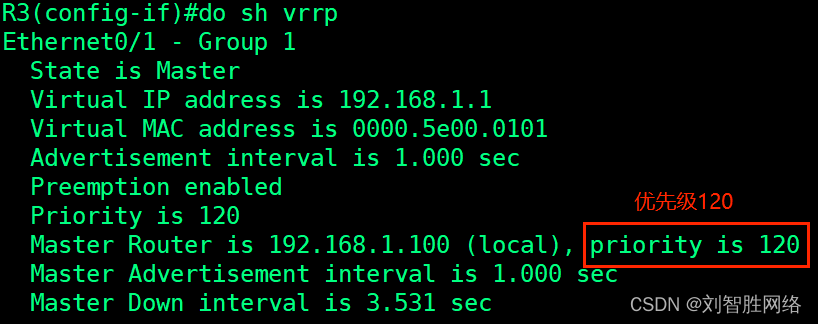
VRRP 虚拟路由器冗余协议的解析和配置
VRRP的解析 个人简介 原理和HSRP的差不多,少了一些状态就只有了三种状态 还有不同的就是VRRP严格按照抢占要求 一个VRRP组中具有最高优先级的设备成为Master路由器缺省优先级为100若优先级相同,具有最高接口IP地址最大的路由器成为Master路由器抢占(Pr…...
旅游网站HTML
代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>旅游网</title> </head> <body><!--采用table编辑--> <!--最晚曾table,用于整个页面那布局--><table width&q…...
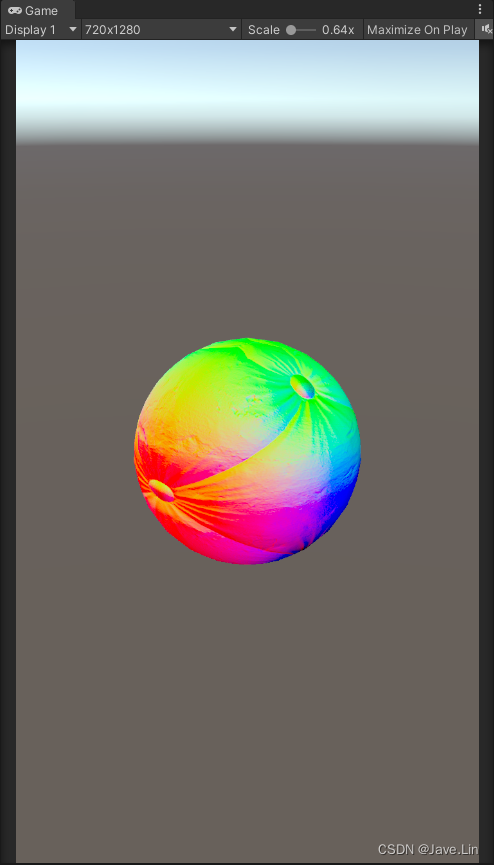
Unity - Normal mapping - Reoriented normal mapping - 重定向法线、混合法线
文章目录 目的核心代码PBR - Filament - Normal mappingShader效果BlendNormal_Hill12BlendNormal_UDNBlendNormals_Unity_Native - 效果目前最好 ProjectReferences 目的 备份、拾遗 核心代码 half3 blended_normal normalize(half3(n1.xy n2.xy, n1.z*n2.z));PBR - Filam…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
