【数据结构】二叉树--顺序结构及实现 (堆)
目录
一 二叉树的顺序结构
二 堆的概念及结构
三 堆的实现
1 包含所有接口 (Heap.h)
2 初始化,销毁和交换(Heap.c)
3 向上调整(Heap.c)
4 插入(Heap.c)
5 向下调整(Heap.c)
6 删除(Heap.c)
7 打印(Heap.c)
8 返回堆顶(Heap.c)
9 判断是否为空(Heap.c)
10 测试(Test.c)
一 二叉树的顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空 间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺 序存储在物理上是一个数组,在逻辑上是一颗二叉树。

二 堆的概念及结构
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1, 2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质: 堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
三 堆的实现
1 包含所有接口 (Heap.h)
#pragma once
#include<stdbool.h>
#include<assert.h>
#include<stdlib.h>
#include<stdio.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;//向上调整
void AdjustUp(HPDataType* a, int child);//向下调整
void AdjustDown(HPDataType* a, int n, int parent);//交换
void Swap(HPDataType* p1, HPDataType* p2);
//打印
void HeapPrint(HP* php);
//初始化
void HeapInit(HP* php);
//销毁
void HeapDestroy(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//返回堆顶
HPDataType HeapTop(HP* php);
//是否为空
bool HeapEmpty(HP* php);2 初始化,销毁和交换(Heap.c)
#include"Heap.h"void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}//交换
void Swap(HPDataType* p1, HPDataType* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}3 向上调整(Heap.c)
时间复杂度 O(logN)
//向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent])//如果建大堆 就改成 a[child] > a[parent]{Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

4 插入(Heap.c)
//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = (php->capacity == 0 ? 4 : php->capacity * 2);HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
} 5 向下调整(Heap.c)
5 向下调整(Heap.c)
时间复杂度 O(logN)
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//找小的那个孩子if (child+1 < n && a[child+1] < a[child])//child+1<n 防止数据越界 如果想改成大堆 改成>{child++;}if (a[child] < a[parent])//如果想大堆 改成>{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
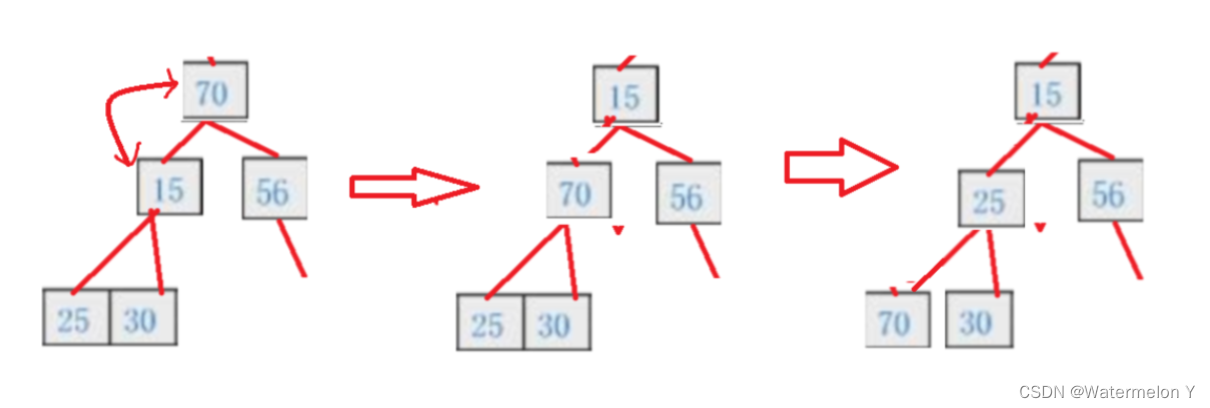
6 删除(Heap.c)
//删除
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
} 7 打印(Heap.c)
7 打印(Heap.c)
//打印
void HeapPrint(HP* php)
{assert(php);for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}8 返回堆顶(Heap.c)
//返回堆顶
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}9 判断是否为空(Heap.c)
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}//堆为空返回1 true
//堆不为空 返回0 false10 测试(Test.c)
小堆情况(升序)
#include"Heap.h"int main()
{int a[] = { 2,3,5,7,4,6,8,65,100,70,32,50,60 };HP hp;HeapInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}HeapPrint(&hp);while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}HeapDestroy(&hp);return 0;
}
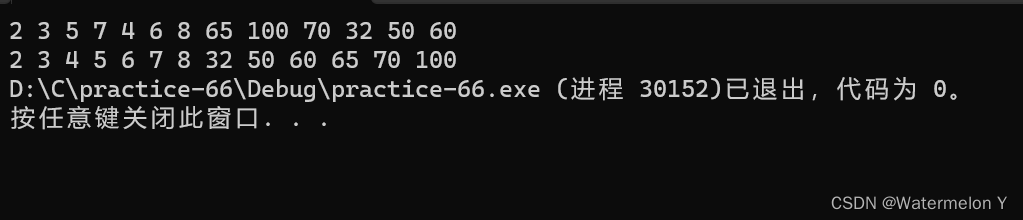
但是这种排序方式有明显的缺陷
1、先有一个堆的数据结构
2、空间复杂度复杂度的消耗
所以我们可以改进一下 用真正的堆排序 堆排序有很多细节 所以放在后面一节讲
本节很基础 与栈的实现有很多相似之处 大家也可以看我之前对栈的讲解 以此加深印象
继续加油!
相关文章:

【数据结构】二叉树--顺序结构及实现 (堆)
目录 一 二叉树的顺序结构 二 堆的概念及结构 三 堆的实现 1 包含所有接口 (Heap.h) 2 初始化,销毁和交换(Heap.c) 3 向上调整(Heap.c) 4 插入(Heap.c) 5 向下调整(Heap.c) 6 删除(Heap.c) 7 打印&#…...

适用于嵌入式单片机的差分升级通用库
转至:痞子衡嵌入式半月刊:第 81 期 1、mcu_bsdiff_upgrade - 适用于嵌入式单片机的差分升级通用库 mcu_bsdiff_upgrade 是一款适用于嵌入式单片机的差分升级库,通用所有单片机,如stm32、华大、复旦微、瑞萨等。适合嵌入式的差分升…...
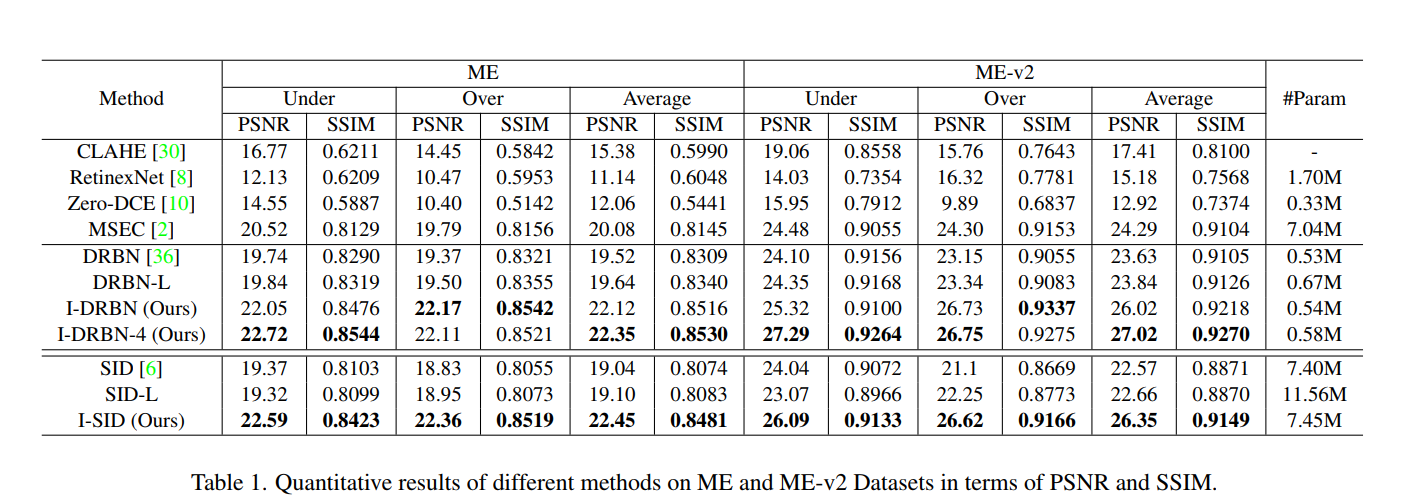
Exposure Normalization and Compensation for Multiple-Exposure Correction 论文阅读笔记
这是CVPR2022的一篇曝光校正的文章,是中科大的。一作作者按同样的思路(现有方法加一个自己设计的即插即用模块以提高性能的思路)在CVPR2023也发了一篇文章,名字是Learning Sample Relationship for Exposure Correction。 文章的…...
)
Arduino驱动BMI160 6轴惯性运动传感器(惯性测量传感器篇)
目录 1、传感器特性 2、硬件原理图 3、控制器和传感器连线图 4、驱动程序...

数据挖掘实战(3):如何对比特币走势进行预测?
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

巴以冲突中暴露的摄像头正对安全构成威胁
巴以冲突爆发后,许多配置不当的安全摄像头正暴露给黑客活动分子,使其周遭人员面临巨大安全风险。 Cybernews 研究人员发现,在以色列至少有165 个暴露的联网 RTSP 摄像头,在巴勒斯坦有 29 个暴露的 RTSP 摄像头。在巴勒斯坦&am…...

【Redis】Redis性能优化:理解与使用Redis Pipeline
原创不易,注重版权。转载请注明原作者和原文链接 文章目录 Pipeline介绍原生批命令(MSET, MGET) VS PipelinePipeline的优缺点一些疑问Pipeline代码实现 当我们谈论Redis数据处理和存储的优化方法时,「 Redis Pipeline」无疑是一个不能忽视的重要技术。…...
)
前端全局工具函数utils.js/正则(持续更新)
1. 接口返回提示 // 接口返回提示requestCodeTips(code, msg) {// code错误码,msg提示信息let errorrMessage switch (Number(code)) {case 400:errorrMessage 错误请求break;case 401:errorrMessage 未授权,请重新登录break;case 403:errorrMessage 拒绝访问b…...
如何基于先进视频技术,构建互联网视频监控安全管理平台解决方案
一、建设思路 依托互联网,建设一朵云,实现各类二三类视频资源统一接入,实现天网最后100米、10米、1米的全域覆盖。 依托人工智能与互联网技术,拓展视频资源在政府、社会面等多领域的全面应用;建设与运营模式并存&…...

【React native】navigation 状态重置
reset The reset action allows to reset the navigation state to the given state. It takes the following arguments: 重置操作允许将导航状态重置为给定状态: navigation.reset({index: 1,routes: [{name: Home}],});参考链接: 官方文档 https://reactnavigat…...
2023全国大学生软件测试大赛开发者测试练习题99分答案(ScapegoatTree2023)
2023全国大学生软件测试大赛开发者测试练习题99分答案(ScapegoatTree2023) 题目详情题解代码(直接全部复制到test类中即可)提示:该题只需要分支覆盖得分即可,不需要变异得分 题目详情 题解代码(直接全部复制到test类中即可) package net.mooctest;import static org.…...

Centos8 openjdk升级
1、卸载旧版本 sudo dnf remove java-1.8.0-openjdk 2、搜索新版本 yum search java-11-openjdk3、安装新版本 dnf install java-11-openjdk.x86_644、验证新版本 java -version...

开启深度学习之门—《深度学习》
开启深度学习之门—《深度学习》 《深度学习》由Ian Goodfellow和Yoshua Bengio合著,以其前沿的内容和深入浅出的风格,成为了当今最受欢迎的人工智能教材之一。首先,让我们来了解一下这两位作者。Ian Goodfellow是一位备受瞩目的计算机科学家…...

优先调节阀位,条件调节阀位
控制对象的执行机构可能存在多个,举例,压力通过变频和翻板这两个执行机构调节。默认调节翻板。这里定义一个全局布尔变量 bfgflag 初始默认为0;优先调节翻板,当翻板处于极限阀位时,bfgflag 赋值为1,开始调节…...

oracle入门笔记六
一、索引(index) 1、索引的作用 索引是优化查询的一种,使得查询效率特别高,索引是优化存储,索引作用在字段上 2、什么样的字段适合建索引 a、经常被查询的字段 b、不能为空,不能重复 c、字段的值不会被经常…...

腾讯云优惠券种类、领取方法及使用教程分享
腾讯云是国内领先的云计算服务提供商,为用户提供丰富的云计算产品和服务。为了吸引更多用户使用腾讯云的产品和服务,腾讯云会定期推出各种优惠券活动。本文将为大家介绍腾讯云优惠券的种类、领取方法及使用教程。 一、腾讯云优惠券种类介绍 腾讯云优惠券…...
JavaScript使用类-模态窗口
**上节课我们为这个项目获取了一些DOM元素,现在我们可以继续;**这个模态窗口有一个hidden类,这个类上文我们讲了,他的display为none;如果我们去除这个hidden的话,就可以让这个模态窗口展现出来。如下 cons…...

【轻松玩转MacOS】外部设备篇
引言 在开始之前,我们先来了解一下为什么要连接外部设备。想象一下,你正在享受MacOS带来的便捷和高效,突然需要打印一份文件,但你发现打印机无法连接;或者你需要将手机投屏到电脑上,却不知道该如何操作。这…...

location rewrite
Nginx location 匹配的规则和优先级 Nginx常用的变量 rewrite: 重定向功能 Location 匹配 URI URI:统一资源的表示符,是一种字符串标识,用于标识抽象或者物理资源 先来巩固一些与location结合使用的正则表达式 正则表达式:匹…...
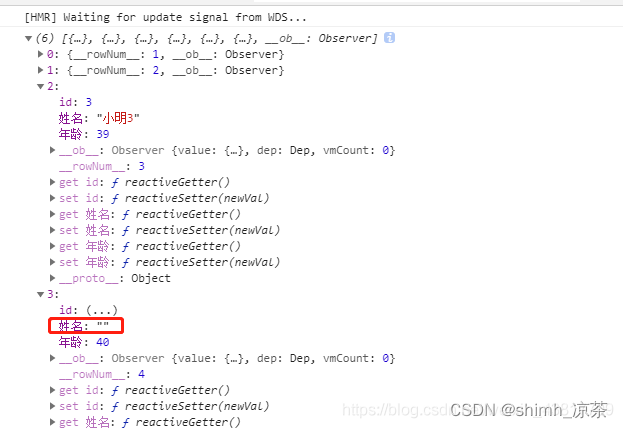
XLSX.utils.sheet_to_json()解析excel,给空的单元格赋值为空字符串
前言 今天用到XLSX来解析excel文件,调用XLSX.utils.sheet_to_json(worksheet),发现如果单元格为空的话,解析出来的结果,就会缺少相应的key(如图所示)。但是我想要单元格为空的话,值就默认给空字…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

