【考研408常用数据结构】C/C++实现代码汇总
文章目录
- 前言
- 数组
- 多维数组的原理、作用
- 稀疏数组
- 链表
- 单向链表的增删改查的具体实现思路
- 约瑟夫环问题(可不学)
- 双向链表
- 树
- 二叉搜索树
- 中序线索二叉树
- 哈夫曼树的编码与译码
- 红黑树
- B树
- B+树
- 堆
- 顺序与链式结构队列实现
- 优先队列排序算法(重点)
- 栈
- 顺序存储结构与链式存储结构栈
- 单调栈算法(可不学)
- 图
- 邻接矩阵与邻接表的深度优先遍历
前言
Github代码仓库地址
这一篇文章是因为有几个玩的比较好的朋友觉得我DS学的还行,然后他们也要准备考研了(有24也有25的),就希望我出一篇讲DS的文章,所以就有了这篇文章。
(毕竟现在的互联网好像是不论是小中大厂好像都喜欢问算法哈哈哈,也算给自己复习一下)
其实掌握这些数据结构最快速的方法就是先了解基础,自己动手实现一边,然后分析这些结构可以用在什么场景下。
然后基于他们的特性去刷题。
比如我做树的题的时候,一定最先想到的就是递归,左子树递归,右子树递归等操作。
要求O(1)时间复杂度想到的就是Hash表,要求无额外空间使用,那就是原地算法。
字符串顺序颠倒,反转,想到手摇算法等等。
附一张LeetCode刷题情况(哈哈哈,很多都是补卡的)。

反正刷算法,最重要的应该就是perseverance。
数组
多维数组的原理、作用
多维数组的原理与作用
稀疏数组
稀疏数组
链表
单向链表的增删改查的具体实现思路
详解单链表的增删改查的实现
单向链表的CRUD
约瑟夫环问题(可不学)
约瑟夫环问题
双向链表
双向链表的CRUD
树
二叉搜索树
顺序与链式存储结构,前中后序以及层序遍历
中序线索二叉树
中序线索二叉树的实现
哈夫曼树的编码与译码
哈夫曼树的编码实现
哈夫曼树的译码实现
红黑树
B树
B+树
堆
顺序与链式结构队列实现
顺序与链式存储结构队列实现
优先队列排序算法(重点)
优先队列排序算法我第一次见到是再MySQL中。
对于MySQL5.6之后,会有一个算法叫做优先队列排序算法,大概方式就是维护一个大小为limit X中X数量的大顶堆,然后遍历所有数据并替换大顶堆的值,这样子就不需要对无用的数据进行排序了。并且我也在2023的考研题目中一眼就看到了基于优先队列排序算法的题目,所以我感觉这个算法思路还是很妙的。
栈
顺序存储结构与链式存储结构栈
顺序栈和链栈详解
代码实现与讲解
单调栈算法(可不学)
图
邻接矩阵与邻接表的深度优先遍历
图操作之邻接矩阵与邻接表的深度优先遍历
相关文章:

【考研408常用数据结构】C/C++实现代码汇总
文章目录 前言数组多维数组的原理、作用稀疏数组 链表单向链表的增删改查的具体实现思路约瑟夫环问题(可不学)双向链表 树二叉搜索树中序线索二叉树哈夫曼树的编码与译码红黑树B树B树 堆顺序与链式结构队列实现优先队列排序算法(重点…...

Flink学习笔记(二):Flink内存模型
文章目录 1、配置总内存2、JobManager 内存模型3、TaskManager 内存模型4、WebUI 展示内存5、Flink On YARN 模式下内存分配6、Flink On Yarn 集群消耗资源估算6.1、资源分配6.2、Flink 提交 Yarn 集群的相关命令6.3、Flink On Yarn 集群的资源计算公式 1、配置总内存 Flink J…...
信息系统项目管理师第四版学习笔记——项目绩效域
干系人绩效域 干系人绩效域涉及与干系人相关的活动和职能。在项目整个生命周期过程中,有效执行本绩效域可以实现的预期目标主要包含:①与干系人建立高效的工作关系;②干系人认同项目目标;③支持项目的干系人提高了满意度…...

PyTorch 深度学习之加载数据集Dataset and DataLoader(七)
1. Revision: Manual data feed 全部Batch:计算速度,性能有问题 1 个 :跨越鞍点 mini-Batch:均衡速度与性能 2. Terminology: Epoch, Batch-Size, Iteration DataLoader: batch_size2, sheffleTrue 3. How to define your Dataset 两种处…...

小谈设计模式(26)—中介者模式
小谈设计模式(26)—中介者模式 专栏介绍专栏地址专栏介绍 中介者模式分析角色分析抽象中介者(Mediator)具体中介者(ConcreteMediator)抽象同事类(Colleague)具体同事类(C…...

7种设计模式
1. 工厂模式 优点:封装了对象的创建过程,降低了耦合性,提供了灵活性和可扩展性。 缺点:增加了代码的复杂性,需要创建工厂类。 适用场景:当需要根据不同条件创建不同对象时,或者需要隐藏对象创建…...
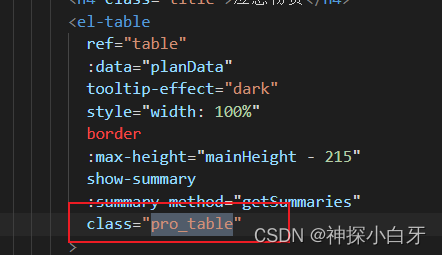
el-table合计行合并
效果如下 因为合计el-table的合并方法是不生效的,所以需要修改css下手 watch: {// 应急物资的合计合并planData: {immediate: true,handler() {setTimeout(() > {const tds document.querySelectorAll(".pro_table .el-table__footer-wrapper tr>td");tds[0]…...

新手如何快速上手HTTP爬虫IP?
对于刚接触HTTP爬虫IP的新手来说,可能会感到有些困惑。但是,实际上HTTP爬虫IP并不复杂,只要掌握了基本的操作步骤,就可以轻松使用。本文将为新手们提供一个快速上手HTTP爬虫IP的入门指南,帮助您迅速了解HTTP爬虫IP的基…...
(十五)VBA常用基础知识:正则表达式的使用
vba正则表达式的说明 项目说明Pattern在这里写正则表达式,例:[\d]{2,4}IgnoreCase大小写区分,默认false:区分;true:不区分Globaltrue:全体检索;false:最小匹配Test类似p…...

vue配置@路径
第一步:安装path,如果node_module文件夹中有path就不用安装了 安装命令:npm install path --save 第二步:在vue.config.js文件(如果没有就新建)中配置 const path require("path"); function …...
Ubuntu 18.04 OpenCV3.4.5 + OpenCV3.4.5 Contrib 编译
目录 1 依赖安装 2 下载opencv3.4.5及opencv3.4.5 contrib版本 3 编译opencv3.4.5 opencv3.4.5_contrib及遇到的问题 1 依赖安装 首先安装编译工具CMake,命令安装即可: sudo apt install cmake 安装Eigen: sudo apt-get install libeigen3-…...

【网络基础】IP 子网划分(VLSM)
目录 一、 为什么要划分子网 二、如何划分子网 1、划分两个子网 2、划分多个子网 一、 为什么要划分子网 假设有一个B类IP地址172.16.0.0,B类IP的默认子网掩码是 255.255.0.0,那么该网段内IP的变化范围为 172.16.0.0 ~ 172.16.255.255,即…...

【OCR】合同上批量贴印章
一、需求 OCR算法在处理合同等文件时,会由于印章等遮挡导致文本误识别。因此在OCR预处理时,有一个很重要的步骤是“去除印章”。其中本文主要聚焦在“去除印章”任务中的数据构建步骤:“合同伪印章”的数据构建。下面直接放几张批量合成后效果…...

Stable diffusion 用DeOldify给黑白照片、视频上色
老照片常常因为当时的技术限制而只有黑白版本。然而现代的 AI 技术,如 DeOldify,可以让这些照片重现色彩。 本教程将详细介绍如何使用 DeOldify 来给老照片上色。. 之前介绍过基于虚拟环境的 基于DeOldify的给黑白照片、视频上色,本次介绍对于新手比较友好的在Stable diff…...

在服务器上解压.7z文件
1. 更新apt sudo apt-get update2. 安装p7zip sudo apt-get install p7zip-full3. 解压.7z文件 7za x WN18RR.7z...

【opencv】windows10下opencv4.8.0-cuda C++版本源码编译教程
【opencv】windows10下opencv4.8.0-cuda C版本源码编译教程 提示:博主取舍了很多大佬的博文并亲测有效,分享笔记邀大家共同学习讨论 文章目录 【opencv】windows10下opencv4.8.0-cuda C版本源码编译教程前言准备工具cuda/cudnncmakeopencv4.8.0opencv_contrib CMake编译VS2019编…...
软碟通制作启动盘
一、下载并安装软碟通 二、插入U盘,打开软碟通; 三、在软碟通中选择“文件”-“打开镜像文件”,选择要制作成启动盘的ISO镜像文件; 1.打开要制作的iso文件 选择对应的iso文件 四、在软碟通中选择“启动”-“写入硬盘”ÿ…...
Tomcat和HPPT协议
1.介绍 1.Java EE 规范 JavaEE(java Enterprise Edition):java企业版 JavaEE 规范是很多的java开发技术的总称。这些技术规范都是沿用自J2EE的。一共包括了13个技术规范 2.WEB概述 WEB在计算机领域中代表的是网络 像我们之前所用的WWW&…...
)
Acwing.4736步行者(模拟)
题目 约翰参加了一场步行比赛。 比赛为期 N 天,参赛者共 M 人(包括约翰)。 参赛者编号为 1∼M,其中约翰的编号为 P。 每个参赛者的每日步数都将被赛事方记录并公布。 每日步数最多的参赛者是当日的日冠军(可以有并…...
前端预览、下载二进制文件流(png、pdf)
前端请求设置 responseType: “blob” 后台接口返回的文件流如下: 拿到后端返回的文件流后: 预览 <iframe :src"previewUrl" frameborder"0" style"width: 500px; height: 500px;"></iframe>1、预览 v…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
