零基础学python之元组
文章目录
- 元组
- 1、元组的应用场景
- 2、定义元组
- 3、元组的常见操作
- 4、总结
元组
- 目标
- 元组的应用场景
- 定义元组
- 元组常见操作
1、元组的应用场景
思考:如果想要存储多个数据,但是这些数据是不能修改的数据,怎么做?
答:列表?列表可以一次性存储多个数据,但是列表中的数据允许更改。
num_list = [10, 20, 30]
num_list[0] = 100
一个元组可以存储多个数据,元组内的数据是不能修改的
2、定义元组
元组特点:定义元组使用小括号,且逗号隔开各个数据,数据可以是不同的数据类型。
# 多个数据元组
t1 = (10, 20, 30)# 单个数据元组
t2 = (10,)
注意:如果定义的元组只有一个数据,那么这个数据后面也好添加逗号,否则数据类型为唯一的这个数据的数据类型
t2 = (10,)
print(type(t2)) # tuplet3 = (20)
print(type(t3)) # intt4 = ('hello')
print(type(t4)) # str
3、元组的常见操作
元组数据不支持修改,只支持查找,具体如下:
- 按下标查找数据
tuple1 = ('aa', 'bb', 'cc', 'bb')
print(tuple1[0]) # aa
- index():查找某个数据,如果数据存在返回对应的下标,否则报错,语法和列表、字符串的index方法相同。
tuple1 = ('aa', 'bb', 'cc', 'bb')
print(tuple1.index('aa')) # 0
- count():统计某个数据在当前元组出现的次数。
tuple1 = ('aa', 'bb', 'cc', 'bb')
print(tuple1.count('bb')) # 2
- len():统计元组中数据的个数。
tuple1 = ('aa', 'bb', 'cc', 'bb')
print(len(tuple1)) # 4
注意:元组内的直接数据如果修改则立即报错
tuple1 = ('aa', 'bb', 'cc', 'bb')
tuple1[0] = 'aaa'
但是如果元组里面有列表,修改列表里面的数据则是支持的
tuple2 = (10, 20, ['aa', 'bb', 'cc'], 50, 30)
print(tuple2[2]) # 访问到列表# 结果:(10, 20, ['aaaaa', 'bb', 'cc'], 50, 30)
tuple2[2][0] = 'aaaaa'
print(tuple2)# 结果: (10, 20, ['aaaaa', 'bb', 'cc'], 50, 30)
4、总结
- 定义元组
t1 = (10, 20, 30)
t2 = (10,) # 定义只有一个数据的元组
- 常用操作方法
- index()
- len()
相关文章:

零基础学python之元组
文章目录 元组1、元组的应用场景2、定义元组3、元组的常见操作4、总结 元组 目标 元组的应用场景定义元组元组常见操作 1、元组的应用场景 思考:如果想要存储多个数据,但是这些数据是不能修改的数据,怎么做? 答:列…...

11. SpringBoot项目中参数获取与响应
SpringBoot项目中参数获取与响应 1. 程序结构&通信方式 程序结构: C/S : 客户端/服务器端 -Main方法。 -效果炫目、数据相对安全。 -公司成本高,因为要分别开发客户端和服务器端。 B/S: 浏览器端/服务器端 -效果依赖于浏览…...
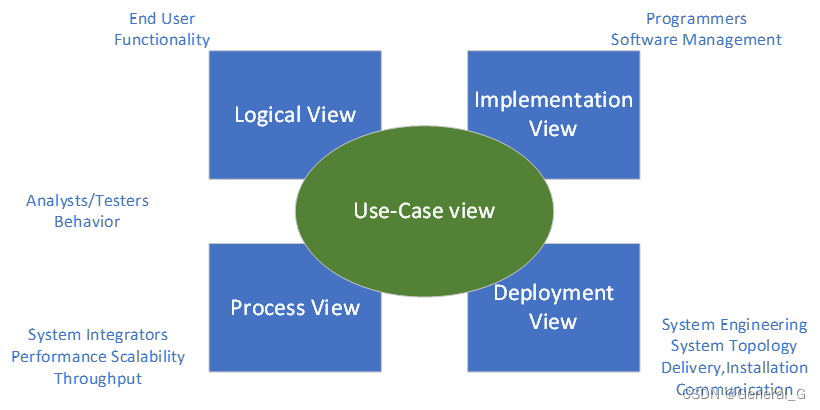
4+1视图与UML
目录 逻辑视图过程视图开发视图物理视图(部署视图)用例视图 41视图,即逻辑视图,过程视图,实现视图,部署视图,用例视图。 为什么不用一个视图? 针对多个用户,即终端用户&a…...

没用的知识增加了,尝试用文心实现褒义词贬义词快速分类
尝试用文心实现褒义词贬义词快速分类 一、我的需求二、项目环境搭建千帆SDK安装及使用流程 三、项目实现过程创建应用获取签名调用接口计算向量积总结 百度世界大会将于10月17日在北京首钢园举办,今天进入倒计时五天了。通过官方渠道的信息了解到,这次是…...
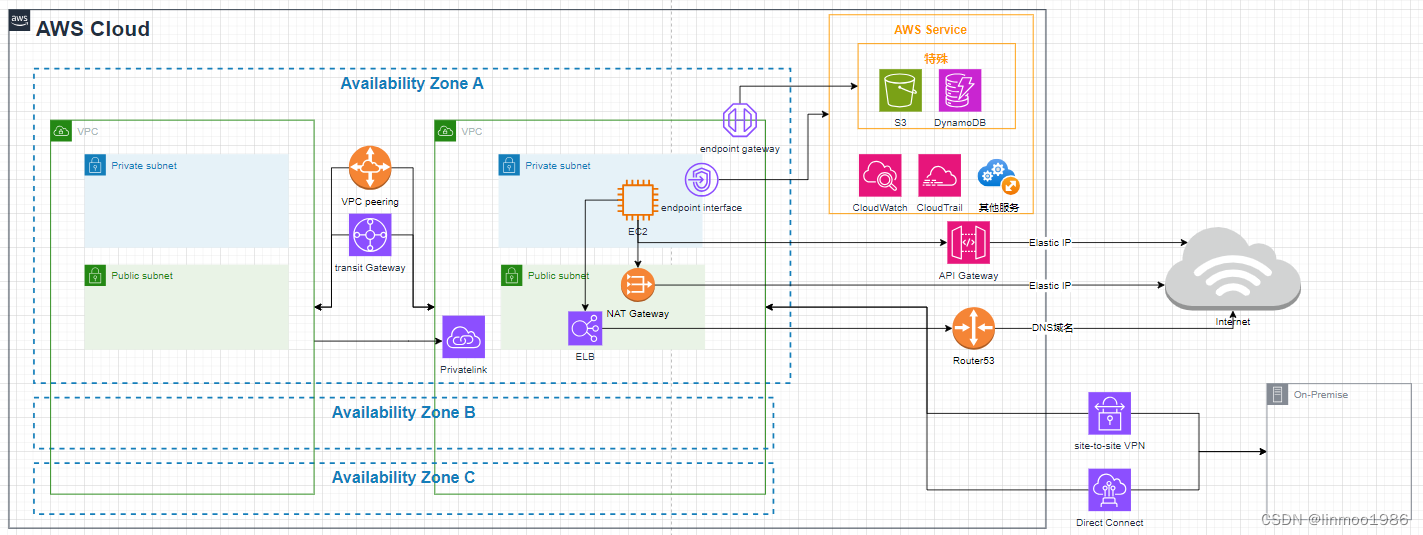
AWS SAP-C02教程3--网络资源
架构设计中网络也是少不了的一个环节,而AWS有自身的网络结构和网络产品。本章中将带你看看AWS中不同网络产品,以及计算资源、存储资源等产品在网络架构中处于哪个位置,如何才能让它们与互联网互通、与其它产品互通。下图视图将SAP涉及到网络相关组件在一张图表示出来,图中可…...

【TensorFlow2 之012】TF2.0 中的 TF 迁移学习
#012 TensorFlow 2.0 中的 TF 迁移学习 一、说明 在这篇文章中,我们将展示如何在不从头开始构建计算机视觉模型的情况下构建它。迁移学习背后的想法是,在大型数据集上训练的神经网络可以将其知识应用于以前从未见过的数据集。也就是说,为什么…...

mysql面试题46:MySQL中datetime和timestamp的区别
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:MySQL中DATETIME和TIMESTAMP的区别 在MySQL中,DATETIME和TIMESTAMP是两种用于存储日期和时间的数据类型。虽然它们都可以用于存储日期和时间信息…...

【Spring Boot】RabbitMQ消息队列 — RabbitMQ入门
💠一名热衷于分享知识的程序员 💠乐于在CSDN上与广大开发者交流学习。 💠希望通过每一次学习,让更多读者了解我 💠也希望能结识更多志同道合的朋友。 💠将继续努力,不断提升自己的专业技能,创造更多价值。🌿欢迎来到@"衍生星球"的CSDN博文🌿 🍁本…...
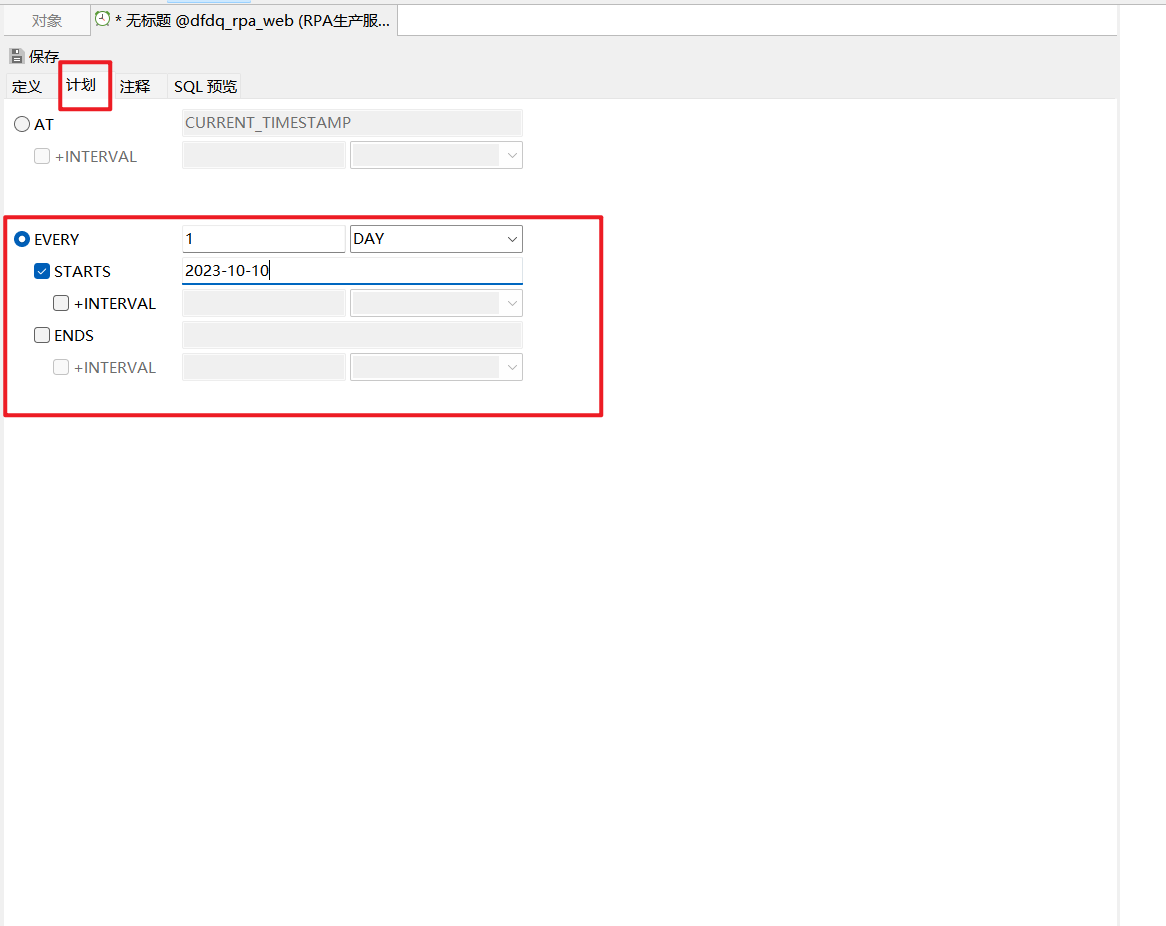
Navicat定时任务
Navicat定时任务 1、启动Navicat for MySQL工具,连接数据库。 2、查询定时任务选项是否开启 查询命令:SHOW VARIABLES LIKE ‘%event_scheduler%’; ON表示打开,OFF表示关闭。 打开定时任务命令 SET GLOBAL event_scheduler 0; 或者 SET G…...
小白必备:简单几步, 使用Cpolar+Emlog在Ubuntu上搭建个人博客网站
文章目录 前言1. 网站搭建1.1 Emolog网页下载和安装1.2 网页测试1.3 cpolar的安装和注册 2. 本地网页发布2.1 Cpolar临时数据隧道2.2.Cpolar稳定隧道(云端设置)2.3.Cpolar稳定隧道(本地设置) 3. 公网访问测试总结 前言 博客作为使…...

封装 Token
什么是token? 作为计算机术语,是“令牌”的意思 。 Token 是服务端生成的一串字符串,以作客户端进行请求的一个令牌,当第一次登录后,服务器生成一个Token便将此Token返回给客户端,以后客户端只需带上这个Token前来请…...
——点云添加均匀分布的随机噪声)
CloudCompare 二次开发(17)——点云添加均匀分布的随机噪声
目录 一、概述二、代码集成三、结果展示一、概述 不依赖任何第三方点云相关库,使用CloudCompare编程实现点云添加随机噪声。添加随机噪声的算法原理见:PCL 点云添加均匀分布的随机噪声。 二、代码集成 1、mainwindow.h文件public中添加: void doActionAddRandomNoise(); …...

研发必会-异步编程利器之CompletableFuture(含源码 中)
近期热推文章: 1、springBoot对接kafka,批量、并发、异步获取消息,并动态、批量插入库表; 2、SpringBoot用线程池ThreadPoolTaskExecutor异步处理百万级数据; 3、基于Redis的Geo实现附近商铺搜索(含源码) 4、基于Redis实现关注、取关、共同关注及消息推送(含源码) 5…...
上海亚商投顾:沪指高开高走 锂电等新能源赛道大反攻
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 沪指昨日高开后强势震荡,创业板指盘中一度翻绿,随后探底回升再度走高。碳酸锂期货合约…...
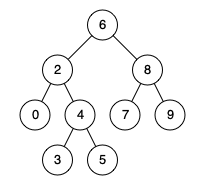
力扣第235题 二又搜索树的最近公共祖先 c++
题目 235. 二叉搜索树的最近公共祖先 中等 (简单) 相关标签 树 深度优先搜索 二叉搜索树 二叉树 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q&…...

时代风口中的Web3.0基建平台,重新定义Web3.0!
近年来,Web3.0概念的广泛兴起,给加密行业带来了崭新的叙事方式,同时也为加密行业提供了更加具有想象力的应用场景与商业空间,并让越来越多的行业从业者们意识到只有更大众化的市场共性需求才能推动加密市场的持续繁荣。当前围绕这…...
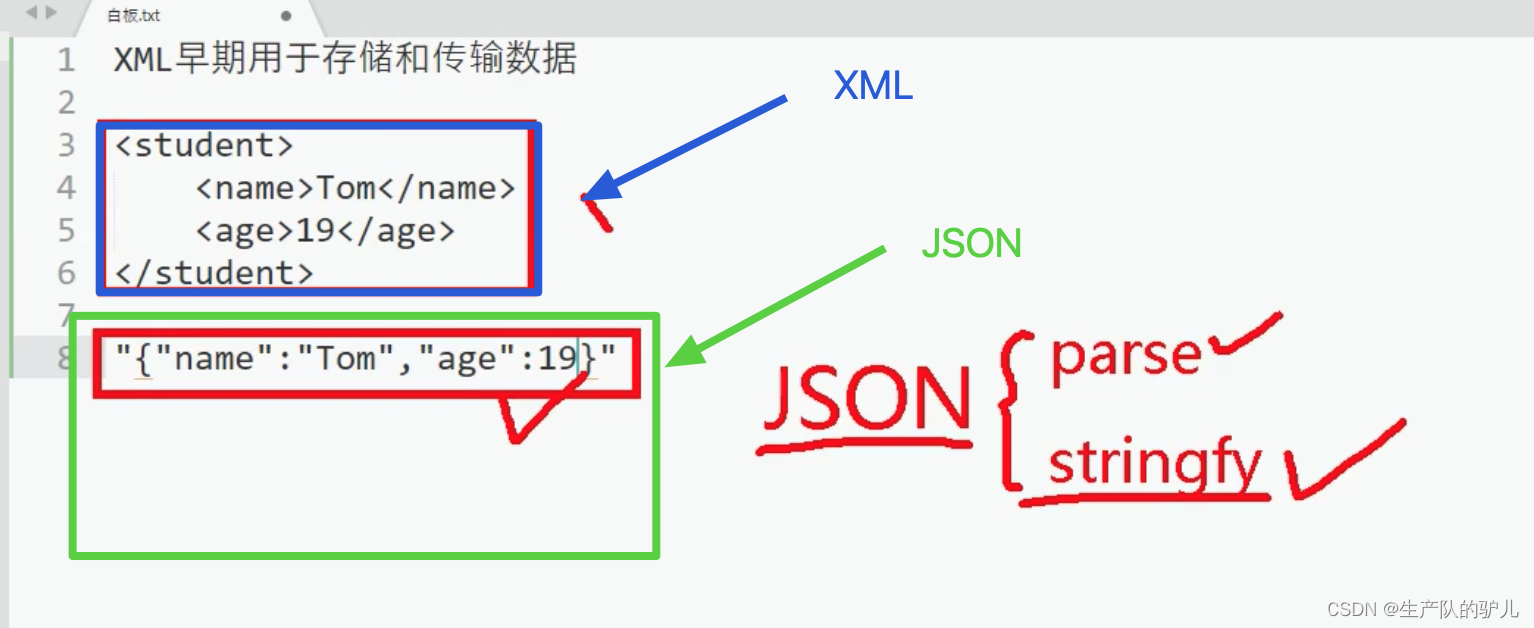
React学习笔记 001
什么是React 1.发送请求获取数据 处理数据(过滤、整理格式等) 3.操作DOM呈现页面 react 主要是负责第三部 操作dom 处理页面 数据渲染为HTML视图的开源js库。 好处 避免dom繁琐 组件化 提升复用率 特点 声明式编程: 简单 组件化编程…...
2023 | github无法访问或速度慢的问题解决方案
github无法访问或速度慢的问题解决方案 前言: 最近经常遇到github无法访问, 或者访问特别慢的问题, 在搜索了一圈解决方案后, 有些不再有效了, 但是其中有几个还特别好用, 总结一下. 首选方案 直接在github.com的域名上加一个fast > githubfast.com, 访问的是与github完全相…...
unity各种插件集合(自用)
2D Animation——2D序列帧/骨骼动画相关 2D PSD Importer——psb骨骼动画(unity官方建议使用psb而非psd) (Advanced —show preview package 勾选)出现 2D IK——反向动力学IK Universal RP——升级项目到Urp(通用渲…...
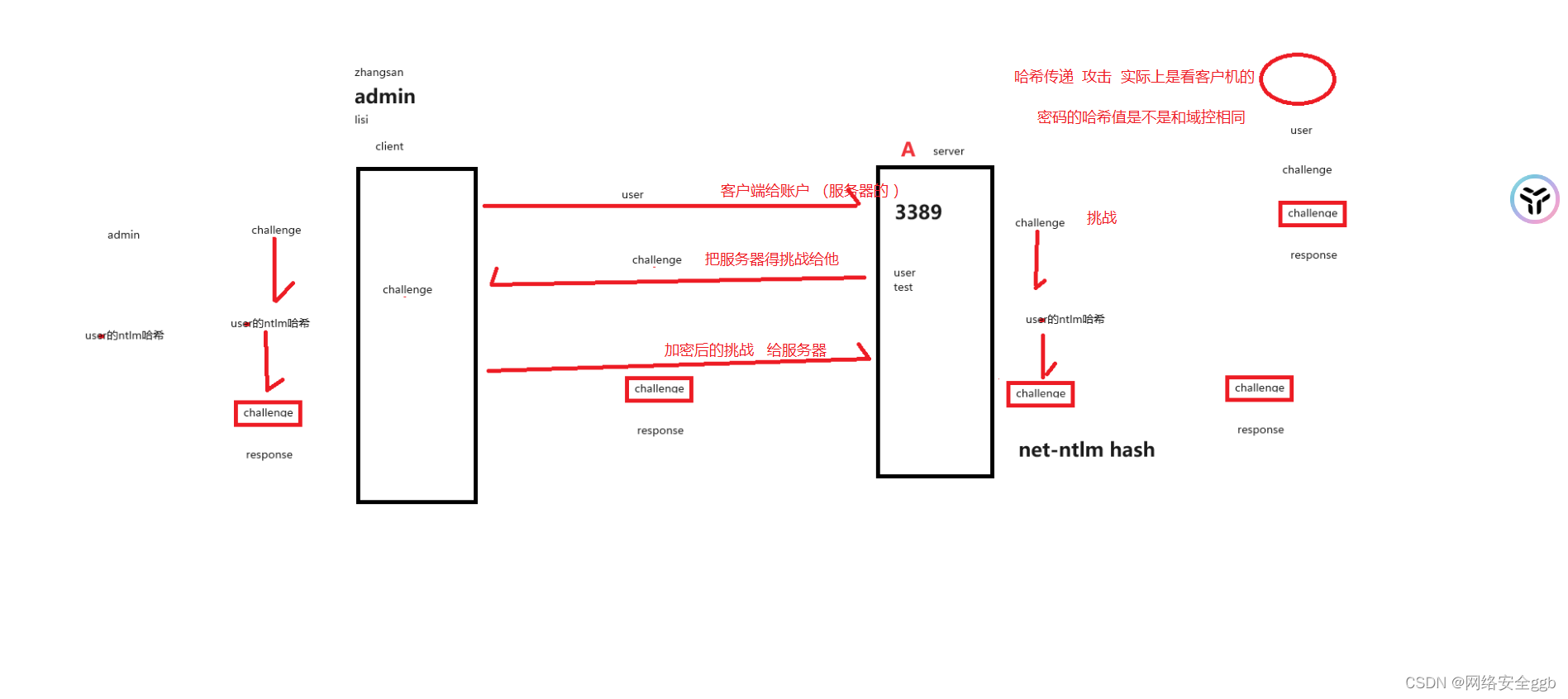
内网收集哈希传递
1.内网收集的前提 获得一个主机权限 补丁提权 可以使用 systeminfo 然后使用python脚本找到缺少的补丁 下载下来 让后使用exp提权 收集信息 路由信息 补丁接口 dns域看一看是不是域控 扫描别的端口 看看有没有内在的web网站 哈希传递 哈希是啥 哈希…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
