数据结构和算法——查找算法
目录
线性查找法
二分查找法
插值查找法
斐波那契查找法
线性查找法
可以是有序的,也可以是无序的。
public class SeqSearch {public static void main(String[] args) {int[] arr = new int[]{1, 9, 11, -1, 34, 89};int res = seqSearch(arr, 34);}public static int seqSearch(int[] arr, int n) {for (int i = 0; i < arr.length; i++) {if (arr[i] == n) {return i;}}return -1;}
}
二分查找法
也叫折半查找,数组必须有序。
public class BinarySearch {public static void main(String[] args) {int[] arr = new int[]{2, 2, 4, 4, 5};
// int res = binarySearch(arr, 6);List list = binarySearchPlus(arr, 6);}public static int binarySearch(int[] arr, int n) {int l = 0;int r = arr.length - 1;while (l <= r) {int m = (l + r) / 2;if (n < arr[m]) {r = m - 1;} else if (n > arr[m]) {l = m + 1;} else if (n == arr[m]) {return m;} else {return -1;}}return -1;}public static ArrayList binarySearchPlus(int[] arr, int n) {int l = 0;int r = arr.length - 1;while (l <= r) {int m = (l + r) / 2;if (n < arr[m]) {r = m - 1;} else if (n > arr[m]) {l = m + 1;} else if (n == arr[m]) {ArrayList<Integer> list = new ArrayList<>();list.add(m);for (int i = m - 1; i >= 0 && n == arr[i]; i++) {list.add(i);}for (int i = m + 1; i < arr.length && n == arr[i]; i++) {list.add(i);}Collections.sort(list);return list;} else {return null;}}return null;}
}
插值查找法
斐波那契查找法
相关文章:

数据结构和算法——查找算法
目录 线性查找法 二分查找法 插值查找法 斐波那契查找法 线性查找法 可以是有序的,也可以是无序的。 public class SeqSearch {public static void main(String[] args) {int[] arr new int[]{1, 9, 11, -1, 34, 89};int res seqSearch(arr, 34);}public st…...

Blender:对模型着色
Blender:使用立方体制作动漫头像-CSDN博客 上一步已经做了一个头像模型,我做的太丑了,就以这个外星人头像为例 首先切换到着色器编辑器 依次搜索:纹理坐标、映射、分离xyz和颜色渐变 这里的功能也是非常丰富和强大,…...

加密市场波动:地缘政治与美股走弱引发不确定性!
伴随着国庆假期的结束,多日波动率维持低位的加密市场也似乎开始苏醒。近期多次突破28000美元未果的比特币,于9日15:00开始从27800美元附近下跌,最低跌至27260美元,同期以太坊也至1550美元左右,创近半个月来新低。 Coin…...
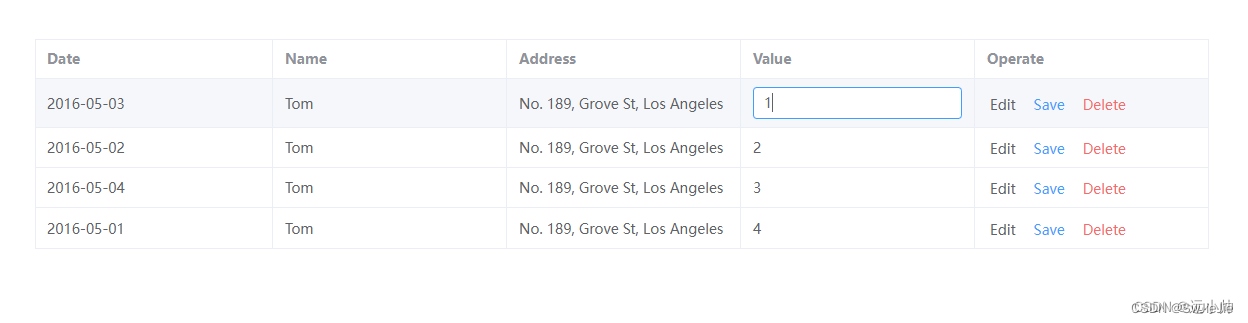
ElementUI编辑表格单元格与查看模式切换的应用
需求:有时候在填写表单的时候,想要在输入的时候是input输入框的状态,但是当鼠标移出输入框失去焦点时,希望是查看的状态,这种场景可以通过 v-if实现 vue2ElementUi里面使用如下: 1.el-table标签注册 cell-…...

spring-创建Webservice服务
Web service是一个平台独立的,松耦合的,自包含的、基于可编程的web的应用程序,可使用开放的XML标准来描述、发布、发现、协调和配置这些应用程序,用于开发分布式的互操作的应用程序。webservice用的是soap协议。 客户通过发送请求…...
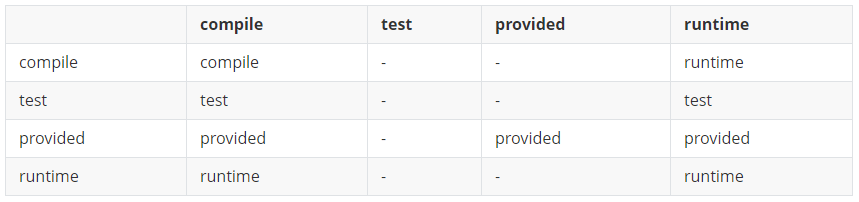
Maven系列第3篇:详解maven解决依赖问题
maven系列目标:从入门开始开始掌握一个高级开发所需要的maven技能。 这是maven系列第3篇。 我们先来回顾一下什么是maven? maven是apache软件基金会组织维护的一款自动化构件工具,专注服务于java平台的项目构件和依赖管理。 本文主要内容…...

读书笔记:多Transformer的双向编码器表示法(Bert)-4
多Transformer的双向编码器表示法 Bidirectional Encoder Representations from Transformers,即Bert; 第二部分 探索BERT变体 从本章开始的诸多内容,以理解为目标,着重关注对音频相关的支持(如果有的话)…...

Stable Diffusion XL搭建
本文参考:Stable Diffusion XL1.0正式发布了,赶紧来尝鲜吧-云海天教程 Stable Diffision最新模型SDXL 1.0使用全教程 - 知乎 1、SDXL与SD的区别 (1)分辨率得到了提升 原先使用SD生成图片,一般都是生成512*512&…...
:性能优化之PureComponent和memo)
面试题-React(十一):性能优化之PureComponent和memo
一、React性能优化的重要性 随着应用的复杂性增加,React组件的渲染可能成为性能瓶颈。频繁的渲染可能导致不必要的性能开销和卡顿。为了确保应用的高性能和流畅用户体验,我们需要采取一些措施来优化组件的渲染。 二、PureComponent-自动浅比较 PureCo…...
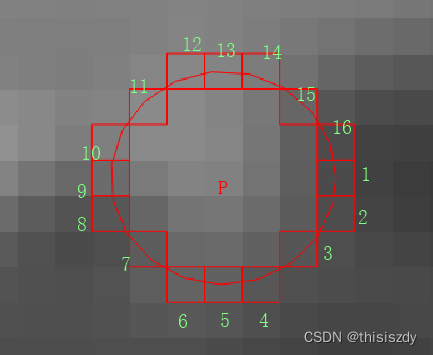
<图像处理> Fast角点检测
Fast角点检测 基本原理是使用圆周长为N个像素的圆来判定其圆心像素P是否为角点,如下图所示为圆周长为16个像素的圆(半径为3);OpenCV还提供圆周长为12和8个像素的圆来检测角点。 相对中心像素的位置信息 //圆周长为16 static c…...

基于centos、alpine制作Java JDK基础镜像
文章目录 前言一、 简介二、制作JDK/Java基础镜像1.准备事项2.制作Dockerfile脚本2.1.基于centos作为基础镜像2.2.基于alpine作为基础镜像3.构建镜像4.测试验证前言 在日常开发中,但凡项目需要docker容器化部署,制作项目镜像前都需要在Dockerfile中配置Java基础镜像。为什么…...

【AI视野·今日Robot 机器人论文速览 第五十二期】Wed, 11 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Wed, 11 Oct 2023 Totally 31 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers RoboHive: A Unified Framework for Robot Learning Authors Vikash Kumar, Rutav Shah, Gaoyue Zhou, Vincent Moens, Vittor…...
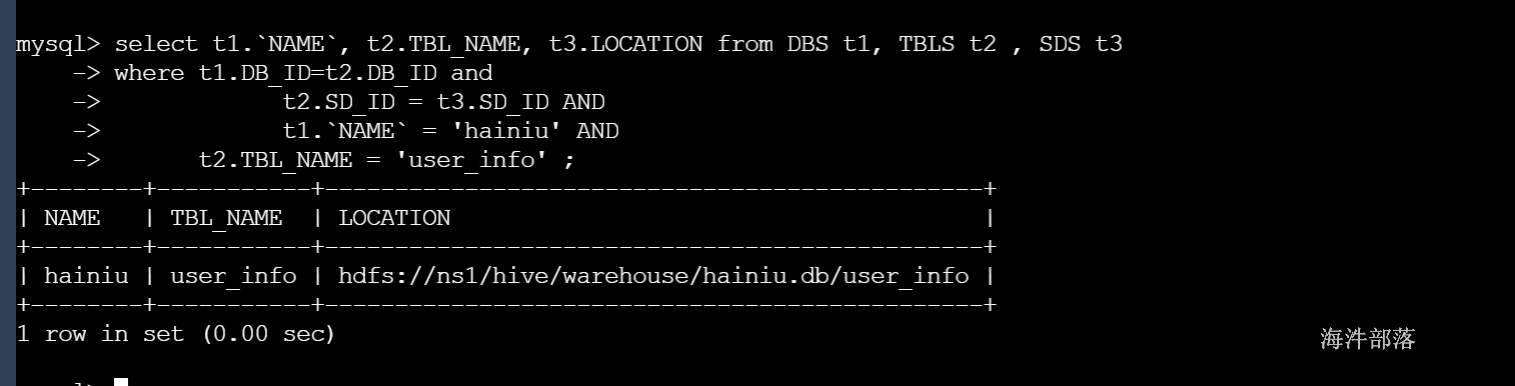
hive 知识总结
编辑 社区公告教程下载分享问答JD 登 录 注册 01 hive 介绍与安装 1 hive介绍与原理分析 Hive是一个基于Hadoop的开源数据仓库工具,用于存储和处理海量结构化数据。它是Facebook 2008年8月开源的一个数据仓库框架,提供了类似于SQL语法的HQL…...

golang/云原生/Docker/DevOps/K8S/持续 集成/分布式/etcd 教程
3-6个月帮助学员掌握golang后端开发岗位必备技术点 教程时长: 150小时 五大核心专栏,原理源码案例分析项目实战直击工作岗位 golang:解决go语言编程问题 工程组件:解决golang工程化问题 分布式中间件:解决技术栈单一及分布式开发问题 云原生…...
jeecg库login登录过程分析笔记
jeecg库(版本jeecg-boot-v3.5.1last)实现了用户登录功能,二开时为了借鉴jeecg用户登录的方法,跑了一遍登录方法: org.jeecg.modules.system.controller.LoginController#login 定义这个方法的类的路径是:…...
echarts仪表盘vue
<div class"ybptx" ref"btryzb"></div>mounted() {this.getBtData();},getBtData() {var chart this.$echarts.init(this.$refs.btryzb);var data_czzf 88;var option {series: [{name: 内层数据刻度,type: gauge,radius: 80%,min: 0,max: 1…...

管道和重定向分号-连接符
本文介绍shell脚本常用命令连接符:管道符( | )、重定向( < 、>、>>、2> 、&> )、分号( ; ) 本文内容同微信公众号【凡登】,关注不迷路,学习上高速,欢迎关注共同学习。 1、管道 进程的通信方式之一…...
)
WSL VScode连接文件后无法修改(修改报错)
权限问题 usrname:用户名 dirpath:要修改的文件夹路径 sudo chown -R usrname /dirpath...
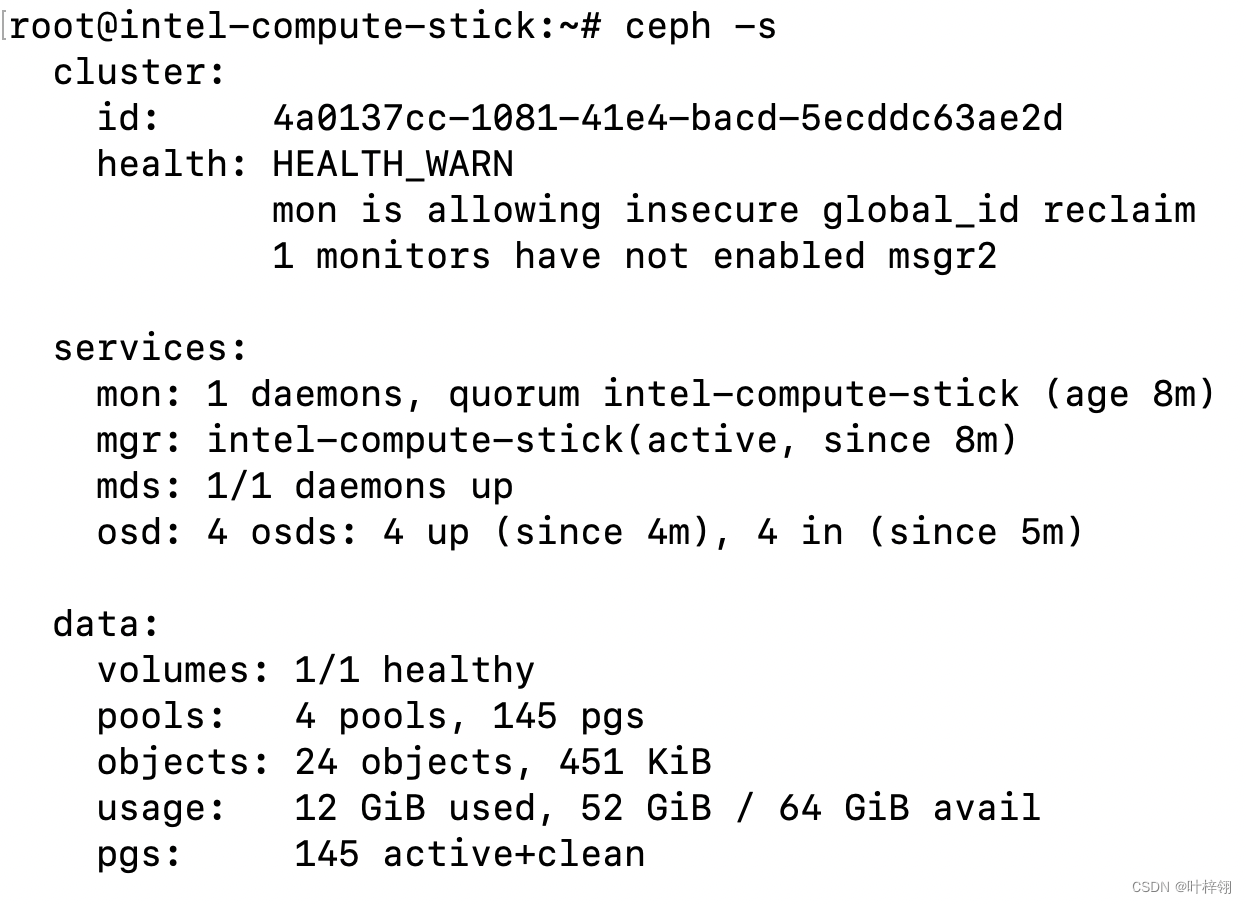
迷你Ceph集群搭建(超低配设备)
我的博客原文链接:https://blog.gcc.ac.cn/post/2023/%E8%BF%B7%E4%BD%A0ceph%E9%9B%86%E7%BE%A4%E6%90%AD%E5%BB%BA/ 环境 机器列表: IP角色说明10.0.0.15osdARMv7,512M内存,32G存储,百兆网口10.0.0.16clientARM64…...

Python数据挖掘项目实战——自动售货机销售数据分析
摘要:本案例将主要结合自动售货机的实际情况,对销售的历史数据进行处理,利用pyecharts库、Matplotlib库进行可视化分析,并对未来4周商品的销售额进行预测,从而为企业制定相应的自动售货机市场需求分析及销售建议提供参…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
