优化|优化处理可再生希尔伯特核空间的非参数回归中的协变量偏移

原文:Optimally tackling covariate shift in RKHS-based nonparametric regression. The Annals of Statistics, 51(2), pp.738-761, 2023.
原文作者:Cong Ma, Reese Pathak, Martin J. Wainwright
论文解读者:赵进
编者按:
在再生核希尔伯特空间(RKHS)框架下,本文深入研究了非参数回归的协变量转移问题。特别地,其集中讨论了两类主要的协变量转移问题,它们均由源与目标分布间的似然比所定义。当这些似然比受到均匀上界约束时,文章证明,对于一个具有规范化核特征值的广泛RKHS类,精确调整的正则化参数下的核岭回归(KRR)估计函数是极小极大最优的(仅有对数因子的差异)。值得注意的是,除其上确界外,KRR并不依赖于似然比的完整信息。接下来,针对似然比无上界限制但其第二矩有限的更复杂情况,文章提出了一种基于似然比率的有限截断策略的加权KRR估计方法。并且进一步证实,此估计方法在最小最大意义上达到了最优性,仅存在对数级的差异。
1. 问题背景
1.1 协变量转移下的非参数回归
非参数回归的主旨在于依赖于协变量向量 X ∈ X X\in\mathcal{X} X∈X来预测实数值反应 Y Y Y. 对于每一特定的 x x x, 均方误差最优的估计器由回归函数 f ∗ ( x ) : = E [ Y ∣ X = x ] f^{*}(x):=\mathbb{E}[Y | X = x] f∗(x):=E[Y∣X=x]所描述. 在常规的研究背景中, 我们假设能观察到 n n n个独立同分布的样本对 { ( x i , y i ) } i = 1 n \{(x_{i}, y_{i})\}_{i=1}^{n} {(xi,yi)}i=1n, 其中每个 x i x_{i} xi是按照分布 P P P在 X \mathcal{X} X上抽样得到的,随后 y i y_i yi 是根据条件概率 ( Y ∣ X = x i ) (Y | X=x_i) (Y∣X=xi) 抽样得到的. 我们始终设定, 对于每一个 i i i, 其残差 ω i : = y i − f ∗ ( x i ) \omega_{i} := y_i - f^*(x_i) ωi:=yi−f∗(xi)是具有方差 σ 2 \sigma^2 σ2的次高斯型随机变量.
我们将协变量空间上的分布 P P P称为源分布. 在标准设定中, 估计函数 f ^ \hat{f} f^的性能是根据其 L 2 ( P ) L^2(P) L2(P)误差来衡量的:
∥ f ^ − f ⋆ ∥ P 2 : = E X ∼ P ( f ^ ( X ) − f ⋆ ( X ) ) 2 = ∫ X ( f ^ ( x ) − f ⋆ ( x ) ) 2 p ( x ) d x , \|\hat{f}-f^{\star}\|_P^2 := \mathbb{E}_{X \sim P}(\hat{f}(X)-f^{\star}(X))^2=\int_{\mathcal{X}}(\hat{f}(x)-f^{\star}(x))^2 p(x) d x, ∥f^−f⋆∥P2:=EX∼P(f^(X)−f⋆(X))2=∫X(f^(x)−f⋆(x))2p(x)dx,
其中 p p p是 P P P的密度函数, L 2 ( P ) L^2(P) L2(P)是以 P P P为概率测度的 L 2 L_{2} L2空间.
在协变量转移下, 我们希望构建一个估计函数 f ^ \hat{f} f^, 其 L 2 ( Q ) L^2(Q) L2(Q)误差很小. 在此, 目标分布 Q Q Q与源分布 P P P不同. 从分析角度来看, 设 q q q为 Q Q Q的密度, 我们的目标是找到估计函数 f ^ \hat{f} f^, 使
∥ f ^ − f ⋆ ∥ Q 2 : = E X ∼ Q ( f ^ ( X ) − f ⋆ ( X ) ) 2 = ∫ X ( f ^ ( x ) − f ⋆ ( x ) ) 2 q ( x ) d x \|\hat{f}-f^{\star}\|_Q^2 := \mathbb{E}_{X \sim Q}(\hat{f}(X) - f^{\star}(X))^2 = \int_{\mathcal{X}}(\hat{f}(x) - f^{\star}(x))^2 q(x) d x ∥f^−f⋆∥Q2:=EX∼Q(f^(X)−f⋆(X))2=∫X(f^(x)−f⋆(x))2q(x)dx
尽可能小. 显然,此问题的难度取决于源分布和目标分布之间的某种差异性.
1.2 源-目标似然比上的条件
我们通过似然比来衡量 L 2 ( P ) L^2(P) L2(P)和 L 2 ( Q ) L^2(Q) L2(Q)之间的差异:
ρ ( x ) : = q ( x ) p ( x ) , \rho(x):=\frac{q(x)}{p(x)}, ρ(x):=p(x)q(x),
我们假设对于任意 x ∈ X x\in\mathcal{X} x∈X, ρ ( x ) \rho(x) ρ(x)存在. 通过对似然比施加不同的条件, 我们可以定义不同的源-目标对 ( P , Q ) (P, Q) (P,Q), 我们主要关注两种类型:
均匀 B B B-有界 对于 B ≥ 1 B\geq1 B≥1, 我们称似然比是 B B B-有界的, 如果
sup x ∈ X ρ ( x ) ≤ B , \sup _{x \in \mathcal{X}} \rho(x) \leq B, x∈Xsupρ(x)≤B,
可以看到, B = 1 B=1 B=1表示没有协变量转移的情况, 即 P = Q P=Q P=Q.
χ 2 \chi^2 χ2-有界 实际中, 均匀有界条件往往过于严格, 我们有必要考虑更宽松的条件. 一个放宽的方法是在二阶矩上进行限制. 我们称似然比是 V 2 V^2 V2-时刻有界的, 如果
E X ∼ P [ ρ 2 ( X ) ] ≤ V 2 . \mathbb{E}_{X \sim P}\left[\rho^2(X)\right] \leq V^2 . EX∼P[ρ2(X)]≤V2.
1.3 无权估计与似然加权估计的对比
本文关注基于在再生核定义的希尔伯特空间 H \mathcal{H} H上优化的非参数回归方法。希尔伯特范数 ∥ f ∥ H \|f\|_{\mathcal{H}} ∥f∥H被用作对解决方案施加“平滑性”的手段,无论是通过向目标函数增加一个惩罚项还是通过明确的约束.
在似然比未知的情况下, 一个直接的方法是简单地计算无权的正则化估计值
f ^ λ : = arg min f ∈ H { 1 n ∑ i = 1 n ( f ( x i ) − y i ) 2 + λ ∥ f ∥ H 2 } , \widehat{f}_\lambda := \arg \min _{f \in \mathcal{H}}\left\{\frac{1}{n} \sum_{i=1}^n\left(f\left(x_i\right)-y_i\right)^2+\lambda\|f\|_{\mathcal{H}}^2\right\}, f λ:=argf∈Hmin{n1i=1∑n(f(xi)−yi)2+λ∥f∥H2},
其中, λ > 0 \lambda>0 λ>0是用户定义的正则化参数。当 H \mathcal{H} H是一个再生核希尔伯特空间(RKHS)时,此估计被称为核岭回归(KRR)估计. 这是经验风险最小化的一种形式, 但在协变量转移存在的情境下, 目标涉及对 E P [ ( Y − f ( X ) ) 2 ] \mathbb{E}_{P}[(Y - f(X))^2] EP[(Y−f(X))2] 的经验近似, 而不是 E Q [ ( Y − f ( X ) ) 2 ] \mathbb{E}_{Q}[(Y - f(X))^2] EQ[(Y−f(X))2].
假如似然比已知,那么一个自然的建议是计算似然比加权的正则化估计,
f ~ λ r w : = arg min f ∈ H { 1 n ∑ i = 1 n ρ ( x i ) ( f ( x i ) − y i ) 2 + λ ∥ f ∥ H 2 } . \tilde{f}_\lambda^{\mathrm{rw}}:=\arg \min _{f \in \mathcal{H}}\left\{\frac{1}{n} \sum_{i=1}^n \rho\left(x_i\right)\left(f\left(x_i\right)-y_i\right)^2+\lambda\|f\|_{\mathcal{H}}^2\right\}. f~λrw:=argf∈Hmin{n1i=1∑nρ(xi)(f(xi)−yi)2+λ∥f∥H2}.
引入似然比确保了目标现在提供了对期望值 E Q [ ( Y − f ( X ) ) 2 ] \mathbb{E}_Q\left[(Y-f(X))^2\right] EQ[(Y−f(X))2]的无偏估计. 然而, 通过似然比进行重新加权也增加了方差,尤其是在似然比无界的情况下.
1.4 核函数及其特征值
任何RKHS都与一个半正定核函数 K : X × X → R \mathscr{K}: \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R} K:X×X→R 相关. Mercer定理保证该核函数具有以下形式的特征展开
K ( x , x ′ ) = ∑ j = 1 ∞ μ j ϕ j ( x ) ϕ j ( x ′ ) . \mathscr{K}\left(x, x^{\prime}\right) = \sum_{j=1}^{\infty} \mu_j \phi_j(x) \phi_j\left(x^{\prime}\right). K(x,x′)=j=1∑∞μjϕj(x)ϕj(x′).
其中, { μ j } j ≥ 1 \left\{\mu_j\right\}_{j \geq 1} {μj}j≥1为非负特征值序列, 而 { ϕ j } j ≥ 1 \left\{\phi_j\right\}_{j \geq 1} {ϕj}j≥1是在 L 2 ( Q ) L^2(Q) L2(Q)中正交的特征函数.
基于Mercer定理, RKHS范数的平方可以表示为:
∥ f ∥ H 2 = ∑ j = 1 ∞ θ j 2 μ j , θ j = ∫ X f ( x ) ϕ j ( x ) q ( x ) d x . \|f\|_{\mathcal{H}}^2=\sum_{j=1}^{\infty} \frac{\theta_j^2}{\mu_j}, \quad \theta_j=\int_{\mathcal{X}} f(x) \phi_j(x) q(x) d x. ∥f∥H2=j=1∑∞μjθj2,θj=∫Xf(x)ϕj(x)q(x)dx.
因此, 该希尔伯特空间 H \mathcal{H} H可以表示为
H : = { f = ∑ j = 1 ∞ θ j ϕ j ∣ ∑ j = 1 ∞ θ j 2 μ j < ∞ } . \mathcal{H}:=\left\{f=\sum_{j=1}^{\infty} \theta_j \phi_j \mid \sum_{j=1}^{\infty} \frac{\theta_j^2}{\mu_j}<\infty\right\}. H:={f=j=1∑∞θjϕj∣j=1∑∞μjθj2<∞}.
这篇论文的结果要求核函数 κ \kappa κ-均匀有界. 具体来说, 存在一个有限常数 κ > 0 \kappa>0 κ>0, 以下条件成立:
sup x ∈ X K ( x , x ) ≤ κ 2 . \sup _{x \in \mathcal{X}} \mathscr{K}(x, x) \leq \kappa^2. x∈XsupK(x,x)≤κ2.
值得注意的是, 任何在紧致域上连续的核函数自然满足上述条件. 此外, 在实践中广泛使用的许多核,例如高斯核和拉普拉斯核, 都在各自的定义域上满足此条件.
2. 对有界似然比的分析
2.1 无权核岭回归接近最优
在这一节中, 首先推导出在协变量转移下的核岭回归估计函数的一系列上界. 结合之后的分析, 这些界限将证实对于具有有界似然比的协变量转移, KRR估计是仅相差对数项的最小最大优的.
定理1 考虑一个均匀 B B B-有界的似然比, 在一个 κ \kappa κ-均匀有界核的希尔伯特空间上的协变量转移回归问题. 那么, 对于任意的 λ ≥ 10 κ 2 / n \lambda \geq 10 \kappa^2 / n λ≥10κ2/n, 核岭回归估计 f ^ λ \widehat{f}_\lambda f λ 满足以下界限
∥ f λ ^ − f ⋆ ∥ Q 2 ≤ 4 λ B ∥ f ⋆ ∥ H 2 ⏟ b λ 2 ( B ) + 80 σ 2 B log n n ∑ j = 1 ∞ μ j μ j + λ B ⏟ v λ ( B ) , \|\widehat{f_\lambda}-f^{\star}\|_Q^2 \leq \underbrace{4 \lambda B\left\|f^{\star}\right\|_{\mathcal{H}}^2}_{\mathbf{b}_\lambda^2(B)}+\underbrace{80 \sigma^2 B \frac{\log n}{n} \sum_{j=1}^{\infty} \frac{\mu_j}{\mu_j+\lambda B}}_{\mathbf{v}_\lambda(B)}, ∥fλ −f⋆∥Q2≤bλ2(B) 4λB∥f⋆∥H2+vλ(B) 80σ2Bnlognj=1∑∞μj+λBμj,
概率至少为 1 − 28 κ 2 λ e − n λ 16 κ 2 − n − 10 . 1 - 28 \frac{\kappa^2}{\lambda} e^{-\frac{n \lambda}{16 \kappa^2}} - n^{-10}. 1−28λκ2e−16κ2nλ−n−10.
该上界主要包含两项. 首项 b λ 2 ( B ) \mathbf{b}_{\lambda}^2(B) bλ2(B)描述了KRR估计的平方偏差, 此偏差随着正则化参数 λ \lambda λ和似然比界 B B B的增加而成比例增长. 其次, v λ ( B ) \mathbf{v}_{\lambda}(B) vλ(B)刻画了KRR估计器的估计方差, 它在 λ \lambda λ的增长下呈现减小的趋势, 从而暗示 λ \lambda λ在调控偏差与方差之间的平衡中起到了核心作用.
接下来进一步分析导致最优 λ ∗ ( B ) \lambda^{*}(B) λ∗(B)的平衡过程. 对于具有规则特征值的核, 这一过程可以更容易地理解. 对于给定的目标误差 δ > 0 \delta>0 δ>0, 考虑描述第一个低于 δ 2 \delta^2 δ2的特征值的指标 d ( δ ) d(\delta) d(δ), 即 d ( δ ) : = min { j ≥ 1 ∣ μ j ≤ δ 2 } d(\delta) := \min\{j\geq1 | \mu_j\leq\delta^2\} d(δ):=min{j≥1∣μj≤δ2}. 特征值序列被称为正则的,如果
∑ j = d ( δ ) + 1 ∞ μ j ≤ c d ( δ ) δ 2 , \sum_{j=d(\delta)+1}^{\infty} \mu_j \leq c d(\delta) \delta^2, j=d(δ)+1∑∞μj≤cd(δ)δ2,
对某常数 c c c成立. 正则特征值核的包括有限秩核以及特征值在多项式或指数层面上呈现逐渐衰减的核, 这些核广泛应用于实际中. 对于带有正则特征值的核函数, 我们可以证明存在常数 c ′ c' c′使得
∥ f ^ λ − f ⋆ ∥ Q 2 ≤ c ′ { δ 2 ∥ f ⋆ ∥ H 2 + σ 2 B d ( δ ) log n n } , δ 2 = λ B . \|\widehat{f}_\lambda - f^{\star}\|_Q^2 \leq c^{\prime}\left\{\delta^2\left\|f^{\star}\right\|_{\mathcal{H}}^2 + \sigma^2 B \frac{d(\delta) \log n}{n}\right\}, ~~ \delta^2 = \lambda B. ∥f λ−f⋆∥Q2≤c′{δ2∥f⋆∥H2+σ2Bnd(δ)logn}, δ2=λB.
2.2 带有协变量偏移的正则核的下界
上一节我们为非加权的KRR估计建立了上界. 这一节我们证明对于具有正则特征值的核, 非加权KRR估计函数所实现的界是极小极大最优的.
定理2 对于任意的 B ≥ 1 B\geq1 B≥1, 存在一对似然比为 B B B-有界的分布 ( P , Q ) (P, Q) (P,Q), 以及在 L 2 ( Q ) L^2(Q) L2(Q)中的一组正交基 { ϕ j } j ≥ 1 \{\phi_j\}_{j \geq 1} {ϕj}j≥1 使得对于任意的正则核特征值序列 使得对于任意的正则核特征值序列 使得对于任意的正则核特征值序列 { μ j } j ≥ 1 \{\mu_j\}_{j \geq 1} {μj}j≥1, 有
inf f ^ sup f ⋆ ∈ B H ( 1 ) E [ ∥ f ^ − f ⋆ ∥ Q 2 ] ≥ c inf δ > 0 { δ 2 + σ 2 B d ( δ ) n } . \inf _{\widehat{f}} \sup _{f^{\star} \in \mathcal{B}_{\mathcal{H}}(1)} \mathbb{E}[\|\widehat{f}-f^{\star}\|_Q^2] \geq c \inf _{\delta>0}\left\{\delta^2+\sigma^2 B \frac{d(\delta)}{n}\right\}. f inff⋆∈BH(1)supE[∥f −f⋆∥Q2]≥cδ>0inf{δ2+σ2Bnd(δ)}.
与2.1节末的结果相比, 我们观察到当选择合适的正则化参数 λ \lambda λ时, KRR 估计函数实现了极小极大最优 (仅相差对数项).
3. 对无界似然比的分析
到目前为止,我们的分析都基于 B B B-有界的似然比. 但实际上似然比往往是无界的. 以一个简单的单变量例子为证,假设目标分布 Q Q Q是标准正态分布 N ( 0 , 1 ) \mathcal{N}(0,1) N(0,1), 而源分布 P P P为 N ( 0 , 0.9 ) \mathcal{N}(0,0.9) N(0,0.9). 不难发现, 随着 ∣ x ∣ |x| ∣x∣趋于无穷,似然比 ρ ( x ) \rho(x) ρ(x)也趋于无穷。在1.2节中我们提到,用似然加权估计器的一个担忧是它们可能导致方差的大幅膨胀, 特别是乘以可能无界的似然比 ρ ( x ) \rho(x) ρ(x). 因此, 我们考虑将 ρ ( x ) \rho(x) ρ(x)截断: 更具体地说, 对于给定的 τ n > 0 \tau_{n}>0 τn>0, 我们定义截断后的似然比为
ρ τ n ( x ) : = { ρ ( x ) if ρ ( x ) ≤ τ n τ n otherwise \rho_{\tau_n}(x) := \begin{cases}\rho(x) & \text { if } \rho(x) \leq \tau_n \\ \tau_n & \text { otherwise }\end{cases} ρτn(x):={ρ(x)τn if ρ(x)≤τn otherwise
并定义截断加权KRR估计函数:
f ^ λ r w : = arg min f ∈ H { 1 n ∑ i = 1 n ρ τ n ( x i ) ( f ( x i ) − y i ) 2 + λ ∥ f ∥ H 2 } , \widehat{f}_\lambda^{\mathrm{rw}}:=\arg \min _{f \in \mathcal{H}}\left\{\frac{1}{n} \sum_{i=1}^n \rho_{\tau_n}\left(x_i\right)\left(f\left(x_i\right)-y_i\right)^2+\lambda\|f\|_{\mathcal{H}}^2\right\}, f λrw:=argf∈Hmin{n1i=1∑nρτn(xi)(f(xi)−yi)2+λ∥f∥H2},
其中 λ > 0 \lambda>0 λ>0和 τ n \tau_n τn待定.
在核的特征函数均匀有界时, 我们对估计函数进行了分析. 核特征函数均匀有界指
∥ ϕ j ∥ ∞ : = sup x ∈ X ∣ ϕ j ( x ) ∣ ≤ 1 ∀ j = 1 , 2 , … \left\|\phi_j\right\|_{\infty}:=\sup _{x \in \mathcal{X}}\left|\phi_j(x)\right| \leq 1 \quad \forall j=1,2, \ldots ∥ϕj∥∞:=x∈Xsup∣ϕj(x)∣≤1∀j=1,2,…
关于截断加权KRR估计函数的定理涉及核复杂性函数 Ψ ( δ , μ ) = ∑ j = 1 ∞ min { δ 2 , μ j ∥ f ⋆ ∥ H 2 } \Psi(\delta, \mu)=\sum_{j=1}^{\infty} \min \left\{\delta^2, \mu_j\left\|f^{\star}\right\|_{\mathcal{H}}^2\right\} Ψ(δ,μ)=∑j=1∞min{δ2,μj∥f⋆∥H2}, 并适用于任意满足不等式 M ( δ ) < δ 2 2 \mathcal{M}(\delta)<\frac{\delta^2}{2} M(δ)<2δ2 的解 δ n > 0 \delta_n>0 δn>0, 其中:
M ( δ ) : = c 0 σ 2 V 2 log 3 ( n ) n Ψ ( δ , μ ) . \mathcal{M}(\delta):=c_0 \sqrt{\frac{\sigma^2 V^2 \log ^3(n)}{n} \Psi(\delta, \mu)} . M(δ):=c0nσ2V2log3(n)Ψ(δ,μ).
定理3 考虑均匀有界的特征函数的核, 以及满足 E P [ ρ ( x ) 2 ] ≤ V 2 \mathbb{E}_{P}[\rho(x)^2]\leq V^2 EP[ρ(x)2]≤V2的源-目标分布. 进一步假设噪声的方差满足 σ 2 ≤ κ 2 ∥ f ⋆ ∥ H 2 \sigma^2\leq\kappa^2\|f^{\star}\|_{\mathcal{H}}^2 σ2≤κ2∥f⋆∥H2. 那么, 有截断阈值 τ n = n V 2 \tau_n=\sqrt{nV^2} τn=nV2 和正则化参数 λ ∥ f ⋆ ∥ H 2 ≥ δ n 2 / 3 \lambda\left\|f^{\star}\right\|_{\mathcal{H}}^2\geq\delta_n^2 / 3 λ∥f⋆∥H2≥δn2/3的估计函数 f ^ λ r w \hat{f}_{\lambda}^{rw} f^λrw 有上界:
∥ f ^ λ r w − f ⋆ ∥ Q 2 ≤ δ n 2 + 3 λ ∥ f ⋆ ∥ H 2 , \|\hat{f}_\lambda^{\mathrm{rw}}-f^{\star}\|_Q^2 \leq \delta_n^2+3 \lambda\left\|f^{\star}\right\|_{\mathcal{H}}^2, ∥f^λrw−f⋆∥Q2≤δn2+3λ∥f⋆∥H2,
其概率为 1 − n − 10 1-n^{-10} 1−n−10.
参考文献
[1] Cong Ma, Reese Pathak, Martin J. Wainwright “Optimally tackling covariate shift in RKHS-based nonparametric regression,” The Annals of Statistics, Ann. Statist. 51(2), 738-761, (April 2023)
相关文章:

优化|优化处理可再生希尔伯特核空间的非参数回归中的协变量偏移
原文:Optimally tackling covariate shift in RKHS-based nonparametric regression. The Annals of Statistics, 51(2), pp.738-761, 2023. 原文作者:Cong Ma, Reese Pathak, Martin J. Wainwright 论文解读者:赵进 编者按: …...

Netty深入浅出Java网络编程学习笔记(一) Netty入门篇
目录 一、概述 1、什么是Netty 2、Netty的优势 二、入门案例 1、服务器端代码 2、客户端代码 3、运行流程 组件解释 三、组件 1、EventLoop 处理普通与定时任务 关闭 EventLoopGroup 处理IO任务 服务器代码 客户端代码 分工细化 划分Boss 和Work 增加自定义EventLoopGroup 切换…...
自动化产线集控系统(西门子CNC 840D/840DSL远程控制)
1.1项目背景 RQQ/VF120机组目前为1人操作3台机床,需在机台旁监控。为了改善人员在班中劳动强度非常大的现状,调整好每台机床的节奏,以保证机床的最少的等待时间。本项目旨在通过远程监视设备运行过程关键参数,操作人员人员可远程监…...
MVVM 与 MVC区别和应用场景?
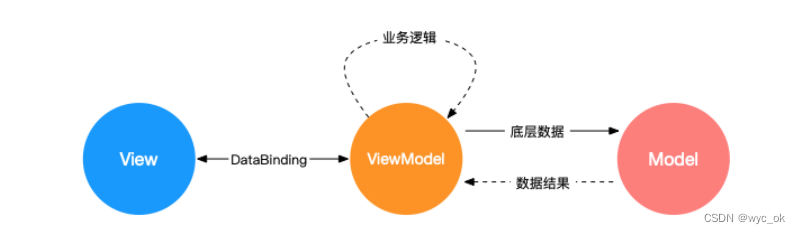
MVVM 和 MVC 1. MVC2. MVVM 1. MVC MVC 是 Model View Controller 的缩写 Model:模型层,是应用程序中用于处理应用程序数据逻辑的部分。通常模型对象负责在数据库中存取数据。View:视图层,用户界面渲染逻辑,通常视图…...

Linux开发-Ubuntu软件源工具
开发&验证环境: 操作系统:ubuntu 20.04 软件源:http://archive.ubuntu.com/ubuntu 开发工具 sudo apt install vim sudo apt install git# gnu工具链 sudo apt install gcc sudo apt install g sudo apt install gdb# llvm工具链 sudo …...
环境下载地址
1. DOTNET环境下载 适用于 Visual Studio 的 .NET SDK 下载 (microsoft.com)https://dotnet.microsoft.com/zh-cn/download/visual-studio-sdks...
)
E. Block Sequence-Codeforces Round 903 (Div. 3)
E. Block Sequence dp题,设dp[i]表示i~n之间的数,需要最小删除数量 那么每一位数有两种情况,设数a[i]: 1.被删除:dp[i]dp[i1]1,这一位等于上一位的加一。 2.被保留:dp[i]min(dp[i],dp[ia[i]1]); #include<iostream…...
路由router
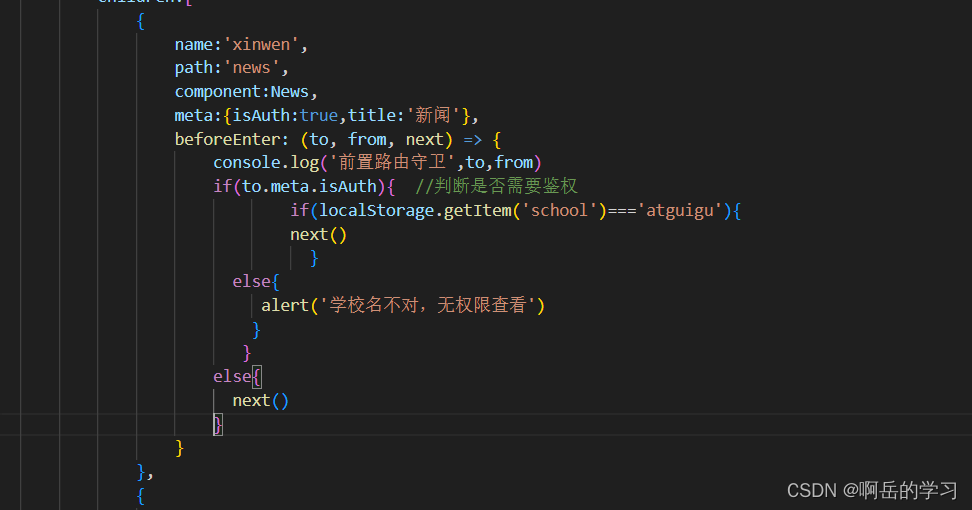
什么是路由? 一个路由就是一组映射关系(key - value)key 为路径,value 可能是 function 或 component 2、安装\引入\基础使用 只有vue-router3,才能应用于vue2;vue-router4可以应用于vue3中 这里我们安装vue-router3…...

学习编程-先改变心态
编程失败的天才 林一和我很久以前就认识了——我从五年级就认识他了。他是班上最聪明的孩子。如果每个人在家庭作业或考试准备方面需要帮助,他们都会去那里。 有趣的是,林一不是那种连续学习几个小时的孩子。 他的聪明才智似乎与生俱来,几乎毫…...

【Node.js】http 模块
1. http 模块 import http from http // 创建本地服务器接收数据 const server http.createServer((req, res) > {console.log(req.url)res.writeHead(200, { Content-Type: application/json // Content-Type: text/html;charsetutf-8 // 将内容以 html 标签和 utf-8 的…...
S/4 HANA 大白话 - 财务会计-2 总账主数据
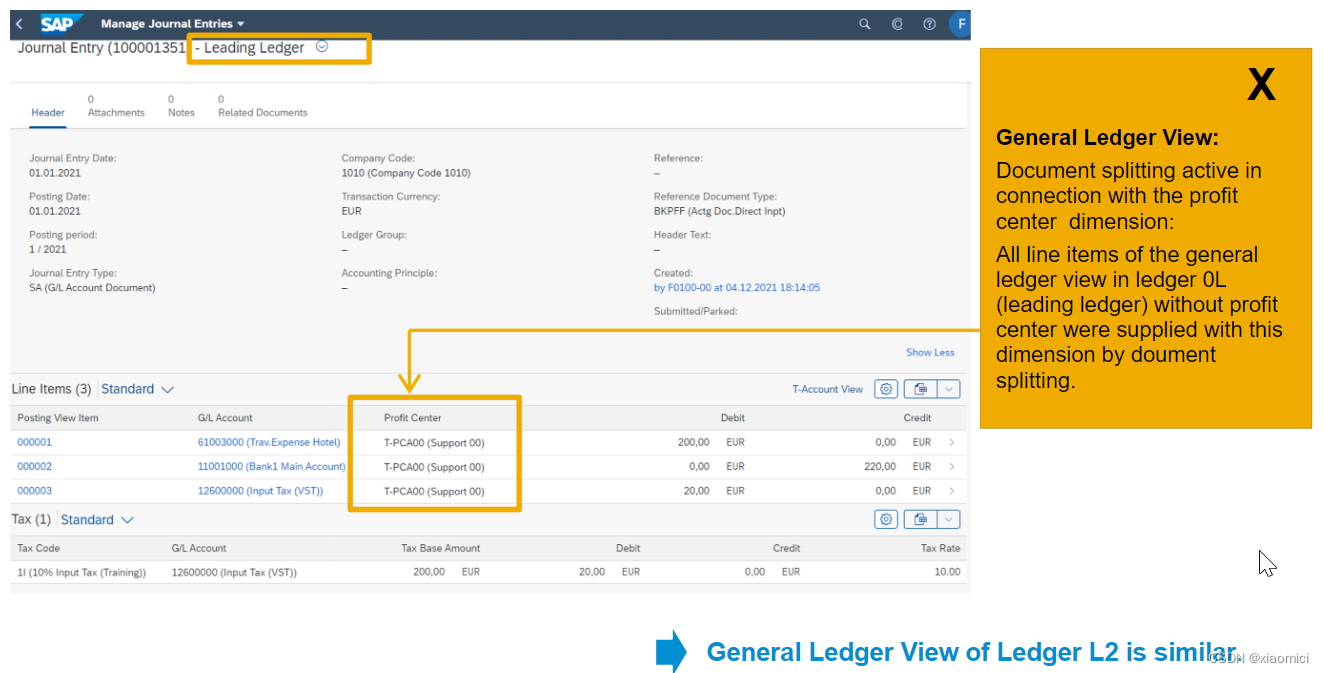
接下来看看财务模块的一些具体操作。 总账相关主数据 公司每天运转,每天办公室有租金,有水电费,有桌椅板凳损坏,鼠标损坏要换,有产品买卖,有收入。那么所有这些都得记下来。记哪里?记在总账里…...
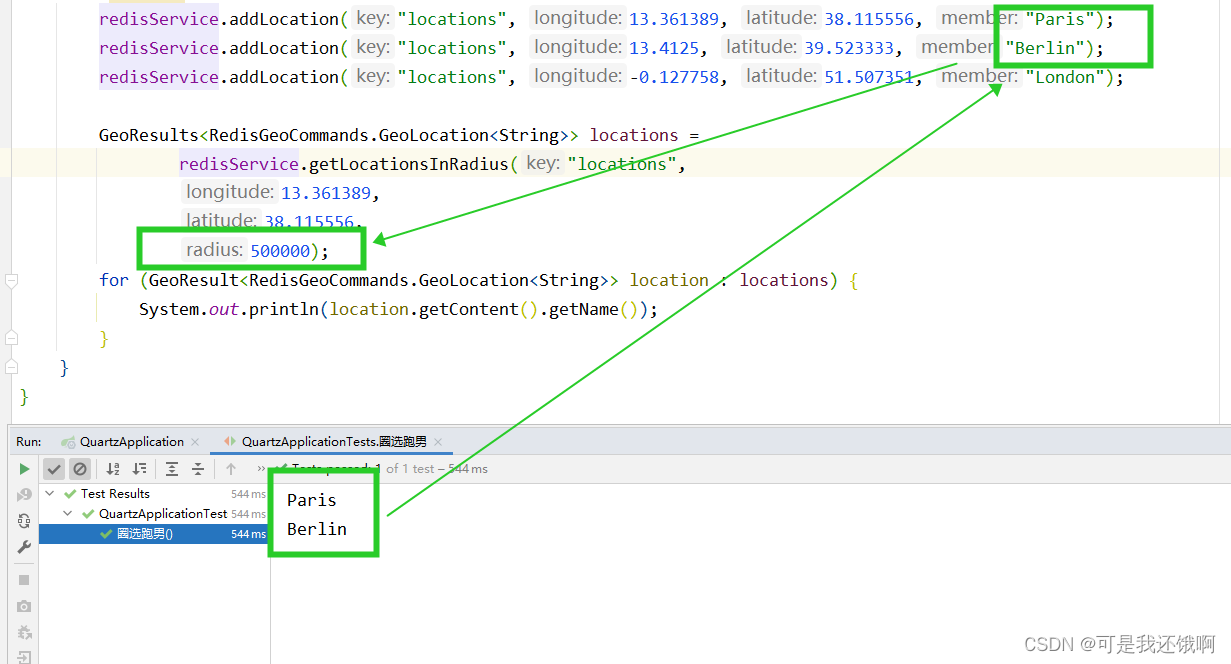
Redis根据中心点坐标和半径筛选符合的数据
目录 1.启动Redis编辑 2.导入maven依赖 3.添加redis配置 4.编写RedisService 5.使用 6.验证 1.启动Redis 2.导入maven依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifac…...

springboot 集成 zookeeper 问题记录
springboot 集成 zookeeper 问题记录 环境 springboot - 2.7.8 dubbo - 3.1.11 dubbo-dependencies-zookeeper-curator5 - 3.1.11 模拟真实环境,将 windows 上的 zookeeper 迁移到虚拟机 linux 的 docker 环境 failed to connect to zookeeper server 迁移到…...
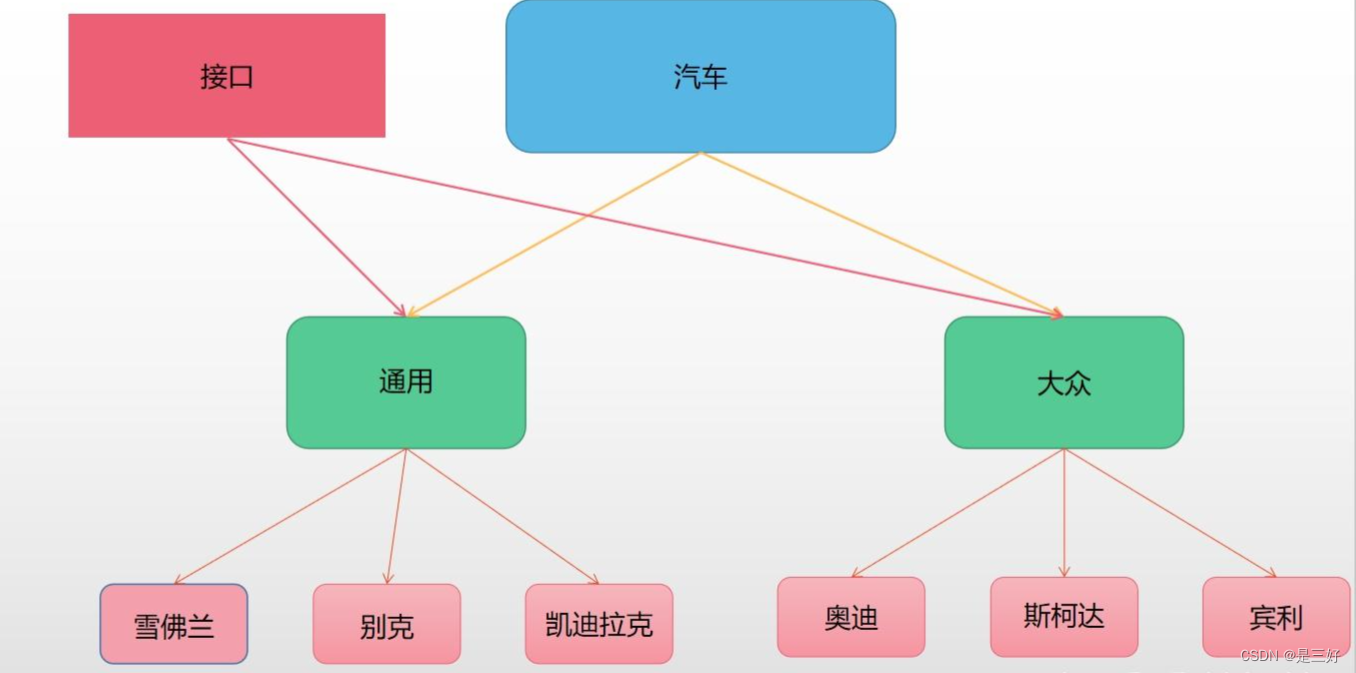
java中的接口interface
一、面向对象基本概念 Java是一种面向对象的语言,其中「对象」就相当于是现实世界中的一个个具体的例子,而「类」就相当于是一个抽象的模板,将抽象的概念模板转化为具体的例子的过程就叫做「实例化」。 比如说人这个概念就是一个抽象化的「…...

多个git提交,只推送其中一个到远程该如何处理
用新分支去拉取当前分支的指定commit记录,之后推送到当前分支远程仓库实现推送指定历史提交的功能 1.查看当前分支最近五次提交日志 git log --oneline -5 2.拉取远程分支创建临时本地分支 localbranch 为本地分支名 origin/dev 为远程目标分支 git checkout …...

uniapp中input的disabled属性
uniapp中input的disabled属性: 小程序中兼容性好; 在H5中兼容性差; 在H5中使用uniapp的input的disabled属性,属性值只能是true或false,如果为0, "都会为true; <input class"in…...
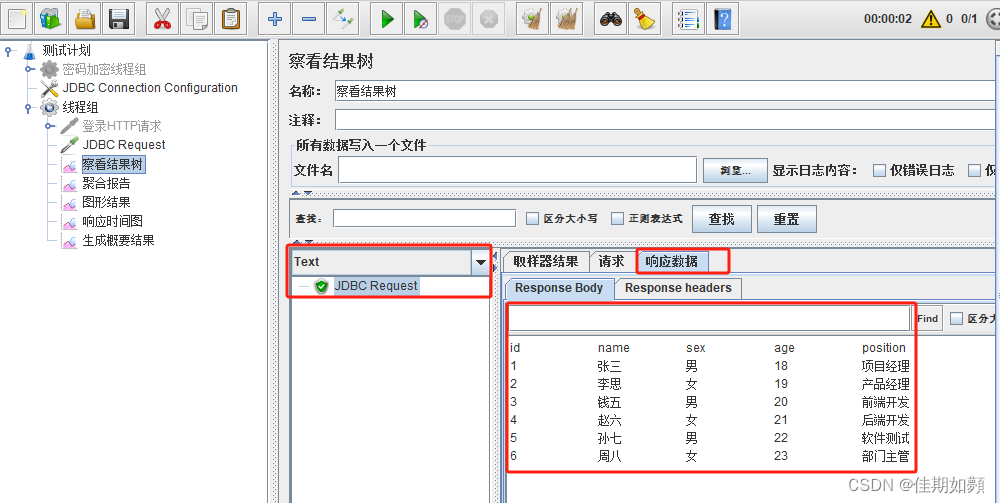
Jmeter连接mysql数据库详细步骤
一、一般平常工作中使用jmeter 连接数据库的作用 主要包括: 1、本身对数据库进行测试(功能、性能测试)时会需要使用jmeter连接数据库 2、功能测试时,测试出来的结果需要和数据库中的数据进行对比是否正确一致。这时候可以通过j…...
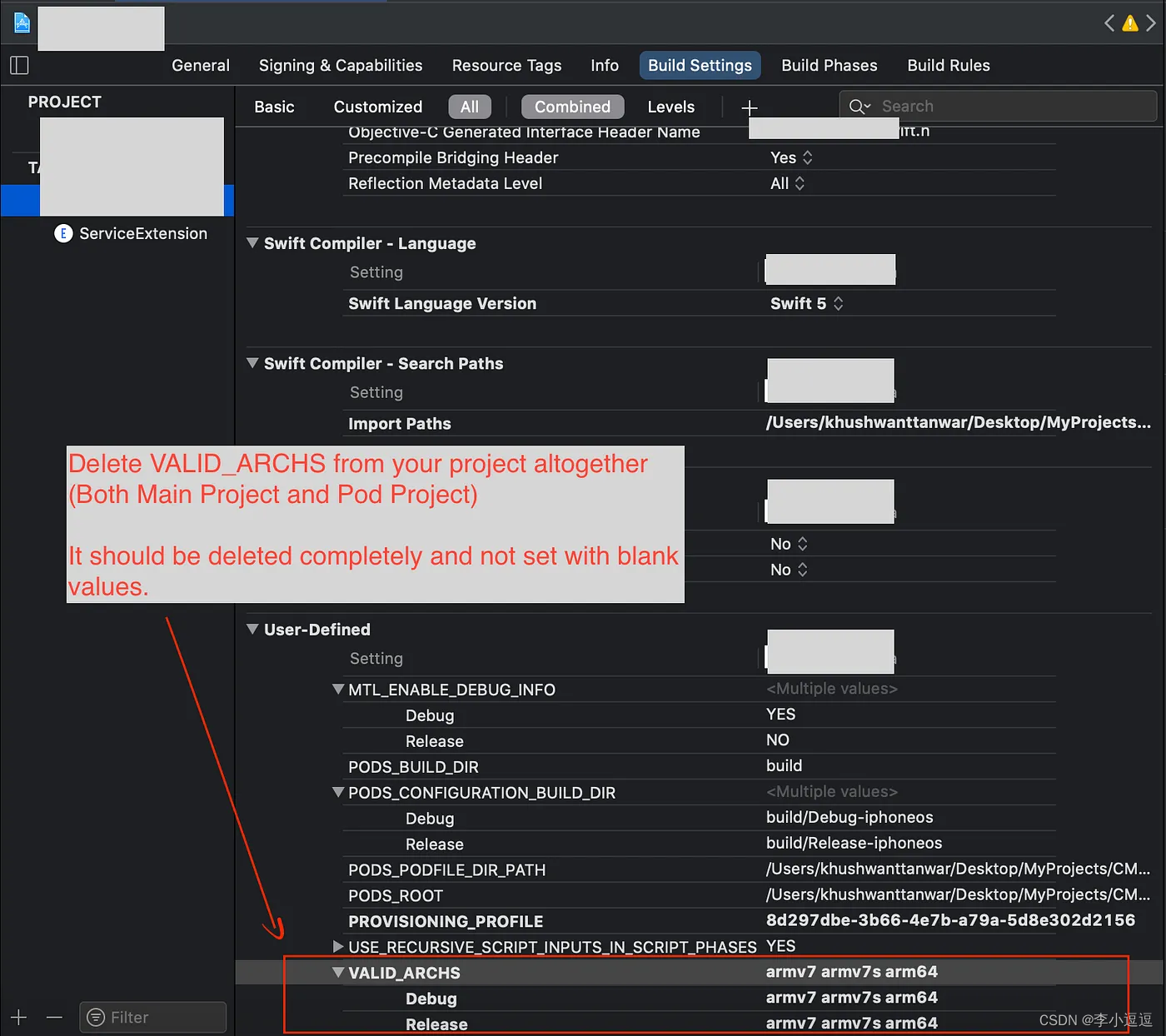
Xcode 14.3.1build 报错整理
1、Command PhaseScriptExecution failed with a nonzero exit code 2、In /Users/XX/XX/XX/fayuan-mediator-app-rn/ios/Pods/CocoaLibEvent/lib/libevent.a(buffer.o), building for iOS Simulator, but linking in object file built for iOS, file /Users/XX/XX/XX/fayuan…...

TensorFlow入门(十三、动态图Eager)
一个图(Graph)代表一个计算任务,且在模型运行时,需要把图放入会话(session)里被启动。一旦模型开始运行,图就无法修改了。TensorFlow把这种图一般称为静态图。 动态图是指在Python中代码被调用后,其操作立即被执行的计算。 它与静态图最大的区别是不需要使用session来建立会话…...
批量执行insert into 的脚本报2006 - MySQL server has gone away
数据库执行批量数据导入是报“2006 - MySQL server has gone away”错误,脚本并没有问题,只是insert into 的批量操作语句过长导致。 解决办法: Navicat ->工具 ->服务器监控->mysql ——》变量 修改max_allowed_packet大小为512…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
